數形結合方法在高中數學教學中的應用探究

王菊

數學在各個科學中的地位都十分重要，不僅是由于數學是刻畫自然規律與社會規律的重要語言工具，更是由于數學科學的科學性與有效性所決定的，也正是因此，數學有著“科學之母”的美譽。數學在高中階段是研究空間關系與數量關系的科學，這就決定了數形結合教學法在高中數學教學中廣泛運用的理論基礎。數形結合法在形式上有助于學生將抽象概括的數學知識與具象的數學圖形有機結合在一起，是極為有效的數學學習方式，在高中數學教學過程中，不僅可以使學生進行基礎數學知識的構建，還可以加強學生數學能力的培養和數學思想方法的應用。

一、數形結合方法在三角函數定義教學中的應用

在高中數學教學與學習中，有著許許多多的知識點，在這中間“數量關系”、“空間形式”、“數形結合”等是高中數學重點的學習思維方式，在數形結合思想中，高中學生第一個接觸的就是三角函數，三角函數不僅僅是函數知識，更是描述周期性的數學模型，從定義上就可以看出三角函數是數形結合思想的產物。如果學生僅依靠代數知識對三角函數進行計算，不僅加大了學生的運算量，還違背了數學計算的簡要性原則。假使學生僅依靠圖形知識對三角函數進行求導，由于缺乏邏輯與數值進行約束，學生也無法得出三角函數的周期性。因此教師在對學生進行三角函數知識點教學時，就應當為學生引入數形結合法為學生提供思想學習方案，提高學生的數學學習效率、例如：求三分之五π的正弦、余弦和正切值。多數情況下學生僅能依靠已學得的兩種定義進行求解，但通過定義法進行學習不利于學生快速求解，當學生計算能力較差時更是容易出錯。當采用數形結合法進行學習時可以快速求解，其邏輯過程是這樣的：在直角坐標系中在角五分 [y][x][o][A][P（1，y）][圖3-1] 之三π上任取點P，畫輔助線AP，得到一個三角形Rt△PAO（圖3-1所示），通過各點的坐標得出各線段的長度，再根據定義1求解。這就是數形結合法在三角函數中的應用示例。

二、數形結合方法在直線與圓錐曲線教學中的應用

直線與圓錐曲線在高中教學范圍內同屬于解析幾何的知識范疇，同屬于近代數學的基礎。在這一知識點的學習過程中學生明顯會感到不適應，因為在初中階段的幾何問題學習中，幾何問題是常量問題并不牽扯變量，但在高中階段這一情況就發生了巨大變化，幾何數學問題中開始充斥著變量給學生帶來了巨大的運算量變化的同時也帶來的學習困難。而通常數學教師在這一章節中教師最常用的教學法就是“坐標法”，而坐標法所代表的內涵即是數形結合思想。例如：判斷直線AB和PQ的位置關系（ ）。A（2，3）B（-1，0）P（1，0）Q（0，-1）在這一問題中學生可以通過方程進行計算，但這樣會給學生帶來 [y][x][A][B][o][Q][P][2][-1][-1][3][圖3-10] 較大的運算量，給學生帶來麻煩，而當學生采用數形結合思想的坐標法時，可以進行定點作圖（如圖3-10所示）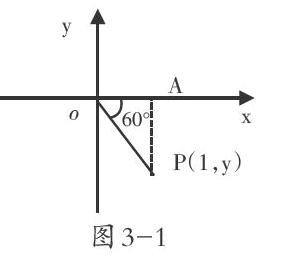

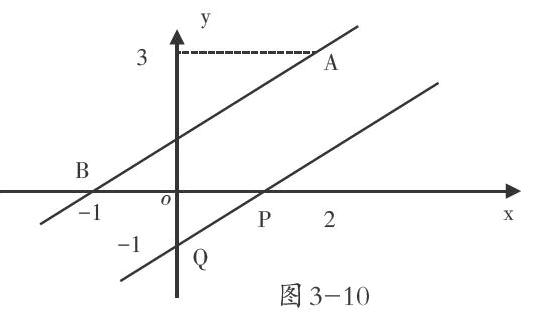
這樣的優勢在于圖形可以繪畫的簡單明了并便于驗證，這種思想及方式不僅為學生帶來了便利性的問題解決方式，更是帶來了新的問題解決角度。

三、數形結合方法在向量教學中的應用

向量知識在高中知識范圍內所涉及的知識點不多也并不復雜，但由于高考試卷中是常考問題其重要性不言而喻。向量知識的起源在于物理學的矢量，這種數字變量的特性在于既有大小又有方向，學生在進行學習時往往無法了解到這一點，經常會在向量的方向學習上出錯。這是由于學生是將原有的代數解題法套用到了向量問題中，但由于代數解題法在這種具有多重屬性問題中的先天劣勢，往往會使學生感到手足無措。當教師采用數形結合法進行向量問題的教學時就會有利于學生對向量問題的理解，從而將向量中的代數關系與幾何關系緊密聯系起來。在這樣的關系結構中不僅可以將向量中的數量關系圖形化，更可以將圖形數量化，從而打通其二者間的聯系。

四、結語

數形結合思想不僅有利于學生解決數學中的幾何、代數問題，更有利于幫助學生將二者進行有機聯系及轉化。學生在初中數學學習中學習的知識多數是直觀的具象問題，而高中數學問題多數是抽象化的理念運用問題，當學生可以嫻熟運用數形結合方法到數學問題解決中，就可以很輕松地在初中數學與高中數學知識中構建過渡銜接的橋梁。作為教師應當充分發揮數形結合法在數學教學中的優勢作用，促進學生數學學習成績的提高。endprint