一種數(shù)字磁羅盤全羅差自主優(yōu)化補(bǔ)償方法

洪琪璐,張愛軍*,王昌明

(南京理工大學(xué)機(jī)械工程學(xué)院,南京 210094)

一種數(shù)字磁羅盤全羅差自主優(yōu)化補(bǔ)償方法

洪琪璐1,張愛軍1*,王昌明2

(南京理工大學(xué)機(jī)械工程學(xué)院,南京 210094)

為了進(jìn)一步提高數(shù)字磁羅盤全姿態(tài)羅差補(bǔ)償精度,提出了一種基于地磁場(chǎng)分量的羅差自主優(yōu)化補(bǔ)償方法。從羅差補(bǔ)償模型出發(fā),分析橢球擬合補(bǔ)償方法的局限性,在對(duì)參數(shù)缺失和剩余誤差分析的基礎(chǔ)上,建立了包含缺失參數(shù)的優(yōu)化補(bǔ)償模型;針對(duì)非線性優(yōu)化模型引入粒子群算法PSO(Particle Swarm Optimization)對(duì)模型參數(shù)進(jìn)行估計(jì),數(shù)值仿真結(jié)果證明了算法可有效估計(jì)缺失參數(shù)。實(shí)驗(yàn)結(jié)果表明,優(yōu)化補(bǔ)償過程無需借助外部輔助姿態(tài)信息,俯仰角-20°姿態(tài)下,優(yōu)化補(bǔ)償方法在橢球假設(shè)補(bǔ)償基礎(chǔ)上將其最大誤差由4.8°降至1.9°,誤差標(biāo)準(zhǔn)差由1.5°降至1.1°。

數(shù)字磁羅盤;全羅差;非線性;粒子群算法

數(shù)字磁羅盤是一種利用地球磁場(chǎng)與重力加速度實(shí)現(xiàn)航向測(cè)量的工具,由于其捷聯(lián)特性和體積、精度等方面的優(yōu)勢(shì)已被廣泛應(yīng)用于導(dǎo)航定位系統(tǒng)中。在實(shí)際應(yīng)用中,磁羅盤極易受到載體周邊雜散磁場(chǎng)地干擾,造成較大的磁航向測(cè)量誤差(羅差),為實(shí)現(xiàn)高精度、高可靠性的導(dǎo)航與定位,必須對(duì)磁羅盤羅差進(jìn)行有效的校正。在眾多的羅差補(bǔ)償方法中,Moulin M等[1]提出的羅差橢球假設(shè)補(bǔ)償方法具備的全姿態(tài)范圍羅差的補(bǔ)償能力,且無需依賴外部輔助姿態(tài)信息、自主補(bǔ)償能力較強(qiáng),在實(shí)際工程中被廣泛應(yīng)用并得到國(guó)內(nèi)外學(xué)者進(jìn)一步的深入研究。文獻(xiàn)[2-3]基于泊松模型,分析橢球假設(shè)理論的正確性,采用最小二乘橢球擬合算法求取模型參數(shù),計(jì)算量小。文獻(xiàn)[4]提出了帶約束的最小二擬合算法,保證擬合橢球算法的穩(wěn)定性。但文獻(xiàn)[2]指出橢球假設(shè)方法存在辨識(shí)參數(shù)缺失的問題,橢球假設(shè)可以很好地辨識(shí)出硬磁干擾系數(shù),但對(duì)軟磁干擾系數(shù)矩陣非對(duì)角元素的辨識(shí)能力不足,剩余的非對(duì)準(zhǔn)誤差造成了較強(qiáng)非線性的羅差。文獻(xiàn)[5]也證明了橢球假設(shè)存在軟磁干擾系數(shù)矩陣非對(duì)角元素存在相互耦合的問題,而采用橢球假設(shè)方法對(duì)非對(duì)準(zhǔn)誤差是不可觀測(cè)的,需要進(jìn)一步設(shè)計(jì)優(yōu)化方法補(bǔ)償非對(duì)準(zhǔn)誤差。雖然文獻(xiàn)[6-8]提出的十二位置標(biāo)定法、遞推最小二乘法、最大似然估計(jì)法、遺傳算法均可實(shí)現(xiàn)對(duì)非對(duì)準(zhǔn)誤差的補(bǔ)償,但需要重新借助外部輔助姿態(tài)信息,原有橢球假設(shè)方法的自主補(bǔ)償優(yōu)勢(shì)不再。非對(duì)準(zhǔn)誤差可以看為安裝誤差的一種來進(jìn)行補(bǔ)償[9]。文獻(xiàn)[10]借助外部平面的約束對(duì)安裝誤差進(jìn)行補(bǔ)償,但需要多次使用最小二乘法提高擬合精度,過程繁瑣。

在前人工作的基礎(chǔ)上,本文提出了一種融合磁羅盤自身姿態(tài)信息的自主優(yōu)化補(bǔ)償方法。在橢球假設(shè)補(bǔ)償?shù)幕A(chǔ)上,方法僅利用磁羅盤自身輸出的信息一步估計(jì)出剩余缺失參數(shù)并對(duì)非對(duì)準(zhǔn)誤差進(jìn)行修正,從而進(jìn)一步實(shí)現(xiàn)羅差優(yōu)化補(bǔ)償,同時(shí)整個(gè)優(yōu)化補(bǔ)償過程無需借助外部姿態(tài)信息。仿真實(shí)驗(yàn)與實(shí)物實(shí)驗(yàn)的結(jié)果均證明了本文提出優(yōu)化方法的正確性和有效性。

1 羅差模型與補(bǔ)償分析

1.1 羅差模型

定義Hb=[Hbx,Hby,Hbz]T為地球磁場(chǎng)在載體坐標(biāo)系下的分量,Hm=[Hmx,Hmy,Hmz]T為三軸地磁傳感器實(shí)際測(cè)量值。地磁傳感器受到載體鐵磁物體影響,其敏感的磁場(chǎng)強(qiáng)度為地磁場(chǎng)與載體雜散干擾磁場(chǎng)疊加的總和,根據(jù)矢量疊加原理:

Hm=Hb+KHb+ξ

(1)

令A(yù)=K+I3×3,變換式(1)可得:

Hb=A-1(Hm-ξ)

(2)

式即為地磁傳感器的誤差補(bǔ)償模型,若能確定A-1,ξ,就能由地磁傳感器測(cè)量值計(jì)算地磁場(chǎng)強(qiáng)度在載體坐標(biāo)系上的分量,由式(3)、式(4)計(jì)算出真實(shí)的磁航向ψ。

Ht=R(θ,γ)Hb

(3)

ψ=arctan(Hty/Htx)

(4)

式中:Ht為Hb在當(dāng)?shù)厮阶鴺?biāo)系中的投影,θ、γ為磁羅盤輸出俯仰角與橫滾角,R(θ,γ)為對(duì)應(yīng)的旋轉(zhuǎn)矩陣。

1.2 羅差模型

在固定的空間位置,地磁場(chǎng)矢量的模的長(zhǎng)短不變時(shí),根據(jù)式(2)可得:

(5)

式中:L=(A-1)TA-1。式(5)表示了一個(gè)有關(guān)自變量Hm的橢球方程,表明Hm測(cè)量值軌跡為一橢球。采集多組測(cè)量值,通過最小二乘擬合等方法確定橢球方程解出L與ξ。矩陣A-1進(jìn)一步由L求出,此后通過由式(2)即可完成羅差補(bǔ)償。

A-1可通過分解正定矩陣L來確定。目前對(duì)于矩陣L分解方法,有Cholesky分解、極分解、奇異值分解等[2,4],但各類分解方法得出的矩陣A-1并不一致。針對(duì)上述情況進(jìn)行分析,假定存在一個(gè)任意的正交矩陣Q,使得R=QA-1,則有:

RTR=(A-1)TQA-1=(A-1)TQTA-1=(A-1)TA-1=L

(6)

由式(6)可見,各種分解方法得出的矩陣之間必會(huì)相差一個(gè)正交矩陣。幾何意義上,正交矩陣Q的存在相當(dāng)于將補(bǔ)償后地磁場(chǎng)測(cè)量軸系相對(duì)于較重力加速度測(cè)量軸系旋轉(zhuǎn)了一定角度,引入了軸系間的非對(duì)準(zhǔn)誤差。文獻(xiàn)[2]中實(shí)驗(yàn)證明了非對(duì)準(zhǔn)誤差的存在會(huì)造成較強(qiáng)的非線性羅差。

(7)

2 優(yōu)化補(bǔ)償方法設(shè)計(jì)

由前文分析可知,進(jìn)一步優(yōu)化羅差補(bǔ)償精度的重點(diǎn)在于確定正交矩陣Q。固定空間位置,地磁場(chǎng)矢量的模長(zhǎng)與方向均不變,因此其豎直分矢量與水平分矢量均為常矢量,如圖1所示。以地磁場(chǎng)強(qiáng)度豎直分矢量Htz為例:

Htz=F(θ,γ)Hb=F(θ,γ)QHs

(8)

式中:Hs=A′-1(Hm-ξ)為橢球假設(shè)補(bǔ)償后的三維地磁數(shù)據(jù),F(θ,γ)=[sinθ,-cosθsinγ,cosθcosγ]T為旋轉(zhuǎn)矩陣R(θ,γ)中第3行行向量。顯然若矩陣Q缺失,式(8)必不成立。因此通過采集多組θ、γ和Hs利用式(8)中Htz固定不變的約束可以確定矩陣Q。根據(jù)空間軸系的旋轉(zhuǎn)關(guān)系,將Q簡(jiǎn)化3參數(shù)的方向余弦矩陣,如式(7)所示。那么式(8)表示為一個(gè)關(guān)于參數(shù)β1、β2、β3的非線性方程,估計(jì)出該參數(shù)方程,即可由式(7)確定誤差矩陣Q,矩陣A-1則唯一確定:A-1=QA′-1,從而完成優(yōu)化補(bǔ)償。

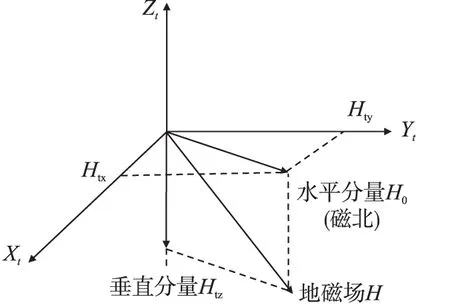
圖1 地磁場(chǎng)在水平坐標(biāo)中投影示意圖

對(duì)于非線性參數(shù)方程,通常通過求導(dǎo)進(jìn)行泰勒級(jí)數(shù)展開將其轉(zhuǎn)化為線性方程,然后應(yīng)用最小二乘法迭代進(jìn)行求解,但算法極易受選取的初值影響而發(fā)散,且實(shí)際工程中初值選取也較為困難。粒子群算法PSO(Particle Swarm Optimization)是一種基于群體智能的優(yōu)化算法,通過種群個(gè)體之間的相互協(xié)作與競(jìng)爭(zhēng),實(shí)現(xiàn)求取最優(yōu)解,和其他算法相比,PSO代碼量小,易于實(shí)現(xiàn),尤其對(duì)初值要求不高,且具備全局收斂性,在實(shí)際工程中被廣泛使用[11]。本文也引入該種方法對(duì)式(7)中參數(shù)進(jìn)行估計(jì),設(shè)計(jì)PSO估計(jì)步驟如下:

①由式(8)構(gòu)造以下函數(shù):

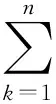
(9)

式中:ζ=(β1,β2,β3)T為待估計(jì)參數(shù)向量,k為測(cè)量序列,n為磁羅盤數(shù)據(jù)采樣點(diǎn)個(gè)數(shù)。L(ζ)越小說明Htzk越接近于真實(shí)地磁場(chǎng)豎直分量Htz,最小時(shí)則認(rèn)為ζ收斂于真值,因此設(shè)計(jì)的目標(biāo)函數(shù)為:

F(ζ)=minL(ζ)

(10)

式(10)表示ζ是在使n個(gè)采樣點(diǎn)Htzk的統(tǒng)計(jì)值L(ζ)最小時(shí)的參數(shù)值。

②滿足βij～U[βmin,βmax],Vij～U[Vmin,Vmax]條件,隨機(jī)給定微粒初始位置βij與初始速度Vij,i=1,2,…,M,j=1,2,3,M為種群大小。初始個(gè)體適應(yīng)度pbesti與全局最優(yōu)適應(yīng)度gbest。

(11)

③更新微粒的速度與位置。

(12)

式中:t為當(dāng)前進(jìn)化代數(shù),r1、r2為均勻分布于(0-1)區(qū)間的隨機(jī)數(shù),ω為慣性權(quán)重,c1、c2為加速因子。

④更新pbesti、gbest,若達(dá)到最大進(jìn)化代數(shù)或滿足精度標(biāo)準(zhǔn),搜索終止;否則執(zhí)行步驟②。

3 仿真驗(yàn)證與分析

為了驗(yàn)證方法的有效性與正確性,采用仿真數(shù)據(jù)進(jìn)行實(shí)驗(yàn)。參考WMM世界地磁模型中南京地區(qū)的地磁場(chǎng)參數(shù),定義磁傾角為48.12°,地磁場(chǎng)總量為50 000 nT,軟磁干擾誤差矩陣與硬磁干擾誤差向量分別為:

(13)

參照以上給定參數(shù)生成了240組的三維干擾磁測(cè)數(shù)據(jù),同時(shí)為模擬傳感器測(cè)量噪聲,在三維磁場(chǎng)數(shù)據(jù)和θ、γ數(shù)據(jù)上分別疊加滿足零均值分布,標(biāo)準(zhǔn)差分別為30 nT和0.1°的高斯噪聲。生成磁場(chǎng)測(cè)量數(shù)據(jù)三維顯示如圖2所示,圖2中球面為理論地磁場(chǎng)的測(cè)量圓球面。

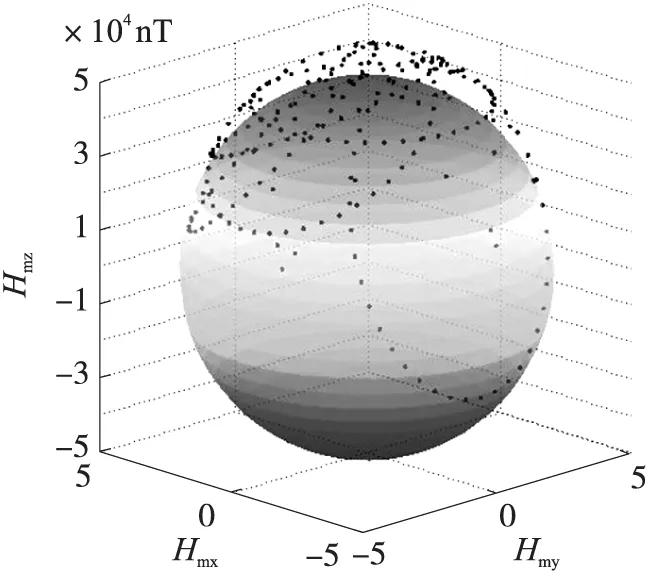
圖2 仿真數(shù)據(jù)三維分布圖

首先使用最小二乘橢球擬合方法求解誤差模型參數(shù),并采用常見的上三角、下三角與對(duì)稱矩陣3種形式軟磁干擾矩陣對(duì)地磁場(chǎng)測(cè)量數(shù)據(jù)修正,然后在此修正數(shù)據(jù)基礎(chǔ)上運(yùn)用本文提出的優(yōu)化方法對(duì)剩余的非對(duì)準(zhǔn)誤差角β進(jìn)行估計(jì)。其中PSO參數(shù)取值,M、ω、c1、c2分別為40、0.5、2、2。表1為誤差角ζ(°)估計(jì)結(jié)果。

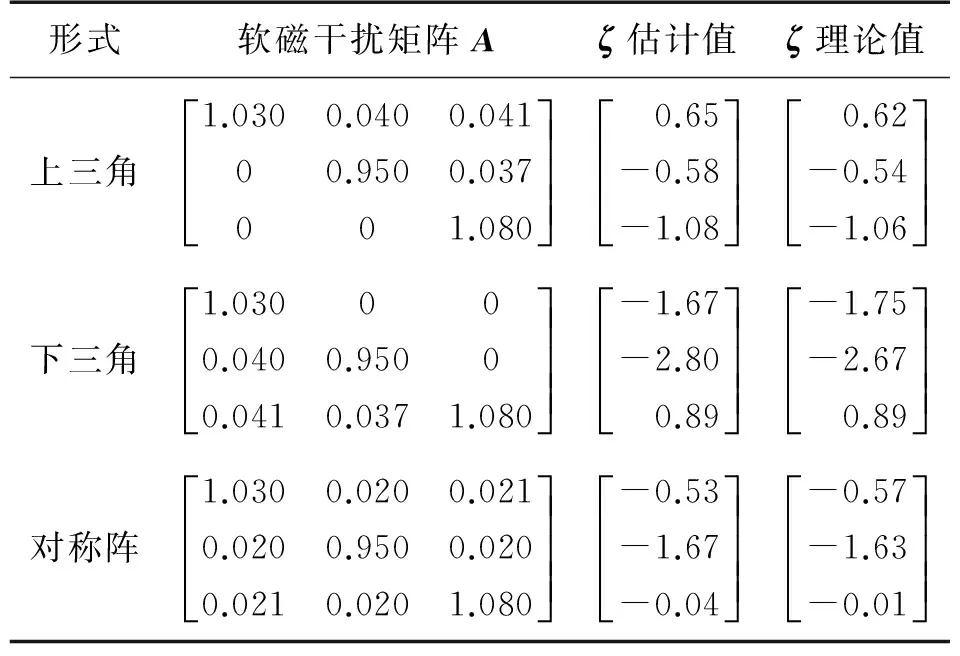
表1 不同分解情況下非對(duì)準(zhǔn)誤差角估計(jì)值

由表1可知:ζ估計(jì)值與理論值基本一致,表明優(yōu)化方法可以有效地估計(jì)缺失參數(shù)。

為驗(yàn)證優(yōu)化方法磁航向補(bǔ)償精度,采用表1中β估計(jì)值優(yōu)化后的軟磁干擾矩陣,對(duì)俯仰角-30°傾斜姿態(tài)處旋轉(zhuǎn)采集的地磁數(shù)據(jù)進(jìn)行修正,并與橢球假設(shè)方法的補(bǔ)償結(jié)果進(jìn)行對(duì)比,對(duì)比結(jié)果如圖3所示。圖3中,由于在不同形式軟磁干擾系數(shù)矩陣修正數(shù)據(jù)基礎(chǔ)上進(jìn)行優(yōu)化補(bǔ)償后的結(jié)果非常接近(<0.1°),因此使用一條曲線表示(“優(yōu)化后”所對(duì)應(yīng)曲線)。由圖3可知,補(bǔ)償前磁航向剩余誤差的范圍較大,橢球假設(shè)補(bǔ)償后誤差范圍減小,同時(shí)不同矩陣形式的補(bǔ)償效果不相同,使用優(yōu)化補(bǔ)償方法進(jìn)一步補(bǔ)償后的誤差范圍明顯小于橢球假設(shè)法。

圖3 磁航向誤差補(bǔ)償比對(duì)圖

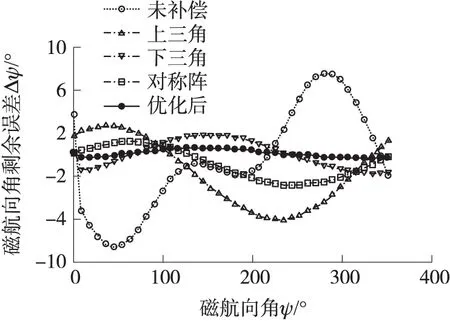
圖4 不同軟磁干擾情況磁航向誤差補(bǔ)償結(jié)果

而橢球擬合方法補(bǔ)償精度的不一致性有:上三角形式>對(duì)稱陣形式>下三角形式,以地磁場(chǎng)測(cè)量軸系的x軸與z軸進(jìn)行分析。如式(13)所示,軟磁干擾系數(shù)矩陣A的上半部分對(duì)角元素的數(shù)值明顯大于其下半部分對(duì)角元素的數(shù)值,相比x軸誤差對(duì)z軸的影響,z軸誤差對(duì)x軸影響要大得多。而下三角矩陣將上半部分對(duì)角元素?cái)?shù)值設(shè)置為0,忽略了z軸誤差對(duì)x軸影響,故其補(bǔ)償精度最差,而上三角矩陣補(bǔ)償精度最高。圖4給出了矩陣A的上半部分對(duì)角元素的數(shù)值小于其下半部分對(duì)角元素的補(bǔ)償情況,可以明顯看出此時(shí)下三角形式補(bǔ)償效果好于上三角形式。由于實(shí)際應(yīng)用中無法預(yù)知軟磁干擾矩陣接近于何種矩陣形式,而較難選取適合形式使得橢球假設(shè)方法的補(bǔ)償效果達(dá)到最佳,這也是實(shí)際應(yīng)用中橢球假設(shè)方法的局限性所在。

4 實(shí)驗(yàn)驗(yàn)證

為了驗(yàn)證本文提出優(yōu)化方法的實(shí)際性能,利用PNI公司的TCM-XB數(shù)字磁羅盤在三軸轉(zhuǎn)臺(tái)上進(jìn)行實(shí)驗(yàn),磁羅盤內(nèi)部加速度計(jì)實(shí)驗(yàn)前已進(jìn)行標(biāo)定,姿態(tài)測(cè)量精度±0.2°,轉(zhuǎn)臺(tái)角度分辨率為0.01°。實(shí)驗(yàn)前,將鋼鐵構(gòu)件固定于磁羅盤附近,用于模擬產(chǎn)生載體干擾磁場(chǎng)。由于實(shí)際中數(shù)字磁羅盤的應(yīng)用對(duì)象不會(huì)產(chǎn)生較大幅度的傾角,因此實(shí)驗(yàn)設(shè)計(jì)θ、γ的變化范圍為±45°。

實(shí)驗(yàn)步驟:在水平與俯仰角±20°、±40° 5種姿態(tài)下分別旋轉(zhuǎn)一周采集地磁場(chǎng)數(shù)據(jù)與姿態(tài)數(shù)據(jù),間隔15°,同時(shí)在姿態(tài)范圍內(nèi)隨機(jī)采集40組數(shù)據(jù),共160組;按算法計(jì)算分別橢球假設(shè)模型參數(shù)與優(yōu)化補(bǔ)償模型參數(shù),然后按前文步驟對(duì)以上地磁數(shù)據(jù)進(jìn)行修正,以轉(zhuǎn)臺(tái)輸出的航向作為標(biāo)準(zhǔn)角度計(jì)算磁航向剩余誤差。為了方便說明,以俯仰角為-20°的傾斜姿態(tài)為例,如圖5所示。

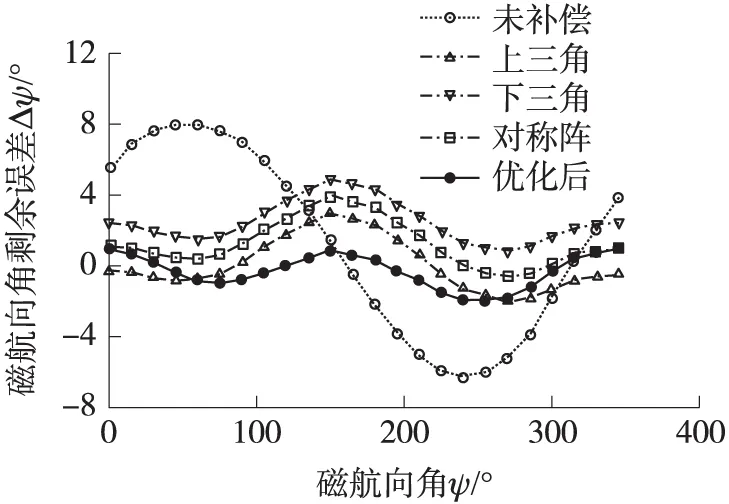
圖5 俯仰角-20°時(shí)磁航向誤差補(bǔ)償結(jié)果

圖5中,未補(bǔ)償時(shí)磁航向最大誤差達(dá)到7.8°,誤差標(biāo)準(zhǔn)差5.15°;橢球假設(shè)方法中,軟磁干擾矩陣取上三角形式時(shí)補(bǔ)償效果最佳,最大誤差2.9°,標(biāo)準(zhǔn)差1.2°,取下三角形式最差,最大誤差4.8°,標(biāo)準(zhǔn)差1.5°;優(yōu)化補(bǔ)償后磁航向最大誤差進(jìn)一步減小到1.9°,標(biāo)準(zhǔn)差減小到1.1°。

5 結(jié)論

應(yīng)用于數(shù)字磁羅盤的全姿態(tài)羅差補(bǔ)償方法存在著一定局限性,補(bǔ)償精度受到制約,本文在分析局限性的基礎(chǔ)上提出了一種羅差自主優(yōu)化補(bǔ)償方法。仿真結(jié)果表明,常規(guī)橢球假設(shè)補(bǔ)償方法估計(jì)參數(shù)存在缺失,不同分解形式的軟磁矩陣的補(bǔ)償效果不一致,而優(yōu)化補(bǔ)償方法能夠有效估計(jì)3個(gè)缺失參數(shù),唯一確定原模型中的12參數(shù)。實(shí)物實(shí)驗(yàn)結(jié)果顯示,傾角20°姿態(tài)下,優(yōu)化方法將常規(guī)橢球假設(shè)方法補(bǔ)償?shù)淖畲笳`差由4.8°降至1.9°,誤差標(biāo)準(zhǔn)差由1.5°降至1.1°,提出的優(yōu)化方法有效估計(jì)橢球假設(shè)方法中剩余非對(duì)準(zhǔn)誤差,進(jìn)一步提高磁航向補(bǔ)償精度。

本文提出的優(yōu)化方法參考水平坐標(biāo)系中地磁場(chǎng)分量這一自然基準(zhǔn),利用分量不變性的約束估計(jì)出缺失參數(shù),而無需借助外部輔助姿態(tài),保持了橢球假設(shè)方法原有自主補(bǔ)償?shù)膬?yōu)勢(shì),可用于磁羅盤現(xiàn)場(chǎng)校正的場(chǎng)合。

[1] Moulin M,Guodon J C,Marsy J M,et al. Process for Compensating the Magnetic Disturbances in the Determination of a Magnetic Heading,and Devices for Carrying Out This Process. United States:No.4414753,1983-11-15.

[2] 李智,李翔. 基于橢球假設(shè)的三軸電子羅盤羅差補(bǔ)償研究[J]. 儀器儀表學(xué)報(bào),2011,32(10):2210-2215.

[3] Pylv?n?inen T. Automatic and Adaptive Calibration of 3D Field Sensors[J]. Applied Mathematical Modelling,2008,32(4):575-587.

[4] Fang J,Sun H,Cao J,et al. A Novel Calibration Method of Magnetic Compass Based on Ellipsoid Fitting[J]. IEEE Transactions on Instrumentation and Measurement,2011,60(6):2053-2061.

[5] 劉玉霞,周軍,葛致磊. 基于軌跡約束的地磁場(chǎng)測(cè)量誤差修正方法[J]. 中國(guó)慣性技術(shù)學(xué)報(bào),2012,20(2):205-210.

[6] 郭鵬飛,任章,邱海韜,等. 一種十二位置不對(duì)北的磁羅盤標(biāo)定方法[J]. 中國(guó)慣性技術(shù)學(xué)報(bào),2008,15(5):598-601.

[7] 郭鵬飛,華春紅,任章,等. 基于遞推最小二乘的航姿系統(tǒng)羅差校正[J]. 中國(guó)慣性技術(shù)學(xué)報(bào),2008,16(1):24-27.

[8] 龍禮,張合,劉建敬. 姿態(tài)檢測(cè)地磁傳感器誤差分析與補(bǔ)償方法[J]. 中國(guó)慣性技術(shù)學(xué)報(bào),2013,21(1):80-83.

[9] Bonnet S,Bassompierre C,Godin C,et al. Calibration Methods for Inertial and Magnetic Sensors[J]. Sensors and Actuators A:Physical,2009,156(2):302-311.

[10] 范成葉,李杰,陳文蓉,等. 電子羅盤安裝誤差標(biāo)定與補(bǔ)償方法研究[J]. 傳感技術(shù)學(xué)報(bào),2013,26(5):622-626.

[11] 焦巍,劉光斌,張金生,等. 基于粒子群算法的地磁匹配航跡規(guī)劃[J]. 系統(tǒng)工程理論與實(shí)踐,2010,30(11):2106-2111.

洪琪璐(1990-),女,浙江金華人,現(xiàn)為南京理工大學(xué)儀器儀表工程專業(yè)在讀研究生,主要研究方向?yàn)闊o線通訊技術(shù),xichexue@yeah.net;

張愛軍(1978-),男,黑龍江慶安人,博士,副教授,主要研究方向?yàn)閷?dǎo)航信息處理技術(shù)、嵌入式開發(fā)、超高頻無線射頻技術(shù)。

MethodtoMagneticDeviationSelf-OptimalCompensationofDigitalMagneticCompass

HONGQilu1,ZHANGAijun1*,WANGChangming1

(School of mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094 China)

A magnetic deviation self-optimal method based on thecomponent of geomagnetic field was put forward to improve the compensation precision of all-attitude digital magnetic compass. According to magnetic deviation compensation model,a limited compensation ellipsoid matching error wasanalyzed and an optimal compensation model including missing parameters was established based on the missing parameters andresidual error analysis. In view of the nonlinear optimal model,the particle swarm optimization(PSO)was introduced to estimate the model parameters,and the results of numerical simulation was proved that the PSO couldbe estimated the missing parameters effectively. All experiment results showed that the process of optimal compensation did not need external auxiliary posture information. When the pitching angle was -20°,the maximum error was reduced from 4.8° to 1.9° and the standard deviation was reduced from 1.5° to 1.1° in the usage of optimal compensation method based on ellipsoid matching error compensation method.

digital magnetic compass;magnetic deviation;nonlinear;PSO

2017-03-01修改日期:2017-06-05

U666.1

:A

:1004-1699(2017)09-1364-05

10.3969/j.issn.1004-1699.2017.09.011