基于約簡(jiǎn)策略與自適應(yīng)SVDD的無(wú)線傳感網(wǎng)絡(luò)離群檢測(cè)方法*
魏 暢,李光輝
(1.江南大學(xué)物聯(lián)網(wǎng)工程學(xué)院,江蘇 無(wú)錫 214122;2.江蘇省無(wú)線傳感網(wǎng)高技術(shù)研究重點(diǎn)實(shí)驗(yàn)室,南京 210003;3.物聯(lián)網(wǎng)技術(shù)應(yīng)用教育部工程技術(shù)研究中心,江蘇 無(wú)錫 214122)
基于約簡(jiǎn)策略與自適應(yīng)SVDD的無(wú)線傳感網(wǎng)絡(luò)離群檢測(cè)方法*
魏 暢1,3,李光輝1,2,3*
(1.江南大學(xué)物聯(lián)網(wǎng)工程學(xué)院,江蘇 無(wú)錫 214122;2.江蘇省無(wú)線傳感網(wǎng)高技術(shù)研究重點(diǎn)實(shí)驗(yàn)室,南京 210003;3.物聯(lián)網(wǎng)技術(shù)應(yīng)用教育部工程技術(shù)研究中心,江蘇 無(wú)錫 214122)
無(wú)線傳感網(wǎng)絡(luò)經(jīng)常被部署于條件惡劣、無(wú)人值守的環(huán)境中,受到惡劣天氣、軟硬件故障、能量不足或者惡意攻擊等因素的影響,傳感器節(jié)點(diǎn)感知數(shù)據(jù)的缺失或錯(cuò)誤難以避免。因此,傳感器數(shù)據(jù)流的離群檢測(cè)對(duì)于提高系統(tǒng)可用性至關(guān)重要。提出一種基于約簡(jiǎn)策略與自適應(yīng)SVDD(Support Vector Data Description)的離群檢測(cè)方法(RASVDD),該方法首先使用基于馬氏距離標(biāo)準(zhǔn)的方法約簡(jiǎn)數(shù)據(jù)集,有效地減少了訓(xùn)練樣本;然后利用基于數(shù)據(jù)分布密度準(zhǔn)則和數(shù)據(jù)流時(shí)間相關(guān)性自適應(yīng)更新決策模型。針對(duì)Intel Berkeley數(shù)據(jù)集及SensorScope System數(shù)據(jù)集的仿真實(shí)驗(yàn)表明,RASVDD的離群檢測(cè)正確率TPR(True Positive Rate)平均達(dá)98%,誤報(bào)率FPR(False Positive Rate)平均僅為1%,并且與傳統(tǒng)的SVDD算法相比,RASVDD 決策模型訓(xùn)練時(shí)間減少了20%以上。
無(wú)線傳感網(wǎng)絡(luò);數(shù)據(jù)約簡(jiǎn);SVDD;離群檢測(cè);仿真
21世紀(jì)電子信息和無(wú)線通信技術(shù)取得了巨大發(fā)展,使得由高靈敏且低能耗的傳感器節(jié)點(diǎn)組成的無(wú)線傳感網(wǎng)絡(luò)逐漸應(yīng)用于實(shí)際生活的各個(gè)領(lǐng)域。與傳統(tǒng)網(wǎng)絡(luò)相比,傳感器節(jié)點(diǎn)具有很強(qiáng)的資源限制,在能量、內(nèi)存、計(jì)算能力和通信帶寬方面都存在很大的局限性。傳感器網(wǎng)絡(luò)經(jīng)常被部署在惡劣環(huán)境下,傳感器數(shù)據(jù)流的質(zhì)量不可避免地受到惡劣天氣、軟硬件故障、能量不足或者惡意攻擊等因素的影響[1]。針對(duì)傳感器數(shù)據(jù)流進(jìn)行離群檢測(cè),不僅有助于對(duì)傳感器網(wǎng)絡(luò)健康狀況進(jìn)行檢測(cè)與故障修復(fù)[2],而且能夠及時(shí)有效地為用戶(hù)提供其感興趣的事件,這對(duì)于保證傳感器網(wǎng)絡(luò)的數(shù)據(jù)質(zhì)量和科學(xué)決策具有重要意義。
在無(wú)線傳感器網(wǎng)絡(luò)中,某些傳感器節(jié)點(diǎn)觀測(cè)值顯著偏離于正常模型或者預(yù)期結(jié)果,通常被稱(chēng)為離群(outlier)數(shù)據(jù)[3]。近年來(lái),國(guó)內(nèi)外學(xué)者對(duì)無(wú)線傳感網(wǎng)絡(luò)離群檢測(cè)方法進(jìn)行了深入研究[4-5],這些方法大致可分為基于統(tǒng)計(jì)的方法、基于最近鄰的方法、基于聚類(lèi)的方法、基于分類(lèi)的方法、基于譜分解的方法等類(lèi)型[6-7]。由于SVDD算法在二分類(lèi)方面的性能優(yōu)勢(shì),已被一些學(xué)者引入到傳感器網(wǎng)絡(luò)離群檢測(cè)領(lǐng)域。SVDD由Tax[8-9]等人首次提出,是對(duì)SVM(Support Vector Machine)進(jìn)行推廣的算法,其基本思想是尋找到一個(gè)最小圓使所有目標(biāo)類(lèi)均可以落入該圓內(nèi),該圓的邊界即為決策邊界,用于區(qū)分離群點(diǎn)和正常點(diǎn)。SVDD和SVM相似,需要求解二次優(yōu)化QP(Quadratic Programming)問(wèn)題,因此其時(shí)間復(fù)雜度為O(n3),空間復(fù)雜度為O(n2),這樣高的計(jì)算復(fù)雜度難以適用于資源受限的無(wú)線傳感器網(wǎng)絡(luò)。因此,許多學(xué)者研究了如何優(yōu)化SVDD算法的性能,例如,孫文柱等[10]采用K-mean聚類(lèi)方法確定樣本聚類(lèi)中心,并對(duì)所有樣本依其聚類(lèi)中心距離排序,而后由外向內(nèi)等間隔依次選取樣本構(gòu)成約減核矩陣,對(duì)數(shù)據(jù)集進(jìn)行約簡(jiǎn)。Hu[11]利用鄰居節(jié)點(diǎn)間角度和密度的關(guān)系,實(shí)現(xiàn)尋找樣本模型的決策邊緣,以此來(lái)約簡(jiǎn)訓(xùn)練集樣本。梁錦錦[12]和謝迎新[13]考慮到?jīng)Q策邊界僅由少量分布在樣本集邊緣的數(shù)據(jù)決定,采用衡量中心點(diǎn)和其余點(diǎn)的歐氏距離,約減距離較大的樣本點(diǎn)。Platt[14]和Fan[15]提出SMO_SVDD思想,用來(lái)優(yōu)化訓(xùn)練規(guī)則,其利用違背KKT(Karush-Kuhn-Tucker condition)條件的Lagrange乘子兩兩進(jìn)行優(yōu)化,直到所有乘子都滿(mǎn)足KKT條件,此時(shí)所得乘子為QP問(wèn)題的最優(yōu)解。Liu[16]和周勝明[17]集中于尋找一個(gè)與決策模型相似的超球或超橢球替代決策函數(shù),有效地將決策復(fù)雜度降低為O(1),但該決策優(yōu)化方法對(duì)不規(guī)則模型的性能較差。對(duì)于無(wú)線傳感器網(wǎng)絡(luò),除需考慮上述問(wèn)題外,還需注意其隨時(shí)間不斷變化的數(shù)據(jù)流[1],若使用一次訓(xùn)練的方法,隨著數(shù)據(jù)流的變化,決策模型的準(zhǔn)確性會(huì)逐漸降低。針對(duì)以上問(wèn)題,本文提出了一種基于約簡(jiǎn)策略與自適應(yīng)SVDD的無(wú)線傳感器網(wǎng)絡(luò)離群檢測(cè)方法(RASVDD),該方法不僅可以節(jié)省決策模型的訓(xùn)練時(shí)間,而且能夠有效提高離群檢測(cè)的準(zhǔn)確率。
1 預(yù)備知識(shí)
1.1 SVDD算法原理
給定一個(gè)包含n個(gè)數(shù)據(jù)點(diǎn)的數(shù)據(jù)集X={x1,x2,…,xn},SVDD的核心思想[8-9]是找到一個(gè)以a為圓心,R為半徑的最小圓,該圓能夠全部或盡可能多地包含X中的數(shù)據(jù)點(diǎn)。故該優(yōu)化問(wèn)題可以描述為:
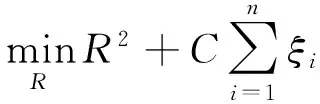
(1)
式中:a為圓心;R為半徑;ξi≥0為松弛變量;C>0為懲罰因子,用于實(shí)現(xiàn)圓的大小和包含樣本數(shù)間的折中。SVDD的幾何模型如圖1所示,圖中黑色點(diǎn)為集合X中的數(shù)據(jù)樣本。
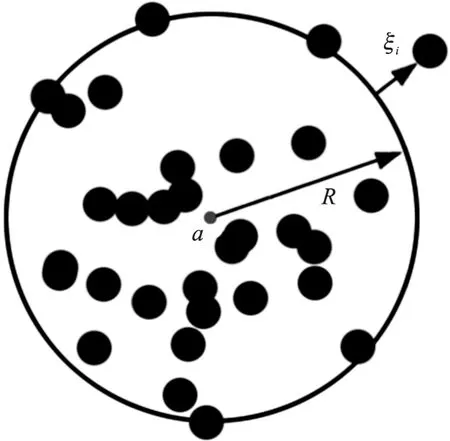
圖1 SVDD幾何模型
上述優(yōu)化問(wèn)題可通過(guò)Lagrange乘子法求解,構(gòu)建Lagrange方程:
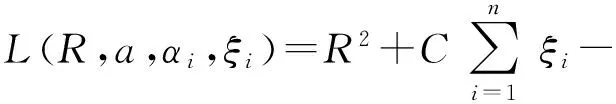
(2)
式中:αi≥0,γi≥0,分別令L關(guān)于R,a,ξi的偏導(dǎo)數(shù)為零,可得:
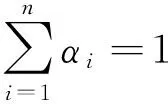
(3)
將式(3)代入式(2)中得:
(4)
然而,該方法只對(duì)輸入空間為類(lèi)圓形的數(shù)據(jù)集具有較好的性能。當(dāng)輸入空間為非圓形分布時(shí),該方法不能達(dá)到理想的性能,故引入核函數(shù)來(lái)改善算法的適用性。找到一個(gè)合適的映射φ將輸入樣本xi映射到一個(gè)高維的特征空間φ(xi),在高維空間找到一個(gè)超球體盡可能多地包圍輸入空間的點(diǎn)。故式(4)中的內(nèi)積(xi·xj)可以使用核函數(shù)K(xi,xj)替換。本文選用高斯核函數(shù):
(5)
此時(shí),式(4)可以轉(zhuǎn)化為L(zhǎng)agrange對(duì)偶問(wèn)題:
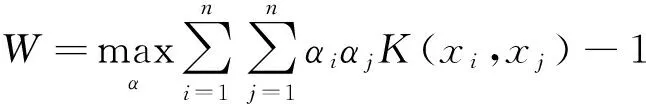
(6)
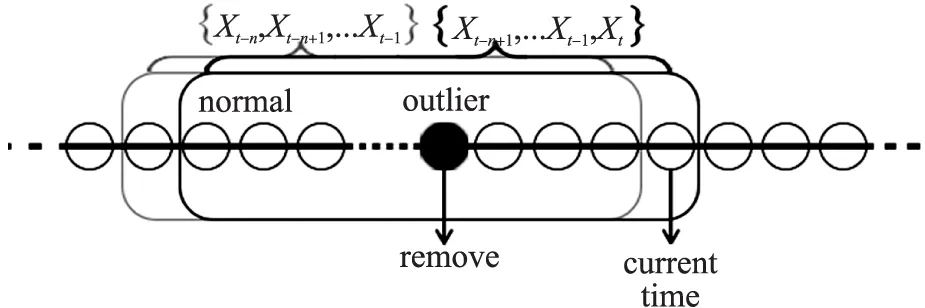
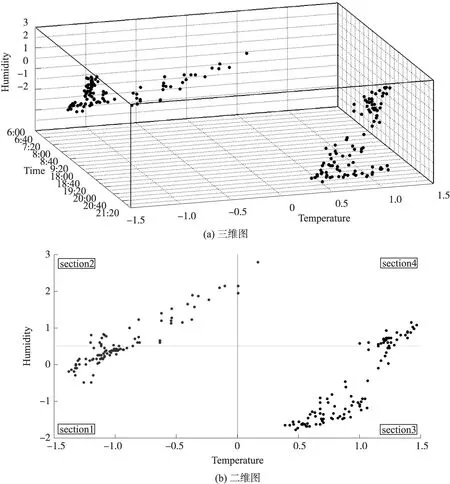
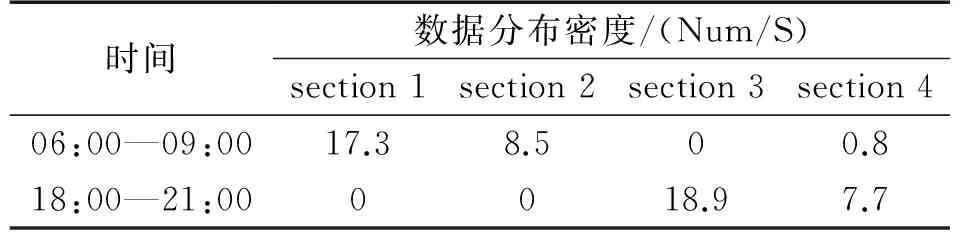
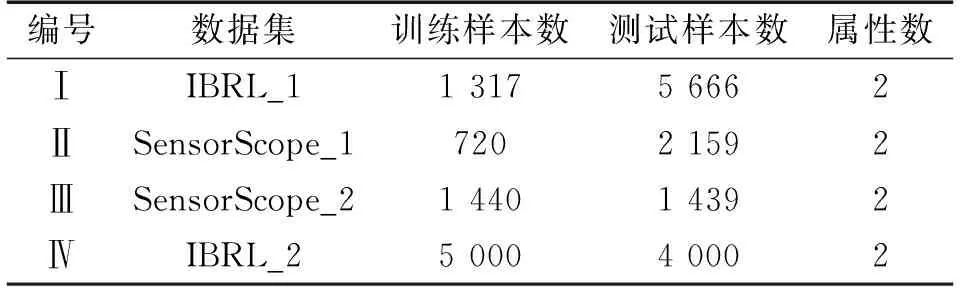
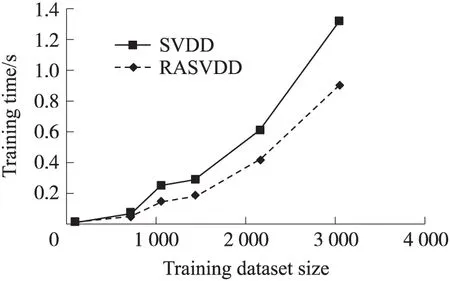
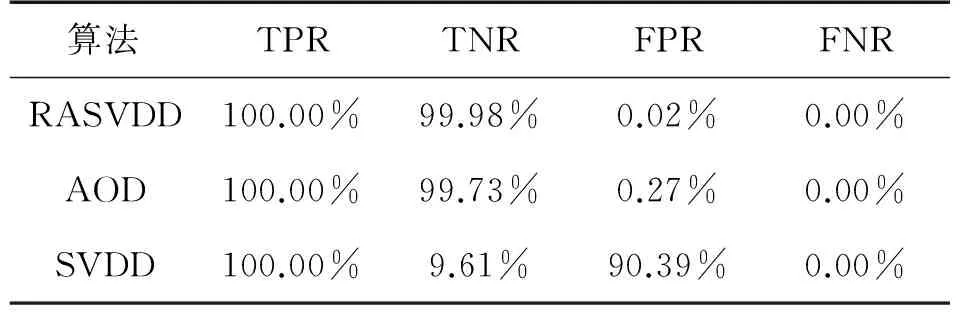
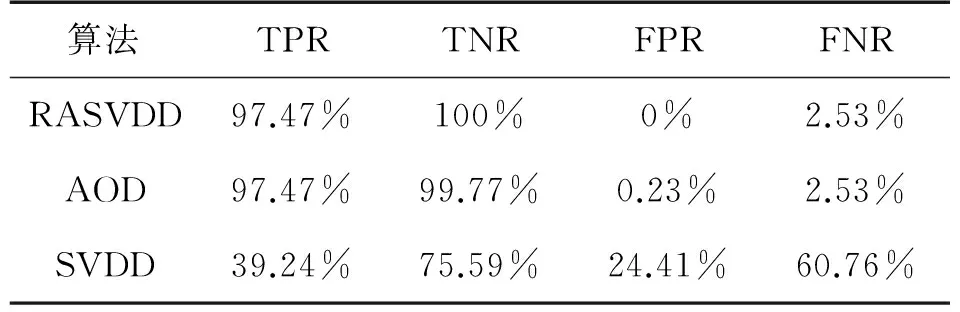
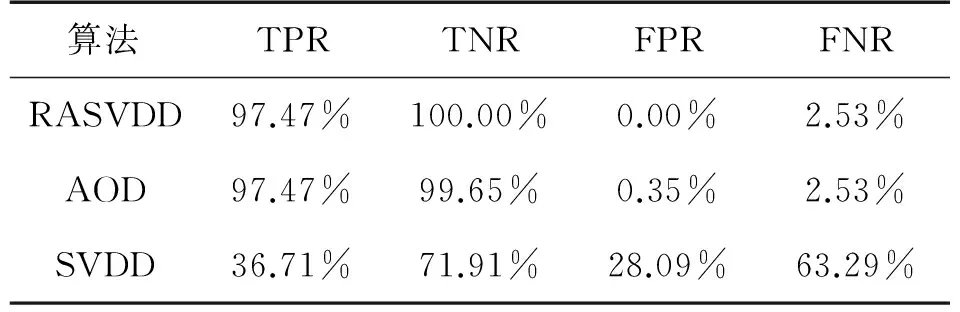
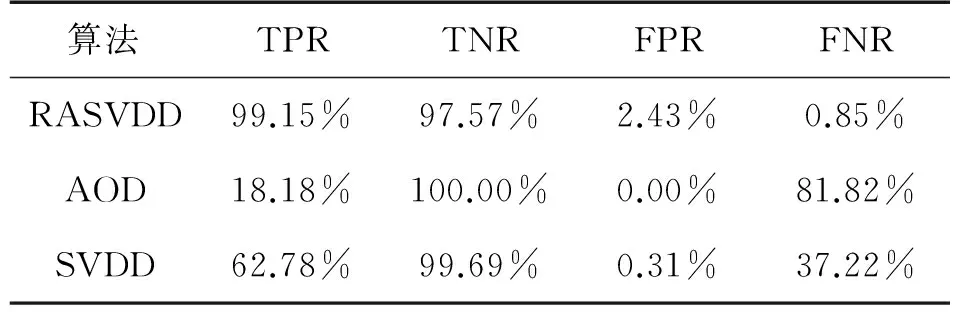
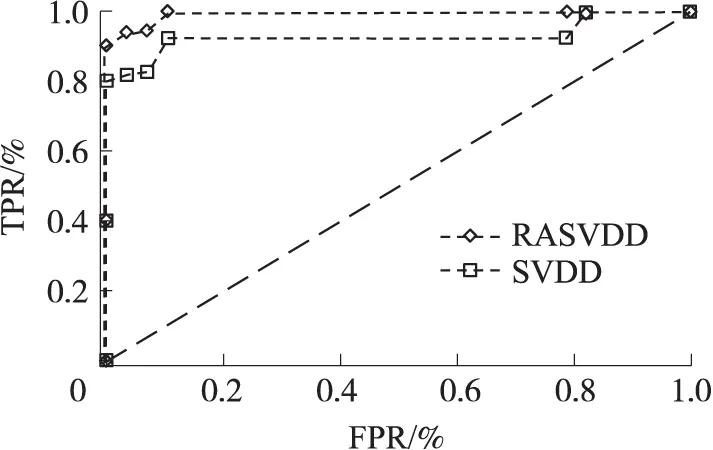
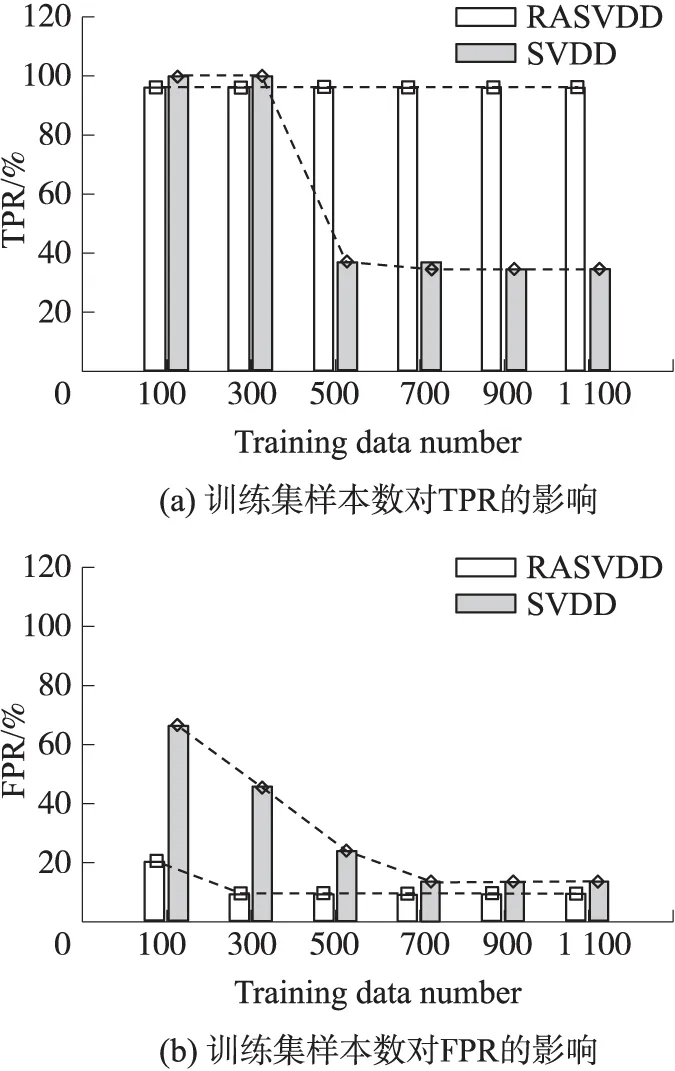
式(6)為典型的二次優(yōu)化問(wèn)題,其目標(biāo)集合α=(α1,α2,…,αn)可以被分為三類(lèi):αi=0,落在圓內(nèi)的正常數(shù)據(jù)點(diǎn);0<αi f(xi)=sgn(‖φ(xi)-a‖2-R2) (7) 由式(7)可得:當(dāng)f(xi)≤0時(shí),xi被分類(lèi)為正常數(shù)據(jù)點(diǎn);當(dāng)f(xi)>0時(shí),xi被分類(lèi)為離群數(shù)據(jù)點(diǎn)。 1.2 基于SMO的SVDD算法原理 SVDD算法需要求解二次優(yōu)化問(wèn)題,因此其時(shí)間復(fù)雜度為O(n3),空間復(fù)雜度為O(n2),難以適用于資源受限的無(wú)線傳感網(wǎng)絡(luò)。文獻(xiàn)[14-15]研究了SMO(Sequential Minimal Optimization)算法在SVM中的應(yīng)用,其基本思想是:如果所有Lagrange乘子都滿(mǎn)足此優(yōu)化問(wèn)題的KKT條件,則此時(shí)的乘子為問(wèn)題的最優(yōu)解,因?yàn)镵KT條件是Lagrange對(duì)偶問(wèn)題(6)的充分必要條件。否則,從樣本集中選擇兩個(gè)乘子,固定其余乘子,針對(duì)這兩個(gè)乘子構(gòu)建二次規(guī)劃問(wèn)題,該問(wèn)題可通過(guò)解析方法求解。SMO算法將原問(wèn)題不斷分解為子問(wèn)題并對(duì)子問(wèn)題求解,進(jìn)而達(dá)到求解原問(wèn)題的目的,如此能大大提高算法的計(jì)算速度。下面介紹SMO_SVDD算法工作集乘子選擇策略及Lagrange乘子優(yōu)化策略。 1.2.1 工作集乘子的選擇策略 根據(jù)KKT條件得:當(dāng)αi=0時(shí),‖a-φ(x)‖2 xs=argmax(‖c-φ(xi)‖2|αi (8) 若KKT條件成立,則有g(shù)(xt)≥g(xs),故在算法迭代過(guò)程中都有g(shù)(xs)>g(xt)+δ。 1.2.2Lagrange乘子的優(yōu)化策略 (9) 令αt=ζ-αs,得: (10) 對(duì)式(10)中的αs求二階導(dǎo)數(shù),得: (11) (12) 傳統(tǒng)的SVDD是一種優(yōu)秀的二分類(lèi)算法,但應(yīng)用于資源受限的無(wú)線傳感網(wǎng)絡(luò)時(shí),其計(jì)算復(fù)雜度偏高。為降低計(jì)算復(fù)雜度,提高離群檢測(cè)的準(zhǔn)確率,本文提出了一種基于約簡(jiǎn)策略和自適應(yīng)SVDD的傳感網(wǎng)絡(luò)離群檢測(cè)方法(RASVDD),該方法包括基于馬氏距離標(biāo)準(zhǔn)的訓(xùn)練集約簡(jiǎn)策略和基于數(shù)據(jù)分布密度的自適應(yīng)離群檢測(cè)機(jī)制,適用于低密度非均勻部署的無(wú)線傳感器網(wǎng)絡(luò)。 2.1 訓(xùn)練集的約簡(jiǎn)策略 原Lagrange對(duì)偶問(wèn)題的解具有極大的稀疏性,因此有效并完整地選擇與邊界相關(guān)的子數(shù)據(jù)集,即求解α>0的點(diǎn),對(duì)于整體訓(xùn)練性能的提高非常關(guān)鍵。受文獻(xiàn)[12-13]的啟發(fā),本文采用基于馬氏距離標(biāo)準(zhǔn)的策略約簡(jiǎn)數(shù)據(jù)集,用以縮短決策模型訓(xùn)練時(shí)間。 馬氏距離由印度統(tǒng)計(jì)學(xué)家Mahalanobis P C提出,是一種有效地計(jì)算兩個(gè)未知樣本集相似度的方法,由于其考慮了各屬性間的聯(lián)系,故相對(duì)歐式距離有明顯優(yōu)勢(shì)。另外,由于高斯核函數(shù)的映射過(guò)程很好地保留了鄰居間的相互關(guān)系,故約簡(jiǎn)數(shù)據(jù)集可在樣本空間進(jìn)行,不必映射到高維空間。 對(duì)于給定的訓(xùn)練集Train={X1,X2,…,Xn},任一數(shù)據(jù)樣本Xi={Xi1,Xi2,…,Xid},其中d為樣本包含的屬性個(gè)數(shù)。μ={μ1,μ2,…,μd}為每個(gè)屬性的數(shù)學(xué)期望所構(gòu)成的向量,Σ為協(xié)方差矩陣。計(jì)算公式如下: μj=E(Xij)i=1,…,n;j=1,…,d. (13) 定義1樣本點(diǎn)與訓(xùn)練數(shù)據(jù)集數(shù)學(xué)期望間的馬氏距離MD(Xi): (14) 本文使用定義1作為衡量標(biāo)準(zhǔn),約簡(jiǎn)訓(xùn)練集中與決策邊界無(wú)關(guān)的樣本點(diǎn),約簡(jiǎn)策略算法如表1所示。 表1 基于馬氏距離標(biāo)準(zhǔn)的約簡(jiǎn)策略算法 2.2 自適應(yīng)檢測(cè)機(jī)制 考慮到真實(shí)部署的無(wú)線傳感網(wǎng)絡(luò)受自然環(huán)境影響較大,其數(shù)據(jù)流的演變過(guò)程具有一定的隨機(jī)性,若采用一次訓(xùn)練的方法進(jìn)行離群檢測(cè),決策模型的魯棒性和泛化能力將會(huì)隨著時(shí)間的推移逐漸退化。為了解決該問(wèn)題,本文提出了一種基于數(shù)據(jù)分布密度的自適應(yīng)離群檢測(cè)機(jī)制(ASVDD),使其能夠隨著傳感器數(shù)據(jù)流的演變過(guò)程自動(dòng)更新決策模型,從而提高傳感網(wǎng)絡(luò)離群檢測(cè)的準(zhǔn)確率。 2.2.1 數(shù)據(jù)流的滑動(dòng)窗口模型 ASVDD使用滑動(dòng)窗口模型處理傳感器數(shù)據(jù)流[18],其特點(diǎn)在于處理數(shù)據(jù)窗口的大小固定,滑動(dòng)窗口的終點(diǎn)始終為當(dāng)前時(shí)刻,即加入新數(shù)據(jù)的同時(shí)移除舊數(shù)據(jù)。滑動(dòng)窗口可以保證模型訓(xùn)練一直使用最新的傳感數(shù)據(jù),使得決策模型與當(dāng)前數(shù)據(jù)分布情況保持高度一致,能夠有效提高檢測(cè)效率。 如圖2所示的滑動(dòng)窗口模型,其中窗口大小為n,即滑動(dòng)窗口buffer中存儲(chǔ)有n個(gè)數(shù)據(jù)。若在t-1時(shí)刻buffer中存儲(chǔ)數(shù)據(jù){Xt-n,Xt-n+1,…,Xt-1},則在當(dāng)前時(shí)刻t時(shí),buffer中將移除Xt-n,并加入當(dāng)前時(shí)刻數(shù)據(jù)Xt,此時(shí)buffer中存儲(chǔ)數(shù)據(jù){Xt-n+1,…,Xt-1,Xt}。在本算法中,對(duì)于離群值采用直接移除不加入滑動(dòng)窗口的方式。 圖2 滑動(dòng)窗口模型 2.2.2 基于數(shù)據(jù)分布密度的決策模型更新準(zhǔn)則 決策模型更新準(zhǔn)則是有效提高檢測(cè)效率的關(guān)鍵,Zhang[7]論文中采用基于離群點(diǎn)的更新準(zhǔn)則,即當(dāng)出現(xiàn)離群點(diǎn)則更新決策模型,但該算法僅考慮離群點(diǎn)的出現(xiàn)不能充分說(shuō)明決策模型更新的需要。故本文提出基于數(shù)據(jù)分布密度的更新準(zhǔn)則,依據(jù)數(shù)據(jù)分布密度判斷決策模型是否需要更新,保證算法更新及時(shí)有效。 如圖3所示,為SensorScopeSystem數(shù)據(jù)集2號(hào)節(jié)點(diǎn)2007年9月15日歸一化后的溫度和濕度數(shù)據(jù),采樣周期為2min,其中紅色點(diǎn)為6點(diǎn)到9點(diǎn)的數(shù)據(jù)分布情況,藍(lán)色點(diǎn)為18點(diǎn)到21點(diǎn)的數(shù)據(jù)分布情況。圖3(b)為圖3(a)投影到Y(jié)(溫度)軸和Z(濕度)軸后的圖像,由圖3(b)可以清楚的看到在該時(shí)間區(qū)間樣本點(diǎn)的空間分布情況。 定義2空間域Ω的數(shù)據(jù)分布密度ρ是指Ω中包含的數(shù)據(jù)樣本個(gè)數(shù)Num與Ω的面積S之比: ρ=Num/S (15) 圖3 不同時(shí)間段數(shù)據(jù)分布情況 將上述數(shù)據(jù)空間劃分為4個(gè)子空間域section1~section4,各個(gè)子空間域在時(shí)間段6點(diǎn)到9點(diǎn)和18點(diǎn)到21點(diǎn)的數(shù)據(jù)分布密度如表2所示。 表2 不同時(shí)間段數(shù)據(jù)分布密度 ASVDD更新準(zhǔn)則為:當(dāng)Δρ超過(guò)閾值τ時(shí)應(yīng)更新決策模型使其與當(dāng)前時(shí)刻正常數(shù)據(jù)流分布情況保持一致。故構(gòu)建一個(gè)隨數(shù)據(jù)分布密度特征變化的SVDD分類(lèi)面,即能夠有效地完成決策模型的自適應(yīng)更新,ASVDD算法步驟如下: Step 1 將數(shù)據(jù)空間劃分為m個(gè)子空間域,即section(1),section(2),…,section(m); Step 2 計(jì)算訓(xùn)練集樣本在各個(gè)子空間域中的數(shù)據(jù)分布密度,記為ρ_old; Step 3 計(jì)算當(dāng)前時(shí)刻數(shù)據(jù)所屬子空間域section(i),i=1,2,…,m,更新數(shù)據(jù)分布密度,記為ρ_new; Step 4 計(jì)算Δρ=|ρ_new-ρ_old|; Step 5 若Δρ≥τ,則使用當(dāng)前滑動(dòng)窗口buffer中的數(shù)據(jù)更新決策模型,并把此時(shí)的ρ_old更新為ρ_new,繼續(xù)執(zhí)行step3;若Δρ<τ,繼續(xù)執(zhí)行step 3。 綜上所述,本文提出的RASVDD離群檢測(cè)算法如表3所示。 為了驗(yàn)證本文提出的RASVDD算法性能,使用國(guó)際通用的無(wú)線傳感網(wǎng)絡(luò)數(shù)據(jù)集Intel Berkeley及SensorScope System完成了仿真實(shí)驗(yàn)。實(shí)驗(yàn)是在Intel(R)corei3雙核CPU,主頻3.6 GHz,內(nèi)存4G,操作系統(tǒng)Window 7環(huán)境下進(jìn)行的,編程語(yǔ)言采用MATLAB 2014a。在相同的實(shí)驗(yàn)環(huán)境下,分別實(shí)現(xiàn)了RASVDD算法、基于SMO的SVDD算法(以下簡(jiǎn)稱(chēng)為SVDD),以及Zhang[7]的AOD算法,并進(jìn)行了實(shí)驗(yàn)結(jié)果的比較。 3.1 數(shù)據(jù)集 Intel Berkeley數(shù)據(jù)集來(lái)自于部署在Intel Berkeley實(shí)驗(yàn)室中的無(wú)線傳感器網(wǎng)絡(luò),該網(wǎng)絡(luò)包含54個(gè)MICA2傳感器節(jié)點(diǎn),采樣周期為30 s,運(yùn)行周期為2004年2月28日到2004年4月5日,每個(gè)節(jié)點(diǎn)采集的數(shù)據(jù)包括溫度(Temperature)、濕度(Humidity)、光照(light)及電壓(voltage)4個(gè)屬性。本文選取1號(hào)傳感器節(jié)點(diǎn)2004年2月28日到2004年3月2日全天的溫度、濕度采樣數(shù)據(jù)作為本實(shí)驗(yàn)數(shù)據(jù)集。SensorScope System數(shù)據(jù)集來(lái)自于部署在瑞士和意大利之間Grand-St-Bernard山峰的2 400 m處的無(wú)線傳感器網(wǎng)絡(luò),數(shù)據(jù)從2007年9月開(kāi)始采集。每個(gè)節(jié)點(diǎn)采集的數(shù)據(jù)包括環(huán)境溫度(Ambient Temperature)、地表溫度(Surface Temperature)、日光照射(Solar Radiation)、相對(duì)濕度(Relative Humidity)等屬性。本文選取2號(hào)傳感器節(jié)點(diǎn)2007年9月15日到2007年9月18日的環(huán)境溫度和地表溫度采樣數(shù)據(jù)作為實(shí)驗(yàn)數(shù)據(jù)集。表4列出了本文實(shí)驗(yàn)所用的4個(gè)數(shù)據(jù)集。 表4 實(shí)驗(yàn)所用數(shù)據(jù)集 3.2 性能評(píng)價(jià)指標(biāo) 對(duì)于二分類(lèi)問(wèn)題,可將樣本根據(jù)其真實(shí)類(lèi)別和決策模型檢測(cè)類(lèi)別的組合劃分成真正例(true positive,TP)、假正例(false positive,FP)、真反例(true negative,TN)、假反例(false negative,FN)4種情形,其可用“混淆矩陣”來(lái)說(shuō)明[19],如表5所示。 表5 分類(lèi)結(jié)果混淆矩陣 本文利用TPR(True Positive Rate)、TNR(True Negative Rate)、FPR(False Positive Rate)、FNR(False Negative Rate)作為衡量著指標(biāo),其計(jì)算公式如下: (16) (17) (18) (19) 3.3 約簡(jiǎn)策略的對(duì)比試驗(yàn) 為驗(yàn)證本文提出的基于馬氏距離標(biāo)準(zhǔn)的約簡(jiǎn)策略在決策模型訓(xùn)練時(shí)間上的性能,分別使用SVDD算法和RASVDD算法在不同規(guī)模數(shù)據(jù)集上做訓(xùn)練,并用訓(xùn)練時(shí)間即決策模型形成所用時(shí)間作為衡量指標(biāo),結(jié)果如圖4所示。由圖4可得,RASVDD算法在訓(xùn)練時(shí)間方面有明顯優(yōu)勢(shì),相對(duì)SVDD算法訓(xùn)練時(shí)間總體減少20%以上,在訓(xùn)練數(shù)據(jù)樣本增多時(shí),優(yōu)勢(shì)更為明顯。這是由于RASVDD算法利用馬氏距離的標(biāo)準(zhǔn)有效地刪減了訓(xùn)練集中與決策無(wú)關(guān)的冗余數(shù)據(jù),故RASVDD算法在訓(xùn)練決策模型時(shí),省去了訓(xùn)練冗余數(shù)據(jù)的時(shí)間,提高了決策模型的訓(xùn)練速度。 圖4 SVDD算法和RASVDD算法在不同規(guī)模訓(xùn)練集上的訓(xùn)練時(shí)間 3.4 離群檢測(cè)算法性能的對(duì)比試驗(yàn) 為驗(yàn)證RASVDD算法性能,分別在上述4個(gè)數(shù)據(jù)集上對(duì)算法進(jìn)行對(duì)比,由表6~表9可得,RASVDD算法考慮了自然環(huán)境的多變性,采用基于數(shù)據(jù)分布密度的自適應(yīng)檢測(cè)機(jī)制,在數(shù)據(jù)流發(fā)生變化時(shí)通過(guò)更新準(zhǔn)則及時(shí)有效地更新了決策模型,其TPR平均達(dá)98.52%,FPR平均僅為0.61%,而SVDD算法的TPR平均僅為59.68%,而FPR平均高達(dá)35.8%,由此可得RASVDD有效改善了SVDD不能自適應(yīng)更新的問(wèn)題,表現(xiàn)出了優(yōu)于SVDD的良好檢測(cè)性能。由表6~表8可得AOD算法在數(shù)據(jù)集Ⅰ,Ⅱ,Ⅲ上均表現(xiàn)出良好的檢測(cè)性能,TPR達(dá)97%以上,但由表9可得其在數(shù)據(jù)集Ⅳ上TPR大幅下降,僅為18%,這是由于數(shù)據(jù)集Ⅳ在數(shù)據(jù)流未出現(xiàn)離群點(diǎn)前數(shù)據(jù)分布便發(fā)生了變化,AOD算法更新準(zhǔn)則沒(méi)有檢測(cè)到數(shù)據(jù)流變化未及時(shí)更新決策模型,而RASVDD算法更新準(zhǔn)則是基于數(shù)據(jù)分布密度,故在數(shù)據(jù)集Ⅳ上也保持了良好的檢測(cè)性能。綜上,對(duì)比AOD算法和SVDD算法,RASVDD具有更好的離群檢測(cè)性能。 表6 IBRL_1數(shù)據(jù)集性能測(cè)試結(jié)果 表7 SensorScope_1數(shù)據(jù)集下性能測(cè)試結(jié)果 表8 SensorScope_2數(shù)據(jù)集下性能測(cè)試結(jié)果 表9 IBRL_2數(shù)據(jù)集下性能測(cè)試結(jié)果 圖5 SVDD算法和RASVDD算法的ROC曲線 圖5為ROC(Receiver Operating Characteristic)曲線,其縱軸為T(mén)PR,該值越高越好,橫軸為FPR,該值越低越好。這兩個(gè)指標(biāo)相互制約,若算法對(duì)離群數(shù)據(jù)敏感,則TPR會(huì)較高,但FPR也會(huì)相應(yīng)地升高。在理想情況下,當(dāng)所有的離群樣本均被檢測(cè)為離群,正常樣本均被檢測(cè)為正常,此時(shí)TPR為1,FPR為0;在TPR達(dá)到1時(shí),算法對(duì)離群數(shù)據(jù)靈敏性的提升只能導(dǎo)致正常樣本被檢測(cè)為離群,此時(shí)TPR為1,FPR不斷增大;在最極端情況下,全部樣本均被檢測(cè)為離群,此時(shí)TPR為1,FPR也為1。在對(duì)不同算法性能進(jìn)行比較時(shí)較為合理的判斷依據(jù)是比較ROC曲線下的面積[19],即AUC(Area Under ROC Curve)。圖5為SVDD和RASVDD的ROC曲線,由圖可以明顯看出SVDD的ROC曲線被RASVDD的曲線完全包住,因此RASVDD擁有更大的AUC,故RASVDD的性能優(yōu)于SVDD。 圖6給出了訓(xùn)練集樣本取值為[100,300,500,700,900,1100]時(shí),RASVDD、SVDD訓(xùn)練集樣本數(shù)和TPR、FPR的關(guān)系。 圖6 訓(xùn)練集樣本數(shù)對(duì)檢測(cè)算法性能的影響 從圖6(a)可以看出,SVDD的TPR存在很大的波動(dòng)性,隨著樣本數(shù)的增加,其TPR會(huì)逐漸降低。這是由于在訓(xùn)練樣本較多時(shí),SVDD算法將訓(xùn)練集內(nèi)的數(shù)據(jù)全部判斷為正常。例如:訓(xùn)練集樣本包含全天所有時(shí)刻的數(shù)據(jù),進(jìn)行在線檢測(cè)時(shí),若在凌晨時(shí)刻出現(xiàn)正午時(shí)刻的數(shù)據(jù),其應(yīng)該被判斷為離群。但由于SVDD決策模型中含有全天候的數(shù)據(jù),而且檢測(cè)算法沒(méi)有使用自適應(yīng)更新機(jī)制,SVDD算法通常會(huì)將該離群數(shù)據(jù)判斷為正常數(shù)據(jù),即造成誤判,故在樣本數(shù)增加時(shí),其TPR會(huì)降低,而RASVDD根據(jù)數(shù)據(jù)分布密度自適應(yīng)更新了決策模型,故其TPR對(duì)訓(xùn)練樣本數(shù)變化不敏感。從圖6(b)可得SVDD在訓(xùn)練集樣本小于300時(shí)FPR高達(dá)45%以上,而RASVDD的FPR始終低于20%。這是由于在訓(xùn)練集樣本較少時(shí),SVDD算法將訓(xùn)練集以外的數(shù)據(jù)全部判斷為離群點(diǎn)。例如:訓(xùn)練集中只含有凌晨時(shí)間段的數(shù)據(jù),SVDD決策模型會(huì)將正午時(shí)刻的正常數(shù)據(jù)全部判斷為離群點(diǎn),而RASVDD更新準(zhǔn)則會(huì)根據(jù)數(shù)據(jù)分布密度的變化情況,及時(shí)更新決策模型,所以訓(xùn)練集樣本數(shù)的變化對(duì)RASVDD的FPR影響較小。 本文針對(duì)無(wú)線傳感網(wǎng)絡(luò)離群檢測(cè)提出了RASVDD算法,其主要特點(diǎn)有:利用基于馬氏距離標(biāo)準(zhǔn)的方法對(duì)訓(xùn)練數(shù)據(jù)集進(jìn)行約簡(jiǎn),刪減了與決策無(wú)關(guān)的數(shù)據(jù)樣本,使訓(xùn)練時(shí)間減少的前提下,避免了準(zhǔn)確率的損失;針對(duì)無(wú)線傳感網(wǎng)絡(luò)數(shù)據(jù)流會(huì)隨時(shí)間發(fā)生不定變化,本文使用了基于數(shù)據(jù)分布密度的自適應(yīng)決策模型更新機(jī)制,使決策模型隨數(shù)據(jù)流變化自適應(yīng)更新,提高了離群檢測(cè)算法的準(zhǔn)確率。在真實(shí)數(shù)據(jù)集下的仿真實(shí)驗(yàn)證明了RASVDD與以往同類(lèi)算法相比,對(duì)無(wú)線傳感網(wǎng)絡(luò)離群檢測(cè)有更好的分類(lèi)效果。本文算法是針對(duì)非均勻部署的低密度無(wú)線傳感網(wǎng)絡(luò)而設(shè)計(jì)的,著重利用節(jié)點(diǎn)數(shù)據(jù)流自身的時(shí)間相關(guān)性進(jìn)行離群檢測(cè)。在今后的算法研究中將考慮同時(shí)利用節(jié)點(diǎn)間的時(shí)空相關(guān)性,以便進(jìn)一步提高檢測(cè)精度,并降低算法復(fù)雜度。 [1] Zhang Y,Meratnia N,Havinga P. Outlier Detection Techniques for Wireless Sensor Networks:A Survey[J]. IEEE Communications Surveys and Tutorials,2010,12(2):159-170. [2] 單亞峰,湯月,任仁,等. 基于鄰域粗糙集與支持向量極端學(xué)習(xí)機(jī)的瓦斯傳感器故障診斷[J]. 傳感技術(shù)學(xué)報(bào),2016,29(9):1400-1404. [3] Chandola V,Banerjee A,Kumar V. Anomaly Detection:A Survey[J]. ACM Computing Surveys,2009,41(3):1-58. [4] Zhang Y,Hamm N A S,Meratnia N,et al. Statistics-Based Outlier Detection for Wireless Sensor Networks[J]. International Journal of Geographical Information Science,2012,26(8):1373-1392. [5] 任倩倩,李建中,程思瑤. 無(wú)線傳感器網(wǎng)絡(luò)中可容錯(cuò)的事件監(jiān)測(cè)算法[J]. 計(jì)算機(jī)學(xué)報(bào),2012,35(3):581-590. [6] Zhang Y,Meratnia N,Havinga P J M. Distributed Online Outlier Detection in Wireless Sensor Networks Using Ellipsoidal Support Vector Machine[J]. Ad Hoc Networks,2013,11(3):1062-1074. [7] Zhang Y,Meratnia N,Havinga P J M. Ensuring High Sensor Data Quality Through Use of Online Outlier Detection Techniques[J]. International Journal of Sensor Networks,2010,7(3):141-151. [8] Tax D M J,Duin R P W. Support Vector Domain Description[J]. Pattern Recognition Letters,1999,20(11-13):1191-1199. [9] Tax D M J,Duin R P W. Support Vector Data Description[J]. Machine Learning,2004,54(1):45-66. [10] 孫文柱,曲建嶺,袁濤,等. 基于改進(jìn)SVDD的飛參數(shù)據(jù)新異檢測(cè)方法[J]. 儀器儀表學(xué)報(bào),2014,35(4):932-939. [11] Hu C,Zhou B,Hu J. Fast Support Vector Data Description Training Using Edge Detection on Large Datasets[C]//International Joint Conference on Neural Networks. IEEE,2014:2176-2182. [12] 梁錦錦,劉三陽(yáng),吳德. 一種約減支持向量域描述算法RSVDD[J]. 西安電子科技大學(xué)學(xué)報(bào)(自然科學(xué)版),2008,35(5):927-931. [13] 謝迎新,陳祥光,余向明,等. 基于快速SVDD的無(wú)線傳感器網(wǎng)絡(luò)Outlier檢測(cè)[J]. 儀器儀表學(xué)報(bào),2011,32(1):46-51. [14] Platt J C. Fast Training of Support Vector Machines Using Sequential Minimal Optimization[M]. MIT Press,1999:185-208. [15] Fan R E,Chen P H,Lin C J. Working Set Selection Using Second Order Information for Training Support Vector Machines[J]. Journal of Machine Learning Research,2005,6(4):1889-1918. [16] Liu Y H,Liu Y C,Chen Y J. Fast Support Vector Data Descriptions for Novelty Detection.[J]. IEEE Transactions on Neural Networks,2010,21(8):1296-313. [17] 周勝明,曲建嶺,高峰,等. 基于HE-SVDD的航空發(fā)動(dòng)機(jī)工作狀態(tài)識(shí)別[J]. 儀器儀表學(xué)報(bào),2016,37(2):308-315. [18] 金澈清,錢(qián)衛(wèi)寧,周傲英. 流數(shù)據(jù)分析與管理綜述[J]. 軟件學(xué)報(bào),2004,15(8):1172-1181. [19] 周志華. 機(jī)器學(xué)習(xí)[M]. 北京:清華大學(xué)出版社,2016:33-35. 魏暢(1993-),女,江南大學(xué)物聯(lián)網(wǎng)工程學(xué)院碩士研究生,主要研究方向?yàn)闊o(wú)線傳感網(wǎng)絡(luò)離群檢測(cè),weichang92@126.com; 李光輝(1970-),男,通信作者,教授,博士,博士生導(dǎo)師,主要研究方向?yàn)闊o(wú)線傳感器網(wǎng)絡(luò)、無(wú)損檢測(cè)技術(shù)等,ghli@jiangnan.edu.cn。 OutlierDetectioninWirelessSensorNetworksBasedonReductionStrategyandAdaptiveSVDD* WEIChang1,3,LIGuanghui1,2,3* (1.School of IoT Engineering,Jiangnan University,Wuxi Jiangsu 214122,China; 2.Jiangsu High Technology Research Key Laboratory for Wireless Sensor Networks,Nanjing 210003,China; 3.Research Center of IoT Technology Application Engineering(MOE),Wuxi Jiangsu 214122 China) Wireless sensor networks are often deployed in the harsh and unattended environment,and the sensor data loss or error usually happens for the sake of bad weather,hardware or software fault,energy dissipation or the adverse attack. Outlier detection of the sensor data streams is critical for improving the system’s availability. In this paper,an outlier detection method(RASVDD)based on the data reduction and adaptive SVDD is proposed. RASVDD uses the Mahalanobis distance criterion to reduce the data set and the training samples,and then the data distribution density criterion and the temporal correlation of data stream are applied to update the training model adaptively. The simulation results for the Intel Berkeley dataset and the SensorScope System dataset showed that,RASVDD had an average true positive rate of 98% and an average false positive rate of 1%,and reduced the model training time more than 20% compared to traditional SVDD. wireless sensor network;data reduction;SVDD;outlier detection;simulation 項(xiàng)目來(lái)源:國(guó)家自然科學(xué)基金項(xiàng)目(61472368,61174023);江蘇省重點(diǎn)研發(fā)計(jì)劃項(xiàng)目(BE2016627) 2017-03-19修改日期:2017-05-15 TP274.2 :A :1004-1699(2017)09-1388-08 10.3969/j.issn.1004-1699.2017.09.015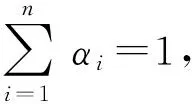
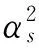
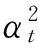
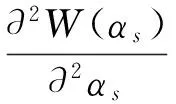
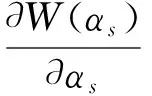
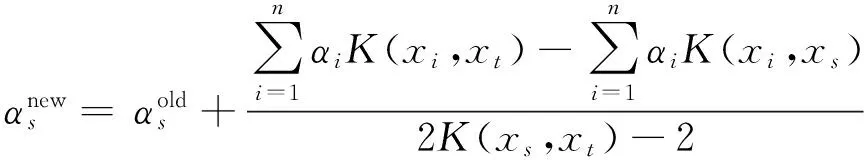
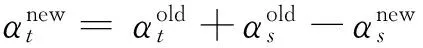
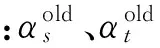
2 基于約簡(jiǎn)策略與自適應(yīng)SVDD的無(wú)線傳感網(wǎng)絡(luò)離群檢測(cè)方法
Σij=cov(Xi,Xj)=E[(Xi-μi)(Xj-μj)]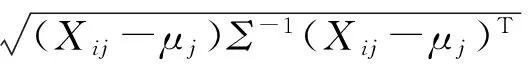

3 仿真結(jié)果及其分析

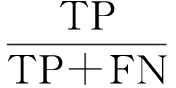
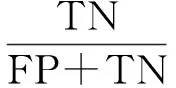
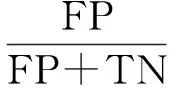
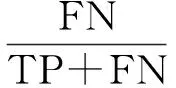
4 結(jié)論



