融合電磁超聲載波的聲發射傳播特性分析*

蔡智超,張 闖

(1.華東交通大學電氣與自動化工程學院,南昌 330013;2.河北工業大學電磁場與電器可靠性省部共建重點實驗室,天津 300130)

融合電磁超聲載波的聲發射傳播特性分析*

蔡智超1*,張 闖2

(1.華東交通大學電氣與自動化工程學院,南昌 330013;2.河北工業大學電磁場與電器可靠性省部共建重點實驗室,天津 300130)

電磁聲發射是通過對缺陷導電結構件施加非接觸式電磁載荷,進而激發聲發射應力波,并據此效應來進行構件無損檢測。本文針對電磁聲發射信號不適合較遠距離傳播問題,融合電磁超聲技術,實現對聲發射應力波的載波遠距離傳輸。文章首先從自由電子運動理論出發,從微觀層面上研究電流對金屬位錯激活能的影響,推導出定向漂移的自由電子與位錯碰撞時所產生的能量交換;其次搭建了融合電磁超聲載波的電磁聲發射有限元模型,分析了多個特征源激勵下的應力波傳播位移;最后利用希爾伯特黃變換方法對載波實驗信號進行了分析比較。本文通過對傳統的電磁聲發射激勵端研究、改進,提升電磁超聲對電磁聲發射應力波的傳輸特性,拓寬了電磁聲發射檢測的應用范圍。

電磁聲發射;電磁超聲;融合;載波;傳播特性

循環型失效是承壓型結構的主要失效模式,同時在加工以及制造過程中存在各類缺陷,在工況循環載荷作用下,極易產生疲勞裂紋進而影響整體結構的疲勞壽命,由此可能引發災難性的事故[1]。因此對于循環載荷作用下所含缺陷設備的安全性的檢測評估尤為重要。其中電磁聲發射技術使用局部的電磁激勵代替了聲發射傳統的整體加載,避免對完好區域造成損傷以及非檢測區域噪聲信號的干擾,可利用這一特性對特定區域的缺陷進行甄別。因此該方法對于萌生的疲勞裂紋、瞬時故障有較好的檢測能力[2-4],該方法兼顧聲發射對動態裂紋檢測的高效率以及電磁無損檢測的非接觸、無需耦合劑、惡劣環境下局部加載等獨特優勢。

然而,電磁聲發射檢測裂紋研究中存在兩個問題:一是電磁加載過程中應區分電磁激勵所產生的彈性超聲波與電磁聲發射應力波;二是電磁聲發射信號非常微弱,并不適合于遠距離傳輸,存在著未傳達至接收換能器時便已衰減的問題。因此為了傳輸、獲取、區分所評價結構件性能和缺陷狀態的聲發射信號,且保證原始信號的完整性,本文選擇融合電磁超聲載波的電磁聲發射方法,旨在探索融合檢測方式對疲勞損傷檢測的可行性。

融合電磁超聲載波的電磁聲發射源于傳統的聲-超聲技術[5-6],同樣也具備評估彌散缺陷分布以及材料力學性質變化等基礎應用能力,并且集電磁超聲和電磁聲發射技術特點于一身:如圖1所示,利用復合線圈在被測表面感應渦流,由于缺陷邊界的存在對表面渦流分布造成一定的影響,并在裂紋尖端處產生渦流集中效應,基于電致塑性效應將在該處激勵電磁聲發射信號;同樣基于電磁-結構耦合換能原理在電磁線圈正下方渦流區域也將產生振動的超聲彈性波[7]。因此,在同時激發超聲波與聲發射應力波兩種聲波的前提下,利用超聲波攜帶聲發射信號完成遠距離傳輸過程,提高聲波傳輸效率以實現對疲勞裂紋評估。

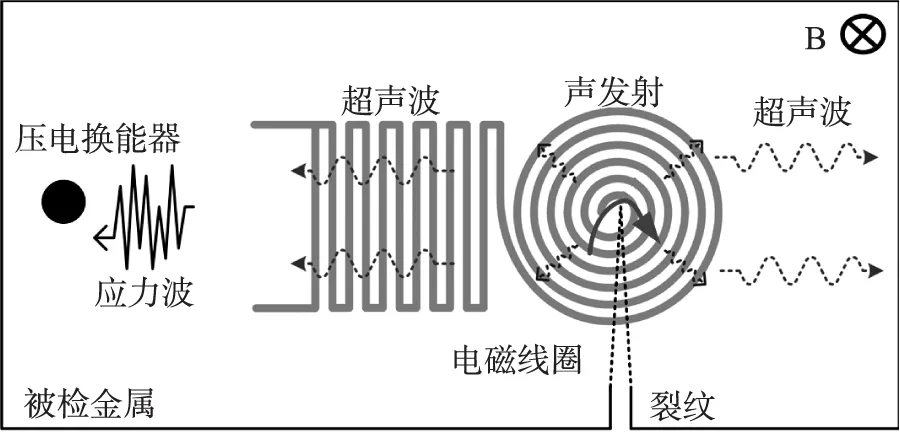
圖1 融合檢測中電磁聲發射模型圖

本文從自由電子理論出發分析電磁聲發射機理,利用有限元方法實現對電磁超聲載波過程比較、分析、計算試塊中聲波的傳播過程以及超聲波載波情況。制作含疲勞裂紋的損傷試件,設計了電磁檢測線圈及融合電磁超聲載波的電磁聲發射實驗,并基于希爾伯特黃方法對實驗過程中所采集到的應力波信號進行特征分析,探究不同頻率下超聲的載波效率等問題。

1 基于自由電子理論的電磁聲發射分析

瞬時高密度電流作為一種附加注入能量將對原子的隨機運動將產生影響,促進原子擴散能力,推動位錯運動(滑移、攀移),美國Conrad學者將定向運動電子與不規則原子排列產生的位錯作用情況定義為電子風力[8-9]。

在電子風力的作用下,位錯的自由端繞扎釘中心旋轉,直至位錯線方向與電流方向平行,此時電子風力對位錯的作用最小。漂移電子通過碰撞使得電子的自身能量轉移至位錯,并增強了位錯運動,即位錯運動與漂移電子運動方向有關,同樣外加靜磁場能對位錯運動方向產生影響。所以從自由電子層面研究有利于分析電磁加載對金屬位錯的具體影響,能更直觀地得出施加的電磁載荷參量與聲發射之間的關系。

導體晶體結構并非完美,或多或少會存在晶體缺陷、空位、位錯、雜質等,這些將散射漂移電子。常溫中原子依然存在熱運動,其將在晶格位置上下振動。漂移電子無法避免與這些振動的原子相碰撞,而被振動的晶格散射并做無規則隨機運動,即在無電場的情況下漂移電子在任何方向都不會顯示任何凈位移。如存在一個固定電場,漂移電子會與振動的原子突然碰撞并損失部分動能,但由于電場力的存在,其在圍繞固定方向上做加速運動,并不斷與該區域上的原子撞擊,這種電子傳遞的方式會使運動方向及能量發生改變,從而獲得與場強相關的穩定漂移速率,雖然運動路徑是曲折的,但在宏觀上表現為定向運動。

當電子受x方向電場Ex作用下的漂移速率vdx,假設該方向第i個漂移電子受電場作用在ti時刻與某一原子發生碰撞,碰撞后瞬時速度為uxi,在電場力作用下以加速度eEx/me經過(t-ti)時間,在t時刻產生的瞬時速率vxi為:

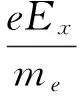
(1)

式中:e為單個電子電荷,me為單個電子質量。

式(1)是針對某一電子而言的速率分析,如若考慮總數為N個電子進行速率平均可得:

(2)

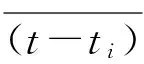
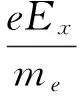
(3)

式中:μd=eτ/me為遷移率,作為電子常數,其與電子平均散射時間τ有直接的關系,晶格振動、晶體缺陷和雜質等的存在也會影響τ的變化。顯然針對于相同的材料而言,在結構不發生任何變化的情況,其遷移率是個恒定值。由式(3)可知電場強度越大,漂移速率也越大。

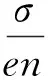
(4)

式中:n為導體內單位電子數目,d表示密度,Mst指代單位體積原子總質量,NA為單位體積原子個數。

導帶中電子平均速度u達到106m/s,因此在極高的工作電流(～107A/mm2)或電壓(～102kV/m)加載情況下,其引起的漂移速率遠小于電子的平均速度。所以當電場作用于一個導體時,實際上其平均速率并不受影響。電場的加載并不能改變電子平均速率,即加強電場幅值不能改變電子熱運動過程,從另外一個側面也就說明了焦耳熱效應在電致塑性過程中的作用極低。漂移電子與原子碰撞的激烈程度未變,電子所具有的動能并未發生明顯變化。

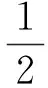
(5)

當漂移電子在其運動路徑上與晶體缺陷內大量位錯交互時,弛豫時間τ將變小,漂移電子會更為集聚,則單位時間內漂移電子與位錯區域中原子的碰撞幾率zE=1/τ將明顯增大。則單位時間內位錯區域從漂移電子中獲得的能量更為集中。

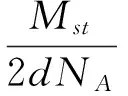
(6)

式中:PE?P=zW,z表示單位時間內每個自由電子與位錯碰撞的次數,P則代表了單位時間單個位錯從自由電子獲得的能量。式(6)中NE為單位時間撞擊位錯區域的電子濃度。

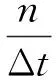
(7)

由式(7)可得電場的作用強度越大,其在單位時間內撞擊位錯區域的電子濃度就會越高。

因此在施加電場情況下,電子與構成位錯的原子相碰撞,位錯結構中的原子將獲得能量:瞬時高幅值電場加載,伴隨著原子在短時間內與大量漂移電子的撞擊,位錯原子將瞬間積累強大的能量。位錯原子所獲得集中的電子轉移的能量能夠克服勢壘障礙,促使位錯滑移。若形成晶格位錯的原子平均數為M,則在單位時間內電場產生的漂移電子作用于位錯的總能量為:

PT=MPE

(8)

式(8)為轉移至位錯的總能量,形成電磁加載后的激活能。因此基于經典自由電子理論可定性地給出電場作用強度與電磁聲發射的直接關系:①導體的遷移率越大,更易實現漂移電子的運動,電子在移動過程中與位錯的碰撞頻率將增大,傳遞給位錯的能量就越大;②電場實現了漂移電子的定向移動,使得電子的運動路徑與位錯發生交叉;漂移電子的集聚,實現大量數目漂移電子與位錯之間的能量轉換;③增強電場推動電子的漂移速率以改變單位時間內作用于位錯的數目。同時晶格位錯的數目增加也會縮短弛豫時間,增加每單位時間的碰撞幾率;④電場的加載時間持續必然體現位錯能量的積累,這個期間產生焦耳熱現象將增強原子自身的振動頻率,改變弛豫時間,進而提高轉換能量的累積。

故在電磁聲發射過程中,源于能量轉換的電子風力及長時間加載的焦耳熱效應是相互關聯,并且與缺陷屬性、電磁加載條件等緊密相關。

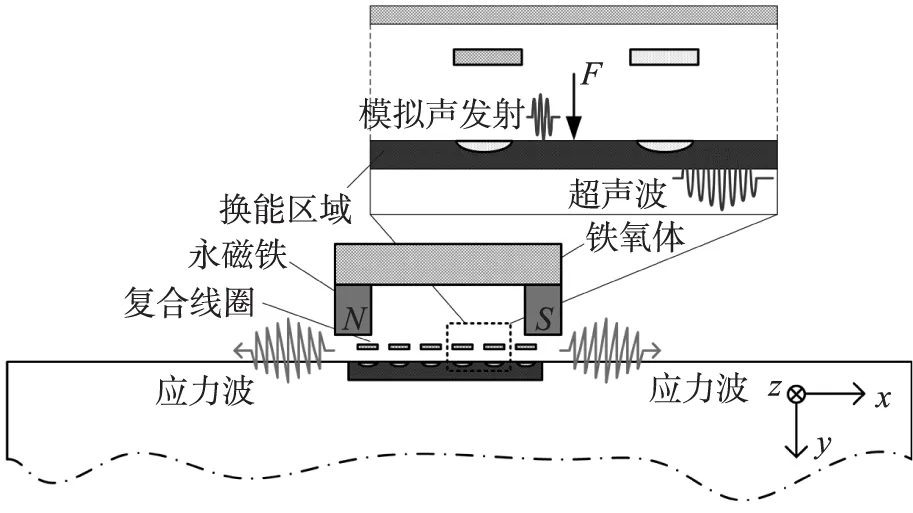
圖2 融合檢測中電磁聲發射有限元模型

2 融合檢測聲場有限元計算

融合檢測中電磁聲發射檢測有限元模型,如圖2所示,U型永磁鐵兩極頭使用型號為N35的釹鐵硼,其剩磁為y軸方向1.2 T,極頭中間放置鐵氧體。選擇500 kHz控制頻率復合線圈如圖1所示,電磁線圈通以持續時間為87.5 μs的500 kHz正弦周期50 A電流,交變磁場以及靜磁場共同作用所產生的洛倫茲力設定為結構場的體力載荷,對金屬表面固定點施加特定函數作用力以實現電磁聲發射載荷的模擬。

真實電磁聲發射信號具有中心頻率、較寬的信號頻帶以及極短的持續時間等特點。因此,利用高斯窗函數調制掃頻信號進行近似描述,其控制方程為:

(9)

式中:A為信號幅值,fs為信號下限截止頻率,B為信號頻帶寬度,T為信號瞬時持續時間。針對此模型設計模擬聲發射信號fs=275 kHz、B=50 kHz,即信號頻率范圍為275 kHz～325 kHz,其中心頻率為300 kHz,持續時間T=87.5 μs,寬帶系數α=2×109s-2,時間系數τ=40 μs,下限截止頻率修正系數β=0.73,信號頻帶寬度修正系數η=0.25。模擬電磁聲發射函數波形圖及頻譜圖如圖3、圖4所示。

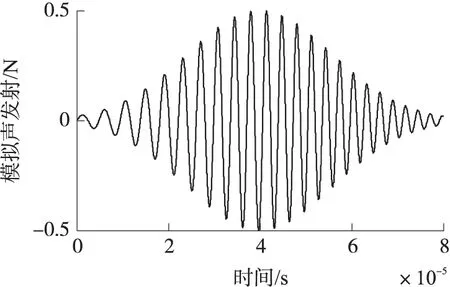
圖3 電磁聲發射源函數F(t)

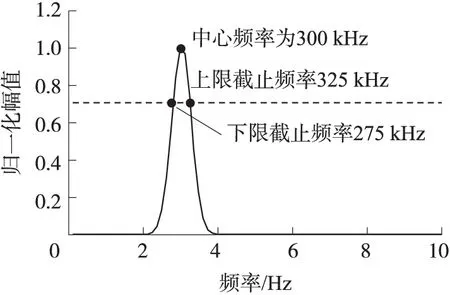
圖4 電磁聲發射源函數F(t)頻譜

在換能區域(趨膚區域)對網格進行三層以上的網格剖分,在聲場傳播區域最大網格尺寸設定為表面波波長的1/4,以此保證求解計算的準確性和穩定性。

經過對有限元模型瞬態求解之后,電磁線圈所產生的超聲波面外位移如圖5所示。隨著傳播時間的增加,表面波位移衰減較慢,而體波位移衰減較快。

2.1 聲波位移分析

為分析應力波的傳播效果,對比3種激勵源,如表1所示。可以求解距離發射復合線圈150 mm質點處應力波產生的聲波面外位移分量OP(Out-Plane Displacement)和面內位移分量IP(In-Plane displacement)。該處質點位移包括微弱的橫波成份和豐富的表面波成份,并且表面波IP比表面波OP相位超前π/2。

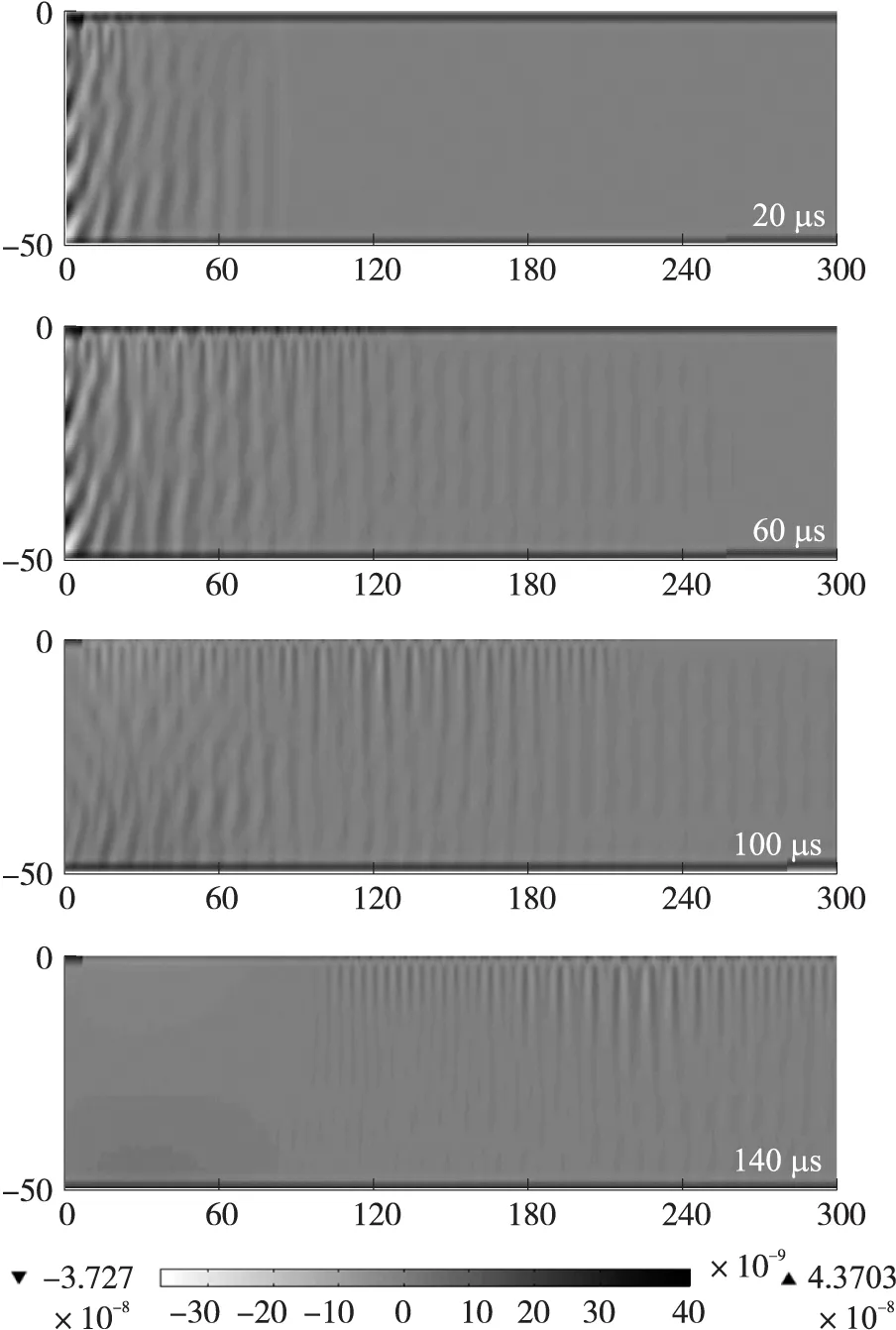
圖5 不同時刻鋁板中聲波面外位移分布圖

激勵源描述F(t)(簡稱F)聲場信號僅為聲發射F(t)+螺旋線圈產生的超聲波(簡稱FSC)聲場信號為聲發射與螺旋線圈產生的少量超聲波F(t)+電磁線圈產生的超聲波(簡稱FCC)聲場信號為聲發射與電磁線圈產生的豐富超聲波

“F”激勵源以模擬真實反演裂紋尖端的聲發射信號,其所產生的表面位移頻段為275 kHz～325 kHz,但是其位移最高幅值10-11mm,最為先進的聲發射換能器也僅能采集到10-12mm幅值的信號。但是所采集的聲發射信號將受噪聲干擾,同時初始、末尾兩端微弱的聲發射信號將不易采集,如圖6(a)所示。然而長距離的聲波傳輸嚴重影響聲發射信號特征的提取,降低聲發射頻帶寬度。

利用“FSC”來模擬傳統的電磁聲發射信號,其常由單獨的螺形線圈施以電磁載荷,然而該過程也將引入超聲彈性波,如圖6(c)、圖6(d)所示,但其引入的超聲幅值較低,與被載的聲發射信號幅值幾近相當,雖能提高應力波的傳播距離,實現部分的載波效應,但所采集到聲波依然十分微弱,載波效果不顯著。對于電磁線圈激勵,由于其比傳統的電磁聲發射激勵線圈增加了蛇形側“FCC”,線圈結構如圖9所示,因此這將產生豐富的指向性超聲波,其IP及OP將接近到10-10mm,如圖6(e)、圖6(f)所示,因此增加蛇形側的電磁線圈能更好的提高載波效率。

圖6 固定點的面內及面外位移及FFT分解

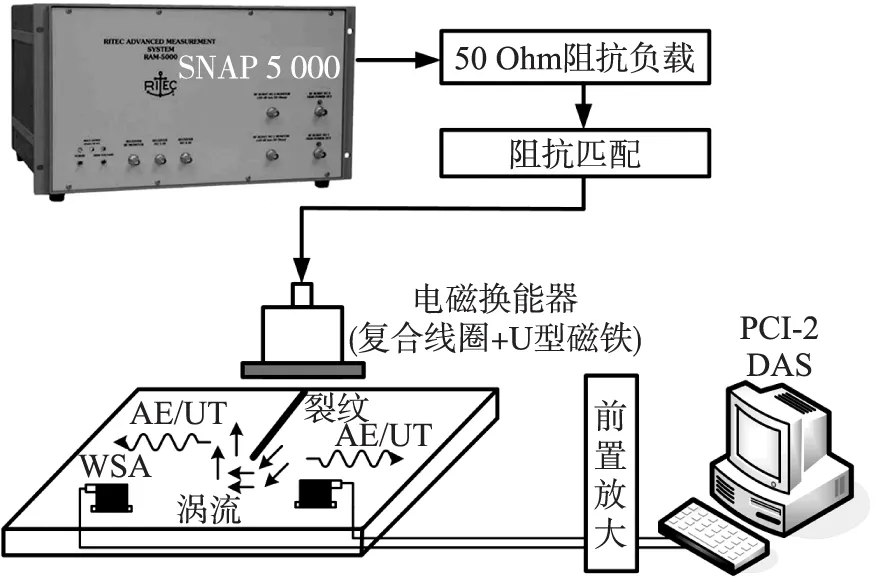
圖7 實驗系統原理框圖

3 電磁聲發射檢測實驗研究及信號分析

圖8 含疲勞裂紋的損傷試件

復合檢測實驗系統如圖7所示。電磁換能器為復合線圈與U形永磁體組合。傳統鋁板的聲發射集中于0～400 kHz,將激勵電流頻率選擇在500 kHz～1 000 kHz之間,從頻譜上以區別電磁聲發射信號與電磁超聲信號。試件為0.20 m×0.20 m×0.02 m的6061鋁塊,其中鋁塊邊緣通過線切割制作50 mm預制裂紋,經施加10 kN疲勞載荷,制作長約58 mm的疲勞裂紋,如圖8所示。

電磁線圈設計如圖9所示,螺旋側均采用線寬0.5 mm、線高0.035 mm、線間距0.3 mm;蛇形側采用線寬0.1 mm、線高0.035 mm,線間距可變以滿足兩相鄰線圈所通入電流相位相差π,滿足相長干涉疊加條件[7]。復合線圈采用柔性印刷電路板制作,減少提離距離以增大電磁載荷效率。

圖9 EMAE換能線圈

以圖9(f)電磁線圈為例,通以f=650 kHz的激勵電流。采集的時域信號波形如圖10(a)所示,所檢測信號在時域上由連續的聲波組成,在聲波前半段波包幅值變化較大,而聲波后半段波包幅值相對平穩。對該時域信號進行HHT變換求得邊際譜如圖10(b)所示,在650 kHz頻段附近的聲波信號最為強烈,即為電磁-結構換能所產生的超聲彈性波為主要貢獻,而在50 kHz～150 kHz以及350 kHz～450 kHz低頻段所呈現幅值較低、特征頻段突出等特點,即為電磁聲發射應力波信號為主要貢獻。

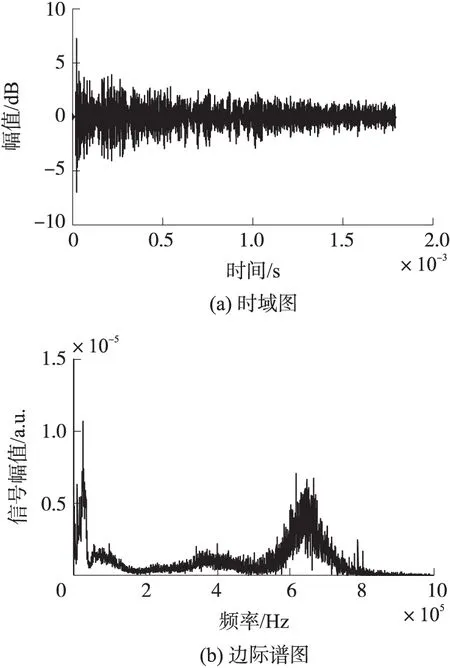
圖10 實驗特征信號

文獻[10]表明水平磁場下電磁聲發射隨著頻率變化所產生的總能量保持一致,對于相同電流幅值下不同頻率的激發其產生的聲發射特性差異并不顯著,即利用U型磁鐵作為水平磁場激勵,便可視其產生的電磁聲發射信號為恒定的聲波信號。

因此需對已采集的應力波信號進行超聲波濾波處理,給定原始信號一個500 kHz的低通濾波,再進行特定的信號處理方法:希爾伯特黃HHT(Hilbert-Huang)變換方法對非線性、非平穩信號的聲發射信號具有良好的處理能力,能夠自適應的時頻分解并增強了時頻集聚性,降低頻譜能量泄露的同時提高了時頻分辨率[11-13]。通過希爾伯特黃變換所求解各個本征模態函數IMF分量所占的不同的能量值:

(10)

式中:n表示為電磁聲發射信號的長度,該值是由采樣長度與預觸發值有關,ci(k)代表第i個IMF分量中的第k個元素,每個IMF分量的能量比值為:

Pi=Ei/Et

(11)

式中:Et表示IMF分量的總能量,即為各個Ei之和。

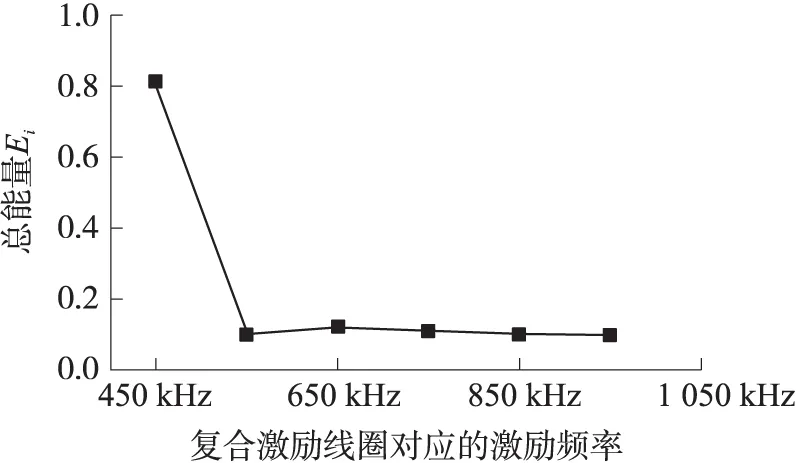
圖11 不同激勵頻率下應力波總能量

按式(11)求解各控制頻率線圈激發的聲發射信號的總能量Et。如11所示,當對所有設計頻段的電磁線圈進行激勵如圖9所示,圖9(d)電磁線圈產生的總能量明顯高于其他激勵線圈所產生的能量,這是由于450 kHz激勵線圈所產生的彈性波頻率與聲發射特征頻率發生重合,該部分的彈性波并未通過低通濾波器濾除,同時其頻率混疊將影響聲發射信號特征分析,因此該頻段并不適用于作為載波頻段。本文針對550 kHz～950 kHz頻率的電磁激勵所采集到的應力波信號進行分析,先濾除500 kHz以上彈性超聲波再對聲發射應力波進行分析。

通過希爾伯特黃計算可得計算可知信號中95%以上的能量集中于IMF1～IMF 5分量,表2為各個IMF分量對應的頻率范圍。

表2 IMF分量頻帶范圍

如圖12所示,不同的彈性超聲波下IMF1分量的Ei值呈相對上升趨勢,而其他分量的Ei值趨勢并不是十分顯著。同樣如圖13所示,IMF1分量的Pi值呈相對上升趨勢,而其他分量的Pi值變化范圍在0.05～0.30之間。即特征頻段IMF1受載波頻率變化最為顯著。

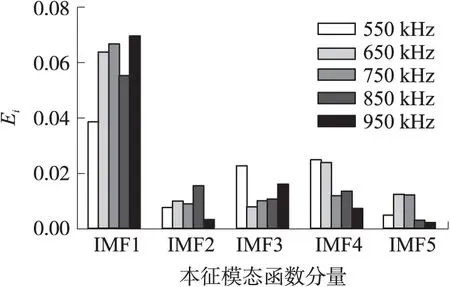
圖12 不同本征模態函數下Ei值情況

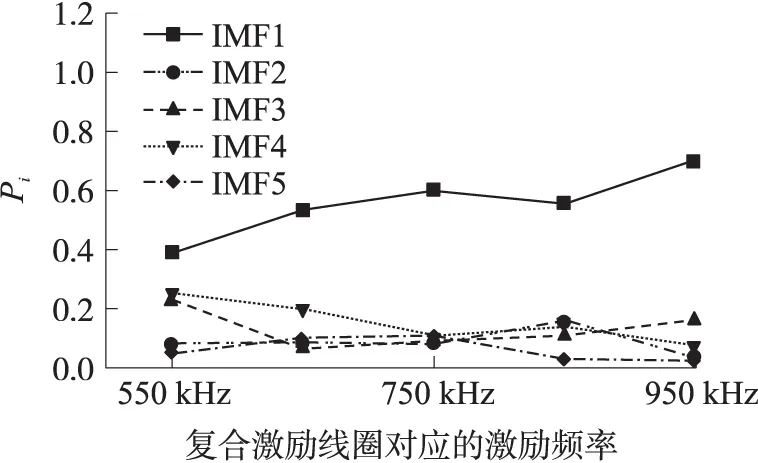
圖13 不同本征模態函數下Pi值情況

通過對比分析可以得出:當超聲載波與電磁聲發射特殊頻段相近時,載波效率較低;當載波與電磁聲發射特殊頻段存在一定頻率差時,載波效率較好。這是由于當載波頻段與聲發射特殊頻段相近時,易發生波速混疊,不適合加載聲發射信號遠距離傳輸。

5 結論

對融合電磁超聲載波的電磁聲發射技術進行理論、仿真、實驗方面的研究,主要結論如下:①定向電子的自由移動,通過動能的注入激活裂紋尖端位錯的運動,實現自由電子與位錯之間的能量交換,進而實現位錯集聚最為明顯的裂紋尖端位錯移動并釋放應力波信息;②電磁聲發射通過電磁線圈的激勵必然會引入彈性波,然而通過電磁換能線圈的改進,可在產生電磁聲發射的同時激勵出指向性超聲波這一特性,通過超聲載波能力實現對電磁聲發射應力波的遠距離傳輸。同時利用適合的頻段激勵、電磁線圈匹配、濾波等過程能夠在接收端實現兩種應力波的分離。

[1] 張伯君,業成,張忠政,等. 含裂紋缺陷氣瓶疲勞裂紋擴展及壽命預測[J]. 油氣儲運,2014,10:1061-1065.

[2] Finkel P,Godinez V. Electromagnetic Simulation of Ultrasonic Signal for Nondestructive Detection of Ferromagnetic Inclusions and Flaws[J]. IEEE Transactions on Magnetics,2004,40(4):2179-2181.

[3] 劉素貞,金亮,張闖,等. 電磁聲發射檢測技術的渦流激勵方法[J]. 電工技術學報,2012,27(7):153-159.

[4] 張曉濤,唐力偉,王平,等. 最小周期相關熵解卷積結合窄帶解調的軸承復合故障診斷研究[J]. 振動工程學報,2015,28(4):666-672.

[5] 陳振華,盧超,陸銘慧,等. 基于聲-超聲檢測的薄鋼板多焊點結構完整性評價技術[J]. 機械工程學報,2013,8(49):57-61.

[6] 尼濤. 時頻分析技術在聲-超聲檢測中的應用[J]. 聲學技術,2013,32(4):502-505.

[7] 范吉志,吳運新,石文澤,等. 電磁超聲換能器線圈設計與提高換能效率研究[J]. 傳感技術學報,2016,29(1):29-34.

[8] Lei Guana,Guoyi Tang,Paul K Chu. Recent Advances and Challenges in Electroplastic Manufacturing Processing of Metals[J]Journal of Materials Research,2010,25(7):1215-1224.

[9] Stephen D Antolovich,H Conrad. The Effects of Electric Currents and Fields on Deformation in Metals,Ceramics,and Ionic Materials:An Interpretive Survey[J]. Materials and Manufacturing Processes,2004,19(4):587-610.

[10] 蔡智超,劉素貞,張闖,等. 施加水平磁場下電磁聲發射與裂紋指向特征分析[J]. 振動與沖擊,2017,36(5):8-14.

[11] Seif E Hamdi,Alain Le Duff,Laurent Simon,et al. Acoustic Emission Pattern Recognition Approach Based on Hilbert-Huang Transform for Structural Health Monitoring in Polymer-Composite Materials[J]. Applied Acoustic,2013,74:746-757.

[12] Li Lin,Fulei Chu. HHT-Based AE Characteristics of Natural Fatigue Cracks in Rotating Shafts[J]. Mechanical Systems and Signal Processing,2012,26:181-189.

[13] 張建偉,朱良歡,江琦,等. 基于HHT的高壩泄流結構工作模態參數辨識[J]. 振動、測試與診斷,2015,35(4):777-783.

蔡智超(1989-),男,講師/博士后。主要從事工程電磁場、電磁無損檢測、電工理論新技術等研究。參與國家自然科學基金3項,《IEEE Transactions on applied Supercon-ductivity》雜志評審專家,在電磁超聲與聲發射復合檢測、換能器優化、非線性超聲等方面發表SCI/EI收錄十余篇,zccai@ecjtu.edu.cn。

PropagationCharacteristicsAnalysisofAcousticEmissionIntegratingElectromagneticUltrasonicCarrier*

CAIZhichao1*,ZHANGChuang2

(1.School of Electrical and Automation Engineering,East China Jiaotong University,Nanchang 330013,China; 2.Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology,Tianjin 300130,China)

Electromagnetic acoustic emission technology(EMAE)does nondestructive detection with the effect of contactless electromagnetic loading to generate a stress field stimulating stress waves from the defective conductive structure. The most significant problem faced by the metallic structural health monitoring method of EMAE is that EMAE signal is not suitable for long distance transmission,this problem was improved by integrating electromagnetic ultrasonic carrier method. Firstly,based on free electron theory,the mechanism of EMAE was studied at a microscopic level which based on the activation energy changed from the electrical current to mobile dislocations. Secondly,the difference of stress wave propagation characteristics under various electromagnetic stimulating conditions was researched by building finite element model. Finally,the comparison between the energy percentage intrinsic mode functions of carrier experiment was discussed by Hilbert-Huang transformation. The stress wave propagation characteristics of EMAE was improved by integrating electromagnetic ultrasonic method which based on the study and improvement of traditional exciting,and the range of EMAE application will be widened.

electromagnetically induced acoustic emission;electromagnetic acoustic;integration;carrier;propagation characteristic

項目來源:國家自然科學基金青年項目(51307043);江西省青年科學基金項目(20171BAB216035)

2017-02-03修改日期:2017-04-19

TB553

:A

:1004-1699(2017)09-1335-08

10.3969/j.issn.1004-1699.2017.09.006