房價非線性回歸模型及期權定價

馮 敬 海， 朱 駿 橋

( 大連理工大學 數學科學學院, 遼寧 大連 116024 )

房價非線性回歸模型及期權定價

馮 敬 海*， 朱 駿 橋

( 大連理工大學 數學科學學院, 遼寧 大連 116024 )

從宏微觀經濟學的角度出發，依照國家統計局網站的數據選取多個可能影響房地產價格的變量建立了全國房地產平均價格模型．運用R語言對數據進行了多元線性回歸分析、多元非線性回歸分析、相關性分析、多重共線性分析、嶺回歸分析等統計分析，得出房價的線性與非線性多個模型并進行了比較．結合隨機微分方程、實物期權等相關金融數學知識進行了房價模型的理論推導與實際估計，并對房價期權進行了定價．利用Matlab對模型進行了大量的模擬并得到較好結果．

實物期權；房價模型；隨機微分方程

0 引 言

房地產行業與我國經濟發展始終相互影響，它的狀況也間接反映了我國人民的生活水平．進入21世紀以來，我國經濟全面發展，房地產作為我國經濟的龍頭行業發展速度越來越快．國家政策始終在一定程度上影響著房地產價格．1990年5月，《中華人民共和國城鎮國有土地使用權出讓和轉讓暫行條例》的出臺，為土地使用權有償出讓提供了具體依據，為房地產市場形成和流轉房地產的建立奠定了基礎．2008年11月，4萬億元投資計劃的實施抵擋了國際金融危機的沖擊，阻止了GDP的下降，間接支撐了房地產行業的持續發展．諸如此類，數不勝數．近十年來，隨著經濟和教育水平的不斷提高，房地產價格快速增長的原因成為國內各大高校學者熱議的話題，與此相關的論文也層出不窮．影響房地產價格的因素較多，前人的論文所針對的方向各有不同，選取變量的依據大都為宏觀或微觀經濟學原理加之一定的主觀傾向，但依據的統計學方法如出一轍，得到的多元線性回歸模型都可以很好地解釋房地產價格的增長．

本文選取可能影響房地產價格的近10個變量進行統計學分析，數據來源于國家統計局網站．通過R語言[1]對多個變量與房地產平均銷售價格進行相關性分析、逐步回歸分析、非線性回歸分析、嶺估計等統計分析得到最優的擬合結果[2]．結合隨機微分方程的相關知識對其進行深入的探索，利用Matlab對隨機微分模型進行模擬，結合實物期權的相關知識對房價期權進行預測．

1 房價模型

1.1 房地產價格影響因素分析

經濟學對人的消費理論有深度的研究[3]．影響我國房地產平均銷售價格的主要因素有很多，本文選取了以下幾個因素作為自變量：

x1：商品房年度銷售面積，104m2；x2：廣義貨幣M2，即交易貨幣以及定期存款與儲蓄存款，億元；x3：年末總人口，萬人；x4：城鎮人口，萬人；x5：國民總收入，億元；x6：國內生產總值，億元；x7：人均國內生產總值，元；x8：城鎮居民家庭人均可支配收入，元；x9：城鎮居民家庭恩格爾系數，%

因變量y：全國商品房平均銷售價格，元．

1.2 數據歸一化

通過觀察原始數據表可以發現，這些數據不僅單位有差異，并且數量級相差比較大．為優化這種數據的處理，需對各個自變量進行歸一化處理．具體處理辦法如下：

之所以采用這種歸一化方法，是因為歸一化后所有數據均處于0～1，消除了單位不一致的缺點．本文中歸一化后的數據表示仍然采用歸一化之前的符號．

1.3 多元線性模型的建立與求解

根據這9個變量建立y的多元線性回歸模型：

y=β0+β1x1+β2x2+β3x3+β4x4+β5x5+β6x6+β7x7+β8x8+β9x9

首先，用R語言對數據進行擬合，step函數對其進行逐步回歸，得到結果如表1所示(擬合后發現x9的P值最大，隨后的擬合結果顯示x8的P值最大，故將這兩個變量剔除)．數據結果依然存在不夠顯著的情況，個別自變量與因變量之間正負相關關系不符合實際情況且可能存在多重共線性問題，故繼續選擇變量進行剔除，首先剔除不顯著的x5．國內生產總值x6應該與房價y呈正相關，隨后剔除變量x6，進而將不顯著的x2剔除．得到結果如表2所示．

表1 線性回歸模型數據初步擬合

表2 線性回歸模型數據擬合

這已經是一個比較好的結果，但是x4的系數β4仍然為負．城鎮居民人口越多，對房屋的需求量越大，導致房價變高．但是年末總人口x3的系數很大．考慮非城鎮人口即鄉村人口對y是否有影響，設x10=x3-x4，x10表示鄉村人口總數(單位：萬人)．擬合后得到結果：

y=-0.355 17+0.422 95x1+0.591 79x7- 0.739 56x9+2.631 38x10

該模型(模型1)與實際值對比如圖1所示，將t與y的數據點、預測估計曲線、預測區間曲線和置信區間曲線畫在一張圖上，效果更加直觀．

(a) 對比

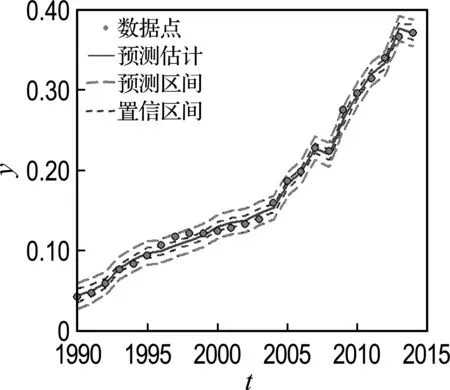
(b) 區間

圖1 模型1實際值與估計值對比

Fig.1 Comparison of actual and estimated values in Model 1

倘若不對變量x3和x4進行相減處理，由于x3和x4都是與人口相關的變量，數據中一定存在多重共線性．衡量數據是否存在多重共線性的一個重要指標就是矩陣XTX的條件數κ的大小，即

式中：X為數據標準化后的矩陣，λmin(XTX)和λmax(XTX)分別是矩陣XTX的最小特征值和最大特征值．條件數κ象征著XTX的特征值差異大小．利用R語言進行多重共線性分析得到矩陣XTX的最小特征值和最大特征值：λmin(XTX)=0.004 072 048 和λmax(XTX)=3.808 502，100<κ=935.281 088<1 000證明數據中存在中等程度的多重共線性．

采用嶺估計的方法解決多重共線性的問題，對于多元線性模型y=Xβ+ε，嶺估計的回歸系數定義為β(k)=(XTX+kI)-1XTy，公式中k為大于0的可選擇的參數，稱之為嶺參數．當k取不同值的時候，得到的估計結果也不同．若k=0，β(0)=(XTX)-1XTy即為普通的最小二乘估計．嶺跡圖如圖2所示．

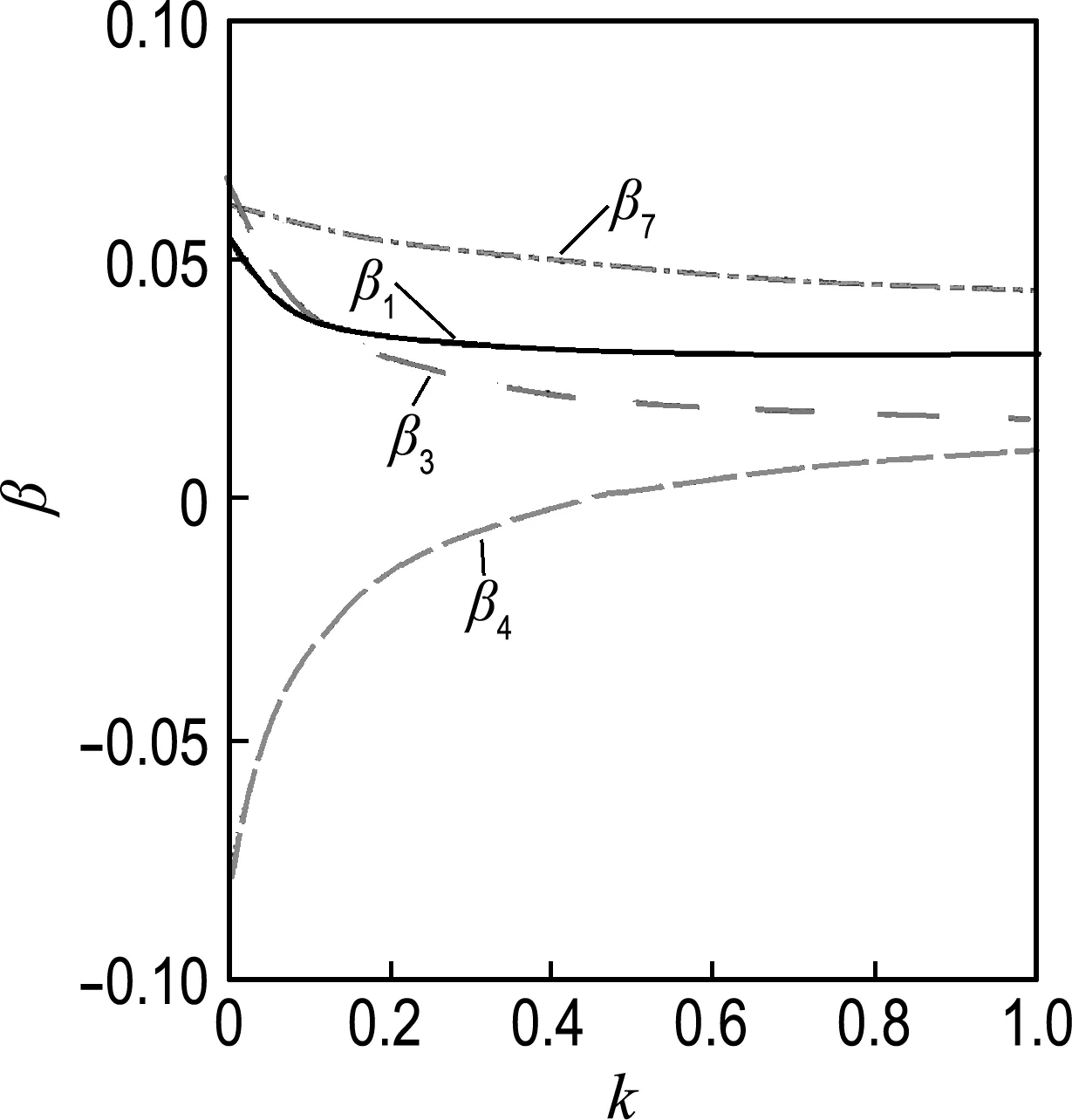
圖2 嶺跡圖

嶺回歸的R語言函數還提供了兩種確定嶺參數的方法，計算后得出L-W=0.004 400 138和HKB=0.002 495 606，但這兩種方法對于本問題得到的參數很不理想．所以，采用觀測嶺跡圖的方法，當k>0.4時，各變量的嶺跡趨于平穩，代入k=0.4后得到結果如表3所示．

表3 線性回歸模型數據擬合(k=0.4)

其中x4的系數β4依然為負，但與其他變量系數相比較小，暫且得到模型2如下：

y=-0.338 23+0.228 29x1+2.141 08x3- 0.032 59x4+0.377 24x7

該模型與實際值的對比圖如圖3所示．

1.4 非線性模型的建立

通過觀察數據發現，從1990年到2014年，大部分自變量及因變量y的值都顯著增大，以變量x2為例，其在25 a間擴大了近100倍．不難看出，x2隨著t的變化大致呈指數關系增長．假設它們之間的關系為x2=aebt，而后對等式兩側同時取對數，得到lnx2=lna+bt，對lnx2和t進行線性回歸，計算出結果a=-353.7，b=0.175 3．指數函數x2=aebt與實際值的對比圖4驗證了本文的猜想．

圖3 模型2實際值與估計值對比

圖4 x2=aebt與實際值

故假設房價與各變量之間的非線性模型為

lny=β0+β1lnx1+β2lnx2+β3lnx3+β4lnx4+β5lnx5+β6lnx6+β7lnx7+β8lnx8+β9lnx9+β10lnx10

由于變量x3、x4、x10均為與人口相關的變量，x6和x7均為與生產總值相關的變量，考慮多重共線性的問題，從這兩組變量中各取一個變量并結合其他變量進行擬合．利用R語言中lm函數與step函數進行擬合和變量篩選，并從多種組合中選取最優解．于是得到模型的解：

lny=-0.490 56+0.238 95lnx1+ 0.871 15lnx2+0.713 15lnx9+ 1.634 10lnx10

恩格爾系數越高，說明人民生活相對艱苦，間接導致房價降低．盡管我國提出了計劃生育等一系列控制人口增長速度的政策，我國總人口依然穩中有升，隨著鄉村人口的不斷向城鎮遷移，城鎮人口逐年增加．而城鎮房價顯著高于鄉村房價，故鄉村人口應與全國房地產平均價格呈現負相關．故推測數據中仍然存在多重共線性的可能．100<κ=442.329 6<1 000表示數據中存在中等程度的多重共線性．圖5為4個變量的嶺跡圖，選取k=1.7，各變量趨于平穩，得到多元非線性回歸方程如下，即模型3：

lny=0.287 60+0.202 96lnx1+ 0.392 11lnx2-0.026 91lnx9- 1.005 66lnx10

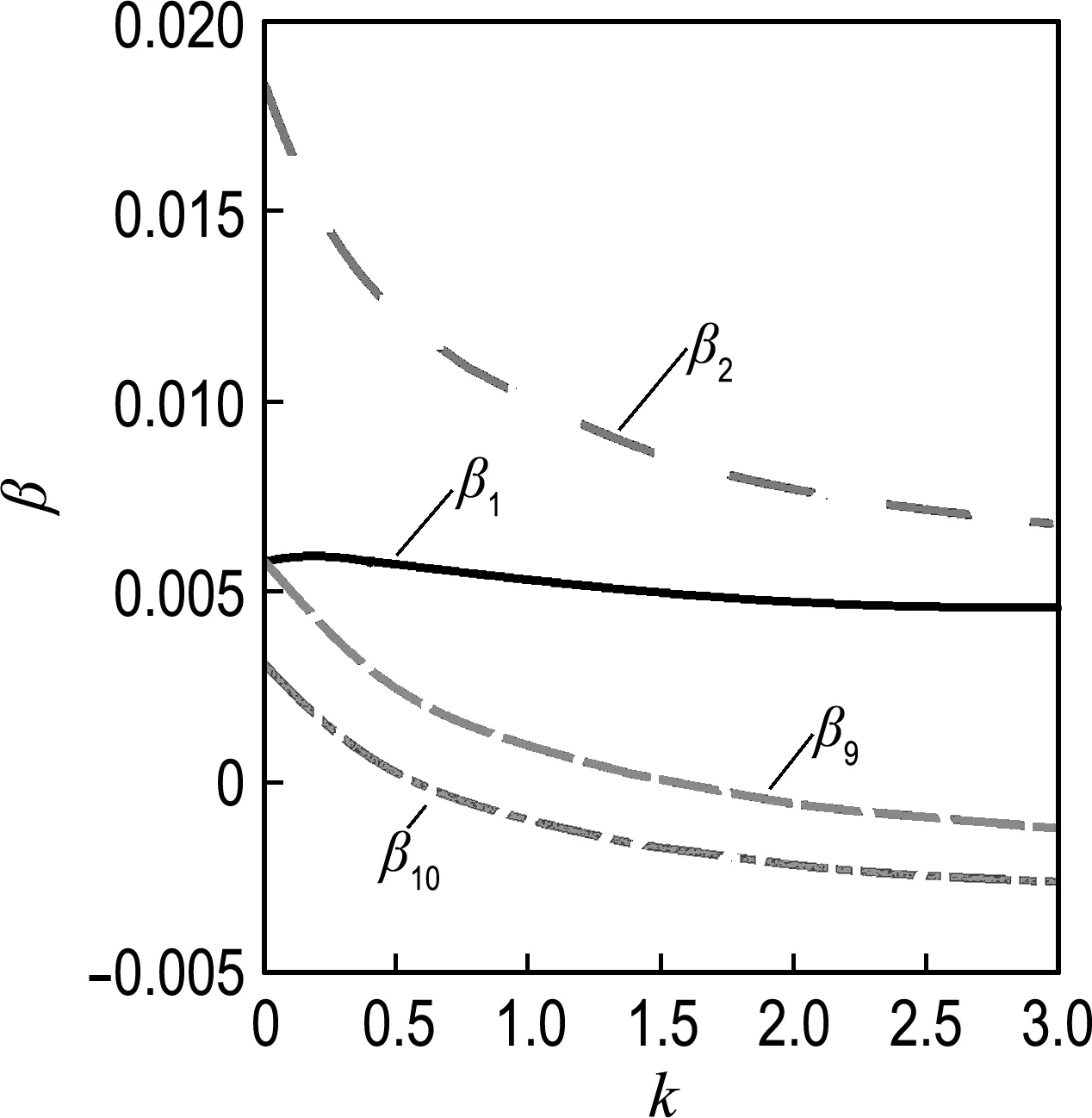
圖5 4個變量的嶺跡圖

估計值與實際值之間的對比圖如圖6所示．

圖6 模型3實際值與估計值對比

商品房年度銷售面積x1與廣義貨幣x2兩個變量與全國商品房平均銷售價格呈正相關．恩格爾系數x9、鄉村人口x10與全國商品房平均銷售價格呈負相關．其中，銷售面積之所以逐年增長，是由于我國人民生活水平提高、對大面積住房的需求等多種因素所導致的．我國現階段樓盤大戶型越來越多，并且大部分地區戶型越大房價越高．這說明市場需求量在增加，故銷售面積的增加導致了房價的增加．人口的增長也會導致房地產需求的增加，房價的提高在預期之內．但城鎮人口占全國人口比重較低，其生活水平卻過高，對于房價的影響雖然顯著，但卻不符合常理．故選用更能接近全國平均消費水平的鄉村人口作為變量研究，并且得到了很好的結果．

廣義貨幣的增加，說明人們的購買力越來越強，增加了市場需求，從而引發了房價的上漲．隨著生活水平的提高和時代的進步，人們的追求不僅限于房產，支配所擁有的財產的方式也越來越多．廣義貨幣的變動也是國家貨幣政策的間接體現，從屬于貨幣政策的利率政策、貸款政策以及公開市場業務都對廣義貨幣x2有著顯著的影響．該變量將國家政策間接、細致地體現于每一年的數據當中．模型中x2的系數β2較大也驗證了國家政策對房價有著一定程度的影響．

由于模型1中x10與y呈正相關，模型2依然存在多重共線性，故選擇模型3作為最終模型．

2 期權分析

2.1 模型及假設

根據上述模型得到：

假設Xi為幾何布朗運動，dXi(t)=μiXi(t)dt+σiXi(t)dBi(t)，初值為Xi(0)，其中{Bi(t),t≥0}為布朗運動，μi>0,σi>0，i=1,2,3,4，(B1(t)B2(t)B3(t)B4(t))T為4維相關布朗運動，且當i≠j時，相關系數ρij=ρBi(t)Bj(t),ρii=1．Y(t)表示全國商品房平均銷售價格,Xi表示影響Y(t)的變量．

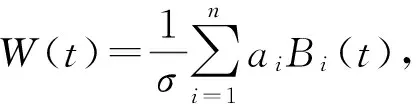
命題1在引理1的假設下，Y(t)為幾何布朗運動．

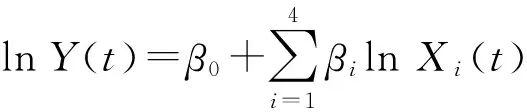
于是Y(t)=Y(0)eμt+σW(t)．

□

2.2 房地產價格的模擬

μ^i=1ΔtjlnFi(t)+12σ^2

其中

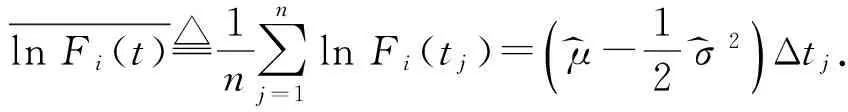
lnFi(t)1n∑nj=1lnFi(tj)=(μ^-12σ^2)Δtj.

代入歸一化后的數據，n=24，Δtj=1，j=1,2,…,

最終計算得出μ=0.010 657，σ=0.006 993，得到關于Y(t)的隨機微分方程：

dY(t)=0.010 657Y(t)dt+0.006 993Y(t)dB(t)

用Matlab軟件模擬計算100 000次并取均值，發現模擬結果較好(圖7)．其中1998年前后國際金融危機導致的房價增速緩慢輕微影響了擬合結果．

圖7 隨機微分模型的實際值與估計值對比

2.3 期權定價

設Y(0)為0時刻的房價，Y(t)為t時刻的房價，K為敲定價格，買入歐式看漲期權，收益(Y(t)-K)+，用C(t,Y(t))表示t時刻的期權[5]價值(t

首先考慮對沖思想，假設某人以全國房地產平均價格Y(t)購買了Δt處房產，并將剩余的資金存入銀行，則得到如下資產組合：

dΠt=ΔtdY(t)+r(Xt-ΔtY(t))dt

根據本文假設及引理1的證明可知，全國房地產平均價格滿足如下隨機微分方程：

由期權定價基本定理[6]得

其中t∈[0,T]，Y(t)≥0．該方程即為Black-Scholes-Merton方程．假設該期權為歐式期權，則終值條件C(T,Y(t))=(Y(t)-K)+．Black-Scholes-Merton方程的解為

C(t,Y(t))=Y(t)N(d+(T-t,Y(t)))-Ke-r(T-t)N(d-(T-t,Y(t)))； 0≤t0

其中N是N(0,1)的分布函數，其中

3 結 語

本文所得的3個房地產價格模型各有各的特點，且擬合效果均達到預期效果，最終選取多元非線性模型作為最佳選擇．對房價這一實物期權進行了預測，其意義在于不但增加了房地產交易的多樣性，對房地產行業的持續發展有所幫助，并且為購買力較弱的居民提供了更大的選擇空間．

[1] 薛 毅,陳立萍. R語言實用教程[M]. 北京:清華大學出版社, 2014.

XUE Yi, CHEN Liping.RLanguagePracticalTutorial[M]. Beijing: Tsinghua University Press, 2014. (in Chinese)

[2] 何曉群. 應用回歸分析[M]. 北京:中國人民大學出版社, 2014.

HE Xiaoqun.AppliedRegressionAnalysis[M]. Beijing: China Renmin University Press, 2014. (in Chinese)

[3] 王 妍. 房地產供需及房價的數學模型研究[D]. 杭州:浙江大學, 2012.

WANG Yan. Supply and demand of real estate and mathematical model study of real estate price [D]. Hangzhou:Zhejiang University, 2012. (in Chinese)

[4] 張德豐. MATLAB數值分析與應用[M]. 北京:國防工業出版社, 2007.

ZHANG Defeng.MATLABNumericalAnalysisandApplication[M]. Beijing: National Defense Industry Press, 2007. (in Chinese)

[5] AMRAM M, KULATILAKA N.RealOptions:ManagingStrategicInvestmentinanUncertainWorld[M]. Boston: Harvard Business School Press, 2001.

[6] SHREVE S E.StochasticCalculusforFinanceⅡ [M]. New York: Springer-Verlag New York Inc., 2004.

Nonlinearregressionmodelandoptionanalysisofrealestateprice

FENG Jinghai*, ZHU Junqiao

( School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China )

Based on macro-micro economics, a national average real estate price model is established by selecting several variables which may affect real estate price according to the data of National Bureau of Statistics website. By using R language, multiple linear regression analysis, multiple nonlinear regression analysis, correlation analysis, multicollinearity analysis, ridge regression analysis are used, and a number of linear and nonlinear models are obtained and compared with each other. Combined with the stochastic differential equation and real option, and some relevant knowledge of financial mathematics, the theoretical deduction, practical estimate of real estate model and pricing of real estate price option are carried out. A lot of simulations are carried out by using Matlab to get a good result.

real option; real estate price model; stochastic differential equation

1000-8608(2017)05-0545-06

2017-01-08；

2017-07-20．

國家自然科學基金資助項目(11371077，11571058)；中央高校基本科研業務費專項資金資助項目(DUT15LK19).

馮敬海*(1970-)，男，教授，碩士生導師，E-mail:physics_7@163.com；朱駿橋(1992-)，男，碩士，E-mail:zjqqq1018@126.com.

O211.9

A

10.7511/dllgxb201705016