Global exponential stability of cycle associative neural network with constant delays

SHI Renxiang

( School of Mathematical Sciences, Shanghai Jiao Tong University, Shanghai 200240, China )

Globalexponentialstabilityofcycleassociativeneuralnetworkwithconstantdelays

SHI Renxiang*

( School of Mathematical Sciences, Shanghai Jiao Tong University, Shanghai 200240, China )

The global exponential stability of cycle associative neural network with constant delays is discussed. During the discussion, by constructing homeomorphism mapping, it is demonstrated that there exists an equilibrium point which is unique for this system, then the global exponential stability of the unique equilibrium point is testified by constructing proper Lyapunov function. Similar to previous work about neural network stability, under the assumption that the activation function about neuron satisfies Lipschitz condition and the matrix constructed by correlation coefficient satisfies given condition, the dynamics of global exponential stability forn-layer neural network with constant delays are obtained. The results contain that when the passive rate of neuron is sufficiently large, the neural network is global exponential stable.

exponential stability; equilibrium point; neural network; Lyapunov function

0 Introduction

The dynamical behaviors of delayed neural networks have attracted increasing interest for their intense application. Especially, there are many works about stability of neural network[1-8]. In Lits. [2-3], the authors discussed the static network with S-type distributed delays. In Lit. [4], the author discussed the global exponential stability of a class of neural networks with delays by natureM-matrix. In Lits. [3-5], the authors discussed the global exponential stability of the one-layer neural network. At the same time, the stability of bidirectional associative memory neural networks of the two-layers with delays has also been studied by many researchers[6-8]. In Lits. [5-6] the authors discussed the existence of equilibrium point and the global exponential stability by homeomorphism and constructing proper Lyapunov function. Inspired by above work, we should discuss the exponential stability ofn-layers neural networks with constant delays, which should be taken as general form for work[6].

1 Model and preliminaries

In this paper, we should discuss the cycle associative neural network of then-layers with constant delays:

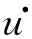
u.

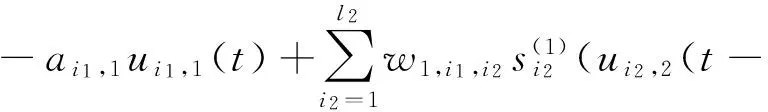
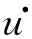
u.

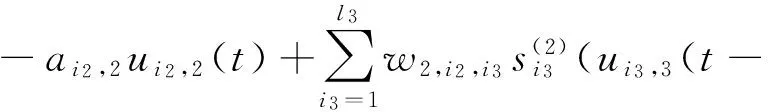
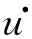
u.

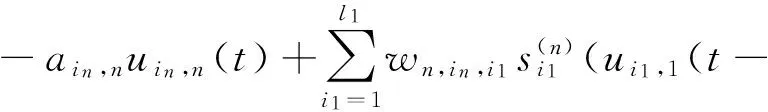
(1)

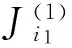
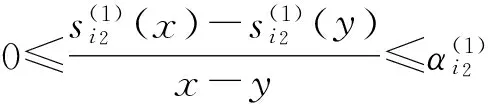
(2)

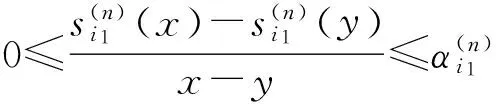
Letτ=max(τ1,τ2,…,τn), initial conditions for network (1) are of the form

φ=(φ1…φl1φl1+1…φl1+l2…φl1+l2+…+ln-1+1…φl1+l2+…+ln)∈C=C([-τ,0],Rl1+l2+…+ln)

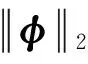
(u1(t,φ),u2(t,φ),…,un(t,φ))= (u1,1(t,φ) …ul1,1(t,φ)u1,2(t,φ) …ul2,2(t,φ) …u1,n(t,φ) …uln,n(t,φ))

Denotex=(u1u2…un)=(u1,1…ul1,1u1,2…ul2,2…u1,n…uln,n). Hence,we write network (1) as

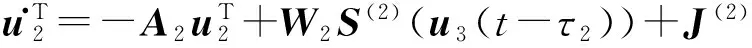
u.T2=-A2uT2+W2S(2)(u3(t-τ2))+J(2)

…

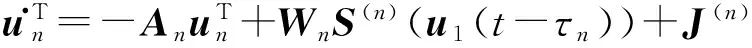
u.Tn=-AnuTn+WnS(n)(u1(t-τn))+J(n)

whereA1=diag{a1,1,…,al1,1},A2=diag{a1,2,…,al2,2}, …,An=diag{a1,n,…,aln,n}, andW1=(w1,i1,i2)l1×l2,W2=(w2,i2,i3)l2×l3, …,Wn=(wn,in,i1)ln×l1.

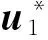
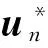
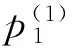
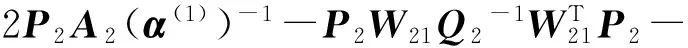
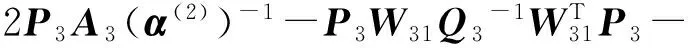
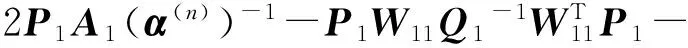
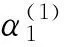
Theorem1For network (1), the assumption (2) and condition (T) hold. Then the neural network (1) has a unique equilibrium point.

Theorem2For network (1), the assumption (2) and condition (T) hold. Then the equilibrium point of neural network (1) is global exponential stable.

We should discuss the existence and uniqueness of the equilibrium point, the global exponential stability, and compare our result with previous results and give an example.

2 The existence and uniqueness of equilibrium point

For convenience we state the following lemma,which is special case of lemma (2.1) in Lit. [6].

Lemma1Given any real vectorsX,Yof appropriate dimensions, then the following inequality holds

…

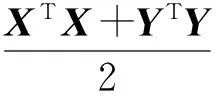
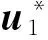
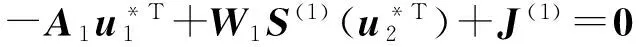
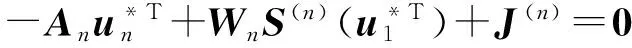
Let

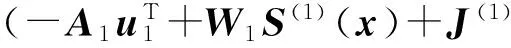
(3)

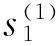
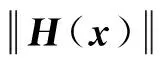
LetS(x)=(S(n)(x)S(1)(x) …S(n-1)(x))T,xandybe two vectors such thatx≠y. Under the assumption (2) on the activation functionsx≠yimply two cases: (i)x≠yandS(x)-S(y)≠0; (ii)x≠yandS(x)-S(y)=0, now we write

H1(x)-H1(y)=-A1u1x+A1u1y+W1(S(1)(x)-S(1)(y))

H2(x)-H2(y)=-A2u2x+A2u2y+W2(S(2)(x)-S(2)(y)) …

Hn(x)-Hn(y)=-Anunx+Anuny+Wn(S(n)(x)-S(n)(y))

(4)

whereu1x=(u1,1x…ul1,1x)T,u1y=(u1,1y…

ul1,1y)T,u2x=(u1,2x…ul2,2x)T,u2y=(u1,2y…

ul2,2y)T, …,unx=(u1,nx…uln,nx)T,uny=(u1,ny…uln,ny)T.

First, we consider the case (i). In this case,there existsk∈(1,2,…,n) such thatS(k)(x)≠S(k)(y). Multiplying both sides of the first equation in Eq. (4) by 2(S(n)(x)-S(n)(y))TP1, results in

2(S(n)(x)-S(n)(y))TP1(H1(x)-H1(y))= -2(S(n)(x)-S(n)(y))TP1(A1u1x-A1u1y)+ 2(S(n)(x)-S(n)(y))TP1W1(S(1)(x)-S(1)(y))

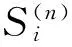
we have

(S(n)(x)-S(n)(y))TP1(A1u1x-A1u1y)≥ (S(n)(x)-S(n)(y))TP1A1(α(n))-1(S(n)(x)-S(n)(y))

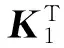
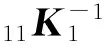
It follows from Lemma 1

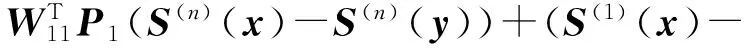
(5)

Similarly

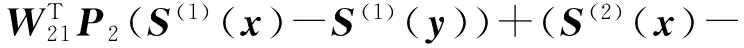
(6)

…

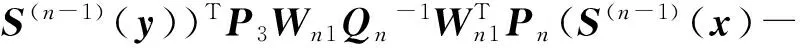
(7)

which imply that

Ψ(x,y)=(2(S(n)(x)-S(n)(y))T2(S(1)(x)-S(1)(y))T… 2(S(n-1)(x)-S(n-1)(y))T)diag{P1,P2,…,Pn}× (H(x)-H(y))

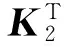
Ψ(x,y)≤-(S(1)(x)-S(1)(y))TΩ1(S(1)(x)-S(1)(y))-(S(2)(x)-S(2)(y))T×Ω2(S(2)(x)-S(2)(y))-…- (S(n)(x)-S(n)(y))TΩn(S(n)(x)-S(n)(y))<0

(8)

That isH(x)≠H(y). Sincediag{P1,P2,…,Pn} is a positive diagonal matrix,we prove thatH(x)-H(y)≠0whenx≠yandS(x)≠S(y).

Now we consider the case (ii). In view ofx≠yandS(x)-S(y)=0,we have

which implies thatH(x)≠H(y) forx≠y.

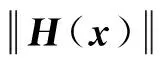
Ψ(x,0)≤-λmin[(S(x)-S(0))T(S(x)-S(0))]

whereλmindenotes the minimum eigenvalue of the positive definite matricesΩ1,Ω2, …,Ωn. Similar to Lemma 2.2 in Lit. [6], we obtain

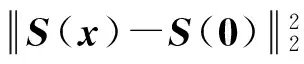
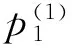
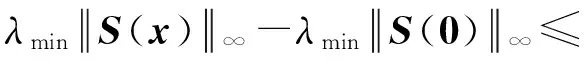
Hence

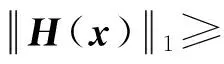
3 The global exponential stability of the equilibrium point

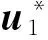
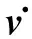
v.

1(t)=-A1v1(t)+W1f(1)(v2(t-τ1))

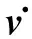
v.

2(t)=-A2v2(t)+W2f(2)(v3(t-τ2))

…

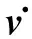
v.

n(t)=-Anvn(t)+Wnf(n)(v1(t-τn))

(9)

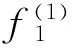
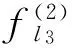
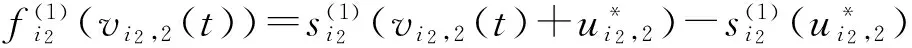
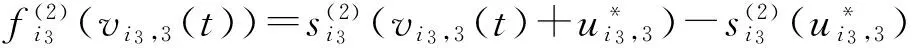
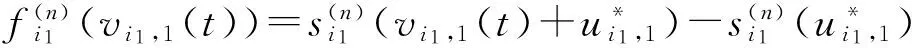
i1=1,2,…,l1

The Lipschitz condition implies that

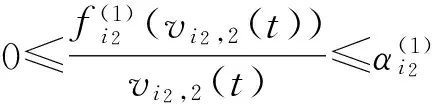
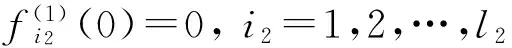
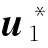
ProofofTheorem2We employ the following Lyapunov function

V(v1(t),v2(t),…,vn(t),t)=ε1V1(v1(t),v2(t),…,vn(t))+V2(v1(t),v2(t),…,vn(t),t)

(10)

where

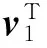
First we compute the derivative ofValong trajectories of Eq. (9), then determine positive constantε1and positive definite matricesR1,R2, …,Rn.

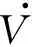
V.

(v1(t),v2(t),…,vn(t),t)=ε1

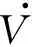
V.

1(v1(t),v2(t), …,vn(t))+

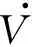
V.

2(v1(t),v2(t), …,vn(t),t)

where

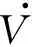
V.

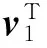
and

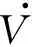
V.

2(v1(t),v2(t),…,vn(t),t)= 2f(1)T(v2(t))P2[-A2v2(t)+W2f(2)(v3(t-τ2))]+2f(2)T(v3(t))P3[-A3v3(t)+W3f(3)(v4(t-τ3))]+…+ 2f(n)T(v1(t))P1[-A1v1(t)+W1f(1)(v2(t-τ1))]+f(1)T(v2(t))R1f(1)(v2(t))-f(1)T(v2(t-τ1))×R1f(1)(v2(t-τ1))+f(2)T(v3(t))R2f(2)(v3(t))-f(2)T(v3(t-τ2))R2f(2)(v3(t-τ2))+…+f(n)T(v1(t))Rnf(n)(v1(t))-f(n)T(v1(t-τn))×Rnf(n)(v1(t-τn))

Rewriting

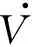
V.

1as

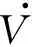
V.

It follows from Lemma 1 that

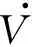
V.

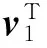
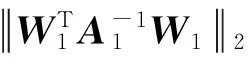
we get

-f(1)T(v2(t))P2A2v2(t)≤ -f(1)T(v2(t))P2A2(α(1))-1f(1)(v2(t)) -f(2)T(v3(t))P3A3v3(t)≤ -f(2)T(v3(t))P3A3(α(2))-1f(2)(v3(t)) … -f(n)T(v1(t))P1A1v1(t)≤ -f(n)T(v1(t))P1A1(α(n))-1f(n)(v1(t))

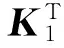
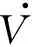
V.

2≤-f(1)T(v2(t))2P2A2(α(1))-1f(1)(v2(t))-f(2)T(v3(t))2P3A3(α(2))-1f(2)(v3(t))-…-f(n)T(v1(t))2P1A1(α(n))-1f(n)(v1(t))+ 2(f(1)T(v2(t))P2(W21K2-1)(K2W22)×f(2)(v3(t-τ2)))+2(f(2)T(v3(t))×P3(W31K3-1)(K3W32)f(3)(v4(t-τ3)))+…+ 2(f(n)T(v1(t))P1(W11K1-1)(K1W12)×f(1)(v2(t-τ1)))+f(1)T(v2(t))×R1f(1)(v2(t))-f(1)T(v2(t-τ1))×R1f(1)(v2(t-τ1))+f(2)T(v3(t))×R2f(2)(v3(t))-f(2)T(v3(t-τ2))×R2f(2)(v3(t-τ2))+…+f(n)T(v1(t))×Rnf(1)(v1(t))-f(n)T(v1(t-τn))×Rnf(n)(v1(t-τn))

That

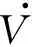
V.

2is bounded by Lemma 1.

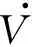
V.

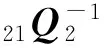
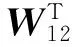
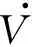
V.

2(v1(t),v2(t),…,vn(t),t)≤ -f(1)T(v2(t))(Ω1-2ε2Il2+ε2Il2)f(1)(v2(t))-f(2)T(v3(t))(Ω2-2ε2Il3+ε2Il3)f(2)(v3(t))-…-f(n)T(v1(t))(Ωn-2ε2Il1+ε2Il1)f(n)(v1(t))-ε2f(1)T(v2(t-τ1))f(1)(v2(t-τ1))-ε2f(2)T(v3(t-τ2))f(2)(v3(t-τ2))-…-ε2f(n)T(v1(t-τn))f(n)(v1(t-τn))≤ -ε2f(1)T(v2(t))f(1)(v2(t))-ε2f(2)T(v3(t))f(2)(v3(t))-…-ε2f(n)T(v1(t))f(n)(v1(t))-ε2f(1)T(v2(t-τ1))f(1)(v2(t-τ1))-ε2f(2)T(v3(t-τ2))f(2)(v3(t-τ2))-…-ε2f(n)T(v1(t-τn))f(n)(v1(t-τn))

Chooseε1>0 such thatMε1≤ε2, we have

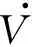
V.

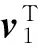
εε1+εpθ-ε1a+rθ2ετeετ<0

(11)

We obtain

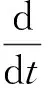
Noting that

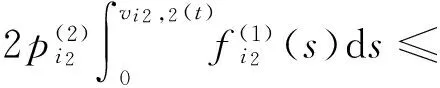
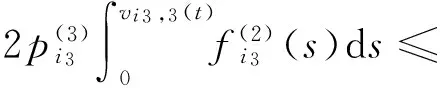
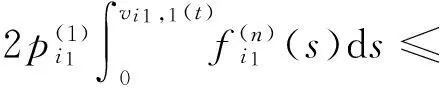
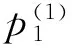
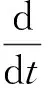
(12)

Integrating both sides of Eq. (12) from 0 tos, concerned with Eq. (11), similar to Theorem 2.3 in Lit. [6], we obtain

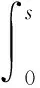
Therefore

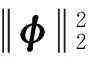
(13)

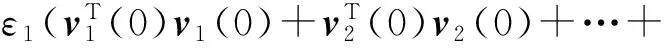
According to Eq. (13) and the above inequality

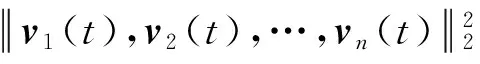
that is,

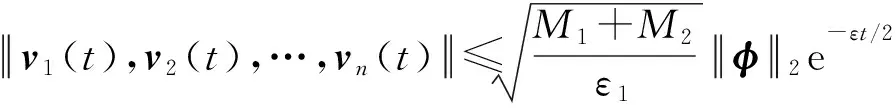
(14)

Inequality (14) implies that the origin of system (9) is global exponential stable.

4 Comparison with previous results

Now we compare our results with the previous result in Lit. [6], where authors gave a new sufficient condition for the existence, uniqueness and global stability of the equilibrium point for BAM neural network with constant delays:

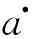
a.

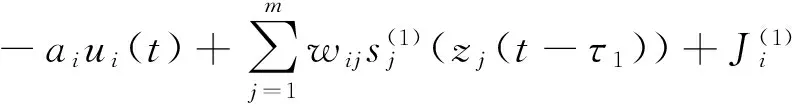
i=1,2,…,n

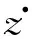
z.

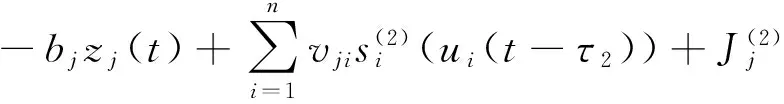
j=1,2,…,m

(15)

We could obtain the result in Lit. [6] from our work,whenn=2, network (1) is similar to Eq. (15), Theorems (1), (2) became Lemma (2.2), Theorem (2.3) in Lit. [6].

Example1Assume the parameters in Eq. (9) are given as follows:

andA1=A2=…=An=aIn,Q1=Q2=…=Qn=rIn, (α(1))-1=(α(2))-1=…=(α(n))-1=P1=P2=…=Pn=W11=W21=…=Wn1=In, whereInisn×nidentity matrix. Hence, we have

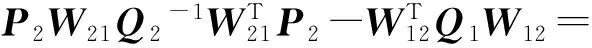
5 Conclusion

We study a class of neural networks with constant delays in this paper, comparing with previous work[6], we expand the result of neural network from 2-layer ton-layer by constructing Lyapunov function. Our result includes the result of work in Lit. [6].

[1] HAN Wei, LIU Yan, WANG Linshan. Robust exponential stability of Markovian jumping neural networks with mode-dependent delay [J].CommunicationsinNonlinearScienceandNumericalSimulation, 2010,15(9):2529-2535.

[2] WANG Yangfan, LU Chunge, JI Guangrong,etal. Global exponential stability of high-order Hopfield-type neural networks with S-type distributed time delays [J].CommunicationsinNonlinearScienceandNumericalSimulation, 2011,16:3319-3325.

[3] WANG M, WANG L. Global asymptotic robust stability of static neural network models with S-type distributed delays [J].MathematicalandComputerModelling, 2006,44:218-222.

[4] YANG Fengjian, ZHANG Chaolong, CHEN Chuanyong,etal. Global exponential stability of a class of neural networks with delays [J].ActaMathematicaeApplicataeSinica, 2009,25(1):43-50.[5] ZHAO Weirui, ZHANG Huanshui. Globally exponential stability of neural network with constant and variable delays [J].PhysicsLettersA, 2006,352(4/5):350-357.

[6] ZHAO Weirui, ZHANG Huanshui, KONG Shulan. An analysis of global exponential stability of bidirectional associative memory neural networks with constant time delays [J].Neurocomputing, 2007,70(7/9):1382-1389.

[7] DING Ke, HUANG Nanjing, XU Xing. Global robust exponential stability of interval BAM neural network with mixed delays under uncertainty [J].NeuralProcessingLetters, 2007,25(2):127-141.

[8] LI Chuandong, LIAO Xiaofang, ZHANG Rong. Delay-dependent exponential stability analysis of bi-directional associative memory neural networks with time delay: an LMI approach [J].Chaos,Solitions&Fractals, 2005,24(4):1119-1134.

[9] FORTI M, TESI A. New conditions for global stability of neural networks with application to linear and quadratic programming problems [J].IEEETransactionsonCircuitsandSystems-I:FundamentalTheoryandApplications, 1995,42(7):354-366.

1000-8608(2017)05-0537-08

帶有常時滯循環耦合神經網絡的全局指數穩定性

石 仁 祥*

( 上海交通大學 數學科學學院, 上海 200240 )

討論了帶有常時滯循環耦合神經網絡的全局指數穩定性，在討論過程中通過構造同胚映射論證了該系統平衡點的存在性與唯一性，再通過構造合適的Lyapunov函數論證唯一平衡點是全局指數穩定的．類似于已有的神經網絡穩定性方面工作，在神經元的激勵函數滿足Lipschitz條件且相關系數構成矩陣也滿足給定條件下，得到n層帶有常時滯的神經網絡全局指數穩定的動力學性質．所得結果同時也蘊含當神經元的衰減速率足夠大時，神經網絡是全局指數穩定的．

指數穩定性；平衡點；神經網絡；Lyapunov函數

O175.13；TP183

A

2016-10-07；

2017-06-20.

江蘇省自然科學基金資助項目(BK20131285).

石仁祥*(1983-)，男，博士生，E-mail:srxahu@aliyun.com.

SHI Renxiang*(1983-), Male, Doc., E-mail:srxahu@aliyun.com.

10.7511/dllgxb201705015

Receivedby2016-10-07；Revisedby2017-06-20.

SupportedbyNatural Science Foundation of Jiangsu (BK20131285).