三角形的性質在圓錐曲線中的應用

魏怡，王運行

甘肅省蘭州新區舟曲中學

三角形的性質在圓錐曲線中的應用

魏怡，王運行

甘肅省蘭州新區舟曲中學

圓錐曲線一直是高考的熱點，也是學生學習的難點，也是高中教學中的難點。圓錐曲線的難點就在于它可以與很多幾何圖形產生聯系，比如三角形，這也是高頻考點。如果學生能夠在學習中熟練運用這些技巧，一定會起到事半功倍的作用。

圓錐曲線；三角形

在全國二卷的選擇填空中，圓錐曲線經常出現在最后兩道題，以壓軸題的形式出現。在選擇題中對圓錐曲線進行考察時，對技巧這一部分考查的比較多，筆者就涉及圓錐曲線的選擇題進行了大量的比對，發現這一部分知識總是會與三角形的性質交融在一起進行考查。如果教師能夠在教學的過程中將這些技巧進行總結，將會提升學生在這類題目上的正確率。下面筆者總結了幾例三角形的性質與圓錐曲線交融的常考題型。

一、三角函數在圓錐曲線中的應用

-----→

例---1→：若以F為焦點的拋物線y2=4x上的兩點A，B滿足則弦AB的中點到準線的距離為？

分析：過A，B分別做準線l的垂線并與準線分別相交于A’，B’點，過B點作AA’的垂線，垂足為C。

假設BF=m,則AF=2m,利用拋物線的定義可知，BB’=C A‘=m,可得AC=m,BC=2 2m

總結：焦點弦問題是拋物線中的常考題型，如果能---夠--→利用---已→知條件構造三角形，將會簡化這類問題。該題中已知AF=2FB，利用準線構造直角三角形，∠BAC的正切就是焦點弦所在直線的斜率，避免了聯立方程組所-----產→生的---復→雜運算。因此，在拋物線中遇到焦點弦問題，并且已知AF=mFB，都可用上述幾何方法求得焦點弦所在直線的斜率。

例2：已知F1,F2為雙曲線點，點P為雙曲線C右支上一點，直線PF1與圓x2+y2=a2相切，且

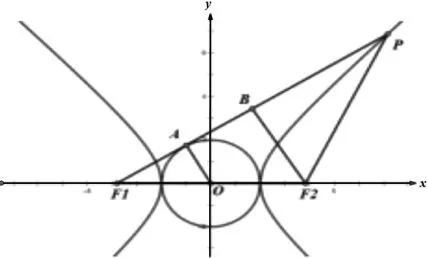
分析：如上圖所示，設直線PF1與圓的切點為點A，過F2做PF1的垂線，垂足為B，由題意可知，ΔOAF1與ΔF2BF1均為直角三角形。

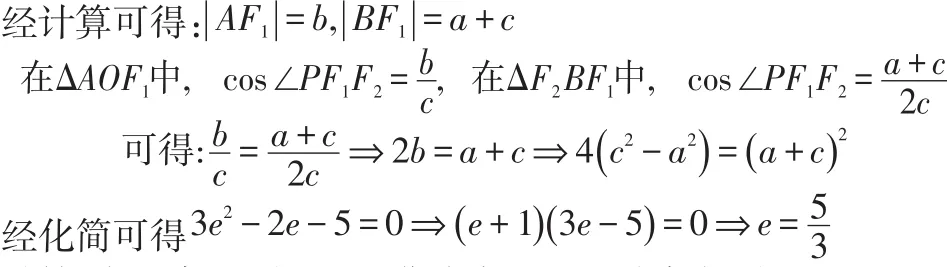
總結：離心率問題是圓錐曲線中的又一種常考題型，只要通過題目條件構造出有關a、b、c三者之間的關系式就可求得離心率。在該題中利用直角三角形的余弦公式作為橋梁，構造出等式，求出離心率，將復雜問題簡單化。

二、“兩邊之和大于第三邊，兩邊之差小于第三邊”在圓錐曲線中的應用

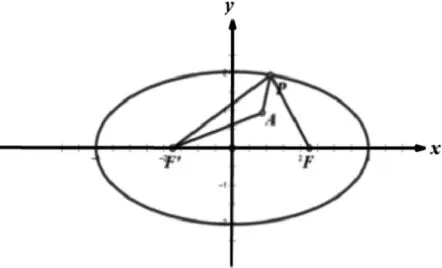
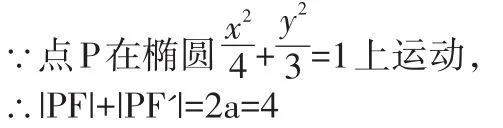
由此可得|PA|+|PF|=|PA|+（4-|PF'|）=4+（|PA|-|PF'|）

當P、A、F'三點共線，且P在AF'延長線上時，|PA|-|PF'|取得最大值。

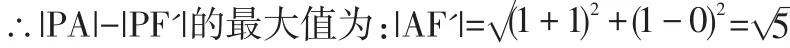
總結：此類問題屬于橢圓定義的常考題，考點是橢圓的第一定義和第二定義，無外乎這兩種考法，通過轉化的方式都可以將問題轉化為了一動點到一定點和到一定直線（定點）的距離最值問題，再利用三角形“兩邊之和大于第三邊，兩邊之差小于第三邊”的性質將問題解決。

三、“相似比”在圓錐曲線中的應用

例4：設拋物線y2=8x的焦點為F，不經過焦點的直線上有三個不同的點A，B，C,其中點A，B在拋物線上（點A在第一象限），點C在y軸負半軸上，則ΔBCF與ΔABF的面積之比是分析：設橢圓的左焦點為F'，連接PF'、AF'.

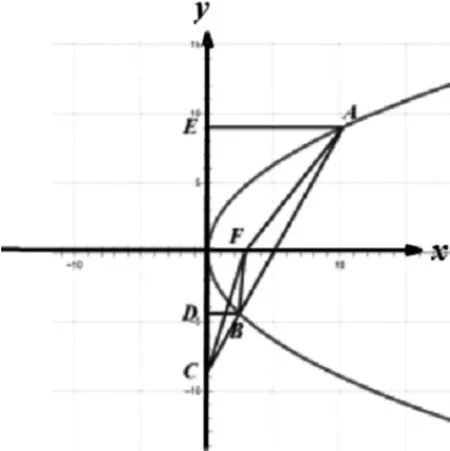
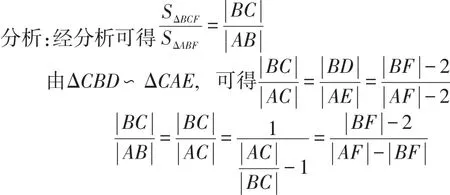
總結：該題中對拋物線的定義與三角形的相似原理進行了考查，利用相似比將問題轉化為定義問題，將復雜問題簡單化。

三角形是我們初中學習過的平面圖形，是我們較為熟悉的一部分知識，進入高中后我們又學習了正余弦定理，在初中的基礎上對三角形的性質進行了拓展。而圓錐曲線卻是學生學習的難點，但是學生如果能將三角形與圓錐曲線聯系起來，利用三角行的知識解決圓錐曲線的問題，能夠達到化繁為簡的效果，充分體現了高中數學中“復雜問題簡單化”的思想。當然在圓錐曲線的題目中，有很多的題目是非常復雜的，需要我們利用其它幾何圖形所具有的性質，這就需要教師引導學生勤于思考，善于發現。