基于斐波那契迭代算法的貝葉斯軟件可靠性驗證測試方案

馬振宇,， 吳 緯， 張 威， 劉福勝， 韓 坤

(1. 裝甲兵工程學院技術保障工程系， 北京 100072； 2. 裝甲兵工程學院信息工程系， 北京 100072；3. 北京特種車輛研究所， 北京 100072)

基于斐波那契迭代算法的貝葉斯軟件可靠性驗證測試方案

馬振宇1,2， 吳 緯3， 張 威2， 劉福勝1， 韓 坤3

(1. 裝甲兵工程學院技術保障工程系， 北京100072；2. 裝甲兵工程學院信息工程系， 北京100072；3. 北京特種車輛研究所， 北京100072)

針對軟件可靠性驗證測試方案不能真實反映軟件可靠性水平的問題，首先，根據貝葉斯原理構建了可靠性驗證測試方案框架，并給出超參數的求解辦法；然后，分析斐波那契排序規律，提出了斐波那契迭代算法；最后，提出了基于斐波那契迭代算法的貝葉斯軟件可靠性驗證測試方案，并對其進行實例驗證。結果表明：斐波那契迭代算法能夠真實地反映軟件實際失效概率；在相同的置信度條件下，基于斐波那契迭代算法的貝葉斯軟件可靠性驗證測試方案能夠明顯減少測試所需的測試用例數。

斐波那契迭代算法； 貝葉斯方法； 可靠性驗證測試； 軟件可靠性

軟件產品進行驗收時，為檢測軟件的可靠性指標是否達標，必須要通過軟件可靠性驗證測試[1]。通常情況下，驗證結果的置信度越高，軟件的可靠性越好，但會大幅增加測試人員的工作量。特別是針對一些技術復雜、成本高和可靠性高的軟件產品，驗收時所產生的經濟成本、人力成本和時間成本難以接受，導致軟件可靠性驗證測試難以進行。然而，使用貝葉斯方法(Bayesian method)可有效利用先驗信息，在保證高置信度的條件下，能夠顯著減少可靠性驗證測試的工作量。

目前，研究者針對貝葉斯軟件的可靠性驗證測試方法進行了大量工作。如：覃志東等[2-3]應用構造共軛分布的貝葉斯方法進行可靠性驗證，利用先驗信息為后驗提供大量的實驗信息，進而提出了基于先驗動態整合的可靠性驗證測試方法，該方法可很好地應用到實際工程中；王學成等[4]提出了基于減函數的先驗分布構造法進行測試驗證的方案，該方案在測試條件相同的情況下，可大幅縮短所需要的測試時長；劉廣等[5]提出了基于減函數的多層貝葉斯軟件可靠性驗證測試方法，該方案通過雙層貝葉斯方法進一步縮短了測試時長。

雖然前人[2-8]已進行了許多相關研究，但均在事先設定軟件可靠性指標的前提下開展軟件可靠性驗證測試工作，這使得測試結果難以真實客觀地反映軟件實際的可靠性。盡管已有的二分(折半)查詢法可解決該問題，但斐波那契迭代算法的查詢平均性能更優。因此，筆者通過斐波那契迭代算法，預期得到軟件的實際失效概率，并同時為軟件的驗證方法提供可靠性驗證測試方案。

1 基于貝葉斯方法的可靠性驗證測試方案

1.1基于貝葉斯方法的可靠性驗證測試方案框架

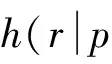
(1)

式中：p為被測軟件的可靠性參數。本文設定p為失效概率。

假設p的先驗分布函數為π(p)，則由失效概率和失效次數構成的聯合分布函數為

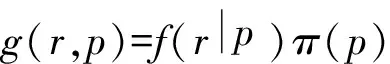
(2)

該函數將先驗信息和樣本信息有效地結合在一起。為了對p做出統計決策，引入條件分布(后驗分布)

(3)

將聯合分布函數進行變形，則有

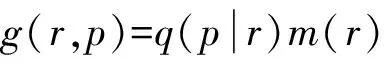
(4)

式中：

(5)

為邊緣分布函數。

設定軟件可靠性驗證測試方案的指標為(p0，c，rm)，其中p0為規定的軟件失效概率、c為置信度、rm為通過驗證測試時的最大失效次數，則驗證測試所需要的最小測試用例數nm為滿足下列不等式的最小整數解，即有

(6)

假設每次軟件測試均符合n重伯努利實驗[9-10]，那么在軟件可靠性驗證測試中，累計出現X次失效次數的概率符合二項分布，即

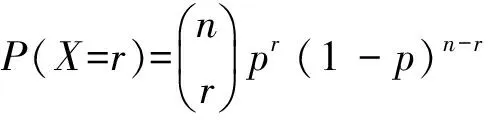
(7)

進一步推導出失效概率的先驗分布為貝塔分布，即

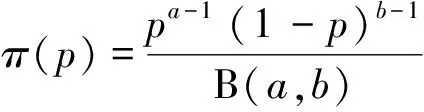
(8)

通常在結束軟件測試后，會得到n′個測試用例，其中共有r′次失效，則失效概率的后驗分布應為B(a+r′,b+n′-r′)，即

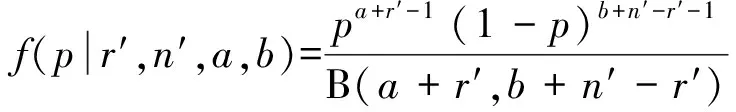
(9)

進行軟件可靠性驗證測試時，要求驗證結果不能出現失效。在無失效的情況下，最少測試用例數應為滿足下列不等式的最小整數解nm，即

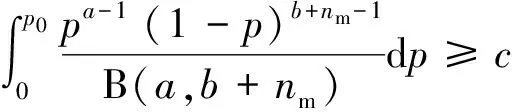
(10)

1.2超參數求解

根據超參數的求解原理[3]，可得超參數的具體估計過程為：首先，選用以往測試過程中遺留下的最后m組測試記錄作為先驗信息，每組含有l個測試用例；然后，統計每組測試用例中造成軟件失效的數量，分別記作k1,k2,…,km；最后，求得失效概率的經驗值tj=kj/l(j=1,2,…,m)。

結合式(5)、(7)、(8)，根據樣本的邊緣分布，可得

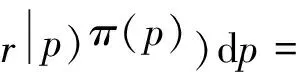
(11)

進而求得m(r)對應的一階矩為

(12)

同理，可得h(r)的二階矩，即

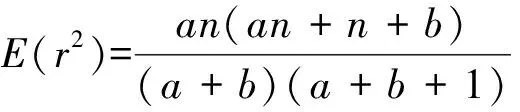
(13)

將E(r)、E(r2)記作w1、w2，則有

(14)

式中：D=(n-1)w12+n(w1-w2)。

w1、w2可通過經驗樣本值的期望估計得到，即

(15)

將式(15)代入式(14)中，即可估計出超參數a、b的值。

2 基于斐波那契迭代算法的貝葉斯驗證方案

2.1斐波那契迭代算法

斐波那契(Fibonacci)算法是依據對有序表進行斐波那契查找[11]演變而來，而斐波那契查詢法是在原有的二分(折半)查詢法基礎上改進而來，該方法在計算過程中只進行加減運算，不進行除法運算，因此斐波那契迭代算法查詢平均性能要比二分查詢法更優。

首先構造斐波那契序列，即

0,1,1,2,3,5,8,13,21,34,…。

(16)

由于任意一個有序序列的2個端點和中位點均與斐波那契數有聯系。根據斐波那契排列規律提出如下定義：

(17)

假設一個有序序列內共有m′個元素，且元素的個數等于某一個斐波那契數減去1，即m′=F(k)-1。若m′≠F(k)-1,則將該有序序列的最后1個元素重復填充到該序列，直到填充后序列中元素的個數與鄰近的斐波那契數減1相等為止。

斐波那契迭代算法的基本原理為：對于一個序列中元素個數為F(k)-1的有序序列，令中位點為Fmid=Fmin+F(k-1)-1，(其中Fmin為該有序序列中最小元素的值)，得到分割以后的序列，其中左子序列中元素的個數為F(k-1)-1，右子序列中元素的個數為(F(k)-1)-(F(k-1)-1)-1=F(k-2)-1。由此可以看出：2個子序列中元素的個數依舊滿足某一個斐波那契數減1，因此能夠反復對該序列進行分割。具體過程如下：

1)對相關變量進行初始化。Fmin=a′;Fmax=F(k),為該有序序列中最大元素的值，其中F=F(k)-1為該有序序列的長度;b′=F(k-1)-1，為中位點的相對偏移量。

2)若Fmin>Fmax，則查詢失敗；否則，Fmid=Fmin+b′。

3)若F(k)Fmid，則F=F-b′-1,b′=b′-F-1,Fmin=Fmid+1，繼續轉入步驟2)；若F(k)=Fmid，則表示查尋成功，結束該迭代過程。

2.2算法實現

一般來說，基于貝葉斯方法的軟件可靠性驗證測試均提前對其失效概率進行了假設，通常未考慮軟件本身實際的失效概率。為此，筆者在進行貝葉斯驗證之前，通過斐波那契算法來確定被測軟件的實際失效概率，這樣既可使用軟件實際的失效概率代替原來假設的失效概率，使軟件可靠性驗證測試過程更貼近實際；也可很好地利用先驗貝葉斯的優勢，在不降低試驗結果置信度的前提下，有效減少所需測試用例數。

首先，對軟件可靠性進行評估，可通過以往經驗估計出該軟件失效概率大致的取值范圍，并設定兩端的閾值；然后，通過斐波那契迭代算法找到實際失效概率的大致范圍(誤差不會超過1個數量級)；最后，確定軟件的實際失效概率。圖1為基于貝葉斯驗證的斐波那契迭代算法實現步驟，具體過程如下：

圖1 基于斐波那契迭代算法的貝葉斯驗證實現步驟

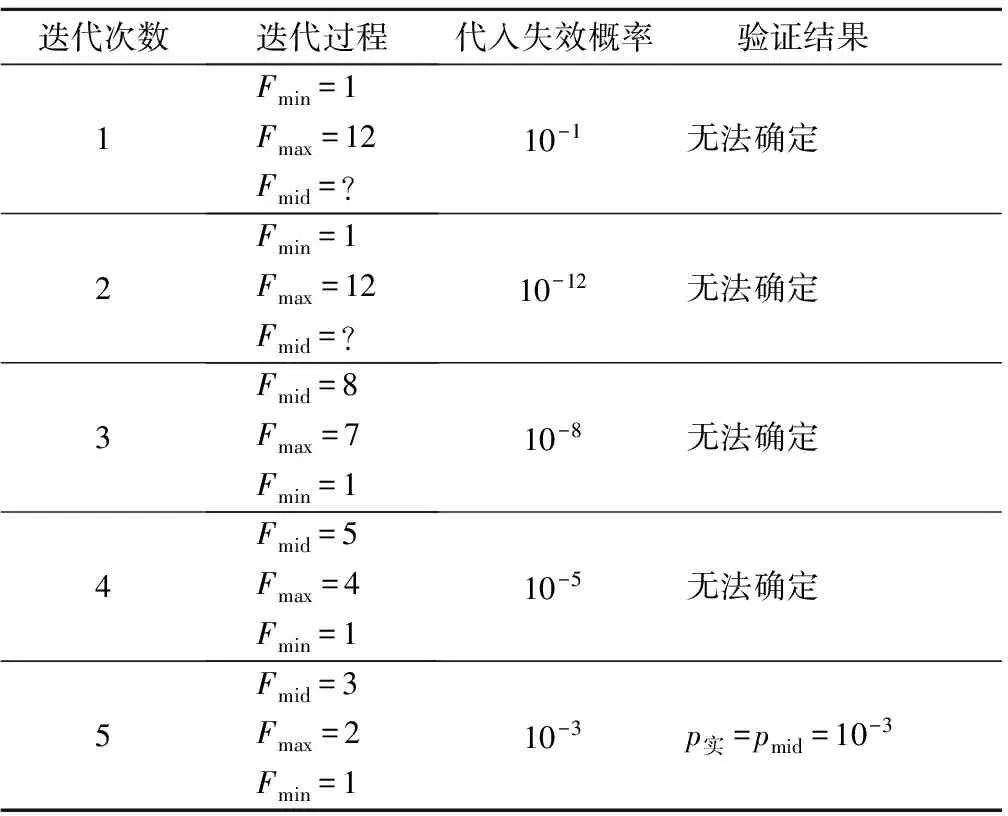
2)將(phigh,c)代入式(10)。若未出現失效，則p實

3)將(plow,c)代入式(10)。若未出現失效，則p實

4)令Fmid=Fmin+F(k-1)-1，將(pmid,c)代入式(10)。(1)若出現失效，則pmid≤p實

5)令Fmin=Fmin-1,phigh=10-Fmin，將(phigh,c)代入式(10)。若未出現失效，再將(0.1phigh-ε,c)、(0.1phigh+ε,c)分別代入式(10)，若結果分別是未失效、失效，則p實=0.1phigh，否則p實=phigh，此時迭代結束，求出最少測試用例數nm；若出現失效，則繼續重復執行步驟5)。

6)令Fmax=Fmax+1,plow= 10-Fmax,將(plow,c)代入式(10)。若出現失效，再將(plow-ε,c)、(plow+ε,c)分別代入式(10)，若結果分別是未失效、失效，則p實=plow，否則p實=10plow，此時迭代結束，求出最少測試用例數nm；若未出現失效，則繼續重復執行步驟6)。

3 實例驗證

試驗數據來自特種車輛軟件測評中心對某項目進行實測得到的數據結果。首先，根據斐波那契迭代算法求解出實測軟件的失效概率，假設Fmin=1,Fmax=12，構造一個差值為1的等差數列，那么phigh=10-1、plow=10-12，軟件自身的失效概率計算結果如表1所示；然后，收集軟件可靠性測試過程中最后10組數據作為先驗信息的歷史數據，每組測試用例數均為100000，每組出現的失效次數如表2所示；最后，依據本文提出的軟件可靠性驗證測試方案所得到的實驗結果，驗證該方法的有效性。

表1 基于斐波那契迭代算法的軟件自身失效概率計算結果

表2 先驗信息失效數據

由表1可知：在置信度為99%的條件下，實測軟件的失效概率為0.001。根據表2中的歷史信息，并結合式(12)-(15)，算出超參數a=1,b=2 067。

根據求得的軟件本身實際的失效概率值以及超參數的估計值，設定軟件可靠性驗證測試方案的可靠性指標(p0，c，rm)=(0.001，0.99，0)，即置信度為99%，失效概率為0.001，最大允許失效次數為0。結合式(10)可得：在有先驗信息的條件下，軟件可靠性測試所需測試用例數為2 536，在無先驗信息條件下所需測試用例數為4 602。這說明在保證置信度不變的條件下，所需測試用例數減少了2 066個，即可完成軟件可靠性驗證測試，論證了該方案的有效性。

4 結論

筆者基于斐波那契迭代算法求得被測軟件的自身實際失效概率，且客觀真實地反映出實測軟件的實際可靠性。另外，在保證相同的置信度條件下，基于斐波那契迭代算法的貝葉斯軟件可靠性驗證測試方案能夠顯著降低可靠性驗證測試所需測試用例數量。然而，對測試用例的選用如何做到完全隨機性選擇，還需要在以后的研究中進一步完善。

[1] 李海峰,劉暢,鄭軍.安全關鍵軟件可靠性驗證測試研究[J].航空標準化與質量,2013(3):46-50,58.

[2] 覃志東,雷航,桑楠,等.連續執行軟件可靠性驗證測試方法[J].計算機科學,2005,32(6):202-205.

[3] 覃志東,雷航,桑楠,等.安全關鍵軟件可靠性驗證測試方法研究[J].航空學報,2005,26(3):334-339.

[4] 王學成,陸民燕,李海峰,等.帶減函數的連續型軟件可靠性驗證方案[J].重慶大學學報(自然科學版),2012,35(10):136-143.

[5] 劉廣,黃百喬,劉暢,基于減函數的多層貝葉斯離散型軟件可靠性驗證測試方案[J].計算機應用研究,2017,33(3):761-764.

[6] 張文杰,楊華波,張士峰.基于Bayes混合驗前分布的成敗型產品可靠性評估[J].兵工學報,2016,37(3):505-511.

[7] 劉解放,劉思峰,方志耕.成敗型產品可靠性評價的加權Bayes方法[J].中國機械工程,2013,24(24):3371-3374.

[8] 馮文哲,劉琦.成敗型產品的Bayes可靠性驗證試驗設計[J].航空動力學報,2012,27(1):110-117.

[9] 劉海濤,張志華,董理.成敗型產品可靠性的Bayes驗收方案研究[J].兵工學報,2016,37(3):565-569.

[10] 劉琦,王囡,唐旻.成敗型產品基于驗后概率的Bayes序貫檢驗技術[J].航空動力學報,2013,28(3):494-500.

[11] 齊悅,夏克儉,姚琳.數據結構、算法與應用[M].北京：清華大學出版社,2015.

(責任編輯: 尚菲菲)

BayesianSoftwareReliabilityDemonstrationTestingSchemeBasedonFibonacciIterationAlgorithm

MA Zhen-Yu1,2, WU Wei3, ZHANG Wei2, LIU Fu-Sheng1, HAN Kun3

(1. Department of Technical Support Engineering, Academy of Armored Force Engineering, Beijing100072, China；2. Department of Information Engineering, Academy of Armored Force Engineering, Beijing100072, China;3. Beijing Special Vehicle Research Institute, Beijing100072, China)

The software reliability demonstration testing cannot really reflect the software reliability level. To solve that problem, the framework of software reliability demonstration testing is constructed according to the Bayesian principle, and the solution of parameters is also given. Then the Fibonacci sort principle is analyzed, and Fibonacci iteration algorithms proposed. Finally, a Bayesian software demonstration testing scheme based on Fibonacci iterative algorithms put forward and verified. Examples show that the Fibonacci iterative algorithm can reflect the actual software failure probability, Bayesian software demonstration testing scheme based on Fibonacci iterative algorithm can obviously reduce the number of testing cases at the same confidence level.

Fibonacci iteration algorithm; Bayesian method; reliability demonstration testing; software reliability

1672-1497(2017)04-0116-05

2017-05-04

軍隊科研計劃項目

馬振宇(1991-)，男，博士研究生。

O213.2；TP311.5

：ADOI：10.3969/j.issn.1672-1497.2017.04.022