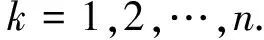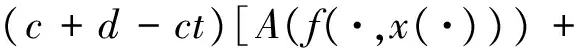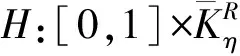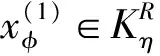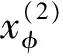脈沖微分方程m-點邊值問題的多重正解

李海艷, 王 敏, 李利玫

( 1. 四川大學(xué) 錦城學(xué)院, 四川 成都 611731; 2. 成都工業(yè)學(xué)院 人事處, 四川 成都 611730;3. 四川師范大學(xué) 數(shù)學(xué)與軟件科學(xué)學(xué)院, 四川 成都 610066)

脈沖微分方程m-點邊值問題的多重正解

李海艷1, 王 敏2, 李利玫3

( 1. 四川大學(xué) 錦城學(xué)院, 四川 成都 611731; 2. 成都工業(yè)學(xué)院 人事處, 四川 成都 611730;3. 四川師范大學(xué) 數(shù)學(xué)與軟件科學(xué)學(xué)院, 四川 成都 610066)

利用錐上的不動點指數(shù)定理研究一類脈沖微分方程的多點邊值問題,獲得了該問題多重正解的存在性新結(jié)果.

不動點指數(shù)定理; 脈沖微分方程;m-點邊值問題; 全連續(xù); 正解

帶有脈沖的微分方程邊值問題主要描述了一些現(xiàn)象在某一瞬時時刻的突變過程,在人口動態(tài)、物理學(xué)、生物學(xué)、工程學(xué)、神經(jīng)網(wǎng)絡(luò)等學(xué)科有著廣泛的應(yīng)用[1-3].微分方程作為一個重要的分支有著大量的研究成果[4-17],其中脈沖微分方程在數(shù)學(xué)方面有著更加豐富的內(nèi)容[11-17].

文獻(xiàn)[11]研究了多點邊值問題

其中,J=[0,1],f∈C(J×R+,R+),Ik∈C(R+,R+),0<ξ1<ξ2<…<ξm-2<1,ai,bi∈(0,+∞),i=1,2,…,m-2,應(yīng)用錐上的不動點定理獲得了多個正解的存在性定理.

考察二階脈沖微分方程的多點邊值問題(BVP)

(1)

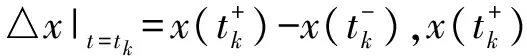
當(dāng)φ=1,a=c=1,b=d=0時,邊值問題將退化為文獻(xiàn)[11]研究的方程.本文利用錐上的不動點指數(shù)定理研究了一類脈沖微分方程的多點邊值問題,獲得了該問題多重正解的存在性新結(jié)果.

1 預(yù)備知識及主要引理

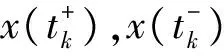
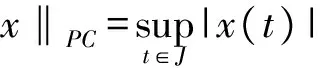
‖x‖=max{‖x‖PC,‖x′‖PC}.

顯然,PC[J,R]在‖·‖PC下構(gòu)成一個Banach空間,PC1[J,R]在‖·‖下構(gòu)成一個Banach空間.

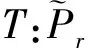
1) 如果x∈?Pr,有‖x‖≤‖Tx‖,則i(T,Pr,P)=0;

2) 如果x∈?Pr,有‖x‖≥‖Tx‖,則i(T,Pr,P)=1.

本文假設(shè)：

(H1)f∈C(J×R+,R+),Ik∈C(R+,R+);

(H2) △≠0,ρ=ac+ad+bc,其中

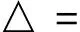
定義 1.1x稱為BVP(1)的一個解,若x∈PC[J,R+]∩C2(J′),x(t)>0,t∈J且x滿足(1)式.

引理 1.2 假設(shè)(H1)和(H2)成立,那么,x∈PC1[J,R+]∩C2(J′)是BVP(1)的解,當(dāng)且僅當(dāng)x是脈沖積分方程(2)的解.

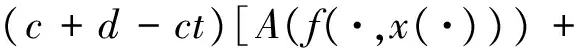
(2)

其中

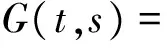
證明 為了方便證明,先驗證問題

(3)

的解滿足的脈沖積分方程.

設(shè)x∈PC1[J,R+]∩C2(J′)是BVP(3)的解,對(3)式積分可得

(4)

再次對(4)式兩端積分可得

(5)

在(4)和(5)式中分別令t=1有

(6)

(7)

由(6)和(7)式,再結(jié)合邊值條件可得

將x′(0)和x(0)代入(5)式有

則

因此有

(8)

(9)

所以,由(8)和(9)式有

令

即可得方程(3)的解滿足積分方程

故BVP(1)的解滿足積分方程

反過來,假定x是脈沖微分方程(2)的解,當(dāng)t≠tk時,對(2)式微分2次可得

易知

故x∈C2(J′),可以驗證

引理得證.

引理 1.3 假設(shè)(H1)成立,并且滿足

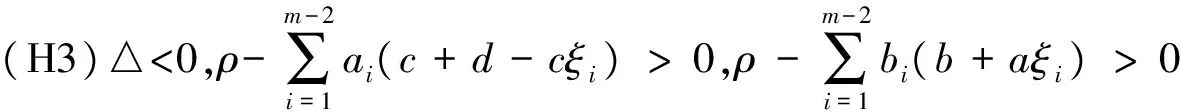
證明 由引理1.2,顯然G(t,s)≥0,且

故x(t)≥0,t∈J.

注 1.1 由G(t,s)的定義有

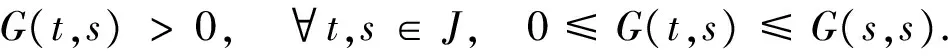
注 1.2 對?t∈Jθ,θ∈(0,1/2),Jθ=[θ,1-θ],s∈(0,1)有

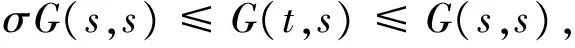
其中

且0<σ<1.

注 1.3 對?t,s∈Jθ,?ε>0,使得G(t,s)≥ε.

建立PC1[0,1]上的空間K,K={x∈PC1[0,1]:x≥0,t∈J}.

定義算子T:K→K如下

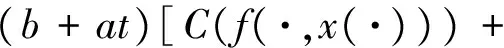
(10)

引理 1.4 假設(shè)(H1)和(H2)成立,則T(K)?K,且T:K→K是全連續(xù)算子.

證明 對x∈K,由算子T的定義及引理1.3,有Tx≥0,Tx∈PC1[0,1],且

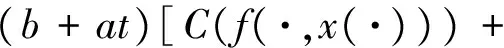
另一方面,由注1.2及0<σ<1有

所以,T(K)?K.此外由Ascoli-Arzela定理知T:K→K是全連續(xù)算子.

2 主要結(jié)論

為了方便,首先引入幾個記號:

定理 2.1 假設(shè)(H1)～(H3)成立.此外,f、Ik滿足下列條件：

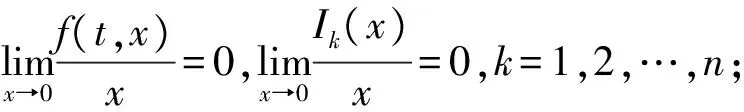
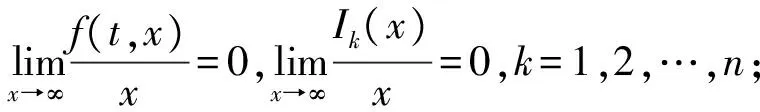
(H6) 存在正數(shù)η>0,使得對任意x≥η,t∈J,有f(t,x)>l,其中l(wèi)>0,

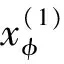
證明 令δ=εl(1-2θ)/η,k0=maxG(s,s),0

由(H4)可知,存在正數(shù)r滿足0

其中

因此,對任意x∈?Kr,由(10)式、注1.1和注1.2知

故對于任意x∈?Kr,得‖Tx‖<‖x‖,由引理1.1有

(11)

由(H5)知,存在m>0,使得對任意的x>m,t∈J有

令

則

取

從而對任意x∈?KR,由(10)式、注1.1和注1.2知

故對于任意x∈?KR,得‖Tx‖<‖x‖,由引理1.1有

(12)

另外,對任意

由上面的推導(dǎo)可知

(13)

另一方面,由(11)～(13)式并結(jié)合不動點指數(shù)的可加性

和

定理得證.

[1] NENOV S. Impulsive controllability and optimization problems in population dynamics[J]. Nonlinear Analysis:TMA,1999,36(7):881-890.

[2] KELLEY W G, PETERSON A C. Difference Equations:an Introduction with Applications[M]. New York:Academic Press,1991.

[3] ELAYDI S N. An Introduction to Difference Equations[M]. New York:Springer-Verlag,1996.

[4] 李萍,舒級,張佳,等. 一個具有相互作用非線性項的分?jǐn)?shù)階微分方程組的爆破解[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2016,39(1):15-19.

[5] 涂馨予,蒲志林. 一類帶一般記憶核的Cahn-Hilliard方程解的能量衰減估計[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2016,39(1):20-25.

[6] 魏君,蔣達(dá)清,祖力. 一維p-Laplace二階脈沖微分方程的奇異邊值問題[J]. 應(yīng)用數(shù)學(xué)學(xué)報,2013,36:414-430.

[7] 李耀紅,張曉燕. Banach 空間中一類二階非線性脈沖積分-微分方程邊值問題解的存在性[J]. 應(yīng)用數(shù)學(xué),2011,24(1):112-119.

[8] 尚亞亞,李永祥. 二階非線性積-微分方程邊值問題解的存在性[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2016,39(6):833-837.

[9] 廖家鋒,李紅英,段譽. 一類奇異p-Laplacian方程正解的唯一性[J]. 西南大學(xué)學(xué)報(自然科學(xué)版),2016,38(6):45-49.

[10] 郭麗君. 非線性微分方程三階三點邊值問題一個正解的存在性[J]. 四川師范大學(xué)學(xué)報(自然科學(xué)版),2016,39(6):846-850.

[11] FENG M Q, XIE D X. Multiple positive solutions of multi-point boundary value problem for second-order impulsive differential equations[J]. J Comput Appl Math,2009,223(1):438-448.

[12] 田景霞. 無窮區(qū)間上二階脈沖微分方程多點邊值問題的正解[J]. 應(yīng)用泛函分析學(xué)報,2012,4(3):315-320.

[13] SUN Y P. Positive solutions of nonlinear second-orderm-point boundary value problem[J]. Nonlinear Analysis,2005,61(7):1283-1294.

[14] TADEUSZ J. Positive solutions of three-point boundary value problems for second order impulsive differential equations with advanced arguments[J]. Appl Math Comput,2008,197(1):179-189.

[15] JIANG W H, GUO Y P. Multiple positive solutions for second-orderm-point boundary value problems[J]. J Math Anal Appl,2007,327(1):415-424.

[16] LIU X J, QIU J Q, GUO Y P. Three positive solutions for second-orderm-point boundary value problems[J]. Appl Math Comput,2004,156(3):733-742.

[17] JIANG W H. The existence of positive solutions for second-order multi-point BVPs with the first derivative[J]. Comput Math Appl,2009,225(2):387-392.

[18] GUO D J, LAKSHMIKANTHAM V. Nonlinear Problems in Abstract Cones[M]. New York:Academic Press Inc,1988.

[19] GUO D J, LAKSHMIKANTHAM V, LIU X Z. Nonlinear Integral Equations in Abstract Spaces[M]. Dordrecht:Kluwer Academic Publishers,1996.

2010 MSC：35Q55

(編輯 李德華)

Multiple Positive Solutions tom-point Boundary Value Problem for a Class of Impulsive Differential Equations

LI Haiyan1, WANG Min2, LI Limei3

( 1.JinchengCollege,SichuanUniversity,Chengdu611731,Sichuan; 2.DepartmentofPersonnel,CollegeofChengduTechnological,Chengdu611730,Sichuan; 3.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

Using the fixed point index theory, in this paper, we study them-point value problem for a class of impulsive differential equation. A new result for the existence of multiple positive solutions is given.

fixed point index theory; impulsive differential equation;m-point boundary value condition; completely continuous; positive solutions

2016-01-27

四川省教育廳自然科學(xué)青年基金(12ZB108)

李海艷(1983—),女,講師,主要從事非線性泛函分析的研究,E-mail:jclihaiyan2012@163.com

O175.8

A

1001-8395(2017)04-0457-07

10.3969/j.issn.1001-8395.2017.04.005