一類時滯SLARS網絡病毒傳播模型的周期解

趙 濤，魏蘇林，齊子健，張子振

（安徽財經大學 管理科學與工程學院，安徽 蚌埠 233030）

一類時滯SLARS網絡病毒傳播模型的周期解

趙 濤，魏蘇林，齊子健，張子振

（安徽財經大學 管理科學與工程學院，安徽 蚌埠 233030）

文章研究了一類具有分級感染率的時滯SLARS網絡病毒傳播模型。以模型的時滯為分岔參數，確定了產生Hopf分岔的時滯臨界點；利用中心流形定理和規范型理論確定了在時滯臨界點處產生的Hopf分岔的性質。

SLARS模型；時滯；Hopf分岔；周期解

0 引言

由于網絡病毒具有諸如破壞性、多態性以及不可預知性等典型特征，已經成為我們工作和日常生活最大的威脅之一[1-2]。對網絡病毒傳播過程進行動力學建模，是了解網絡病毒行為的一種有效方法。近年來，不少網絡病毒傳播模型被國內外學者相繼研究，并取得了一定的研究成果，如，SEIR模型[3-4]，SEIRS模型[5-6]，SEIQRS模型[7-8]等。但是以上具有潛伏狀態的網絡病毒傳播模型，大多都是假設潛伏狀態的主機不具備感染能力，并且考慮網絡病毒傳播過程中的時滯因素的也較少。最近，文獻[9]研究了如下潛伏狀態和活躍狀態主機均具有感染能力的時滯SLARS網絡病毒傳播模型：

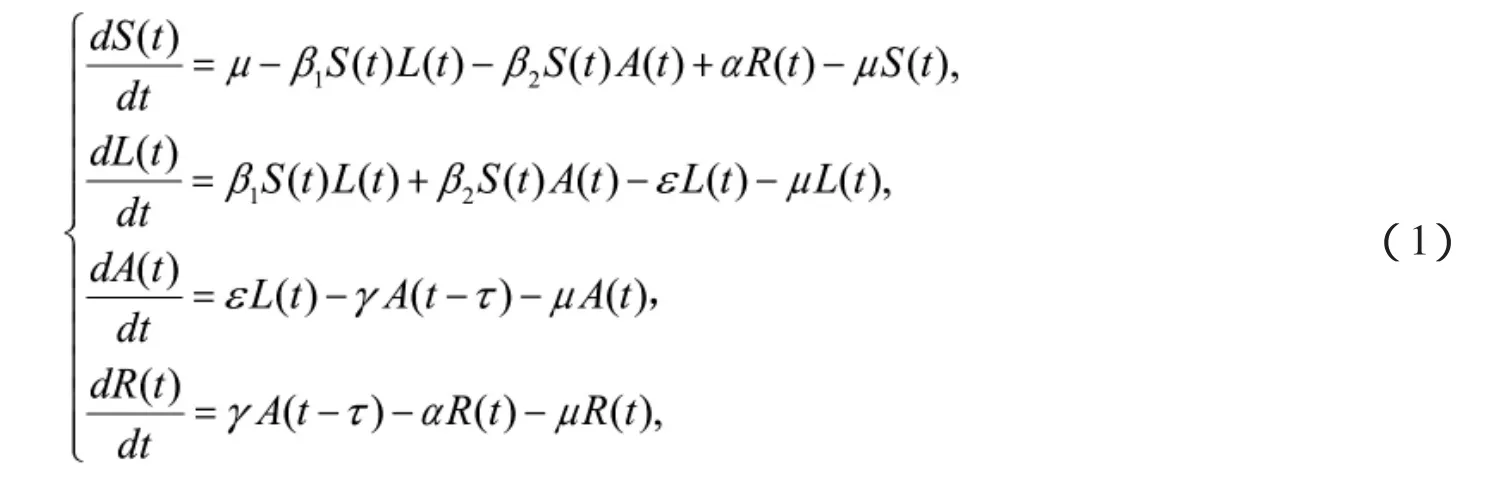
其中，S(t)，L(t)，A(t)和R(t)分別表示易感主機、處于潛伏狀態的主機、處于活躍狀態的主機以及處于恢復狀態的主機在t時刻所占的比例。μ為外部主機的聯網率和內部主機的斷網率；β1和β2分別為處于潛伏狀態的主機和處于活躍狀態的主機的感染率；α，ε和γ分別為狀態轉移率。為反病毒軟件查殺網絡病毒所需要的時間周期。

文獻[9]以反病毒軟件查殺網絡病毒所需要的時間周期所引起的時滯為分岔參數，研究了模型（1）的有病毒平衡點的局部漸近穩定性和局部Hopf分岔的存在性。對于一個動力系統模型而言，其動力學性質除了穩定性以外，還有持續性[10]，周期解[11]以及全局吸引性[12]等性質。本文在文獻[9]的基礎上，研究模型（1）的分岔周期解。

1 Hopf分岔的存在性

引理1[9]如果，則當∈[0，0)時，系統（1）局部漸近穩定。當=0時，系統（1）在 E(S*，L*，A*，R*)處產生 Hopf分岔，并且產生一簇分岔周期解。其中，

2 分岔周期解的穩定性

其中，

可以選取

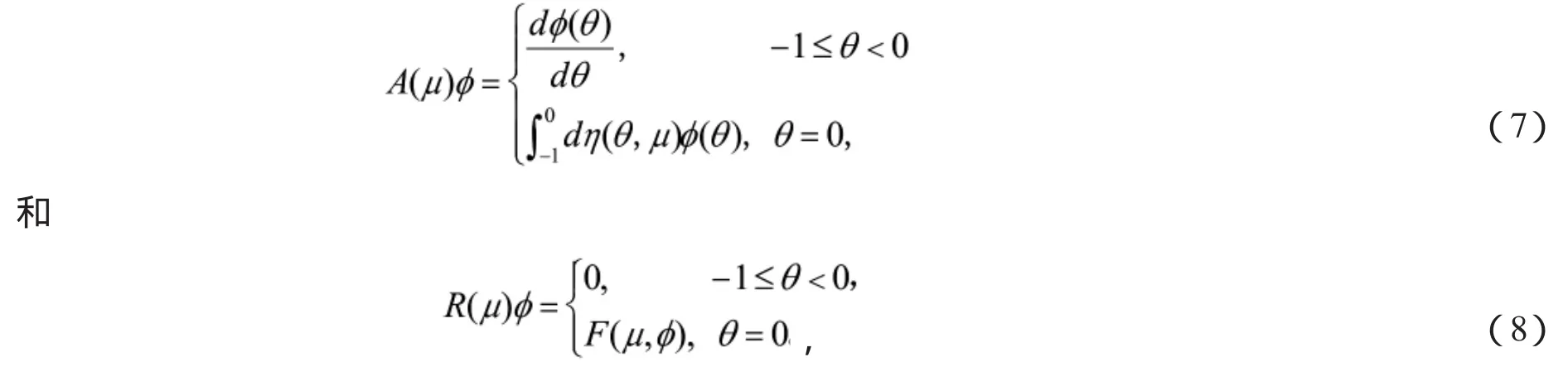
則系統（2）可以轉化為

以及雙線性內積

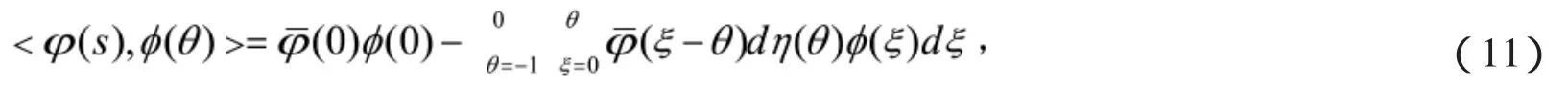
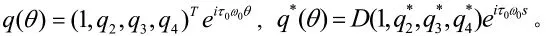
其中，

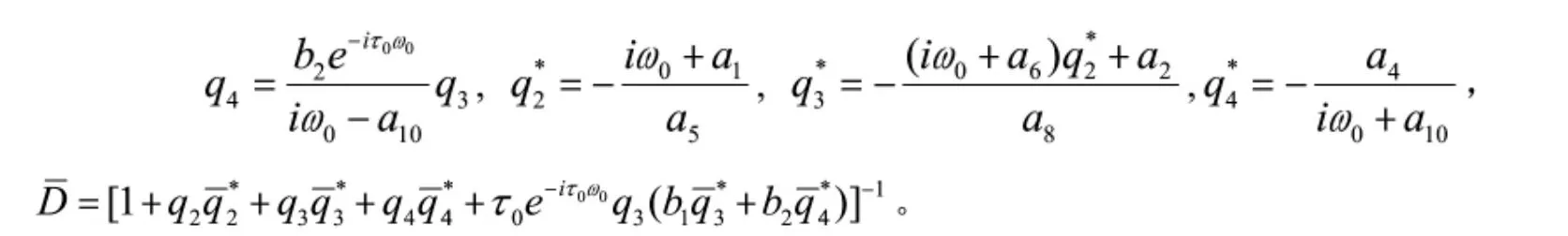
接下來，利用文獻[14]中的算法以及計算過程，可以得到下列參數表達式：

E1和E2可以根據下列方程得到

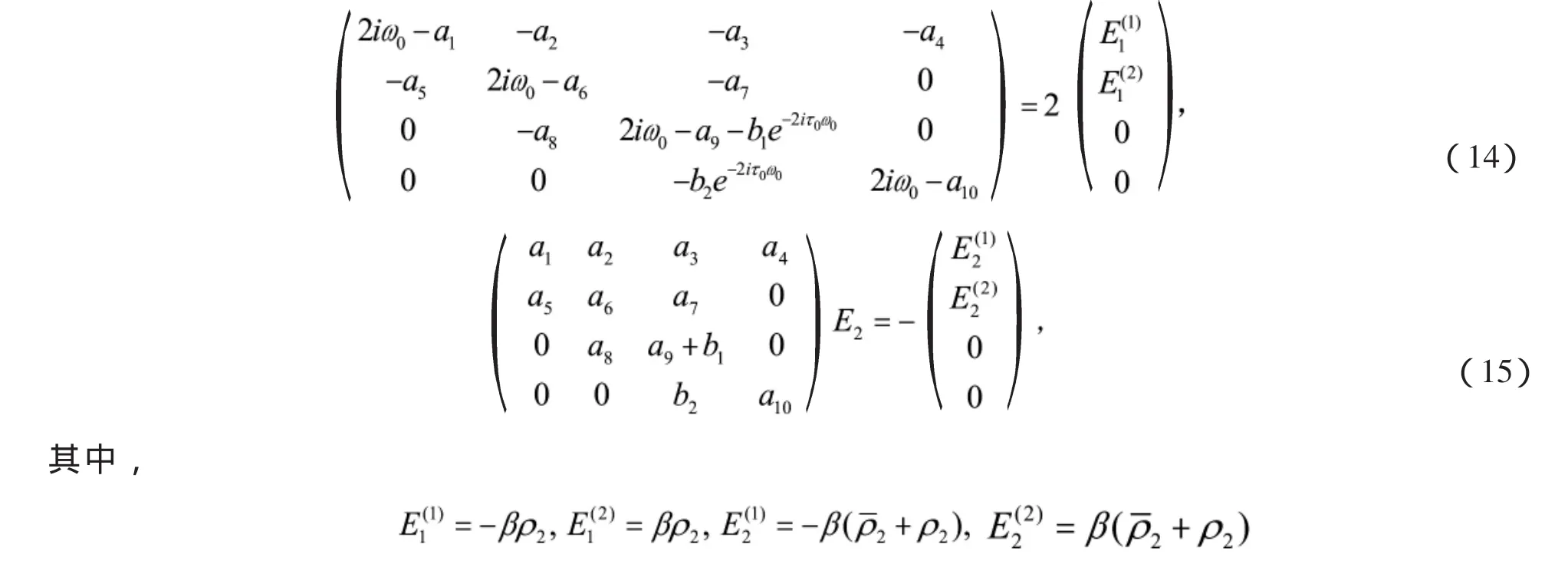
最后，可以計算得到下列參數的表達式：

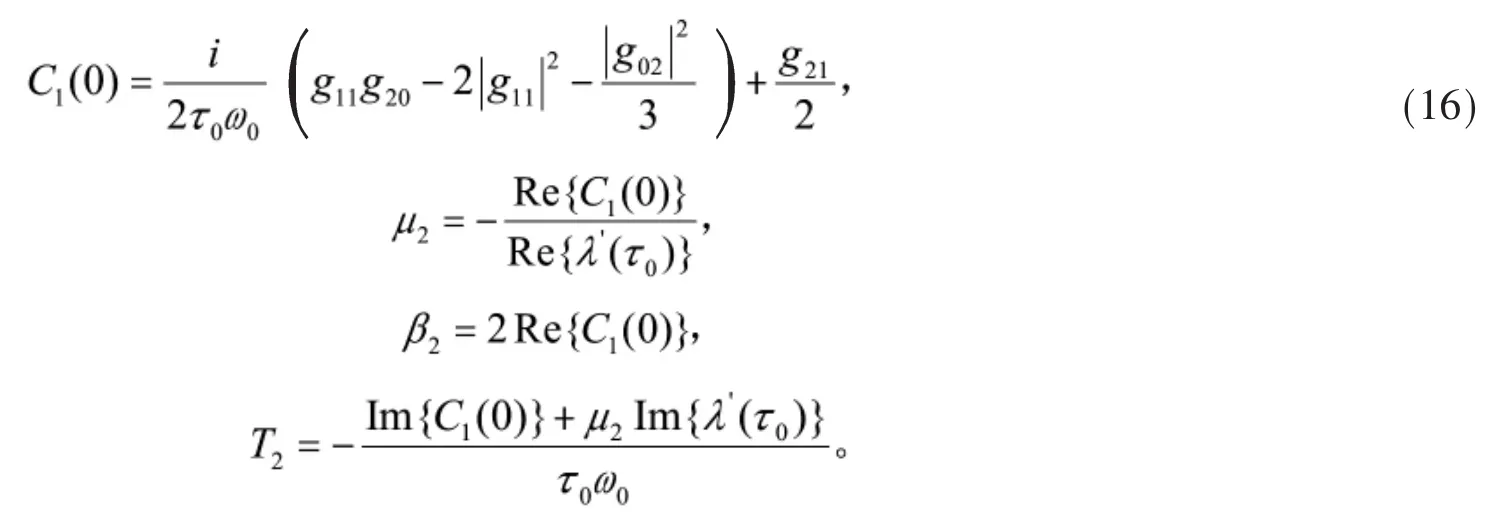
由上，可以得到如下關于分岔周期解的結論。

定理1 對于模型（1），當 μ2＞0(μ2＜0)，則 Hopf分岔是超臨界(次臨界)的；當 β2＜0(β2＞0)，則分岔周期解是穩定(不穩定)的；當 Τ2＞0(Τ2＜0)，則分岔周期解的周期是遞增(遞減)的。

3 仿真示例

直接計算得到，系統(17)的唯一有病毒平衡點 E(0.1116，0.2073，0.4936，0.1936)，進而得到。當時，如圖1所示，系統（17）是局部漸近穩定的。當時，系統（17）則失去穩定性，產生Hopf分支并在平衡點附近產生一簇分支周期解。仿真效果如圖2所示。另外，根據公式（16）計算得到，C1(0)=-21.6027+13.5870i，μ2=3.3172＞0，β2=-43.2054＜0，T2=-0.0427＜0。因此，根據定理1 可知，在附近產生的Hopf分岔是超臨界的，分岔周期解是穩定的并且其周期是遞增的。

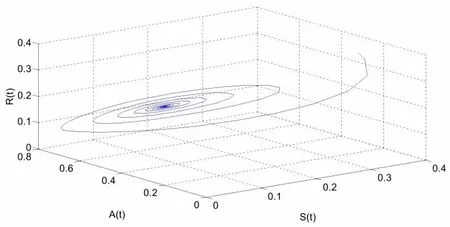
圖1 當時，系統（17）漸近穩定

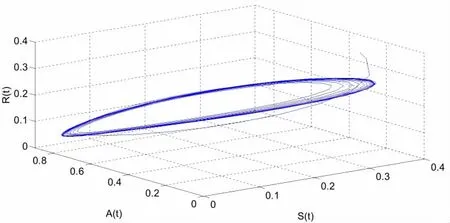
圖2 當時，系統（17）不穩定并發生Hopf分支

4 結論

本文在文獻[9]的基礎上，進一步研究了一類時滯SLARS網絡病毒傳播模型的分岔周期解，所得理論結果是對文獻[9]的適當補充。研究表明，當時滯t的取值足夠小時，模型處于理想的漸進穩定狀態，有利于網絡病毒傳播的控制。當時滯t的值越過臨界值時，模型將失去穩定，產生分岔周期解。此時，網絡病毒的傳播將失去控制。仿真結果表明，當滿足一定條件時，模型（1）中的四種狀態的主機數量將以周期震蕩形式共存。這種情況說明，模型中的時滯是有害時滯，應該盡量減小或者消除。在現實網絡中，可以通過不斷更新反病毒軟件以達到減小模型中的時滯，保證模型處于漸近穩定狀態。

[1]PIQUEIRA J R C，ARAUJO V O.A modified epidemiologicalmodel forcomputerviruses[J].Applied Mathematics and Computation，2009，213（2）：355-360.

[2]COHEN F.Computer virus：Theory and experiments[J].Computers&Security，1987，6（1）：22-35.

[3]彭梅，李傳東，何興.基于直接免疫的SEIR計算機病毒傳播模型[J].重慶師范大學學報，2013，30（1）：77-80.

[4]PENG M，HE X，HUANG J J，et al.Modeling computer virus and its dynamics[J].Mathematical Problems in Engineering，Article ID 842614，2013：1-5.

[5]MISHRA B K，SAINI D K.SEIRS epidemic model with delay for transmission of malicious objects in computer network[J].Applied Mathematics and Computation，2007，188（2）：1476-1482.

[6]WANG C L，CHAI S X.Hopf bifurcation of an SEIRS epidemic model with delays and vertical transmission in network[J].Advances in Difference Equations，2016，2016（1）：1-19.

[7]WANG F W，YANG F，ZHANG Y K.et al.Stability analysis of a SEIQRS model with graded infection rates for Internet worms[J].Journal of Computers，2014，9（10）：2420-2427.

[8]BADSHAH Q.Global stability of SEIQRS computer virus propagation model with non-linear incidence function[J].Applied Mathematics，2015，6（1）：1926-1938.

[9]張子振，尹發，緱超博.一類具有分級感染率的時滯網絡病毒傳播模型穩定性[J].蚌埠學院學報，2016，5（2）:19-22.

[10]野金花，朱煥.一類具有階段結構和Holling III類功能反應的捕食系統的一致持久性[J].黑龍江八一農墾大學學報，2017，29（1）：144-146.

[11]宋利民，張子振.具有隔離策略的網絡病毒傳播模型周期解[J].菏澤學院學報，2016，38（5）：56-62.

[13]劉昌東，江如，柴華金.一類具群體防御狀態及Holling III型功能反應的捕食系統正周期解的全局吸引性[J].廣東海洋大學學報，2016，36（3）：89-97.

[14]HASSARD B D，KAZARINOFF N D，WAN Y H.Theory and applications of hopf bifurcation[M].Cambridge University Press，Cambridg e，1981.

Periodic Solutions to a Delayed SLARS Computer Virus Propagation Model

ZHAO Tɑo，WEI Sulin，QI Zijiɑn，ZHANG Zizhen
（School of Management Science and Engineering，Anhui University of Finance and Economics，Bengbu Anhui 233030，China）

A series of delayed SLARS computer virus propagation model with graded infection rate was studied in this paper.Taking the delay of the model as bifurcation parameter，the critical point of time delay for Hopf bifurcation has been determined.Meanwhile，based on the central manifold theorem and the canonical form theory，the properties of the Hopf bifurcation at the critical point of the delay has been determined in this paper.

SLARS Model；Delay；Hopf Bifurcation；Periodic Solution

O175.12

A

1009-8666（2017）08-0025-06

［責任編輯、校對：李書華］

10.16069/j.cnki.51-1610/g4.2017.08.006

2017-04-02

2014年度安徽省高等學校自然科學項目“基于網絡斷層掃描的Ad Hoc網絡測量技術研究”（KJ2014A006）；2016年度安徽省自然科學研究項目“基于網絡層析成像的Ad Hoc網絡測量模型與方法研究”（1608085QF145）

趙濤（1981—），男，安徽蚌埠人。安徽財經大學副教授，博士，研究方向：網絡安全；魏蘇林（1971—），男，安徽蚌埠人。安徽財經大學講師，碩士，研究方向：網絡安全。