基于自適應(yīng)動態(tài)面及控制分配的敏捷導(dǎo)彈自動駕駛儀設(shè)計

任高峰， 胥 彪， 張金鵬,3

(1.中國空空導(dǎo)彈研究院， 河南 洛陽 471009； 2. 南京航空航天大學(xué) 航天學(xué)院， 南京 210016； 3.航空制導(dǎo)武器航空科技重點(diǎn)實(shí)驗(yàn)室， 河南 洛陽 471009)

基于自適應(yīng)動態(tài)面及控制分配的敏捷導(dǎo)彈自動駕駛儀設(shè)計

任高峰1， 胥 彪2， 張金鵬1,3

(1.中國空空導(dǎo)彈研究院， 河南 洛陽 471009； 2. 南京航空航天大學(xué) 航天學(xué)院， 南京 210016； 3.航空制導(dǎo)武器航空科技重點(diǎn)實(shí)驗(yàn)室， 河南 洛陽 471009)

根據(jù)自適應(yīng)動態(tài)面控制理論和動態(tài)控制分配算法， 提出了一種直接側(cè)向力與氣動力復(fù)合控制的敏捷型導(dǎo)彈自動駕駛儀設(shè)計方法。 敏捷型導(dǎo)彈擁有側(cè)噴發(fā)動機(jī)和舵機(jī)兩套控制執(zhí)行機(jī)構(gòu)， 為了提高兩套執(zhí)行機(jī)構(gòu)共同作用的控制效果， 導(dǎo)彈控制系統(tǒng)設(shè)計分為虛擬控制律設(shè)計和控制分配算法設(shè)計。 考慮系統(tǒng)模型的不確定性和外界干擾的影響， 結(jié)合動態(tài)面控制和自適應(yīng)控制的思想設(shè)計了虛擬控制律， 然后通過控制分配算法將虛擬控制律產(chǎn)生的控制量分配給實(shí)際執(zhí)行機(jī)構(gòu)。 仿真結(jié)果表明， 該方法設(shè)計的自動駕駛儀對過載的響應(yīng)快速且平穩(wěn)。 跟蹤過程中， 側(cè)噴發(fā)動機(jī)和舵機(jī)相互配合， 發(fā)揮了兩套執(zhí)行機(jī)構(gòu)共同作用的效果。

導(dǎo)彈； 自動駕駛儀； 動態(tài)面控制； 自適應(yīng)控制； 控制分配

0 引 言

現(xiàn)代無人戰(zhàn)斗機(jī)、 高超聲速飛行器、 彈道導(dǎo)彈性能的提高， 使得傳統(tǒng)純氣動控制的攔截彈難以精確命中來襲目標(biāo)。 先進(jìn)攔截彈一般采用多套執(zhí)行機(jī)構(gòu)來增強(qiáng)機(jī)動能力， 確保對目標(biāo)的直接碰撞殺傷。 這些執(zhí)行機(jī)構(gòu)通常有氣動舵和側(cè)噴發(fā)動機(jī)。 與氣動舵控制相比， 直接側(cè)向力能夠通過側(cè)噴發(fā)動機(jī)點(diǎn)火產(chǎn)生的反作用力來改變導(dǎo)彈的姿態(tài)， 提高導(dǎo)彈的過載響應(yīng)速度[1-3]。

滑模控制方法對模型不確定性和外界干擾具有較強(qiáng)的魯棒性， 較早地應(yīng)用于直接側(cè)向力與氣動力復(fù)合控制的導(dǎo)彈控制系統(tǒng)設(shè)計[4]。 文獻(xiàn)[5]基于狀態(tài)觀測器， 設(shè)計了復(fù)合控制導(dǎo)彈自適應(yīng)滑模控制律。 針對安裝有姿軌混合側(cè)向推力裝置的導(dǎo)彈， 文獻(xiàn)[6]采用動態(tài)滑動流形理論研究了導(dǎo)彈自動駕駛儀的設(shè)計問題。

文獻(xiàn)[7]針對導(dǎo)彈三維非線性模型采用θ-D方法設(shè)計了非線性控制律。 這種方法實(shí)際上可以看作是狀態(tài)依賴Riccati方法的一個變種形式。 文獻(xiàn)[8]基于有限時間理論和反步法提出了一種復(fù)合控制導(dǎo)彈自動駕駛儀的設(shè)計方法。 但是反步法在系統(tǒng)階次比較高時導(dǎo)數(shù)項(xiàng)計算量比較大， 反而使設(shè)計變得復(fù)雜。 對于大氣層內(nèi)攔截彈， 文獻(xiàn)[9]提出了一種基于反饋線性化的控制系統(tǒng)設(shè)計方法。 文獻(xiàn)[10]考慮了導(dǎo)彈執(zhí)行機(jī)構(gòu)飽和問題， 采用凸優(yōu)化的思想提出了一種導(dǎo)彈飽和非線性控制系統(tǒng)設(shè)計方法。 但是以上幾種方法都沒有充分考慮直接側(cè)向力和氣動力的相互配合問題。

控制分配算法是處理擁有冗余執(zhí)行機(jī)構(gòu)控制系統(tǒng)設(shè)計的一種有效方法[11-14]。 文獻(xiàn)[15]基于執(zhí)行機(jī)構(gòu)力控制和力矩控制結(jié)合控制分配算法， 分別研究了復(fù)合控制導(dǎo)彈控制系統(tǒng)設(shè)計時執(zhí)行機(jī)構(gòu)的相互配合問題。 文獻(xiàn)[16]采用反步法和L2最優(yōu)控制分配策略， 提出了一種自動駕駛儀設(shè)計方法。 但這些文獻(xiàn)都沒有考慮導(dǎo)彈脈沖發(fā)動機(jī)點(diǎn)火取整誤差帶來的影響。

本文考慮了模型不確定性和外界干擾的影響， 結(jié)合Lyapunov穩(wěn)定理論設(shè)計了參數(shù)自適應(yīng)律， 在此基礎(chǔ)上提出了一種直接側(cè)向力與氣動力復(fù)合控制導(dǎo)彈自動駕駛儀設(shè)計方法。 設(shè)計過程分為兩步: 首先采用動態(tài)面控制方法[17]， 設(shè)計虛擬控制律； 然后將虛擬控制律產(chǎn)生的控制量通過動態(tài)控制分配算法分配給實(shí)際執(zhí)行機(jī)構(gòu)。

1 敏捷導(dǎo)彈的數(shù)學(xué)模型

軸對稱導(dǎo)彈俯仰方向運(yùn)動方程為

(1)

式中：α為攻角；ωz為俯仰角速率；δz為升降舵偏角；fy為側(cè)噴發(fā)動機(jī)產(chǎn)生的直接側(cè)向力；q為來流動氣壓；Sm為特征參考面積；Lm為導(dǎo)彈特征長度；m為導(dǎo)彈質(zhì)量；Vm為導(dǎo)彈飛行速度；lm為導(dǎo)彈質(zhì)心到側(cè)噴發(fā)動機(jī)的距離；Jz為俯仰轉(zhuǎn)動慣量；cα，cδ和mα，mω，mδ分別為氣動力系數(shù)和氣動力矩系數(shù)。

導(dǎo)彈主要依靠力矩改變姿態(tài)建立攻角， 舵偏角和直接側(cè)向力引起的攻角變化量很小， 將其視為干擾。 定義x1=α，x2=ωz， 系統(tǒng)的狀態(tài)方程可以寫為

(2)

(3)

其中，

(4)

(5)

模型不確定性誤差、 氣動參數(shù)誤差以及外界干擾都可以歸入到參數(shù)w1和w2中。 假設(shè)干擾項(xiàng)d1和d2是有界的， 且滿足

(6)

式中:d1和d2為未知常數(shù)。 導(dǎo)彈的法向過載為

(7)

上述控制系統(tǒng)共有2個控制輸入， 分別為δz和fy， 每個控制量都可以單獨(dú)控制導(dǎo)彈姿態(tài)。 顯然， 控制輸入是冗余的。 將這兩個控制量視為一個整體， 定義一個虛擬控制量v：

v=Gu

(8)

這樣， 兩個控制量就變成一個虛擬控制量。 控制系統(tǒng)設(shè)計的問題就轉(zhuǎn)換為虛擬控制律的設(shè)計和控制分配算法的設(shè)計問題。

2 自適應(yīng)動態(tài)面控制律設(shè)計

2.1 控制律設(shè)計

定義動態(tài)誤差面S1和S2:

S1=x1-x1d，S2=x2-x2d

(9)

其中，x1d和x2d分別表示x1和x2的期望值， 且x1d滿足

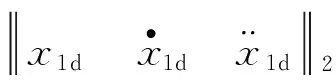
(10)

其中，κ為常數(shù)。 導(dǎo)彈的控制系統(tǒng)看作級聯(lián)的兩個部分， 首先設(shè)計虛擬控制量x2d， 將式(2)中x2看作子系統(tǒng)的輸入， 第一個誤差面的導(dǎo)數(shù)為

(11)

選擇Lyapunov函數(shù)：

(12)

其沿系統(tǒng)狀態(tài)軌跡的導(dǎo)數(shù)為

(13)

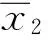
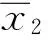
(14)

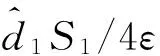
(15)

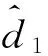
(16)

式中：μ1>0， 為自適應(yīng)增益；σ1>0， 常值。

(17)

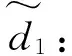
(18)

(19)

考慮如下增廣Lyapunov函數(shù)：

(20)

其沿系統(tǒng)狀態(tài)軌跡的導(dǎo)數(shù)為

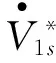
(21)

式中:

(22)

將式(16)代入式(22)整理后可得

(23)

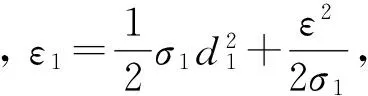
(24)

式(24)中右邊第一項(xiàng)和第二項(xiàng)為負(fù)， 第三項(xiàng)將在穩(wěn)定性分析中考慮。 接下來完成虛擬控制量v的設(shè)計， 考慮第二個動態(tài)面S2， 對其求導(dǎo)可得

(25)

選擇Lyapunov函數(shù)：

(26)

其沿著系統(tǒng)狀態(tài)軌跡的導(dǎo)數(shù)為

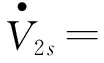
(27)

與上面設(shè)計x2d的思想類似， 虛擬控制量v設(shè)計為

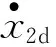
(28)

式中, 自適應(yīng)項(xiàng)滿足:

(29)

其中， 自適應(yīng)增益μ2>0； 參數(shù)σ2>0。 定義估計誤差項(xiàng)：

(30)

考慮增廣Lyapunov函數(shù)：

(31)

沿系統(tǒng)狀態(tài)軌跡對其求導(dǎo)可得

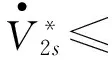
(32)

其中，φ2的表達(dá)式為

(33)

將式(29)代入式(33)可得

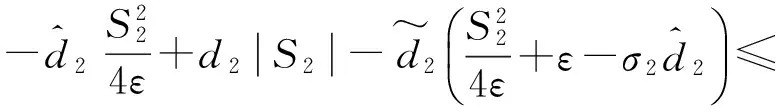
(34)

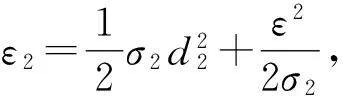
(35)

2.2 穩(wěn)定性分析

根據(jù)前面設(shè)計的自適應(yīng)動態(tài)面控制律， 導(dǎo)彈閉環(huán)控制系統(tǒng)可以表示為

(36)

(37)

(38)

(39)

(40)

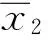
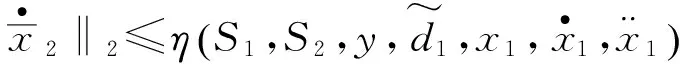
(41)

選取Lyapunov函數(shù)：

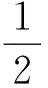
(42)

根據(jù)式(38)， 對其求導(dǎo)可得

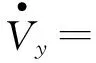
(43)

整個閉環(huán)系統(tǒng)的Lyapunov函數(shù)選取為

(44)

首先考慮集合

顯然Ω1是緊集。 再考慮集合

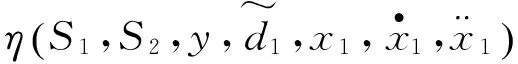
(45)

其中，c1>0,c2>0, 均為常數(shù)。 低通濾波器時間常數(shù)選取為

(46)

其中，c3>0為常數(shù)。 沿系統(tǒng)狀態(tài)軌跡對Lyapunov函數(shù)式(44)求導(dǎo)：

(47)

將式(24)、 式(35)、 式(43)、 式(45)～(46)代入式(47)可得

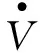
(48)

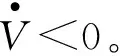
3 動態(tài)控制分配算法

上述過程求得的虛擬控制律v并不是每個執(zhí)行機(jī)構(gòu)真實(shí)的控制量。 通過動態(tài)控制分配算法[11-12]將虛擬控制量分配給執(zhí)行機(jī)構(gòu)， 使執(zhí)行機(jī)構(gòu)之間互相配合， 可以更好地發(fā)揮執(zhí)行機(jī)構(gòu)的效能。 控制輸入滿足約束條件：

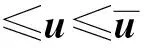
(49)

其中，

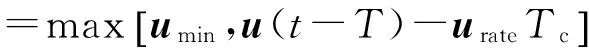
(50)

(51)

式中:umin和umax分別表示執(zhí)行機(jī)構(gòu)幅值限制的下界和上界；urate表示執(zhí)行機(jī)構(gòu)最大速率限制；Tc表示控制分配采樣時間。 設(shè)動態(tài)控制分配的表達(dá)式為

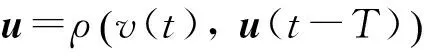
(52)

因?yàn)榫仃嘒是非滿秩的， 所以由(28)式確定的虛擬控制量v(t)到u的映射關(guān)系ρ并不是唯一的。 動態(tài)控制分配問題的最優(yōu)解可以通過如下二次規(guī)劃問題求解[12]：

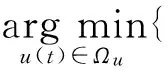
(53)

(54)

式中：us表示期望的穩(wěn)態(tài)輸入； 加權(quán)矩陣W1和W2是對稱正定的加權(quán)系數(shù)，Wv>0。W1表示u趨近于us的權(quán)重，W1越大，代表u能越精確收斂于期望穩(wěn)態(tài)值us。W2越大， 阻止u變化過快， 確保不會發(fā)生速率飽和。 加權(quán)系數(shù)矩陣Wv表示的是實(shí)際的控制量u和虛擬控制量v產(chǎn)生的控制效果一致性。 設(shè)矩陣W的表達(dá)式為

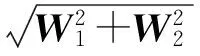
(55)

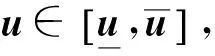
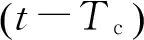
(56)

式中：

期望在穩(wěn)態(tài)導(dǎo)彈所需過載主要靠攻角提供。 當(dāng)攻角已經(jīng)建立起來后， 為了節(jié)省直接側(cè)向力資源， 導(dǎo)彈通過舵控制保持姿態(tài)穩(wěn)定。 根據(jù)式(1)， 可得系統(tǒng)的平衡狀態(tài)：

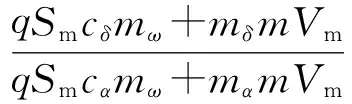
(57)

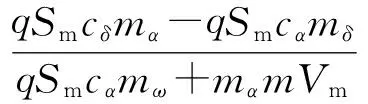
(58)

將式(57)～(58)代入到式(7)可得

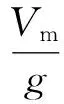
(59)

進(jìn)一步可以得到

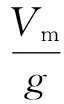
(60)

導(dǎo)彈的法向過載主要由攻角提供， 當(dāng)導(dǎo)彈跟蹤上過載指令后， 希望導(dǎo)彈姿態(tài)由氣動舵來控制， 即fye=0， 因此可以得到

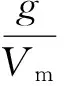
(61)

所以， 式(56)中， 期望的穩(wěn)態(tài)輸入為

(62)

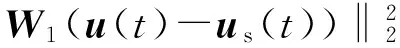
4 仿真分析

為了方便說明直接側(cè)向力和氣動舵配合產(chǎn)生的控制效果， 假設(shè)直接側(cè)向力是連續(xù)的， 先分析氣動舵和直接側(cè)向力分別單獨(dú)控制的情況。 從仿真結(jié)果圖1可以看出， 氣動舵負(fù)偏， 導(dǎo)彈抬頭建立正攻角， 產(chǎn)生正過載。 直接側(cè)向力作用效果剛好相反， 當(dāng)直接側(cè)向力為正， 導(dǎo)彈抬頭， 建立正攻角， 產(chǎn)生正過載。 也就是說， 建立正攻角時， 氣動舵負(fù)偏， 直接側(cè)向力為正， 這樣兩個執(zhí)行機(jī)構(gòu)產(chǎn)生的控制量沒有相互抵消的現(xiàn)象， 充分發(fā)揮控制效果。

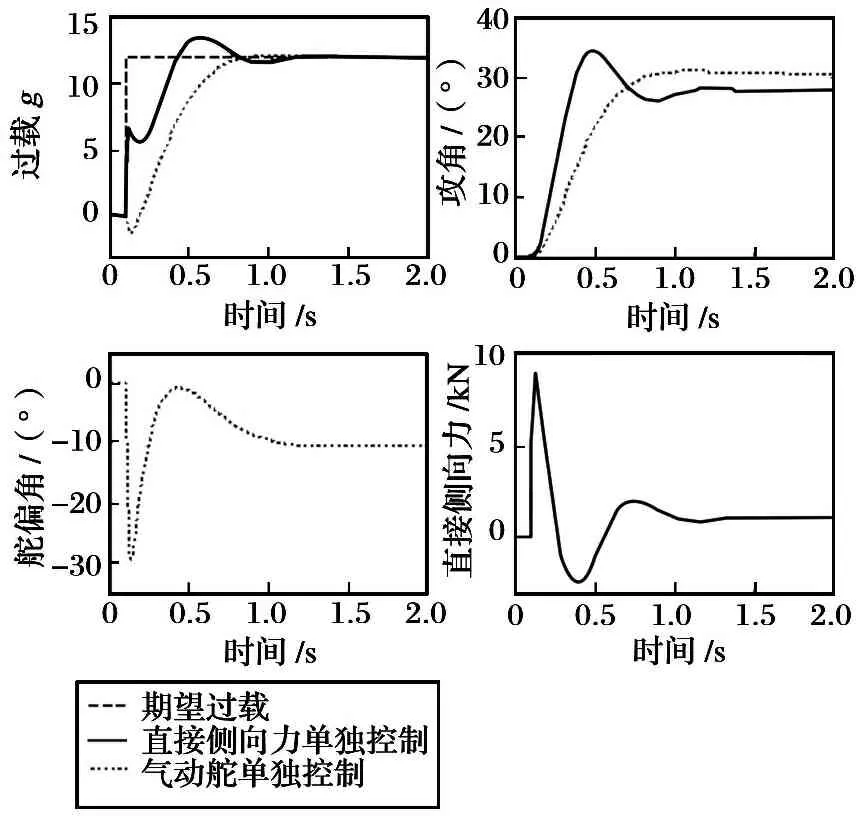
圖1 直接側(cè)向力和氣動舵單獨(dú)控制仿真結(jié)果

Fig.1 Simulation results for the missile purely controlled by direct lateral force and aerodynamic actuator

圖1顯示， 氣動舵單獨(dú)控制的情況下， 導(dǎo)彈具有明顯的非最小相位特性。 導(dǎo)彈過載響應(yīng)較慢， 過載上升時間為0.7 s左右。 氣動舵從0.2 s左右開始減速， 最后維持在-10°左右， 導(dǎo)彈保持30°的正攻角飛行。 當(dāng)直接側(cè)向力單獨(dú)控制時， 導(dǎo)彈控制系統(tǒng)是最小相位的。 導(dǎo)彈過載相應(yīng)比較快， 過載的上升時間為0.2 s左右。 直接側(cè)向力在0.25 s左右開始為負(fù)， 主要使導(dǎo)彈快速穩(wěn)定在期望攻角飛行。 最后， 直接側(cè)向力為正， 使得導(dǎo)彈維持正攻角飛行。 同時可以看出， 直接側(cè)向力單獨(dú)控制時， 導(dǎo)彈的攻角要小于氣動舵單獨(dú)控制時的情況， 主要是因?yàn)橹苯觽?cè)向力為正， 提供了一部分過載。

實(shí)際導(dǎo)彈側(cè)噴發(fā)動機(jī)具有非連續(xù)的工作特性， 這里采用向零取整的策略。 仿真結(jié)果如圖2所示。 從圖中可以看出， 復(fù)合控制情況下， 導(dǎo)彈過載響應(yīng)較快， 上升時間為0.2 s左右。 在導(dǎo)彈建立正攻角過程中， 氣動舵負(fù)偏， 直接側(cè)向力為正。 與圖1比較可見， 直接側(cè)向力和氣動舵相互配合建立攻角， 并且直接側(cè)向力不參與導(dǎo)彈攻角減速過程， 節(jié)省了脈沖發(fā)動機(jī)的使用量。 與文獻(xiàn)[4]的方法相比， 相同仿真條件下， 過載響應(yīng)上升時間相同， 本文提出的方法顯著節(jié)省了脈沖發(fā)動機(jī)點(diǎn)火數(shù)量， 并且過載響應(yīng)更平滑。

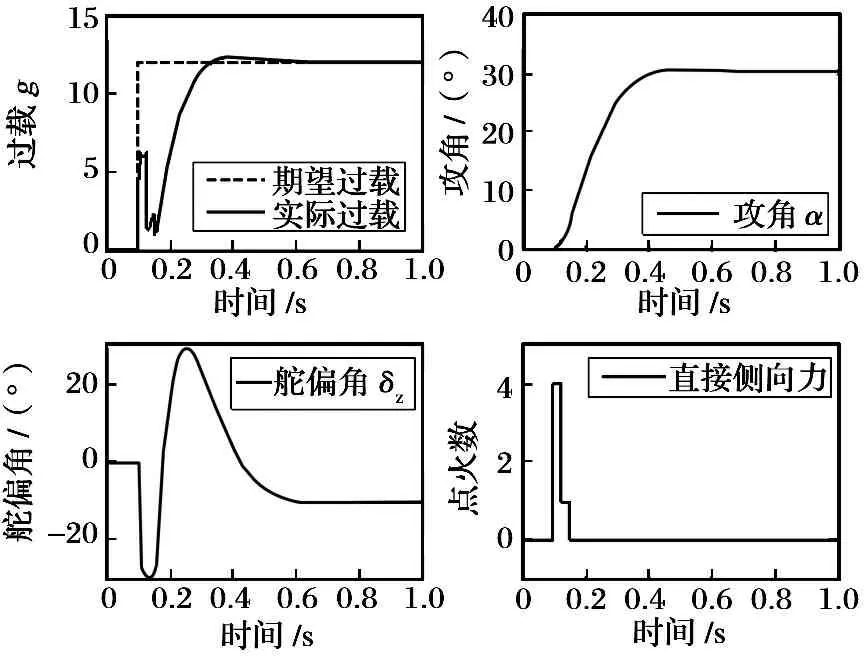
圖2 復(fù)合控制仿真結(jié)果

Fig.2 Simulation results for dual control systems

5 結(jié) 論

本文考慮了系統(tǒng)模型不確定性和外界干擾的影響， 研究了直接側(cè)向力與氣動力復(fù)合控制導(dǎo)彈自動駕駛儀設(shè)計問題。 對于擁有兩套執(zhí)行機(jī)構(gòu)的復(fù)合控制導(dǎo)彈， 將其自動駕駛儀設(shè)計過程分為兩步。 與傳統(tǒng)動態(tài)面方法相比， 設(shè)計過程中根據(jù)Lyapunov穩(wěn)定理論引入了自適應(yīng)參數(shù)估計算法， 設(shè)計了導(dǎo)彈虛擬控制律， 然后通過動態(tài)控制分配算法將虛擬控制律產(chǎn)生的控制量分配給實(shí)際執(zhí)行機(jī)構(gòu)。 針對復(fù)合控制導(dǎo)彈控制系統(tǒng)， 提出了一種動態(tài)控制分配參數(shù)設(shè)計方法。 從仿真結(jié)果來看， 本文提出的方法過載跟蹤快速且平穩(wěn)。 過載跟蹤過程中， 直接側(cè)向力與氣動舵相互配合， 節(jié)省了脈沖發(fā)動機(jī)的使用量。

[1] Xu Biao, Zhou Di, Liang Zhuo, et al. Robust Adaptive Sliding Sector Control and Control Allocation of a Missile with Aerodynamic Control Surfaces and Reaction Jets[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2017, 231(3): 397-406.

[2] Wise K A, Broy D J. Agile Missile Dynamics and Control[J]. Journal of Guidance, Control, and Dynamics, 1998， 21(3): 441-449.

[3] 周荻, 邵春濤. 大氣層內(nèi)攔截彈直接側(cè)向力/氣動力混合控制系統(tǒng)研究[J]. 宇航學(xué)報, 2007, 28(5):1205-1209. Zhou Di, Shao Chuntao. Hybrid Control System Design for an Atmospheric Interceptor Controlled by Lateral Jet Thrusters and Aerodynamic Surfaces[J]. Journal of Astronautics, 2007, 28(5): 1205-1209. (in Chinese)

[4] Thukral A, Innocenti M. A Sliding Mode Missile Pitch Autopilot Synthesis for High Angle of Attack Maneuvering[J]. IEEE Transactions on Control Systems Technology, 1998, 6(3): 359-371.

[5] Chang Yafei, Yuan Ruyi, Tan Xiangmin, et al. Observer-Based Adaptive Sliding Mode Control and Fuzzy Allocation for Aero and Reaction Jets Missile[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2016, 230(6): 498-511.

[6] Tournes C H, Shtessel Y B, Shkolnikov I. Missile Controlled by Lift and Divert Thrusters Using Nonlinear Dynamic Sliding Manifolds[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(3): 617-625.

[7] Li Quan, Zhou Di. Nonlinear Autopilot Design for Interceptors with Tail Fins and Pulse Thrusters viaθ-DApproach[J]. Journal of Systems Engineering and Electronics, 2014, 25(2): 273-280.

[8] 趙明元, 魏明英, 何秋茹. 基于有限時間穩(wěn)定和Backstepping的直接力/氣動力復(fù)合控制方法[J]. 宇航學(xué)報, 2010, 31(9): 2157-2164. Zhao Mingyuan, Wei Mingying, He Qiuru. Research on Method of Lateral Jet and Aerodynamic Fins Compound Control Based on Finite Time Stability and Backstepping Approach[J]. Journal of Astronautics, 2010, 31(9): 2157-2164.(in Chinese)

[9] Zhou Di, Shao Chuntao. Dynamics and Autopilot Design for Endoatmospheric Interceptors with Dual Control Systems[J]. Aerospace Science and Technology, 2009, 13(6): 291-300.

[10] 胥彪, 周荻. 受輸入飽和約束的導(dǎo)彈直接側(cè)向力/氣動力復(fù)合控制[J]. 宇航學(xué)報, 2012, 33(11): 1630-1635. Xu Biao, Zhou Di. Dual Aero/Propulsive Missile Control Subject to Input Saturation[J]. Journal of Astronautics, 2012, 33(11): 1630-1635. (in Chinese)

[11] Johansen T A, Fossen T I. Control Allocation—A Survey[J]. Automatica, 2013, 49(5): 1087-1103.

[12] H?rkeg?rd O. Dynamic Control Allocation Using Constrained Quadratic Programming[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(6): 1208-1034.

[13] Cui Lei, Yang Ying. Disturbance Rejection and Robust Least-Squares Control Allocation in Flight Control System[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(6): 1632-1643.

[14] Xing Lidan, Zhang Ke′nan, Chen Wanchun, et al. Optimal Control and Output Feedback Considerations for Missile with Blended Aero-Fin and Lateral Impulsive Thrust[J]. Chinese Journal of Aeronautics, 2010, 23(4): 401-408.

[15] Ridgely D B, Drake D, Triplett L, et al. Dynamic Control Allocation of a Missile with Tails and Reaction Jets[C]∥AIAA Guidance, Navigation and Control Conference and Exhibit, South Carolina, 2007: 1-32.

[16] 胥彪, 周荻. 基于反步法及控制分配的導(dǎo)彈直接側(cè)向力/氣動力復(fù)合控制[J]. 系統(tǒng)工程與電子技術(shù), 2014, 36(3): 527-531. Xu Biao, Zhou Di.Backstepping and Control Allocation for Dual Aero/Propulsive Missile Control[J]. Systems Engineering and Electronics, 2014, 36(3): 527-531.(in Chinese)

[17] Swaroop D, Hedrick J K, Yip P P, et al. Dynamic Surface Control for a Class of Nonlinear Systems[J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1893-1899.

AgileMissileAutopilotDesignviaAdaptiveDynamicSurfaceControlandControlAllocation

RenGaofeng1,XuBiao2,ZhangJinpeng1,3

(1.ChinaAirborneMissileAcademy，Luoyang471009，China； 2.CollegeofAstronautics,NanjingUniversityofAeronauticsandAstronautics，Nanjing210016，China； 3.AviationKeyLaboratoryofScienceandTechnologyonAirborneGuidedWeapons，Luoyang471009，China)

Based on adaptive dynamic surface control theory and dynamic control allocation algorithm, an autopilot design method is proposed for agile missiles with direct lateral force and aerodynamic force compound control. Actuators employed in agile missiles including lateral jet engine and actuator. In order to improve the control efficiency of agile missile with dual actuators, the autopilot system design process is divided into virtual control law design and the control allocation algorithm design. To deal with the system model uncertainties and external disturbances, the virtual control law is designed via dynamic surface control method and adaptive control method. Then the virtual control signal is distributed by control allocation method to the actual actuator. Simulation results show that missile autopilot system tracks the acceleration command fast and smoothly. In the tracking process, lateral jet engine cooperates with actuator, and the two actuators fully develop their actions.

missile； autopilot； dynamic surface control； adaptive control； control allocation

10.19297/j.cnki.41-1228/tj.2017.04.006

2017-04-10

國家自然科學(xué)基金項(xiàng)目(61603183)； 航空科學(xué)基金項(xiàng)目(20160152002)

任高峰(1983-)， 男， 河南鄭州人， 博士， 研究方向是導(dǎo)彈制導(dǎo)與控制。

任高峰， 胥彪， 張金鵬 . 基于自適應(yīng)動態(tài)面及控制分配的敏捷導(dǎo)彈自動駕駛儀設(shè)計[ J]. 航空兵器， 2017( 4): 33-39. Ren Gaofeng, Xu Biao, Zhang Jinpeng. Agile Missile Autopilot Design via Adaptive Dynamic Surface Control and Control Allocation[ J]. Aero Weaponry, 2017( 4): 33-39.( in Chinese)

TJ765

： A

： 1673-5048(2017)04-0033-07