基于高階滑模觀測器的微分滑模四旋翼無人機控制研究

魏炳翌， 聞 新

(南京航空航天大學 航天學院， 南京 210016)

基于高階滑模觀測器的微分滑模四旋翼無人機控制研究

魏炳翌， 聞 新

(南京航空航天大學 航天學院， 南京 210016)

針對四旋翼無人機魯棒控制問題， 提出了一種基于高階滑模觀測器的內環與外環控制器設計方法。 首先， 建立了四旋翼無人機模型的運動學與動力學方程， 通過反饋線性技術將模型分解為線性部分與非線性部分。 然后， 在輸入信號延遲的基礎上推導了相應的滑模控制律， 由分離定理分別設計了觀測器與控制器， 通過擾動識別減少需要觀測的狀態變量， 繼而減少了測量傳感器， 同時對觀測器以及整個閉環系統穩定性進行了證明。 仿真驗證了所提出的控制算法在提高四旋翼無人機姿態控制系統精度以及魯棒性方面的有效性。

四旋翼無人機； 姿態控制； 滑模微分； 高階滑模觀測器

0 引 言

四旋翼平臺具有空中懸停、 垂直起降和低速飛行的優勢， 但是， 其動力學模型具有非線性與欠驅動的特點， 同時， 各種不確定性外部擾動的存在以及四旋翼參數不確定和動態情況難以建模， 使得其姿態控制變得異常復雜。 四旋翼無人機控制系統設計要解決的關鍵問題是抑制上述非線性、 不確定性和外部干擾對系統性能的影響。

反饋線性化技術是解決動態特性、 未知參數和外部擾動的有效方法[1]， 然而， 其需要所有狀態變量的信息， 這一點限制了反饋線性化技術的實際應用。 對于四旋翼無人機系統， 即使可以測量所有的狀態量， 但往往帶有噪聲。 此外， 要測量所有的狀態量， 就需要更多的傳感器[2]， 無形中提高了系統的成本與難度。 為了減少測量傳感器， 文獻[2]提出了使用一個旋轉運動測量儀來達到對傾斜角度的控制和平移運動的跟蹤。

針對此類問題， 本文在四旋翼無人機模型反饋線性化的基礎上， 提出一種滑模狀態觀測器設計方法[3]。 滑模觀測器被廣泛應用， 因為其具有諸多優勢：(1)滑模觀測器對于系統未知輸入具有不敏感性， 比魯棒性更強； (2)通過將等效輸出反饋至系統輸入來識別未知變量； (3)狀態變量實際值有限時間內收斂。 觀測器設計時， 應用高階滑模算法， 通過任意階魯棒微分器[4-6]設計， 確保有限時間內一階狀態變量均收斂。 在文獻[7-8]中提出了二階滑模Super-Twisting算法， 機械系統觀測器僅需要對位移進行測量， 從而獲知速度與不確定度。 由于四旋翼無人機模型未知輸入相應階為2或4， 所以不滿足觀測系統未知輸入中不存在一階變量的充要條件[9]。 為了解決以上問題， 在高階滑模觀測器中要應用高階滑模微分技術[7]。

狀態觀測器不僅在系統監控和調度方面具有優勢， 而且可以檢測和識別動態系統故障。 觀測器的設計都是基于數學模型平臺， 而模型普遍不是線性化的， 并且具有未知輸入。 另一方面， 數學模型平臺的準確程度嚴重依賴已知輸出[3]。

本文建立四旋翼無人機模型的運動學與動力學方程， 將模型分解為線性與非線性部分， 推導出相應的滑模控制律， 避免觀測器中三階微分狀態量的出現。 在遇到外部擾動時， 通過控制器對系統進行補償。 外環控制器設計過程中， 通過擾動的識別減少觀測的狀態變量。 最后， 仿真驗證四旋翼無人機姿態控制在系統精度以及魯棒性方面的作用。

1 四旋翼無人機模型及問題描述

1.1 四旋翼無人機模型

本文采用文獻[10]描述的四旋翼無人機模型， 飛行時四個旋翼分為兩組， 斜對角旋翼為一組， 每組旋轉方向相同， 不同組旋翼旋轉方向相反， 旋翼提供操縱力和扭矩， 建立面向控制的數學模型時考慮如下假設[11]：

(1) 忽略地球自轉角速度， 因其相比于四旋翼的旋轉運動慢得多；

(2) 假設四旋翼的質心、 重心與形心在同一點。

先定義兩個框架： 地球慣性坐標系與機體自身坐標系。 在機體自身坐標系下可以更好地確定運動方程， 慣性矩陣在機體系下是不變的， 利用四旋翼對稱性可以簡化方程， 飛行中的測量值可以更方便地在機體坐標系中表達。

定義ζ=[ψ，θ，φ]T∈R3和ω=[p，q，r]T， 其中φ，θ，ψ是地球慣性坐標系下的偏航角、 俯仰角和滾轉角；p，q，r是機體坐標系滾轉、 俯仰和偏航角速度。

(1)

(2)

根據文獻[10]，RΘ和ω的關系可表示為

(3)

(4)

四旋翼模型動力學方程為

(5)

(6)

由于之前的假設條件， 四旋翼模型[10]的耦合慣量為0， 慣性矩陣I=diag(Ix，Iy，Iz)，Ix，Iy，Iz為機體自身坐標系下關于x，y，z軸的轉動慣量。F，Tx,Ty,Tz代表額外的力和轉矩， 是由無人機的重量、 空氣動力矩陣和旋翼提供的推力、 轉矩組成， 具體形式如下：

(7)

本文中所有類似表達均為此含義，cφ=cosφ，cψ=cosψ，sθ=sinθ,sφ=sinφ,sψ=sinψ,cθ=cosθ,seθ=secθ。

式中：[Qx，Qy，Qz]T與[Qp，Qq，Qr]T是四旋翼無人機受到的氣動力和氣動力矩；g是重力常數；d是質心到旋翼之間的距離。 控制輸入u1是全體旋翼推力，u2是左右旋翼推力差，u3是前后旋翼推力差，u4兩組旋翼扭矩差[10]。

1.2 反饋線性化與內環控制器

針對四旋翼無人機欠驅動的特點， 運用反饋線性化技術設計內環和外環控制器。內環控制器使用全狀態反饋， 對部分非線性的動態輸出線性化， 本文將非線性系統分成線性部分和非線性部分， 其中非線性部分為Brunovsky標準型[12]。 控制輸入u1，u2，u3，u4， 需要用新的控制輸入q1，q2，q3，q4代替， 以避免在精確線性化時變換矩陣變得不可逆。 這樣， 使用雙積分器使u延遲[13]：

(8)

將式(6)～(7)改寫為MIMO仿射非線性系統的形式：

(9)

其中，x=[x，y，z，ψ，θ，φ，u0，v0，ω0，ζ，ξ，p，q，r]T；y=[x，y，z，ψ]T；x，y，z為地球坐標系下的位置坐標；ψ，θ，φ為地球坐標系下的角度坐標。

(10)

(11)

通過計算可得det(φ(x))≠0，φ(x)可逆， 可以保證控制狀態受到系統輸入信號的有效控制。

(12)

系統(9)關于輸出量的相對階r1+r2+r3+r4=14與系統的階數相等， 所以系統可以完全線性與可控化， 但由于外部環境多變， 飛行參數存在不確定性以及外部擾動等原因， 導致輸入輸出反饋線性化過程不精確， 這時利用式(10)控制律可以將系統解耦為線性部分和非線性擾動部分。

(13)

式中：vi，i=1, 2, 3, 4是最終控制信號， 需要設計系統外環控制器將系統控制狀態的初始狀態和其連續導數擬合成需要的狀態軌跡。

2 控制器設計

本文采用的高階滑模控制器[14-15]具有時間收斂的特性， 滿足分離定理條件。 因此， 控制器設計可與觀測器設計分開。

四旋翼無人機線性動態模型測量信號分為位置測量信號x1=[x，y，z]T與角度測量信號x5=4， 表達成狀態空間模型為

(14)

(15)

其中，

(16)

(17)

式中:ci為觀測器對控制量的補償值；α1,α2為補償系數。

2.1 線性反饋外環控制器設計

前文構造了新的輸入控制信號， 需要建立一個多項式控制律來適應新的輸入量v， 同時對非線性干擾進行補償：

(18)

(19)

(20)

(21)

2.2 高階滑模觀測器設計

(22)

引理1 參數選擇條件為在輸入誤差出現后的瞬間， 即在有限時間內， 符合如下方程：

(23)

引理2 噪聲滿足如下不等式：

(24)

在有限時間內建立不等式， 正常數μi，vi取決于微分參數ε：

(25)

引理3 噪聲引入后的連續輸入采樣間隔τ>0， 在有限時間內建立不等式， 正常數μi，vi僅僅取決于微分參數τ：

(26)

系統n階微分誤差與τ成正比， 所以在n階內要建立相同個數的滑動模型。

2.3 外環控制器輸出狀態重構

上節建立的滑模觀測器， 事實上是一個狀態估計器， 在估計狀態量中只包含部分輸入變量x，y，z，ψ。 因為估計狀態量不包括所有的輸入變量， 要想完成所有的狀態輸出估計， 必須考慮之前忽略的輸入變量θ，φ，p，q，r， 從而需要構造新的狀態變量。

在不考慮擾動情況下，θ，φ，p，q，r的觀測值通過非線性系統式(9)計算得出。 計算θ和φ觀測值如下[19]：

(27)

(28)

引理4[20]根據定理1中的方法， 系統(9)中的高階滑模觀測器， 假設系統狀態和控制量有界且Lebesgue可測， 則通過選擇合適的參數γ1=3，γ2=2.5，γ3=γ4=1.5， 通過x1，x2，x3，x4，x5，x6， 可使得狀態觀測量以及相應擾動在有限時間內收斂到其真實值。

綜上， 新的狀態觀測量與定理1中x1，x2，x3，x4，x5，x6組成了系統所有的狀態量， 且相應的非線性部分均可微并且趨向于0， 則整個閉環系統的穩定性得證。

3 仿真驗證

以某四旋翼無人機為例進行姿態控制系統的數值仿真試驗。 仿真中，m=1 kg，Ix=Iy=0.008 1 kg·m2；Iz=0.014 2 kg·m2；g=9.81 m/s2。

Qx，Qy，Qz與Qp，Qq，Qr是四旋翼無人機的氣動力與氣動轉矩， 可以通過氣動系數Ci得到：

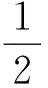
(29)

式中：ρ為無人機所處環境大氣密度；W是空氣與無人機的相對速度； 氣動系數Ci與空氣速度和機體坐標間的夾角有關， 也與機體與旋翼的氣動力有關。

為了驗證高階滑模觀測器的魯棒性， 建立以下三種狀況。

Case 1： 沒有外界擾動的情況，Qx，Qy，Qz，Qp，Qq，Qr均為0， 其結果如圖1～2所示。

圖1 3D跟蹤控制仿真結果

Fig.1 Three-dimentional tracking-control simulation results

圖2X軸跟蹤控制仿真結果

Fig.2 Tracking-control simulatiom results ofX-axis

Case 2： 在氣動力干擾條件下， 其中

(30)

發生在0 s， 20 s時， 其結果如圖3～4所示。

圖3 Case 2位置坐標仿真結果

圖4 Case 2位置坐標微分量仿真結果

Fig.4 Coordinates microcomponent simulation results in Case 2

Case 3： 在Case 2的基礎上添加劇烈隨機氣動力干擾， 其中Qx1是均值為0， 方差為2的隨機信號；Qy1是均值為0， 方差為0.1的隨機信號；Qz1=0。

(31)

圖2是高階滑模對四旋翼X軸位移跟蹤控制仿真結果。 可以看出， 在沒有任何干擾的情況下， 高階滑模觀測器表現出了令人滿意的結果。

圖3是狀態變量在氣動力和力矩干擾下變化情況， 在擾動發生之后有限的時間內迅速收斂， 表明了觀測器的有效性。 在圖4中也可以得出同樣的結論， 狀態變量的一階導數在有限時間內趨于0， 并且消失， 表現出了觀測器與控制器的魯棒性。

圖5在Case 3情況下， 四旋翼無人機角度坐標發生的變化， 而圖6是角度微分量發生的變化。 由此可知， 在隨機擾動發生以后系統可以在有限時間內收斂， 但會產生震蕩， 表明高階微分滑模處于劇烈隨機擾動之中， 不能精確地跟蹤系統。

圖5 Case 3角度坐標仿真結果

圖6 Case 3角度坐標微分量仿真結果

Fig.6 Angle coordinate microcomponent simulation results in Case 3

4 結 論

本文針對四旋翼無人機姿態控制系統設計問題， 在四旋翼無人機模型反饋線性化的基礎上， 設計了一種基于高階滑模觀測器的全狀態內環控制器。 外環控制器的設計過程中， 通過擾動識別減少需要觀測的狀態變量。 最后， 以某四旋翼無人機為例， 考慮氣動力與氣動力矩擾動的情況。 數值仿真表明： 本文所提出的觀測器與控制器設計具有較強的魯棒性， 且有效地提高系統精度； 添加隨機擾動之后， 系統仍然可以保持一定的穩定性， 但是會產生小幅震蕩， 這將是未來的研究方向。

[1] Slotine J E， Hedrick J K. Robust Input-Output Feedback Linearization[J]. International Journal of Control， 1993， 57(5): 1133-1139.

[2] Mokhtari A， Benallegue F A. Dynamic Feedback Controller of Euler Angles and Wind Parameters Estimation for a Quadrotor Unmanned Aerial Vehicle[C]∥ IEEE International Conference on Robotics and Automation， 2004: 2359-2366.

[3] Levant A. Sliding Order and Sliding Accuracy in Sliding Mode Control[J]. International Journal of Control， 1993， 58(6): 1247-1263.

[4] Levant A. Robust Exact Differentiation via Sliding Mode Technique[J]. Automatica， 1998， 34(3): 379-384.

[5] Levant A. Higher-Order Sliding Modes， Differentiation and Output-Feedback Control[J]. International Journal of Control， 2003， 76(9): 924-941.

[6] Hautus M L J. Strong Detectability and Observers[J]. Linear Algebra & Its Applications， 1983， 50(APR): 353-368.

[7] Davila J， Fridman L， Poznyak A. Observation and Identification of Mechanical Systems via Second Order Sliding Modes[J]. International Journal of Control， 2006， 79(10): 1251-1262.

[8] Davila J， Fridman L， Levant A. Second-Order Sliding-Mode Observer for Mechanical Systems[J]. IEEE Transactions on Automatic Control， 2005， 50(11): 1785-1789.

[9] Wang W， Gao Z. A Comparison Study of Advanced State Observer Design Techniques[C]∥ Proceedings of the IEEE American Control Conference. 2003: 4754-4759.

[10] Abdolhosseini M， Zhang Y M， Rabbath C A. An Efficient Model Predictive Control Scheme for an Unmanned Quadrotor Helicopter[J]. Journal of Intelligent & Robotic Systems， 2013， 70(1-4): 27-38.

[11] Soest W R V， Chu Q P， Mulder J A. Combined Feedback Linearization and Constrained Model Predictive Control for Entry Flight[J]. Journal of Guidance, Control, and Dynamics， 2006， 29(2): 427-434.

[12] Gardner R B， Shadwick W F. The GS Algorithm for Exact Linearization to Brunovsky Normal Form[J]. IEEE Transactions on Automatic Control， 1992， 37(2): 224-230.

[13] Raumer T V， Dion J M， Dugard L， et al. Applied Nonlinear Control of an Induction Motor Using Digital Signal Processing[J]. IEEE Transactions on Control Systems Technology， 1994， 2(4): 327-335.

[14] Iqbal S， Edwards C， Bhatti A I. Robust Feedback Linearization Using Higher Order Sliding Mode Observer[C]∥2011 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC), 2011: 7968-7973.

[15] Davila J， Fridman L， Levant A. Second-Order Sliding-Mode Observer for Mechanical Systems[J]. IEEE Transactions on Automatic Control， 2005， 50(11): 1785-1789.

[16] Ahmed-Ali T， Lamnabhi-Lagarrigue F. Sliding Observer-Controller Design for Uncertain Triangular Nonlinear Systems[J]. IEEE Transactions on Automatic Control， 1999， 44(6): 1244-1249.

[17] Slotine J J E， Hedrick J K， Misawa E A. On Sliding Observers for Nonlinear Systems[J]. Journal of Dynamic Systems, Measurement and Control， 1986， 109(3): 245-252.

[18] Utkin V I. Sliding Modes in Control and Optimization[J]. Communications & Control Engineering， 1992, 189(3): 1372.

[19] Tran X T, Kang H J. Adaptive hybrid High-Order Terminal Sliding Mode Control of MIMO Uncertain Nonlinear Systems and Its Application to Robot Manipulators[J]. International Journal of Precision Engineering and Manufacturing, 2015, 16(2): 255-266.

[20] Benallegue A, Mokhtari A, Fridman L. High-Order Sliding-Mode Observer for a Quadrotor UAV[J]. International Journal of Robust & Nonlinear Control, 2010, 18(4-5): 427-440.

StudyonSliding-ModeDifferentiationQuadrotorUAVBasedonHigh-OrderSliding-ModeObserver

WeiBingyi，WenXin

(CollegeAstronautics，NanjingUniversityofAeronauticsandAstronautics，Nanjing210016，China)

Aiming at the problem of robust control of quadrotor UAV， a sliding mode controller design method based on high order sliding-mode observer is proposed. Firstly， the kinematics and dynamics equations of the quadrotor UAV model are built， and the model by using the feedback linearization techno-logy is decomposed into linear part and nonlinear part， then， the corresponding sliding mode control law is derived on the basis of the delay of the input signal. The observer and the controller are designed separately by the separation theorem. The state variables which need to be observed are reduced by disturbance identification， then the sensors are reduced， and the stability of the whole closed loop system and the observer is proved. The simulation results show that the proposed control algorithm can improve the attitude control accuracy and robustness of the quadrotor UAV.

quadrotor UAV； attitude control； sliding-mode differentiation； high-order sliding-mode observer

10.19297/j.cnki.41-1228/tj.2017.04.005

2016-10-25

魏炳翌(1993-)， 男， 山西晉中人， 碩士研究生， 研究方向為故障診斷與容錯控制。

魏炳翌， 聞新 . 基于高階滑模觀測器的微分滑模四旋翼無人機控制研究[ J]. 航空兵器， 2017( 4)： 26-32. Wei Bingyi, Wen Xin. Study on Sliding-Mode Differentiation Quadrotor UAV Based on High-Qrder Sliding-Mode Observer[ J]. Aero Weaponry, 2017( 4): 26-32.( in Chinese)

V249.122

： A

： 1673-5048(2017)04-0026-07