基于Jones-Nelson本構模型的C/C復合材料喉襯變形研究①

陳天宇，史宏斌，唐 敏，李 耿，許承海

(1.中國航天科技集團公司四院四十一所，西安 710025；2.哈爾濱工業大學 復合材料與結構研究所,哈爾濱 150001)

基于Jones-Nelson本構模型的C/C復合材料喉襯變形研究①

陳天宇1，史宏斌1，唐 敏1，李 耿1，許承海2

(1.中國航天科技集團公司四院四十一所，西安 710025；2.哈爾濱工業大學 復合材料與結構研究所,哈爾濱 150001)

引入了應力-應變關系擴充理論和加權柔度修正理論，修正了Jones-Nelson本構模型，建立了基于Jones-Nelson模型的C/C復合材料本構關系，使得該模型可在考慮材料各向異性、拉壓雙模量、損傷演化特征的情況下，用于表征任意拉壓混合載荷作用下的多向編織C/C復合材料的力學性能。在此基礎上，進行了C/C復合材料喉襯變形研究，同時展開了喉襯應變場的測試。結果表明，考慮Jones-Nelson模型的計算結果和測試結果更吻合。

喉襯;C/C復合材料;Jones-Nelson本構模型;加權柔度理論

0 引言

喉襯是固體火箭發動機的關鍵部件[1]，而其所處的熱力學環境十分惡劣[2]。因此，喉襯熱結構設計是發動機設計的重要內容。C/C復合材料由于較好的熱力學性能，廣泛用于大型固體火箭發動機喉襯結構[3]，但由于對該材料復雜的非均質特性認識不足，長期以來一直缺乏適合的本構模型，導致對喉襯應變場的計算結果誤差較大[4-8]。

Jones-Nelson本構模型是描述復合材料非線性本構關系的經典模型，前人通過對該模型的改進，研究了復合材料的力學行為。段登平等[9]通過對模型進行有效的擴展，使得該模型可用于研究大變形下非線性材料的力學性能，擴充了該模型的適用性，從而提高了材料性能的預報精度；譚慧豐等[10]引入復合材料大變形理論和變泊松比理論，通過選取適當的轉換點，對材料力學性能曲線進行線性擴展，使得非線性材料在大變形情況下，仍可通過Jones-Nelson本構模型進行求解；許承海、孟松鶴等在Jones-Nelson模型的改進與應用過程中，也起到了積極的作用。

本文通過多向編織C/C復合材料各向單軸拉伸、壓縮、剪切實驗，求得了該材料的Jones-Nelson本構模型的參數，同時引入應力-應變關系擴充理論和加權柔度修正理論，建立了多向編織C/C復合材料的Jones-Nelson本構模型修正模型，使得該模型可在考慮材料各向異性、拉壓雙模量、損傷演化特征的情況下，更好地表征多向編織C/C 復合材料的力學性能。并在此基礎上進行了C/C復合材料喉襯變形分析。開展了固體火箭發動機地面點火對比試驗。結果表明，修正的Jones-Nelson本構模型較好地反映了C/C復合材料的力學性能，考慮修正的Jones-Nelson本構模型的計算結果與實驗結果更加吻合。

1 C/C復合材料本構模型

1.1 C/C復合材料的正交各向異性柔度矩陣

本文研究的多向編織C/C復合材料，采用拉擠成型的剛性碳棒構成軸向網絡，軟炭纖維束編織成預制體，碳棒截面為圓形，炭纖維束截面為矩形。圖1為該材料的實物圖及空間結構圖。為了研究方便規定：與碳棒平行的面為面內，與碳棒垂直的面為面外。碳棒方向為軸向(1方向)，面外與炭纖維束同向為0°方向(2方向)，與炭纖維束垂直方向為90°方向(3方向)。

由材料空間結構圖不難看出，該材料的1方向-2方向平面、1方向-3方向平面及2方向-3方向平面都是材料的彈性對稱面。且上述3個彈性對稱面是相互正交的。因此，該材料是正交各向異性材料，適用于式(1)所示的正交各向異性柔度矩陣。

(1)

用廣義彈性模量Ei，泊松比μij和剪切模量Gij代替式(1)中各柔度分量，如式(2)所示。其中，由于在面內0°方向和90°方向的剪切模量G13和G23大小相當，因此在式(2)中，取G13=G23。在式(2)中，C/C復合材料的非線性參數E1、E2、E3、G13、G23、G12的取值將直接影響材料本構模型的精度。因此，需要選取合適的非線性本構模型計算這些參數。

(2)

在以往的非線性材料力學模型中(不考慮Jones-Nelson模型)，常取E2=E3=45 100 MPa，E1=52 600 MPa，G12=27 100 MPa，G13=G23=22 100 MPa 。μ12=μ21=μ13=μ31=0.06，μ23=μ32=0.28。然而，多向編織C/C復合材料的力學性能具有各向異性、拉壓雙模量、損傷演化特征等復雜的特性，式(2)僅能表現各向異性。為了更加準確地描述材料力學性能，需要引入Jones-Nelson本構模型。

1.2 Jones-Nelson本構模型

非線性材料中任何一種損傷形式的發生都將伴隨著應變能的不同變化和剛度的相應衰減，從而引起材料本構關系的非線性[11]。Jones和 Nelson根據材料彈性性能與應變能之間一一對應的關系，提出了如下的Jones-Nelson模型[12]：

Yi=Ai[1-Bi(U/U0)Ci]

(3)

式中Yi為材料的非線性力學性能, 通常是彈性模量或泊松比；Ai、Bi、Ci分別為第i條應力-應變曲線的初始斜率、初始曲率和初始曲率變化率；U為應變能密度，U0為使U/U0成為無量綱的一個常量。

該模型沒有限定非線性力學性能的個數和類型；公式中的應變能密度既沒有方向性，也與所選取的坐標系無關，形式簡明；可通過材料主軸方向上的單軸力學性能實驗建立材料在各方向上的本構關系，便于工程計算。從而廣泛用于各類復合材料非線性性能描述中。

2 Jones-Nelson本構模型的擴充與修正

2.1 Jones-Nelson模型的擴充

在計算中，Jones-Nelson本構模型存在一個限制條件：材料應變能密度必須小于材料的單向應變能密度極限。但對于高各向異性的復合材料來說，尤其是當該材料處于復雜載荷條件下時，由于材料存在損傷演化的過程，往往會出現強化現象，應變能密度往往會遠大于單軸的應變能密度極限。

為了應對這一現象，需對Jones-Nelson本構模型進行擴充。在材料進入損傷演化階段后，以應力-應變曲線的切線方向補充曲線，擴充理論示意圖如圖2(a)所示。由擴充模型的應力-應變曲線圖亦可得到Jones-Nelson本構模型擴充模型示意圖，如圖2(b)所示。

2.2 Jones-Nelson模型參數的修正

Jones-Nelson模型雖然可有效地解決材料的非線性問題，但考慮到C/C復合材料多表現為各向異性和拉壓雙模量的特點，僅利用該模型來計算材料的本構關系遠遠無法滿足工程需求。為此,本文通過對材料本構關系中的柔度矩陣進行加權修正。

加權柔度修正模型的主要內容包括：建立正交各向異性材料的柔度矩陣，再對Jones-Nelson模型中的應變能密度進行計算的方法實現，由此計算得到的應變能密度具有了方向性。用材料局部應力的正負性決定材料的局部柔度的方法體現材料的拉壓雙模量。

根據加權柔度修正模型的內容，已知材料局部應力的值為σ1、σ2、σ3，對材料的局部柔度做以下假設：

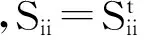
(4)

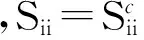
(5)

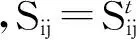
(6)

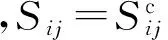
(7)

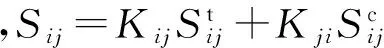
(8)

(9)

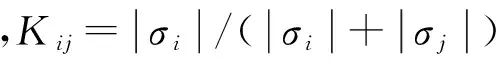
這種加權柔度矩陣，既保證了柔度矩陣的對稱性，也反映C/C復合材料各向異性、拉壓雙模量的特點，體現了不同加載路徑下的柔度變化，提高了Jones-Nelson本構模型在任意拉壓混合載荷作用下的計算精度。

2.3 Jones-Nelson模型參數的確定

通過對復合材料進行力學性能試驗，獲得材料各測點各向力學性能，再通過最小二乘法極值原理，對所有數據進行回歸擬合來確定參量Ai、Bi、Ci的值。由此得到的參數值誤差較小。

為此，開展了C/C復合材料單軸力學性能測試實驗。該實驗在室溫環境下進行，拉伸實驗采用INSTRON 5500R拉伸實驗機，壓縮實驗采用ASAN(MTS)858Mini Bionix壓縮實驗機，剪切實驗采用INSTRON 4505萬能實驗機。拉伸、壓縮實驗試樣應變的測量是通過儀器自帶的引伸計測定試樣表面應變來實現的。剪切實驗試樣應變的測量是通過應變片測定試樣表面的應變來實現的。

表1為運用材料各方向的單軸拉伸、壓縮、剪切實驗結果確定的修正Jones-Nelson模型參數。

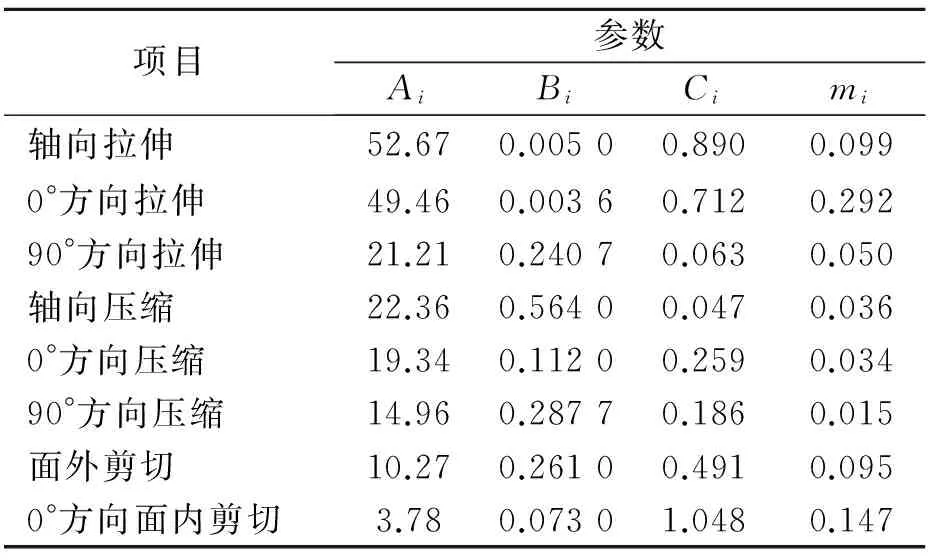
表1 Jones-Nelson模型參數

由表1可知，C/C復合材料的具有顯著的各向異性，拉壓雙模量特性，且材料損傷對于其力學性能的影響顯著。對Jones-Nelson模型進行擴充與加權修正十分必要。依據表1中的數據及2.1節、2.2節的內容建立多向編織C/C復合材料的Jones-Nelson模型，并編譯Fortran程序，用于ABAQUS的二次開發。

3 計算模型

3.1 有限元模型

固體火箭發動機噴管有限元模型如圖3所示。由于材料參數的不同，將噴管熱結構模型分為喉襯、擴張段、收斂段、背壁和2處外殼體共6部分，整體計算后，僅取喉襯部分計算數據做溫度場、應變場的研究。

在溫度場計算中，采用DC4X4線性完全積分四邊形單元，在應變場計算中，采用C4X4R雙線性減縮積分四邊形單元。

3.2 初始條件與邊界條件

在溫度場計算過程中，噴管初始溫度為20 ℃，燃燒室內壁面初始溫度為3200 ℃，燃燒室外壁面初始溫度為20 ℃。噴管入口處殼體法蘭盤沿軸向固定，噴管的外壁面處于絕熱狀態。

在應變場計算過程中，噴管的初始溫度根據溫度場計算結果設置預定義場，燃燒室內初始靜壓為6.37 MPa，噴管入口處殼體法蘭盤沿軸向固定。

3.3 溫度場結果與分析

圖4為20 s時刻喉襯部分的溫度云圖。從圖4可看到，最高溫度位于柱段入口處，為2554 ℃，最低溫度位于喉襯與背壁連接處，為477 ℃。

3.4 應變場結果與分析

在4.2 s時，應變片處溫度為126 ℃，已達到粘接膠失效發生收縮的臨界點。因此，應變場的仿真時間定為4.2 s，圖5為412 s時刻應變云圖。

圖5(a)為不考慮Jones-Nelson本構模型的4 s時刻噴管喉襯的軸向應變圖，4 s時刻軸向應變全部為正。最大應變位于喉襯內壁與收斂段連接處為2907 με，最小應變位于喉襯外壁與背壁連接處為81 με。

圖5(b)為考慮Jones-Nelson本構模型的4 s時刻噴管喉襯的軸向應變圖，4 s時刻軸向應變在喉襯內壁面為正，喉襯外壁面靠近背壁處為負。最大應變位于喉襯內壁面與收斂段連接處為3138 με，最小應變位于喉襯外壁面靠近背壁處為-37 με。圖5(c)為不考慮Jones-Nelson本構模型的4 s時刻噴管喉襯的環向應變圖，4 s時刻環向應變全部為正。最大應變位于喉襯內壁面與收斂段連接處為3747 με，最小應變位于喉襯外壁面與背壁連接處為666.8 με。圖5(d)為考慮Jones-Nelson本構模型的4 s時刻噴管喉襯的環向應變圖，4 s時刻環向應變全部為正。最大應變位于喉襯內壁面與收斂段連接處為6022 με，最小應變位于喉襯外壁面與背壁連接處為586.6 με。

4 實驗結果與討論

4.1 試驗用發動機及測點位置

試驗采用φ340 mm燒蝕試驗發動機，為了對比方便并減小工作量，同時不破壞實驗發動機本身的結構，在做實驗過程中，僅取一個應變測點提取數據。為方便給應變片定位，特取xoy坐標系，坐標系及測點位置如圖6所示。應變片編號、分布如表2所示。

4.2 應變場測試結果及分析

如圖7(a)所示，軸向應變實驗曲線連續性較好。S1所在處的最高應變出現在3.87 s，為916.20 με。在不考慮Jones-Nelson本構模型的計算中，3.87 s時刻軸向應變達到992.4 με，與實驗數據平均值的誤差為8.3%。在考慮Jones-Nelson本構模型的計算中，3.87 s時刻軸向應變達到894.3 με，與實驗數據平均值的誤差為2.0%。

如圖7(b)所示，環向應變實驗曲線連續性與一致性較好。S2所在處的最高應變出現在3.89 s，為844.64 με。在不考慮Jones-Nelson本構模型的計算中，3.89 s時刻環向應變達到644.1 με，與實驗數據平均值的誤差為23.6%。在考慮Jones-Nelson本構模型的計算中，3.89 s時刻環向應變達到802.8 με，與實驗數據平均值的誤差為4.9%。

坐標/cm應變測點編號軸向環向(91,45)S1S2

5 結論

(1)在Jones-Nelson模型的基礎上，通過應力-應變曲線擴充理論和加權柔度修正理論，對模型進行了擴充和修正，使得該模型可在考慮材料各向異性、拉壓雙模量、損傷演化特征的情況下，用于表征復雜載荷條件下多向編織C/C復合材料的力學性能，從而建立了多向編織C/C復合材料的本構模型。

[1] 李江，何國強，陳劍，等.高過載條件下絕熱層燒蝕實驗方法研究(II)收縮管聚集法[J].推進技術，2004,25(3):196-198.

[2] 劉洋，何國強，李江，等.聚集狀態下凝相顆粒的收集與測量[J].推進技術, 2005，26(3):447-480.

[3] 李江，婁永春，劉洋，等.聚集狀態對固體火箭發動機顆粒粒度分布的影響[J].固體火箭技術,2005,28(4):265-267.

[4] 張勝敏，胡春波，徐義華.固體火箭發動機燃燒室凝相顆粒燃燒特性分析[J].固體火箭技術,2010,33(3):256-259.

[5] Averin V S,Arkhipov V A,Vasenin I M,et al. Effect of a sudden change in cross-sectional area of the solid rocket motor duct on coagulation of condensed particles[J].Combustion,Explosion,and Shock Waves,2003,39( 3):316-322．

[6] 田維平，許團委，王建儒. 過載下燃燒室粒子特性與絕熱層燒蝕研究進展[J].固體火箭技術，2015,38(1):30-36.

[7] 許宏濤，陳林泉. 固體火箭發動機燃燒室內粒子取樣方法研究[D].西安：航天動力技術研究院，2007.

(編輯：崔賢彬)

Analysis of C/C composites throat distortionbased on the Jones-Nelson constitutive model

CHEN Tian-yu1,SHI Hong-bin1,TANG Min1,LI Geng1,XU Cheng-hai2

(1.The 41st Institute of the Fourth Academy of CASC,Xi'an 710025,China;2.Center for Composite Materials and Structure,Harbin Institute of Technology,Harbin 150001,China)

Imports the extension theory of stress-strain relation and weighted slenderness theory,modifies Jones-Nelson constitutive model,establishes the constitutive relationship of carbon/carbon composites based on the Jones-Nelson model,to express the material elastic constants accurately in any tension and compression of mixed loading. Based on the study,analyzes the distortion of the C/C composites throat,texted on the throat strain field at the same time.The results show that the simulation results which considering the Jones-Nelson model coincide to the experiment results.

throat;carbon/carbon composites;Jones-Nelson constitutive model;weighted slenderness theory

2016-05-19；

2016-08-25。

陳天宇(1990—),男,碩士,研究方向為工程力學。E-mail：2219514790@qq.com

V435+.3

A

1006-2793(2017)04-0414-06

10.7673/j.issn.1006-2793.2017.04.003