基于NHDO的機動目標攔截攻擊角度約束導引律①
王 斌,雷虎民,李 炯,邵 雷,葉繼坤
(空軍工程大學 防空反導學院,西安 710051)
基于NHDO的機動目標攔截攻擊角度約束導引律①
王 斌,雷虎民,李 炯,邵 雷,葉繼坤
(空軍工程大學 防空反導學院,西安 710051)
為了精確控制導彈在有限時間內以期望攻擊角度攔截機動目標,采用將導彈自動駕駛儀簡化為慣性環節的方法,結合終端滑模控制理論設計了一種帶攻擊角度約束的有限時間收斂制導律。為了濾除視線角速率噪聲,提出一種非線性跟蹤微分濾波器對噪聲進行濾波,建立了考慮濾波的制導系統狀態方程,基于此方程設計非齊次干擾觀測器,用于目標機動不確定項的估計補償。仿真結果表明,所設計的制導律能達到對視線角速率有效濾波,對目標機動狀態精確估計的目的,克服系統動態延遲對制導精度的不利影響,滿足攻擊角度和制導精度的雙重要求。
攻擊角度約束;有限時間收斂;跟蹤微分濾波器;非齊次干擾觀測器;制導律
0 引言
導彈作為現代戰爭的主要作戰武器,其制導精度始終是人們努力追求的優化目標,而以零化脫靶量為主要目的傳統制導武器已不能滿足最佳打擊效果的戰術要求。為取得最佳打擊效果,最大程度地擊毀目標,必須在高精度制導的同時考慮導彈命中目標時的姿態問題,即攻擊角度約束問題[1]。無論是反艦導彈飽和攻擊,還是反導攔截協同作戰,都要求攔截彈從不同的方向以一定的攻擊角度擊中目標。因此,開展帶攻擊角度約束的制導方法研究具有現實而緊迫的意義。
伴隨控制理論的不斷發展,攻擊角度約束的導引律(IACG)研究已經取得一系列豐碩成果。文獻[2-3]討論了一類兩階段控制的偏置比例導引律,用于攻擊固定目標和非機動運動目標;文獻[4]針對固定目標,提出一種時變比例導引系數的IACG;文獻[5]將文獻[4]的方案進一步改進,使其擴展到非機動運動目標的攔截上;文獻[6]設計了一種虛擬角度控制項,將攻擊角度控制問題轉化為該虛擬量的收斂問題。上述導引律雖然實現了對攻擊角度的精確控制,但只適合于攔截非機動目標,且沒有考慮自動駕駛儀延遲對制導性能的影響。
對于同時考慮自動駕駛儀延時和攻擊角度約束的問題,文獻[7]基于線性化導引模型提出了一種新的非線性滑模導引律,但同樣只針對靜止或低速目標;文獻[8-9]基于反演動態面控制理論設計了攔截機動目標的IACG,但采用估計目標機動上界的辦法有失一般性,且估計值的準確與否直接影響制導性能;文獻[10]設計了攔截機動目標的積分滑模IACG,并采用高階滑模微分器估計目標加速度;文獻[11]同樣采用積分滑模設計IACG,不同之處在于其應用干擾觀測器估計目標加速度;文獻[12]引入擴張狀態觀測器估計目標機動擾動,并以此設計了非奇異終端滑模IACG。需要說明的是,上述文獻所采用的觀測器只能保證觀測誤差漸近收斂,而非有限時間收斂,且所有關于自動駕駛儀延時的IACG研究均未考慮視線角速率量測噪聲。
針對考慮自駕動態特性和視線角速率噪聲的機動目標攔截攻擊角度約束問題,本文利用線性滑模面結合非奇異終端滑模控制的方法設計了一種有限時間收斂IACG。為了抑制量測噪聲,設計一種跟蹤微分濾波器進行濾波;為了對目標機動干擾進行補償,采用誤差有限時間收斂的非齊次干擾觀測器對其精確估計。仿真結果表明,所設計導引律在噪聲抑制、干擾估計、制導精度和落角偏差方面都具有十分優異的性能。
1 制導模型描述
1.1 彈目相對運動方程
末制導過程的彈目相對運動是俯仰平面和偏航平面的耦合運動,本文為了研究方便,將其簡化為兩個通道的獨立運動,考慮到俯仰平面與偏航平面運動的相似性,因此本文只研究二維俯仰平面的彈目相對運動,如圖1所示,相對運動方程如下:
(1)
(2)
(3)
(4)
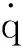
對式(2)求導可得
(5)
整理可得
(6)

(7)
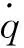
1.2 考慮自動駕駛儀動態特性含攻擊角度約束的制導模型
定義彈目遭遇時刻導彈速度矢量與目標速度矢量之間的夾角為攻擊角。設彈目遭遇時刻為tf,此時導彈和目標的彈道傾角分別為θMf、θTf,視線傾角為qf。基于零化視線角速率的思想,結合式(2)可得,在彈目遭遇時刻各傾角之間有以下關系成立:
VMsin(qf-θMf)=VTsin(qf-θTf)
(8)
期望攻擊角φd為定值按式(9)計算:
φd=θMf-θTf
(9)
考慮到在末制導過程中導引頭要鎖定目標,因此目標要始終處于導引頭的視場范圍內[13],而對導引頭視場角約束可通過對前置角的限制來處理,這里假定:
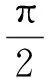
(10)
由式(8)~式(10)就可將彈目遭遇時刻期望攻擊角φd轉化為期望終端視線角qf來約束。
在導彈攻擊目標的制導過程中,導彈自動駕駛儀的動態特性是影響制導精度的一個主要因素[13]。為避免其造成制導精度下降,在建立含攻擊角度約束的制導模型時,將導彈自動駕駛儀近似為一階慣性環節,反映在時域里,即
(11)
式中τ為延遲常數;u為提供給導彈的垂直視線方向的加速度指令。
(12)
(13)
對式(12)求導,并將式(11)代入得
(14)
將式(13)代入式(14)整理得
(15)
(16)
2 考慮濾波的目標機動狀態估計
2.1 跟蹤微分濾波器設計
為得到純凈的制導信息,有必要對含有噪聲的視線角速率信號進行濾波處理。本節將利用跟蹤微分器的噪聲抑制能力,設計更加精確的跟蹤微分濾波器。
非線性跟蹤微分器的一般表達式為
(17)
式中v為帶噪聲的輸入信號;μ1為濾波之后的跟蹤信號;μ2為濾波之后的微分信號;γ為調節參數。
針對如下一階微分方程:
(18)
若式(18)有精確解y=y(x),且y(x)是n+1階連續可導,則y(x)可由泰勒公式展開為如下無窮級數:
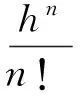
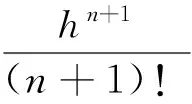
(19)
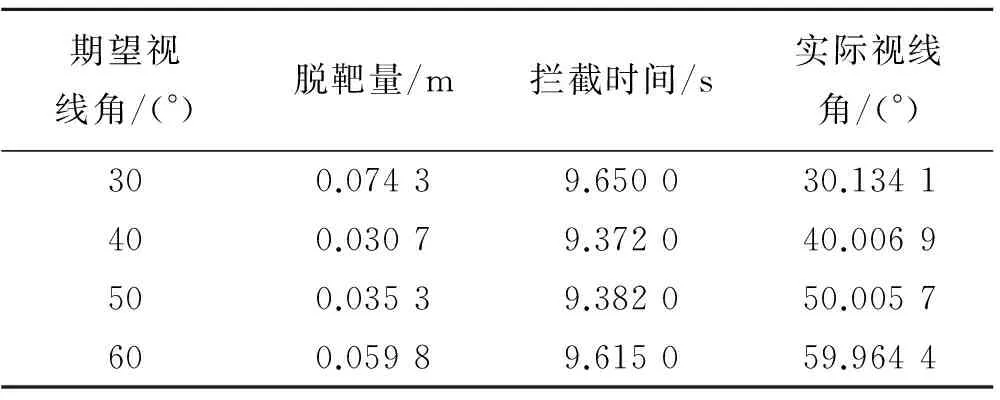
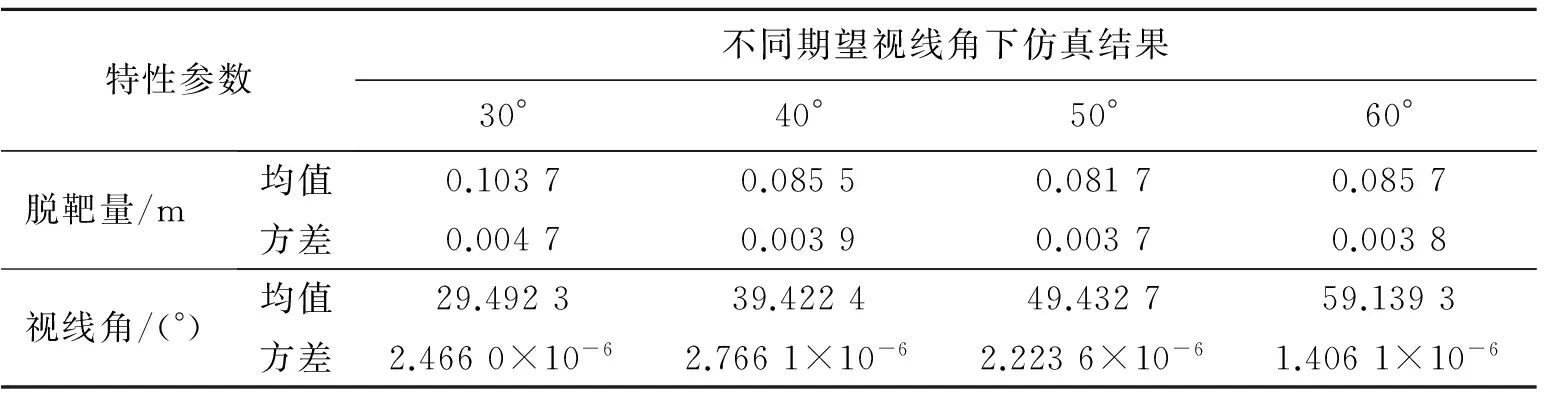
式中h為仿真步長,xk<ξ 如果令n=2,并且忽略高階無窮小項,可得式(18)的泰勒近似求解表達式,即 (20) 由式(20)得式(17)的輸出預測表達式為 (21) 將式(21)納入式(17),可得所設計的跟蹤微分濾波器表達式為 (22) 由于式(22)的第二式含有符號函數,在實際應用中可能會帶來系統抖振,影響濾波性能。而連續光滑的雙曲正切函tanh(x)取值無限趨近于±1,因此可采用雙曲正切函數tanh(s(x,t)/d)對符號函數進行連續化處理,其中邊界層厚度Δ=2πd[15]。 最終可得連續化后的跟蹤微分濾波器的表達式: (23) 2.2 基于狀態濾波的NHDO設計 為了對系統不確定性擾動進行跟蹤估計,文獻[14]基于非齊次微分器首次提出了可縮短暫態過程的非齊次干擾觀測器,它能在保證誤差有限時間收斂的同時提供最優的漸進精度。對于如下SISO非線性系統: (24) 式中u為系統控制輸入u∈R;g(t)為m-1次可導連續不確定函數,且gm-1(t)具有Lipschitz常數L。 則針對系統(24)可設計如下有限時間收斂非齊次干擾觀測器: (25) 其中,函數hi的表達式如下: 其中,λi>0,γi>0,i=0,1,2,…,m。 (27) 將2.1節所設計的跟蹤微分濾波器擴張到系統(27)中去,可得如下包含濾波的制導系統狀態方程: (28) 為了得到干擾f1*的Lipschitz常數,首先給出如下假設: 假設2[15]:系統(28)中時變彈目距離R滿足R≥Ro,Ro為導引頭盲區距離。在導引頭盲區內,導引頭不產生制導指令,導彈依靠慣性飛行。 結合假設1和假設2,干擾f1*的Lipschitz常數可由下式產生 (29) 式中VTmax、VMmax分別為目標和導彈的最大速度。 結合式(25)、式(26)可知,針對濾波后的制導系統(28),用于估計f1的非齊次干擾觀測器應設計為 (30) 根據文獻[16]的結論,系統經過有限時間的暫態過程之后,一定有下列等式成立: (31) 3.1 導引律設計 為了能使系統狀態在彈目交會前極短的時間內實現快速收斂,本節將利用線性滑模面和Terminal滑模控制相結合的辦法設計帶有攻擊角度約束的有限時間收斂制導律FSMG。 針對非線性制導系統(28),取so=αoμ3+μ4,為保證在有限時間達到滑模面so,設計一種具有遞歸結構的非奇異Terminal滑動模態為 (32) 其中,βo>0且1<ξ<2。 對式(32)求導可得: (33) 為確保滑動模態可達,選取如下快速冪次趨近律推導控制器: |s1|ηsgn(s1) (34) 其中,α1>0,α2>0,0<η<1。 由式(33)、式(34)可得制導指令: αoμ5-fo-f1)/b (35) 用觀測器(30)的輸出z1代替式(35)中的f1,并用2.1節所設計的跟蹤微分濾波器濾除視線角速率噪聲,得到最終可實現的有限時間收斂制導律為 βo-1ξ-1-αoμ5-fo-z1)/b (36) 3.2 收斂時間及穩定性分析 為證明導引律(35)作用下的制導系統有限時間收斂特性,首先給出如下Lyapunov有限時間穩定引理。 (37) 證明:將指令(35)代入式(33)有 αox3-fo-f1)=-α1s1-α2|s1|ηsgn(s1) (38) 取Lyapunov函數V=s12/2,對V求導并將式(38)代入得 |s1|η+1 其中,α1>0,α2>0,因為0<η<1,故0.5<(η+1)/2<1,滿足引理1條件,因此所設計的導引律是有限時間收斂的,且收斂時間上界滿足: (40) 同理可證在制導律(36)作用下的閉環導引系統也是有限時間收斂的。 Case1:不同期望視線角對比仿真 (1)不加視線角速率噪聲 仿真條件為:導彈速度大小VM=1000 m/s,初始彈道傾角θM=60°,初始位置(XM,YM)為(0,0);目標速度大小VT=680 m/s,初始航跡角θT=190°,初始位置(XT,YT)為(10 000,10 000),為驗證本文設計的攻擊角度約束制導律對機動目標的攔截能力,設目標以大小為5g的法向加速度正弦機動,即αT=50 sin(πt/3)m/s2。制導律參數設置為αo=1.5,α1=α2=10,βo=25,ξ=1.85,η=0.7;干擾觀測器參數設置為λo=8,λ1=5,λ2=3,γo=12,γ1=11,γ2=10,L=1.5;自動駕駛儀延時常數τ=0.5 s,制導指令周期取為10 ms,攔截彈過載限制為±30g。仿真如圖2~圖7和表1所示。 期望視線角/(°)脫靶量/m攔截時間/s實際視線角/(°)300.07439.650030.1341400.03079.372040.0069500.03539.382050.0057600.05989.615059.9644 分析圖4~圖6可知,針對不同的期望視線角,本文所設計的制導律都能保證滑模面在彈目交會前收斂于零,進而使視線角速率收斂到零,終端視線角達到期望角,證明了該制導律良好的有限時間收斂特性。而由表1數據可知,FSMG不僅落角偏差小,且脫靶量不超過0.1 m,滿足高精度制導要求,說明其在攔截機動目標時的有效性。 由圖7可看出,這種有效性是基于所設計的非齊次干擾觀測器對目標機動干擾的精確估計,雖然導彈初始段需用法向過載較大(圖3),但隨著干擾估計精度的提高和滑模面的收斂,導彈法向過載呈逐漸減小的趨勢,且在制導末段趨近于零,這樣導彈可在制導初始段充分利用其機動能力調整攻擊角度以及應對目標機動,制導末段則以較小的過載保證制導精度。 (2)加視線角速率噪聲 為了驗證2.1節設計的跟蹤微分濾波器的有效性,給視線角速率加0.01 rad/s的高斯白噪聲。設期望視線角為50°,跟蹤微分濾波器參數設置為γ=1.5,d=0.005,其余仿真條件同(1)。則一次濾波效果如圖8、圖9所示。 為進一步說明濾波器的有效性,在視線角速率加0.01 rad/s高斯白噪聲的情況下對30°、40°、50°、60°的期望視線角各做200次蒙特卡洛仿真,并計算脫靶量、視線角的均值和方差,結果如表2所示。 由圖8、圖9可看出,在保證視線角速率收斂的總體趨勢下,本文所設計的跟蹤微分濾波器能有效濾除干擾噪聲,使終端視線角更加接近期望角。另外由表2也可看出,針對不同的期望視線角,脫靶量均值幾乎不會超過0.1 m,視線角誤差不會超過1°,且方差均維持在零左右,進一步證明了跟蹤微分濾波器濾波的穩定性。 Case2:不同制導律對比仿真 為進一步說明本文設計的FSMG的優越性,將其與文獻[18]提出的基于反步法的考慮目標機動和自動駕駛儀動特性的終端角度約束滑模導引律BSMG進行50°角約束下仿真對比,仿真條件同(1),仿真結果如圖10~圖13所示。 表2 200次蒙特卡洛仿真視線角統計特性 由仿真結果可看出,整體而言,FSMG和BSMG都具有良好的有限時間收斂特性,能滿足機動目標攔截時的攻擊角度約束要求。但具體來看,FSMG視線角速率能收斂至零且始終維持于零,而BSMG的視線角速率最終收斂在0.2 (°)/s附近(圖12);在視線角的控制精度上,FSMG也比BSMG更加接近50°(圖13),這主要是因為FSMG滑模面的收斂精度要高于BSMG(圖11),在收斂速度方面,FSMG也要快于BSMG,盡管FSMG的法向過載稍大于BSMG,但始終在導彈可用過載范圍內。而基于反步法設計的BSMG制導律不僅形式復雜,且易造成虛擬控制項的微分膨脹問題,相比之下,FSMG制導律形式簡單,更適合工程應用。 本文采用線性滑模面和終端滑模控制理論設計了一種考慮自動駕駛儀動態特性的有限時間收斂攻擊角度約束導引律。為濾除視線角速率噪聲,設計了一種跟蹤微分濾波器,建立了包含濾波的導引方程;針對目標機動帶來的不確定性擾動,設計非齊次干擾觀測器對其進行精確估計,并在制導律中加以補償,仿真結果表明: (1)所設計的跟蹤微分濾波器具有良好的濾波特性,能有效克服視線角速率噪聲對制導精度的不利影響; (2)采用非齊次干擾觀測器能夠在有限時間內對目標擾動快速跟蹤估計; (3)采用線性滑模面和終端滑模相結合的方法設計的有限時間收斂導引律能夠滿足攻擊角度約束要求,克服導彈動態延遲影響,且導引律形式簡單,易于工程實踐。 [1] 蔡洪,胡正東,曹淵.具有終端角度約束的導引律綜述[J].宇航學報,2010,31(2):315-323. [2] Erer K S,Merttop?uoɡlu O. Indirect impact-angle-control against stationary targets using biased pure proportional navigation[J].Journal of Guidance,Control, and Navigation,2012,35(2):700-703. [3] Erer K S,?zg?ren M K. Control of impact angle using biased proportional navigation[C]//AIAA Guidance,Navigation,and Control(GNC) Conference,2013:1-15. [4] Ratnoo A,Ghose D. Impact angle constrained interception of stationary targets[J].Journal of Guidance,Control, and Navigation,2008,31(6):1816-1821. [5] Ratnoo A,Ghose D. Impact angle constrained guidance against nonstationary nonmaneuvering targets[J].Journal of Guidance,Control, and Navigation,2010,33(1):269-275. [6] Zhang Y A,Ma G X,Wu H L. A biased proportional navigation guidance law with large impact angle constraint and the time-to-go estimation[J].Proceedings of the Institution of Mechanical Engineers,Part G: Journal of Aerospace Engineering,2014,228(10):1725-1734. [7] Lee C H,Kim T H,Tahk M J. Design of impact angle control guidance laws via high -performance sliding mode control[J].Proceedings of the Institution of Mechanical Engineers,Part G: Journal of Aerospace Engineering,2012,227(2):235-253. [8] 曲萍萍,周荻.考慮導彈自動駕駛儀二階動態特性的導引律[J].系統工程與電子技術,2011,33(10):2263-2267. [9] 張堯,郭杰,唐勝景,等.機動目標攔截含攻擊角約束的新型滑模制導律[J].兵工學報,2015,36(8):1143-1157. [10] Zhang Z,Li S,Luo S. Terminal guidance laws of missile based on ISMC and NDOB with impact angle constraint[J].Aerospace Science and Technology,2013,31(1):30-41. [11] Zhang Z X,Li S H,Luo S. Composite guidance laws based on sliding mode control with impact angle constraint and autopilot lag[J].Transactions of the Institute of Measurement and Control,2013,35(6):764-776. [12] Xiong S,Wang W,Liu X,et al. Guidance law against maneuvering targets with intercept angle constraint[J].ISA Transactions,2014,53(4):1332-1342. [13] 周慧波.基于有限時間和滑模理論的導引律及多導彈協同制導研究[D].哈爾濱:哈爾濱工業大學,2015. [14] Shtessel Y B,Shkolnikov I A,Levant A. Smooth second-order sliding modes: missile guidance application[J].Automatic,2007,43(8):1470-1476. [15] 馬克茂,賀風華,姚郁.目標機動加速度的估計與導引律實現[J].宇航學報,2009,30(6):2213-2219. [16] Levant A. Non-homogeneous finite-time-convergent differentiator [C]//Preceedings of Decision and Control,2009 held jointly with the 2009 28th Chinese Control Conference. CDC/CCC 2009.Proceedings of the 48th IEEE Conference on. IEEE,2009:8399-8404. [17] Yu S H,Yu X H,Shirinzadeh B,et al. Continuous finite-time control for robotic manipulators with terminal sliding mode[J].Automatica,2005,41(11):1957-1964. [18] 孫勝,張華明,周荻.考慮自動駕駛儀動態特性的終端角度約束滑模導引律[J].宇航學報,2013,34(1):69-78. (編輯:呂耀輝) NHDO-based impact angle control guidance law for maneuvering target WANG Bin, LEI Hu-min, LI Jiong, SHAO Lei, YE Ji-kun (Air and Missile Defense College, Air Force Engineering University, Xi'an 710051, China) In order to control the missile to attack the maneuvering target with desired terminal impact angle precisely in finite time, finite time convergence guidance law based on terminal sliding mode control theory is proposed according to simplified autopilot lag by the first order inertial element. To filter the noise of the LOS rate, a nonlinear tracking differential filter is proposed and the state equation of the guidance system is constructed considering filtering. Meanwhile, a non-homogeneous disturbance observer is devised based on the equation of state proposed to track and estimate the target maneuver disturbance. Simulation results show that the proposed guidance law can achieve the aim of filtering the LOS rate noise, precisely tracking the maneuver state of the targets, eliminating the adverse effect caused by the dynamic delay, satisfying the requirements of terminal impact angle and guidance precision. lmpact angle constraint;finite time convergence;tracking differential filter;non-homogeneous disturbance observer;guidance law 2016-11-25; 2017-01-10。 國家自然科學基金(61573374;61503408);航空科學基金(20150196006)。 王斌(1993—),男,碩士生,研究方向為飛行器制導與控制。E-mail:wwbb125100@qq.com V448 A 1006-2793(2017)04-0517-08 10.7673/j.issn.1006-2793.2017.04.021
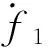
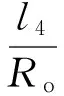
3 有限時間收斂導引律
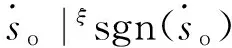
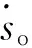

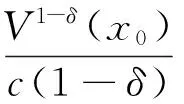
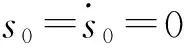
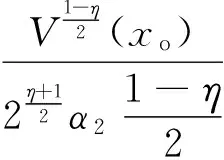
4 仿真實例與分析
5 結論

