Rossini 型氣體熱量計非穩態溫度場的優化分析

杜軍燕，王玉剛，潘江，張洪軍

（中國計量大學計量測試工程學院，浙江杭州310018）

Rossini 型氣體熱量計非穩態溫度場的優化分析

杜軍燕，王玉剛，潘江，張洪軍

（中國計量大學計量測試工程學院，浙江杭州310018）

為優化Rossini型氣體熱量計溫度場均勻性以減小測量不確定度，采用多重參考系法（MRF）和標準k-ε湍流模型對Rossini型氣體熱量計的溫度場進行三維瞬態數值模擬，分別得到攪拌器轉速、燃燒室高度對量熱容器內非穩態溫度場的影響，特別是對燃燒室與吸熱介質之間熱傳遞的影響以及對吸熱介質溫度均勻性的影響，同時確定溫度傳感器的最佳安裝位置。結果表明：攪拌器槳葉最佳轉速為420r/min，這時燃燒室壁面與吸熱介質之間的傳熱效率最大，并且吸熱介質內監測點溫度的標準偏差保持在1.5mK以內。燃燒室高度減小可以提高吸熱介質的溫度均勻性，加熱階段中，燃燒室高度從180mm降低到140mm時，監測點溫度的標準偏差從26mK降低到7.5mK。溫度傳感器的最佳安裝位置在燃燒室對稱軸及導流筒對稱軸的等距線上離殼體底部25mm處。

Rossini型氣體熱量計；標準k-ε湍流模型；非穩態溫度場；數值模擬

0 引言

Rossini型氣體熱量計用于測定純氣體、天然氣的熱值，是具有最高準確度等級的氣體熱值測定裝置，可直接測定氣體熱值并實現熱值結果溯源到國際單位[1-2]。Rossini型氣體熱量計測量試驗包括電校正過程及燃燒過程，電校正過程以電加熱功率替代氣體燃燒的熱功率，用于準確測量氣體熱量計的當量比熱，提高最終測量結果的準確度。自Rossini[3]建立測量純甲烷熱值的Rossini型熱量計以來，國外相關學者一直致力于提高Rossini型氣體熱量計測量結果的不確定度。

Pittam等[4]在Rossini熱量計的基礎上，建立了純氣體熱值測量裝置，并且測定純氣體熱值數據與Rossini的數據偏差小于0.017%。Dale等[5]改進了氣體樣品質量的稱量方法，提高了燃燒氣體質量測量的不確定度。Jaeschke等[6]指出熱值的不確定度主要來自于質量測量和溫度測量，并研制出一套不確定度約為0.01%的自動稱重與校準裝置。Haloua等[7]研制出周邊等溫型基準氣體熱量計，詳細介紹了該熱量計的建立及其相應測試單元的優化方法。后續對熱量計的三維模型進行數值計算分析指出只有90%的發熱量被吸熱介質吸收，剩下10%的熱量被熱量計容器吸收[8]。Schley等[9]研制了一種基準氣體熱量計，并由德國物理技術研究院組裝測試，該熱量計測量甲烷熱值的不確定度〈0.05%。法國國家實驗室第一次公開研究多年的周邊等溫型基準氣體熱量計的測定數據及詳盡的不確定度分析[10]，數據表明測量甲烷純度為99.9995%的熱值為55509.996kJ/kg，并且擴展相對不確定度為0.091%（k=2）。國內對熱量計的研究起步較晚，胡日恒等[11]建立國內第一套精密氧彈熱量計。中國計量科學研究院的水流式熱量計測定純甲烷熱值的相對不確定度達到1.0%（k=2）[12]。中國科學院復建了氧彈熱量計，測定純甲烷熱值的相對不確定度可達0.6%[13]。中國石油西南油田分公司天然氣研究院采用燃燒法，建立了一套熱值相對不確定度優于0.25%的1級發熱量直接測定裝置[14]。呂丹妮等[15]對Rossini型氣體熱量計開發中的幾項關鍵技術進行了論述。

文獻研究表明優化吸熱介質的溫度均勻性、強化燃燒室與吸熱介質之間的換熱具有十分重要的意義[8]。國內外相關學者著重對熱量計的研制與測試研究，基于數值模擬方法進行的機理研究不多。基于以上背景，本文使用Fluent軟件，利用標準k-ε湍流模型對Rossini型氣體熱量計電校正過程中量熱容器的溫度場進行了三維瞬態數值模擬，分析了攪拌器轉速、燃燒室高度對量熱容器內的非穩態溫度場的影響，特別是對燃燒室與吸熱介質之間熱傳遞的影響以及對吸熱介質溫度均勻性的影響，同時確定了Rossini型氣體熱量計的量熱容器內溫度傳感器的最佳安裝位置，對優化Rossini型氣體熱量計裝置設計、提高測量結果的不確定度有所指導。

1 物理模型建立

Rossini型氣體熱量計的量熱容器的結構如圖1所示。本文模擬的物理模型經過簡化，如圖2所示。量熱容器的殼體是不規則桶體，其高度為270mm。燃燒室簡化成如圖2所示的圓柱體，其直徑為50mm，高度為100 mm，其表面設為電加熱面。導流筒的直徑為50 mm，高度為170 mm，攪拌器槳葉直徑為40 mm，攪拌器的安裝高度為135 mm。

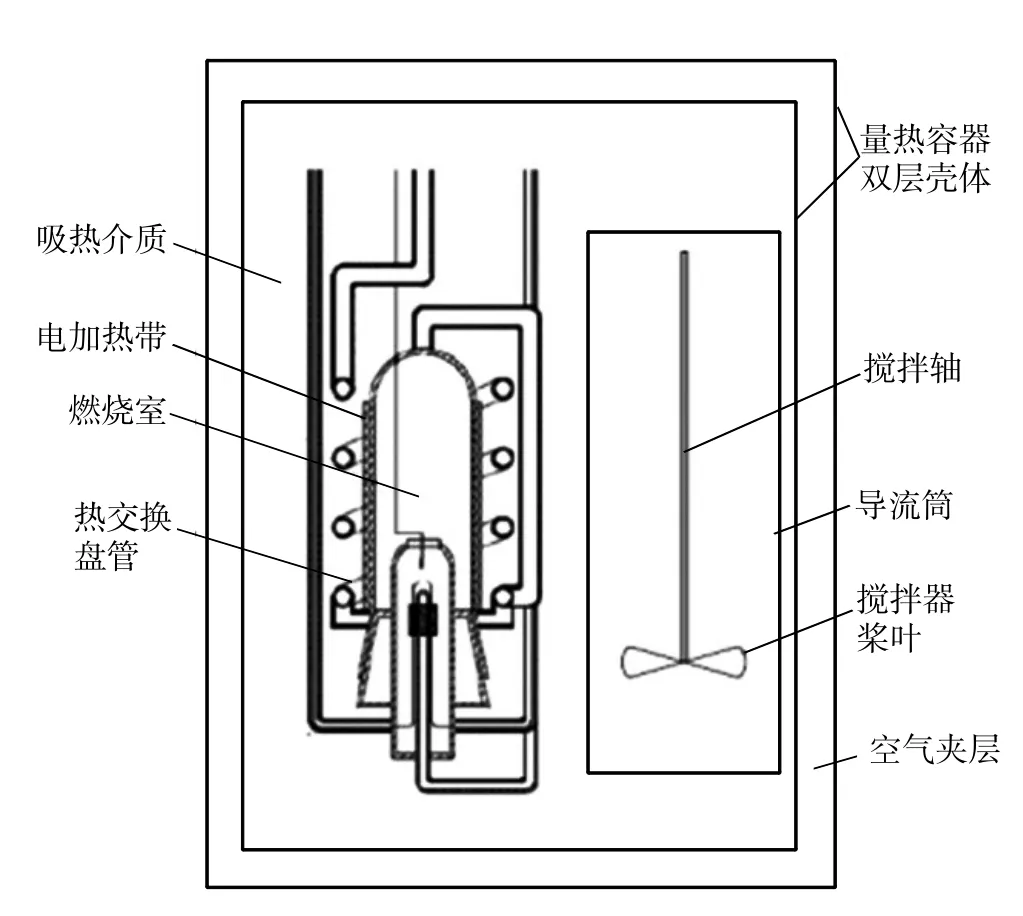
圖1 Rossini型氣體熱量計量熱容器的結構示意圖

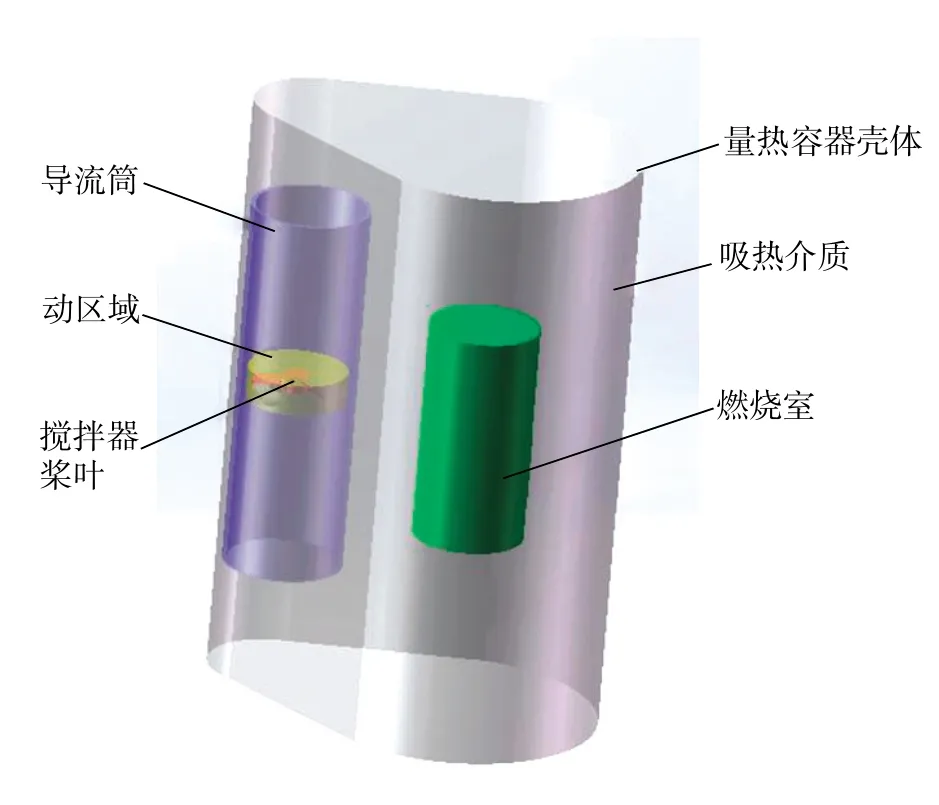
圖2 Rossini型氣體熱量計量熱容器的物理模型

2 數學模型及參數設置

2.1 數學模型

在直角坐標系中，根據有限體積法思想，引入通用輸送方程，將φ取為不同的變量，把擴散系數Γ和源項Sφ取為適當的表達式，則連續性方程、動量方程、能量方程、紊動能方程、紊動耗散方程都可寫成統一的形式，即：

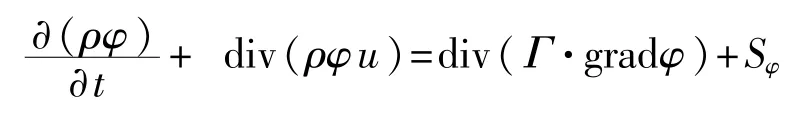
2.2 參數設置

量熱容器內吸熱介質采用純水，假設流體為不可壓縮常物性（25℃下），其密度為998.2kg/m3，粘度為0.001003Pa·s，比熱容為4182kJ/（kg·K）。

量熱容器殼體的所有表面及導流筒的側表面設為無滑移、絕熱壁面邊界條件，攪拌器槳葉表面設為旋轉運動壁面邊界條件，導流筒的上下界面設為內部界面，量熱容器殼體、導流筒、攪拌器槳葉的材料均設置為不銹鋼304L，與實物一致。加熱階段時，燃燒室的表面設為等熱流密度壁面邊界條件，熱流密度為3107W/m2；加熱前階段與加熱后階段時，燃燒室的表面設為絕熱。燃燒室的材料設置為高硼玻璃。

量熱容器內吸熱介質的初始溫度為23.5℃，量熱容器殼體的初始溫度為25℃，量熱容器外部環境溫度為25℃。

3 計算

采用ANSYS/ICEM軟件進行非結構化網格劃分，在攪拌器的附近進行網格加密，網格數量為282萬個。本文模擬首先對網格數量的無關性進行了驗證。

計算軟件使用商業軟件Fluent 6.3，采用三維瞬態湍流模型。采用多重參考系法（MRF）解決靜止部分流體與轉動的攪拌器之間的相對運動問題，整個流體區域分成兩部分，攪拌器及其附近的流體區域設置為旋轉坐標系，其他流體區域設置為靜止坐標系。通過定義交界面完成兩個區域的動量、能量交換。

計算采用標準k-ε湍流模型，其參數為σu=0.09，σk=1，σε=1.3，σ1=1.44，σ2=1.92，其中，σu、σ1、σ2為模型常數，σk、σε分別為k和ε的湍流普朗特數。

壓力與速度的耦合計算采用標準的SIMPLE算法，對流項的離散采用二階迎風格式。方程的收斂殘差條件：連續性方程為1×104，動量方程為1×104，能量方程為1×106。

4 計算結果與分析

4.1 攪拌器槳葉轉速對溫度場的影響

研究攪拌器槳葉不同轉速對量熱容器內吸熱介質溫度場的影響時，其他條件保持一致，以加熱階段和加熱后階段為例，其中0～1500s為加熱階段，1501～2700s為加熱后階段。如圖3所示，討論了攪拌器槳葉轉速分別為120，240，360，480，600 r/min時，吸熱介質平均溫度隨時間的變化。

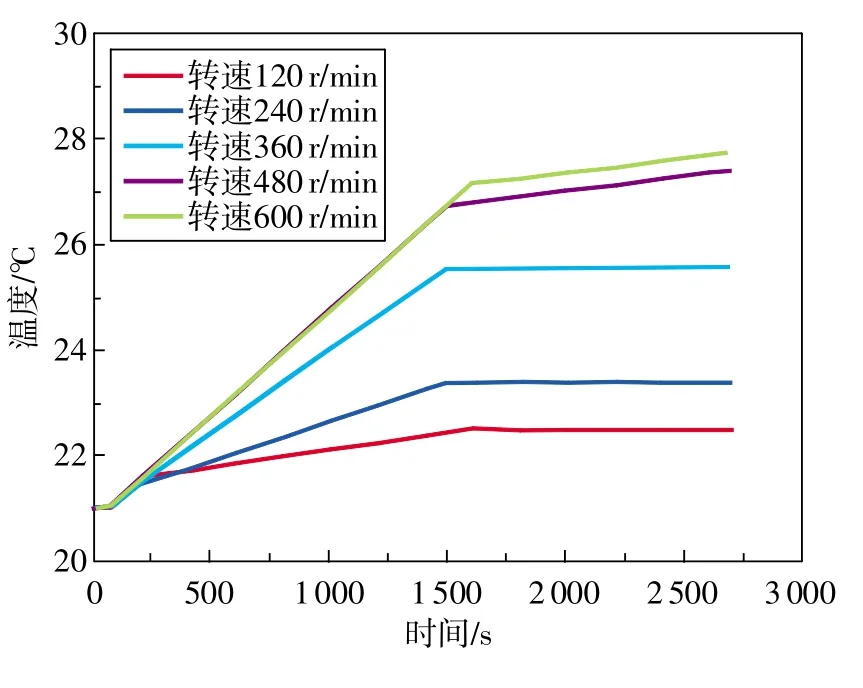
圖3 不同轉速下，吸熱介質平均溫度隨時間的變化

4.1.1 攪拌器槳葉轉速對傳熱效率的影響

如圖3所示，加熱階段中，燃燒室表面的熱流密度相同條件下，吸熱介質平均溫度隨時間變化曲線的斜率隨著轉速的增大而增加，這主要是由于轉速增大后引起吸熱介質內湍流強度的增加，從而導致吸熱介質與燃燒室之間的對流傳熱得到強化，使燃燒室的熱量更多地傳遞到吸熱介質中，吸熱介質平均溫度的溫升增大。

計算攪拌器槳葉轉速從120～600 r/min，以差值120r/min遞增，在某一段時間內，任意兩條相鄰的溫度隨時間變化曲線之間的面積代表該段時間內吸熱水浴因轉速增大120r/min而增加的吸熱量。增大相同轉速的情況下，隨著轉速增大，吸熱介質吸熱量的增量呈現先增大后減小的趨勢，因此，燃燒室與吸熱介質之間傳熱隨著轉速的增大而有所增強，但是增加的強度先變大后變小。只有轉速在240～480 r/min范圍內，增大轉速對提高吸熱介質內的傳熱效率有明顯幫助。

在加熱后階段中，熱量輸入停止，攪拌繼續工作。當轉速處于120～360r/min區間內，加熱后階段吸熱介質的平均溫度保持恒定不變，而轉速在480 r/min及以上區間，加熱后階段的吸熱介質的平均溫度呈緩慢升高的趨勢。這是由于攪拌器槳葉的動能轉化為熱能而引入的熱量輸入，并且熱量輸入隨著轉速增大而增大，直至引起吸熱介質溫度有明顯溫升。攪拌器轉速增大，那么因攪拌引起的吸熱介質溫升也增大，也就導致熱值測量結果中溫升測量引入的誤差增大。

假設電加熱量（或燃燒熱）被吸熱介質完全吸收，不考慮量熱容器殼體等自身吸熱對應吸熱介質的理論溫升為5℃。根據文獻[8]的研究結果，燃燒室的加熱量中實際最多只有90%的熱量能被吸熱介質吸收，對應吸熱介質的溫升為4.5℃。不同攪拌器槳葉轉速下，吸熱介質平均溫度的溫升如表1所示。吸熱介質平均溫度的溫升隨著攪拌器槳葉轉速的增大而增大，甚至超過最理想狀態的5℃，這是由于槳葉的動能轉化為熱能引入的能量輸入。

表1 不同轉速下吸熱介質平均溫度的溫升

4.1.2 攪拌器槳葉轉速對溫度均勻性的影響

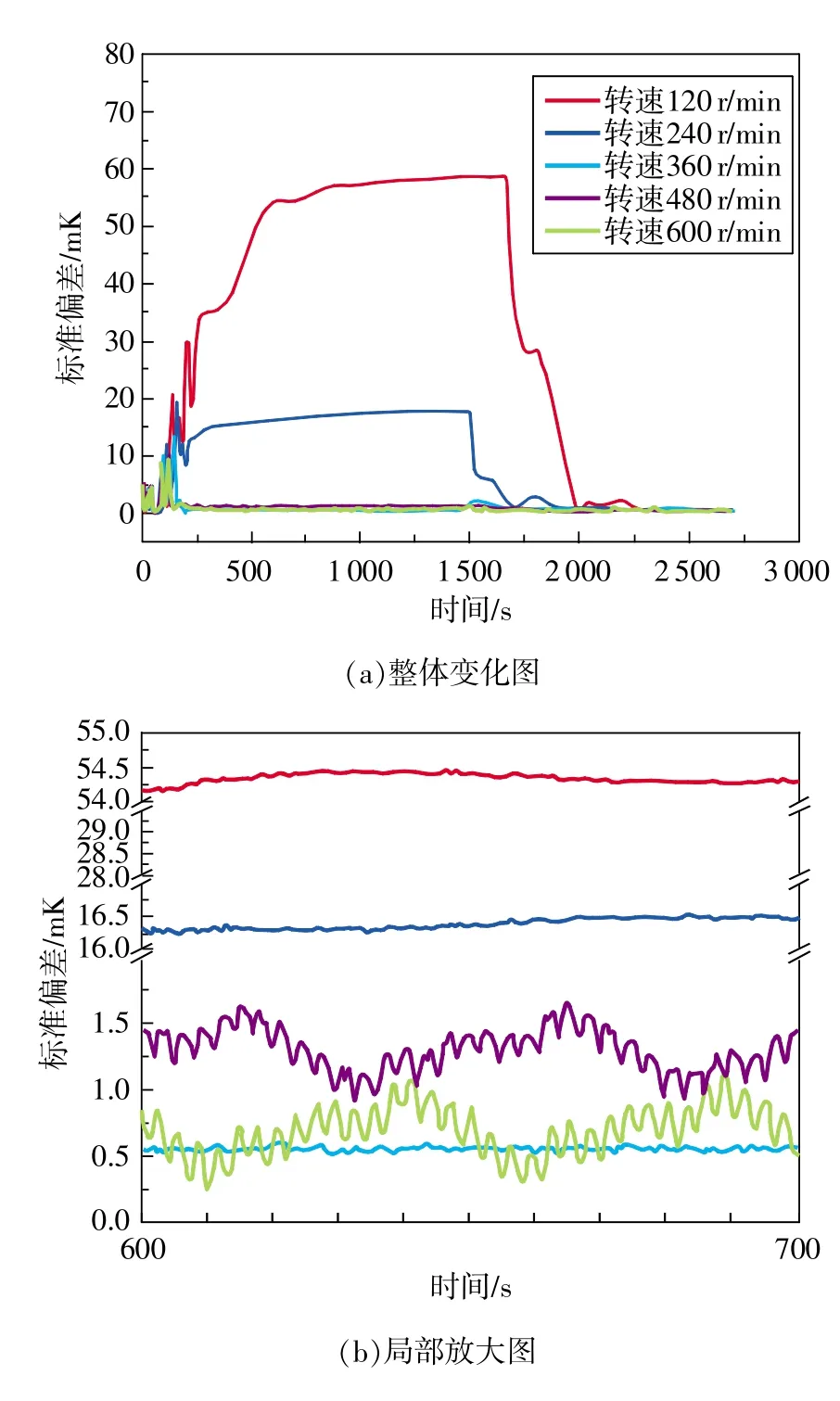
圖4 不同轉速下，吸熱介質溫度不均勻性的標準偏差隨時間的變化

參考恒溫槽溫度均勻性測試的溫度點測試位置的選取，取量熱容器中吸熱介質的8個位置作為監測點，分析不同攪拌器槳葉轉速下，監測點溫度的標準偏差隨時間變化的情況，即代表量熱容器中吸熱介質的溫度均勻性隨時間變化，如圖4所示。攪拌器槳葉轉速在240r/min及以下時，從0s起，監測點溫度的標準偏差從0開始，隨著攪拌和熱量輸入引起的擾動增加，監測點溫度的標準偏差開始迅速增大。500s以后，吸熱介質循環流動穩定，監測點溫度的標準偏差隨著熱擾動的存在而緩慢增大。1501s以后，沒有熱量輸入，攪拌器繼續工作，監測點溫度的標準偏差急劇減小后維持在2mK以內。攪拌器槳葉轉速在360r/min及以上時，監測點溫度的標準偏差在加熱階段和加熱后階段一直維持在2mK以內。這是由于在攪拌器轉速大的條件下吸熱介質能夠迅速形成良好的循環流動。加熱階段下，監測點溫度的標準偏差隨著轉速的增大而減小，轉速從120 r/min逐漸增大到360r/min時，監測點溫度的標準偏差從55 mK減小到0.5 mK，轉速從360 r/min逐漸增大到540 r/min時，監測點溫度的標準偏差始終保持在1.5mK以內。轉速小于360r/min時，增大轉速可以有效改善吸熱介質的溫度不均勻性，超過這個范圍，增大轉速對溫度均勻性的提高并不顯著。

綜合傳熱效率和溫度均勻性的影響，本文選取360r/min和480 r/min的平均值420 r/min作為攪拌器的最佳轉速。此時，燃燒室與吸熱介質之間的傳熱效果最好，同時監測點溫度的標準偏差在1.5 mK以內。

4.2 燃燒室高度對溫度場的影響

討論燃燒室不同高度對量熱容器內吸熱介質溫度場的影響時，取攪拌器槳葉的轉速為420r/min，分析完整測量過程中吸熱介質溫度不均勻性的變化情況。其中0～1200s為加熱前階段，1201～2400s為加熱階段，2401～3600s為加熱后階段。如圖5所示，討論了燃燒室高度分別為140，160，180mm時，吸熱介質溫度不均勻性的標準偏差隨時間的變化情況。

圖5 不同燃燒室高度下，吸熱介質溫度不均勻性的標準偏差隨時間的變化

從圖中可知，加熱前階段和加熱后階段因熱擾動小，監測點溫度的標準偏差維持在2 mK以內，并且隨著燃燒器高度的減小而減小。加熱階段由于熱擾動最大，吸熱介質的溫度均勻性弱于其他兩個階段，燃燒室高度為140mm時，監測點溫度的標準偏差為7.5mK，并隨著燃燒室高度的增大而增大。這是由于燃燒室高度增加，量熱容器殼體高度不變的情況下，吸熱介質的循環通道面積減小，從而吸熱介質的循環流動受到限制而導致傳熱受到削弱。雖然吸熱介質與燃燒室的傳熱面積隨燃燒器高度增大而增大，對增強傳熱有利，但是仍不能抵消吸熱介質循環流動減弱引起的傳熱減弱。燃燒室與吸熱介質換熱面積得到保證的情況下，減小燃燒室高度有利于增強吸熱介質的溫度均勻性，特別是加熱階段。

4.3 溫度傳感器最佳安裝位置

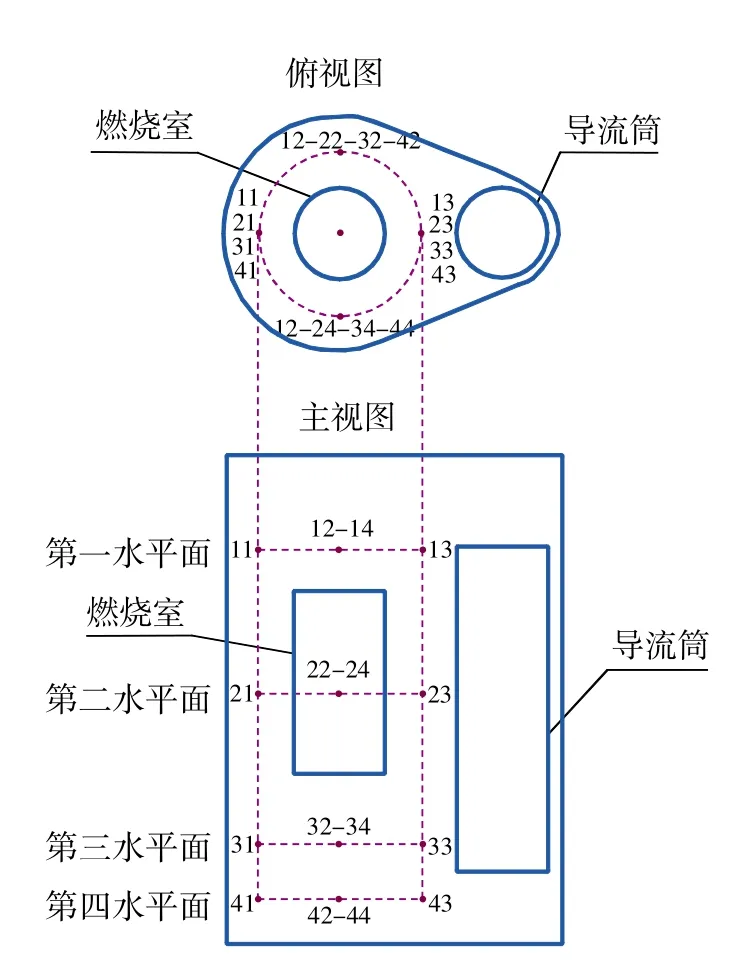
圖6 監測點分布圖

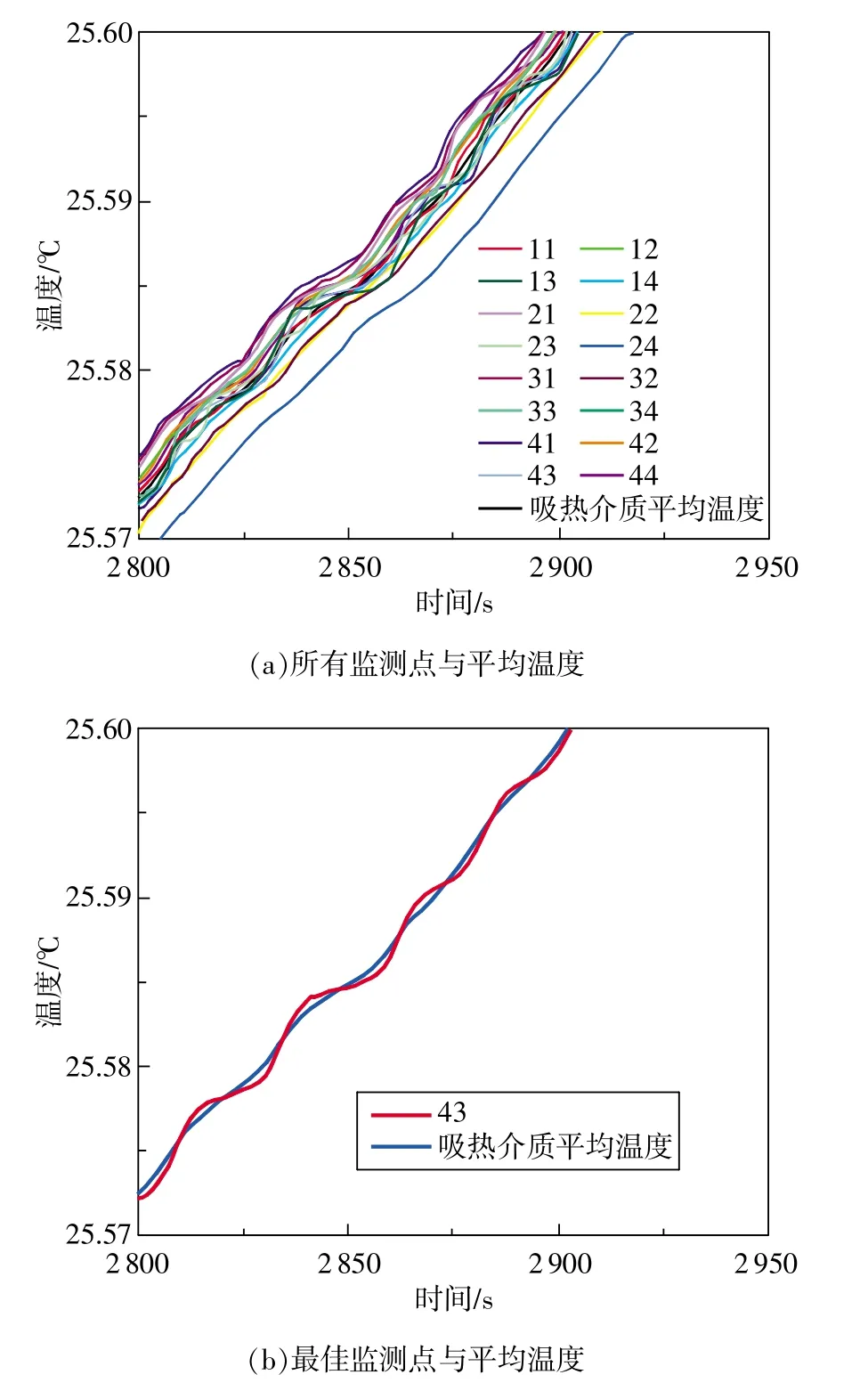
圖7 不同監測點溫度隨時間變化

為了確定最能代表吸熱介質平均溫度的溫度測量點，即溫度傳感器最佳安裝位置。在吸熱介質中布置監測點，通過分析監測點溫度及吸熱介質平均溫度隨時間變化的情況來確定最佳溫度測量點。監測點分布在燃燒室的周圍，如圖6所示，其中11～14位于第一水平面，21～24位于第二水平面，31～34位于第三水平面，41～43位于第四水平面。以加熱后階段中100s內吸熱介質平均溫度與監測點溫度變化曲線為例，如圖7所示，監測點43處溫度與介質平均溫度的偏差最小，因此其相比其他監測點更能代表吸熱介質平均溫度，可視為溫度傳感器最佳安裝位置，監測點43對應的具體位置為燃燒室對稱軸及導流筒對稱軸的等距線上離殼體底部25mm處。

5 結束語

本文采用數值模擬的方法研究了Rossini型氣體熱量計溫度場的特性，為設計更高不確定度水平的熱量計提供仿真數據指導。模擬攪拌器槳葉在不同轉速、燃燒室在不同高度時，Rossini型氣體熱量計的量熱容器內非穩態溫度場變化，獲得以下結論：

1）攪拌器槳葉的最佳轉速為420r/min。這是由于只有在240～480 r/min范圍內增大轉速可顯著強化吸熱介質的傳熱效率。轉速低于360r/min時，增大轉速可以有效改善吸熱介質的溫度不均勻性，監測點溫度的標準偏差在轉速為360 r/min時達到最小值0.5mK，超過這個轉速范圍，增大轉速不能提高吸熱介質的溫度均勻性，并且會增加攪拌引入的熱量從而增大溫度測量的誤差。

2）燃燒室高度減小可以提高吸熱介質的溫度均勻性，特別是在加熱階段。加熱階段中，燃燒室高度從180mm降低到140mm時，監測點溫度的標準偏差從26mK降低到7.5mK。這主要是吸熱介質的循環流動受阻引起吸熱介質內的傳熱效率降低和溫度均勻性變差。

3）最能代表吸熱介質平均溫度的位置在燃燒室對稱軸及導流筒對稱軸的等距線上離殼體底部25mm處，該結論可為溫度傳感器測量點的布置提供參考依據。

本文研究基于純數值模擬研究，可為后續熱量計的結構優化和改進提供依據，但是建立一套國內領先水平的Rossini型氣體熱量計還需要進行相應的實驗驗證，后續工作需要通過實驗與數值模擬有機結合來不斷實現熱量計的優化，研制出不確定度優于0.3%的Rossini型氣體熱量計。

[1]JAESCHKE M，SCHMüCKER A，PRAMANN A，et al.GERG Project：Development and setup of a new combustion reference calorimeter for natural gases[J].International Journal of Thermophysics，2007，28（1）：220-244.

[2]VILLERMAUX C，ZARéA M，HALOUA F，et al.Measurements of gas calorific value:a new frontier to be reached with an optimised reference gas calorimeter[C]∥23rdworld gas conference.Amsterdam：International gas Union，2006.

[3]ROSSINIFD.The heat of formation of water[J].Proceedings of the National Academy of Sciences，1930，16（11）：694-699.

[4]PITTAM D A，PILCHER G.Measurements of heats of combustion by flame calorimetry.part 8.-Methane ethane propane n-butane and 2-methylpropane[J].Journal of the Chemical Society，Faraday Transaction 1：Physical Chemistry in Condensed Phases，1972（68）：2224-2229.

[5]DALE A，LYTHALL C，AUCOTT J，et al.High precision calorimetry to determine the enthalpy of combustion of methane[J].Thermochimica Acta，2002，382（1）：47-54.

[6]JAESCHKE M，BENITO S A，CREMONESI P L，et al.GERG Project：Development and set-up of a new reference calorimeter[J].Gartenbauwissens-Chaft，2004，54（4）：179-184.

[7]HALOUA F，HAY B，FILTZ J R.New french reference calorimeter for gas calorific value measurements[J].Journal of Thermal Analysis and Calorimetry，2009，97（2）：673-678.

[8]HALOUA F，PONSARD J N，LARTIGUE G，et al.Thermal behaviour modelling of a reference calorimeter for natural gas[J].International Journal of Thermal Sciences，2012，55（3）：40-47.

[9]SCHLEY P，BECK M，UHRIG M，et al.Measurements of the calorific value of methane with the new GERG reference calorimeter[J].International Journal of Thermophysics，2010，31（4）：665-679.

[10]HALOUA F，FOULON E，ALLARD A，et al.Traceable measurementanduncertaintyanalysisofthegross calorific value of methane determined by isoperibolic calorimetry[J].Metrologia，2015，52（6）：741-755.

[11]胡日恒，安緒武，談夫.精密氧彈量熱計及苯甲酸燃燒熱的測定[J].化學學報，1981（增刊1）：18-26.

[12]蘇毅，駱科東.我國天然氣流量計量技術現狀及發展趨勢分析[J].石油儀器，2015（5）：8-12.

[13]王海峰，李佳，孫國華，等.基準氣體熱量計研究進展[J].石油與天然氣化工，2014（2）：196-199.

[14]李克，潘春鋒，張宇，等.天然氣發熱量直接測量及賦值技術[J].石油與天然氣化工，2013，42（3）：297-301.

[15]呂丹妮，張洪軍，韓偉棟.Rossini型氣體熱值測量裝置中的幾個關鍵技術[J].儀器儀表學報，2014，35（12）：151-154.

（編輯：李妮）

Numerical simulation of unsteady temperature field in Rossini gas calorimeter

DU Junyan，WANG Yugang，PAN Jiang，ZHANG Hongjun
（College of Metrology and Measurement，China Jiliang University，Hangzhou 310018，China）

In order to optimize the temperature field uniformity of Rossini gas calorimeter to minimize the measurement uncertainty，3D transient numerical simulation was carried out for temperature field of Rossini gas calorimeter based on MRF model and standard k-ε turbulence model，and the influence of rotational speed and the combustion chamber height on unsteady temperature field in calorimeter vessel was also obtained，especially the influence on heat transfer between combustion chamber and heat transfer medium.Meanwhile，the best installation location of temperature sensor was also determined.The results indicate that rotational speed of 420 r/min can be regarded as the optimal rotational speed of stirrer paddle，the heat transfer between combustion chamber wall surface and heat transfer medium is maximum at this time，the standard deviation of the temperature at the monitoring point of heat transfer medium is within 1.5 mK.Reduction of the height of the combustion chamber can improve the temperature homogeneity of the heat transfer medium.At the heating stage，the standard deviation of temperature at the monitoring points is reduced from 26mK to 7.5mK when the combustion chamber height is reduced from 180mmto 140mm.The optimum installation position of the temperature sensor is 25mm to the bottom of shell，on the equidistant line of the symmetry axis of combustion chamber and guide cylinder.

Rossini gas calorimeter；standard k-ε turbulence model；unsteady temperature field；numerical simulation

A

1674-5124（2017）08-0119-06

2016-11-05；

2017-01-13

國家質檢公益性行業科研專項項目（201410133）

杜軍燕（1992-），女，江西吉安市人，碩士研究生，專業方向為能源計量。

王玉剛（1972-），男，河北寧晉縣人，副教授，博士，主要從事能源計量研究。

10.11857/j.issn.1674-5124.2017.08.024