定量光聲層析成像的研究進展

孫 正,鄭 蘭

定量光聲層析成像的研究進展

孫 正*,鄭 蘭

(華北電力大學 電子與通信工程系，河北 保定 071003)

光聲層析(Photoacoustic tomography,PAT)成像結合了超聲成像的高分辨率和光學成像的高對比度的優勢，是一種新型的生物醫學成像模式。PAT成像算法包含兩個逆問題，即根據組織產生的光聲信號構建初始聲壓分布圖(即圖像重建)以及在此基礎上估算成像區域的光學特性參數。后者是一個非線性的不適定問題，通常稱為定量光聲層析(Quantitative photo-acoustic tomography，qPAT)成像。本文在介紹光聲成像原理的基礎上，對主要的qPAT算法進行綜述，討論各自的優勢和不足，并對未來可能的發展方向進行展望。

定量光聲成像； 圖像重建； 逆問題； 光吸收系數； 散射系數； Gruneisen系數

1 引 言

光聲層析(Photoacoustic tomography,PAT)成像是近年來發展起來的一種非電離式的新型生物醫學成像方法。它采用脈沖激光對生物組織進行激發，獲取組織的光吸收系數分布情況，因此繼承了光學成像的一系列優點，如對組織損傷小、對比度高、可進行功能成像和分子成像等[1]。PAT探測的是組織產生的超聲波信號，因此它繼承了超聲成像對深層組織成像的高分辨率的特點[2]。與X射線成像、超聲成像和磁共振成像等傳統的醫學成像技術相比，PAT技術的優勢主要體現在：采用非電離波段，成像過程中不改變生物組織的屬性；較容易界定組織產生的光聲信號和組織的生理狀態之間的關系；可與超聲或光學成像技術相結合，以獲得更多的診療信息；可根據實際應用的需要調整成像深度和成像分辨率等[3]。

目前，對生物PAT成像系統的改進主要體現在三個方面：第一，探測組織產生的光聲信號的方法，除了采用傳統的基于壓電效應的超聲換能器或者PVDF 膜的水聽器之外，還可利用光學方法實現光聲信號的探測。例如：探測光聲效應引起的組織折射率的變化[4]、探測壓力傳感器的變形[5]或者采用附著在光纖束末端的FP(Fabry-Perot)聚合物薄膜作為超聲傳感器[6]；第二，提高成像速度，例如：通過提高脈沖激光光源的重復頻率，加快光聲信號的產生過程，縮短信號采集的等待時間[7]，或者提高光聲信號的采集速率從而節省數據的采集時間[8]等；第三，成像分辨率從超聲分辨水平發展到了光學分辨水平[9]。

PAT成像的逆問題包括聲學和光學兩方面：聲學逆問題是指根據探測器采集到的光聲信號(本質是超聲波)重建組織內部的初始聲壓分布或空間光吸收能量密度，即一般意義上的光聲圖像重建[10-12]；光學逆問題是指運用合適的光傳輸模型與優化算法，根據探測到的光聲信號或者光吸收能量密度，估算出組織的光學特性參數(包括光吸收系數和散射系數)的空間分布[13]和熱膨脹特性參數(Gruneisen系數)等[14-16]，得到對組織光學特性的定量評價，即定量光聲層析成像(Quantitative photoacoustic tomography,qPAT)。由于聲波在組織中傳播的時間比激光照射組織以及組織吸收光的時間長約3個數量級，因此可以將聲學逆問題和光學逆問題分離開來分別求解[16]。聲學逆問題的重建結果，即光吸收能量密度是由局部的光吸收系數和光子數分布共同決定的，并不能反映組織的光吸收系數分布，而光吸收系數與組織的化學成分密切相關，正常和病變組織的光學特性參數之間通常有較明顯的差異，因此qPAT可為疾病的早期診斷提供更加準確可靠的信息。

目前對qPAT的研究已成為光聲成像領域的熱點之一，尤其是同時重建光吸收系數和散射系數的空間分布。本文在簡介光聲成像和qPAT原理的基礎上，對目前已提出的主要qPAT算法進行總結和歸納，簡介其中典型算法的原理，并討論各自的優勢和不足。

2 光聲成像的原理

生物PAT成像是一種以超聲波作為媒介、以組織的光吸收系數和散射系數作為成像參數的生物光子成像方法，其物理基礎是生物組織的光聲效應[3]。成像系統包括3個組成部分：光聲信號的產生單元、接收單元和后處理單元。一束短脈沖(～10 ns)激光經過光學元件后照射到生物組織上，在組織內部形成與組織光學特性參數相關的能量沉積分布。由于激光脈寬很窄，組織吸收的光子能量不能在短時間內釋放，導致組織溫度瞬間的不均勻提升。周期性熱流使周圍的介質產生熱膨脹從而激發出寬頻帶的超聲波，并迅速向組織邊界傳播。基于這種超聲波信號的特殊產生機理，為了區別于其他的超聲信號，通常稱其為光聲信號[17]。超聲換能器接收到光聲信號之后，經計算機處理即可重建出組織內部光能量沉積的分布圖，揭示病變組織的內部信息。

如圖1所示，從組織內的吸收體吸收光子到探測器測得聲壓時間序列的整個過程稱為光聲成像的正問題，可分為光學正問題和聲學正問題兩部分：前者的結果是光吸收能量密度，后者的結果是探測器測得的聲壓信號。假設采用單一波長λ的光源照射組織，組織的光吸收系數和散射系數分別為μa和μs，待測組織區域Ω內一點r處的光吸收能量密度H(r,λ)為

H(r,λ)=μa(r,λ)Φ(r,λ;μa(r,λ),μs(r,λ)),

(1)

其中，H(r,λ)定義為單位體積單位時間內的熱能轉換；r∈Ω，Ω?Rn(Rn為n維實數空間，n=2,3)為有界域，Φ是光能流率，則r處的初始聲壓為

(2)

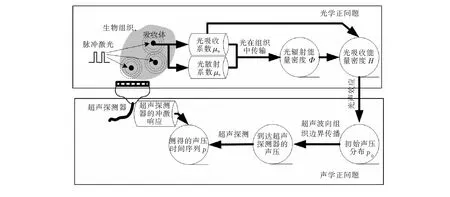
圖1 光聲成像正問題框圖Fig.1 Photoacoustic imaging block diagram of the forward problem

3 定量光聲成像的原理

3.1 聲學逆問題

假設介質的聲學特性均勻，在理想激光脈沖的均勻照射下，被照組織產生的三維光聲信號的幅值與脈沖激光的幅值成正比，光聲信號的特性由光能量的吸收分布決定。因此，可以根據探測器測量到的聲壓時間序列p(r,λ,t)重建初始聲壓的空間分布p0(r,λ)，進而得到光吸收分布H(r,λ)，即PAT聲學逆問題，也就是通常所說的光聲圖像重建。

如果超聲波在密度均勻的無損介質中的傳播速度是均勻的，并且光激發可被看作是瞬時的，那么超聲波傳播的物理模型可由以下3個方程表示[9]：

(3)

式中，p(r,t)為r∈Ω?Rn處、t∈R+時刻的聲壓；u(r,t)為介質的振動速度；c為聲速；ρ(r,t)為位置r處、時刻t時的聲學密度；ρ0是介質密度。

從不同的應用角度出發，借鑒其他成像技術，研究者已提出了多種圖像重建算法，例如濾波反投影法(Filtered back-projection,FBP)、時間反演法(Time-reversal,TR)、相控聚焦算法、基于傅里葉變換的重建算法、反卷積重建算法和迭代重建算法等[12]。

3.2 光學逆問題

PAT光學逆問題是指由初始聲壓分布p0(r,λ)估算組織的光吸收系數和散射系數的空間分布。在早期的研究中，通常假設組織的光散射系數是已知的，那么采用遞歸法[18]或者非遞歸的方法[19]即可重建出光吸收系數的分布。但是，該假設在多數情況下都是不成立的，更為通用的方法是基于誤差最小化的方法。由式(2)可知，若待測組織內部的光吸收系數和散射系數是有界常數且滿足Lipschitz連續，且已知Gruneisen系數，光吸收能量密度的測量值為

(4)

那么，光學逆問題可表述為如下的非線性最小二乘問題[20-21]

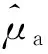
C·H(r,λ;μa(r,λ),μs′(r,λ))‖2)， (5)

其中，μs′是組織的約化散射系數

μs′=μs(1-g)，

(6)

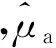
光能流率Φ是未知的，而且它與組織的光吸收系數和散射系數有關，同時PAT成像是三維高分辨率成像，所涉及的數據量極大，因此由光吸收能量密度的測量值重建組織的光學特性參數是一個大規模的非線性不適定問題，特別是當同時重建光吸收系數和散射系數時[22]。

求解光學逆問題需要解決兩個關鍵問題[20]：第一，建立光在組織中傳輸的前向模型，模型的輸出就是光吸收能量密度的理論值；第二，選擇適當的優化策略，使光吸收能量密度的測量值與前向模型的輸出值之間的誤差最小，進而得到光學參數的估計值。

3.3 光在組織中傳輸的前向模型

通常采用輻射傳輸方程(Radiative transfer equation，RTE)描述光子在混濁介質中的遷移過程[22]。RTE是積分-微分方程，求解時常需要在空間域和角度域內對方程進行離散化，步驟較為繁瑣，因而通常對其進行擴散近似(Diffusion approximation，DA)。相比于DA，RTE能夠更準確地描述光子在組織中的遷移過程，尤其是在非擴散區域，但是其復雜的求解過程和較高的運算成本限制了它的廣泛應用。

3.3.1 輻射傳輸方程

RTE描述了在特定控制體(Control volume)內的能量守恒：當光在待測區域內沿某一方向傳輸時，組織對光子的吸收、偏離光傳輸方向上光子的散射和超過待測區域的光子外流出都會導致能量的損失，而沿光傳輸方向的光子散射或介質中的其他光源又會造成能量的增加。

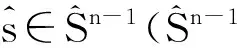
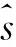
(7)

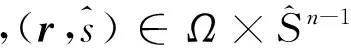
(8)

假設除了光源Γs??Ω處以外，在待測區域邊界?Ω處光子不會向內傳輸，那么方程(7)的邊界條件是

(9)

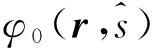
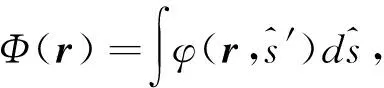
(10)

其中，Φ是光能流率，也稱為光輻射通量。

3.3.2 擴散近似

假設組織的約化散射系數遠大于吸收系數，即光在組織中發生散射的幾率遠高于吸收(對于人體的大多數組織，該假設是成立的)，并且光在組織中的傳輸和分布近似于各向同性，則可將RTE簡化為擴散方程(Diffusion equation,DE)，它是用球諧函數表示的RTE的一階相位近似。

在DA模型中，光子密度被簡化為只與空間變量r有關，設有界域Ω的光滑邊界為Γ，則滿足Robin邊界條件的時間獨立的DE可寫作[14,20]

-·(D(r)Φ(r))+μa(r)Φ(r)=S(r),r∈Ω，

(11)

其中，S(r)是源項，D(r)是擴散系數：

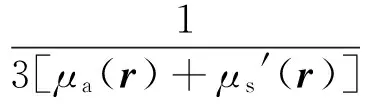
(12)

為了求式(11)的數值解，需要確定適當的邊界條件。例如可采用Dirichlet邊界條件[20]，即在外推邊界處(距離介質邊界2D處)，令Φ=0。計算出Φ(r)后，則

H(r)=μa(r)Φ(r),

(13)

DE的求解方法相對較簡單，只需在空間域內對方程離散化即可，因而它是目前qPAT中最常用的前向模型[14]。在較為理想的情況下，例如各向同性的渾濁介質中嵌入柱狀的不均勻物質，求解DE可以得到光吸收能量密度的解析解[24]。對于實際的生物組織，則需要采用有限差分法或者有限元法得到DE的數值解。

DA僅在擴散域內有效，即在距離光源幾個遷移平均自由程(Transportmeanfreepaths)的區域內μa=μs′，在該區域內光由于發生多次散射，因而失去方向性而擴散開。但是對于PAT成像，接近光源的區域和待測區域的邊界構成了圖像的重要組成部分，通常包含診療疾病所需的重要信息，在這些區域內，光的傳輸是高度各向異性的，因此DA是不成立的[23]。

3.4 主要的優化方法

為了得到光在組織中傳輸的前向模型的數值解，一般需要先對其進行有限元離散化，相比一般的單網格方法，采用雙網格方法可在保證重建精度的前提下，明顯縮短重建時間，提高計算效率[20,25]。在此基礎上求解式(5)的非線性最小二乘問題，使光吸收能量密度的測量值與其理論值之間的均方誤差最小，即可求得光吸收系數和散射系數的空間分布。最常用的方法是Levenberg-Marquardt(LM)方法[26]，即L2范數Gauss-Newton法[27]，通過計算Hessian矩陣的逆矩陣，可迭代地調整(μa,μs)的值。但是該計算過程非常耗時，因此出現了近似計算逆Hessian矩陣的算法，主要包括基于Jacobian矩陣的線性方法[21,28]、非線性梯度法[23,14,29-32]、Bregman迭代法[15]等，那么光學逆問題解的精度將很大程度上取決于所選數值模型的精度。

3.4.1 基于Jacobian矩陣的線性方法

考慮到Gauss-Newton法存在運算成本過高的問題，可采用吸收系數和散射系數的Jacobian矩陣構建Hessian矩陣的近似矩陣，用于在Gauss-Newton迭代中更新(μa,μs)的值。此類方法的優點是原理簡單，易于實現，而且它保留了Gauss-Newton法的二階收斂性。但是，PAT是三維成像，數據量巨大，因此得到的Jacobian矩陣是大型密集矩陣，對計算速度和存儲空間的要求都很高，而且計算該密集矩陣的逆矩陣也非常耗時，可能降低此種方法的實用性[23]。文獻[27]提出一種無矩陣(Matrix-free)求解近似Hessian矩陣的方法，即只計算矩陣向量積，可降低對存儲空間的要求，可是計算量仍然很大。

3.4.2 非線性梯度法

此類方法采用基于梯度的擬牛頓(Quasi-Newton)最小化法[33-35]求解式(5)的最優化問題，避免計算Jacobian矩陣和Hessian矩陣，而只需計算式(5)中誤差函數的梯度，從而迭代更新光吸收系數和散射系數的值。通常需要引入正則項，降低問題的病態性，使之成為良態問題，如L2正則化。采用多位置激光照射的方法采集多個光聲信號數據集，在已知Gruneisen系數的前提下，采用此類方法可同時、唯一地確定光吸收系數和散射系數。與基于Jacobian矩陣的方法相比，該類算法具有超線性收斂性，且計算速度快，所需的存儲空間小，對三維圖像的重建更具實用性。但是其計算較復雜，一般需要較多的迭代次數。

3.4.3 正則化方法

對于病態問題，采用正則化方法(即引入正則項)可降低問題的病態程度，把非線性問題轉化為某種條件下的線性問題。因此在解決qPAT這一非線性病態逆問題的過程中，選取合適的正則化方法可使算法更加簡單，保證穩定近似解的存在[36]。對正則化方法的選取依賴于光吸收系數和散射系數的先驗知識。

(1) L1和L2正則化法

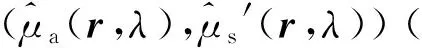
(2) Tikhonov正則化方法

基于變分原理的Tikhonov正則化方法[39]是研究不適定問題的最重要的正則化方法之一，即在求解過程中結合解的某些已知信息對解進行限制。PAT是對不同的組織區域進行成像，因此對組織結構光滑性的約束也不同，這一信息可用于設定Tikhonov方法中解的光滑性假設，反映光學參數的光滑性[36]。對于光滑(連續)變化的光學參數，可采用標準Tikhonov正則化方法[39]，設定解的光滑性，反映光學參數的光滑性。PAT非常適合于對血管這種非光滑性的結構進行成像，這種情況下，將組織的光吸收系數和散射系數看作是分段連續的函數更為適合[40-42]，文獻[36]設計了一種基于標準Level-set[43]的正則化方法，求解分段連續的光吸收系數和散射系數。此外，還可以考慮采用迭代的正則化方法[44]。

(3) 基于全變差(Total-variation,TV)的非光滑正則化方法

對于待求光學特性參數是分段常數的情形，帶約束的全變差(或全變分)正則化方法比L2正則化法更為適合[15,21]，全變分項可以良好地約束信號的平滑性。如果將TV與Bregman方法相結合，則解的精度和計算效率都會得到大幅提升。

3.4.4 Bregman迭代法

Bregman迭代法采用基于次梯度[45]的最小化法求解式(5)的最優化問題，基本模型是ROF(Rudin-Osher-Fatemi)模型。該方法可以解決非線性的非凸優化問題，把非凸問題轉換成凸問題去逼近，通常需結合其他優化方法。

目前，Bregman迭代法在qPAT中的應用還處于初步研究階段。基本思路是：設定光吸收系數和散射系數的初值為0，在每次迭代過程中通過更新次梯度極小化Bregman距離[45]，達到目標函數最小化，最終得到光吸收系數和散射系數的最優解。該算法的計算效率高、收斂速度快。引入正則化后，正則化參數是不變的，且在迭代過程中系統穩定。

在qPAT中常采用以下兩種Bregman迭代法求解最優化問題[15]：

(1)基于Jacobian矩陣的線性Bregman迭代法

采用吸收系數和散射系數的Jacobian矩陣構建Hessian矩陣的近似矩陣，用于在Bregman迭代法中迭代更新吸收系數和散射系數的值。在每次迭代過程中求解的是關于Jacobian矩陣的誤差函數最小值，比直接計算Jacobian矩陣簡單。也可將TV正則化與Bregman迭代法結合，在目標函數中增加由當前迭代過程產生的誤差(其初始值為0)，用于修正下一次迭代，可提高結果的精度，但會增加迭代次數。

(2)基于梯度的Bregman迭代法

若式(5)可微，則可對式(5)采用L-BFGS(limited-memory BFGS)算法[15]得出光吸收系數和散射系數的初值，再引入正則化，進而進行Bregman迭代求解。L-BFGS算法通過對吸收系數和散射系數加權，克服同時重建吸收系數和散射系數對其梯度數據的敏感度問題，所需要的存儲空間小。

4 定量光聲成像的主要算法

4.1 按照PAT成像光源的不同分類

根據PAT成像時所用激光光源的不同可將qPAT方法分為單光源、多光源和光譜qPAT 3類。

(1)單光源qPAT

采用單一波長的單個激光光源照射組織，在已知待測組織的光散射系數分布的情況下，可以重建出光吸收系數的空間分布。若未知組織的內在散射特性，則不能唯一、準確地同時重建出光吸收參數和散射系數的分布[15]。

(2)多光源qPAT(Multiple-source，MS-qPAT)[14,28,34,46-51]

采用相同波長、不同位置的多個激光光源照射組織，采集多個光聲信號數據集，進而得出多個初始聲壓數據集。在已知待測組織的Gruneisen系數的情況下，可唯一、準確地同時重建出待測組織邊界和內部的光吸收系數和散射系數的空間分布。

(3)光譜qPAT[16,19,30,52-54]

采用多波長的激光光源在不同位置照射生物組織，獲得多個初始聲壓數據集，在已知待測組織的光散射特性與入射光波長之間關系的前提下，可唯一地同時重建出光吸收系數、散射系數和Gruneisen系數的空間分布。其中求解光吸收系數和散射系數是非線性問題，求解Gruneisen系數是線性問題。此類方法的缺點是在每次不同波長的激光照明時都需要重新測量初始聲壓分布圖，計算繁瑣。

4.2 按照所用數據源的不同分類

根據重建光學特性參數時所用數據源的不同，可將qPAT算法歸結為兩步算法和一步算法兩大類，其中對兩步算法的研究和優化是目前的主流。

4.2.1 兩步算法

兩步算法指在得到聲學逆問題結果的基礎上，再求解光學逆問題。即假設從探測器采集到的聲壓時間序列中重建出的光吸收能量密度或初始聲壓分布是已知的，在此基礎上求解光學參數的空間分布。

目前已提出的多數qPAT算法都屬于兩步算法，其基本思想如§3.2～§3.4中所述，首先建立光在組織中傳輸的前向模型(如RTE或者DA[21,47,55])，并對其進行有限元離散化，然后采用適當的優化算法使光吸收能量密度的測量值與其理論值之間的均方誤差最小，求得光吸收系數和散射系數的空間分布。通過對光吸收能量密度進行尺度變換(如對數化處理)[21]，可以大大提高優化算法的收斂速度。但是qPAT測得的光強度的動態范圍可能非常大，需要優化尺度變換的比例，以確保最優化問題數值解的穩定性。為了得到聲速不均勻情況下的解，可采用不同波長的激光對組織進行照射，即MS-qPAT，利用采集到的多個光聲信號數據集重建光吸收系數，在這個過程中超聲波的傳播速度是可以求解的。

矢量場法[48,53-54]也屬于兩步算法，其基本思想是：用相同波長的激光光源從兩個不同位置照射組織，收集兩個光聲信號數據。假定聲速均勻，待測區域內組織的Gruneisen系數以及邊界處的光吸收和散射系數是已知的，待測組織內部的光吸收系數和散射系數是有界常數且滿足Lipschitz連續，組織吸收的光子能量全部轉化為初始聲壓。通過建立基于Dirichlet邊界條件的DA模型，將根據兩個初始聲壓數據集構建的向量場代入光擴散方程，通過等量變換，求解出光吸收系數和散射系數。該算法的優點是：把一個非線性問題分解成兩個線性問題，非迭代地求解光學參數，計算速度快且高效。其局限之處在于：需在待測區域的邊界光散射系數已知的情況下才能使用；只能解決滿足Dirichlet邊界條件的光散射問題；不能同時確定地重建光吸收系數、散射系數和Gruneisen系數，但假定待測區域的某一系數值已知時，可以唯一地確定另外兩個系數。

混合數值重建法[53-55]是在矢量場法的基礎上優化而來的，原理是：假定組織的Gruneisen系數是一個不確定的常數，聲速均勻，被測組織吸收的光能量全部轉化為初始聲壓。通過擴散光學層析(Diffuse optical tomography,DOT)成像模型獲取待測區域的邊界光吸收系數和散射系數。建立基于Dirichlet邊界條件的DA模型，采用非線性最優化方法[36,49,55]更新邊界光吸收系數和散射系數。采用矢量場法求解出區域內部的光吸收系數和散射系數，并迭代更新，直至通過RTE和DA模型生成的數據與實測數據一一匹配。該算法除了具有矢量場法的優點以外，由于用非線性優化問題來處理PAT逆問題，因而減小了未知空間，而利用矢量場法可以減小優化范圍；結合DOT成像，求解出待測區域的邊界系數值，克服了矢量場法的缺陷。

此外，可以利用DOT成像測得光能流率[56]，或者利用已知光吸收譜的光學對比劑來定量測量待測組織上的局部光能流率[57]。將PAT與聲光調制結合起來，亦可去除初始聲壓測量中光能流率的影響[58]。

兩步算法的主要不足在于：根據探測器接收的光聲信號重建光吸收能量分布是存在誤差的，所以在此基礎上重建出的光學參數也是不準確的；超聲波在組織內的傳播速度是變化的，并不能準確獲得聲速，而兩步算法僅在聲速已知的情況下重建光學參數的誤差較小；光學噪聲和光散射問題也是不可忽略的。

4.2.2 一步算法

一步算法指根據超聲探測器接收到的組織產生的光聲信號直接重建光學特性參數，包括一步反演算法[59]、單級法[60]和免校正法[61-62]等。

一步反演算法的基本思想是采用相同波長、不同位置的光源照射待測組織，采集多個聲壓數據集 。假定已知組織的光散射系數和Gruneisen系數，將求解光吸收系數分布的逆問題分為線性和非線性兩種情況分別進行分析。對于線性逆問題，假定已知背景組織的光吸收系數，采用Born近似法[63]和Landweber迭代法[64]，求解待測組織和背景組織的光吸收系數之間的差值，進而重建光吸收系數分布。這種方法一般適用于聲速變化且未知、光吸收系數的變化相對較小的情況。對于非線性逆問題，采用最優控制法，設定一個目標函數，用Levenberg-Marquardt方法使目標函數最小，求解光吸收系數的最優解。在不同組織的邊界處，超聲波傳播速度和組織光學系數的相對變化一般較小，因而可以看作是線性逆問題。該算法的優點是：可在超聲波速未知的情況下求解光吸收系數，同時還可以求解出超聲波的傳播速度。但是不能同時重建光吸收系數、散射系數和Gruneisen系數[52]。

單級法的基本思想是在單一波長、不同位置的激光照射條件下[53]，采集超聲探測器產生的聲壓數據集。假設已知Gruneisen系數，且聲速均勻，使用RTE前向模型，采用有限元離散化；在包含成像目標的封閉區域內，使用廣義Tikhonov正則化方法[39]求解出RTE算子參數；使用近端梯度算法使Tikhonov函數最小化重建光吸收系數。在已知光散射系數的情況下，利用該方法可以唯一地重建出光吸收系數。也可在不同波長的激光照明條件下，利用該算法重建光學參數。

免校正法的原理是：假設待測區域內的介質均勻且已知光散射系數，采用有限元離散化的方法，使用DA前向模型，根據待測邊界的聲壓測量值和計算結果得出光吸收系數的測量值；然后，使用牛頓法和Marquardt-Tikhonov正則法[42]迭代更新光吸收系數，尋找目標函數最小化的最優值，重建出光吸收系數分布圖。該算法的優點是它僅利用聲壓的歸一化邊界測量值和入射光的強度，不依賴于任何校正程序；采用標準光聲數據，消除了超聲探測器靈敏度的影響。此外，還可以將該算法應用于光譜光聲測量中。

4.2.3 小結

兩步法需要首先根據光聲信號重建組織內部的光吸收能量分布或光聲壓分布圖，再據此重建組織的光學參數。在早期的研究中，多采用一種波長的激光照射組織進行光聲成像。在后續的研究中發現，不同波長的激光照射組織形成的光吸收能量分布和光聲壓分布圖不同，這樣會增加重建光學參數時的變量。對于光譜qPAT問題，也可以采用兩步算法解決，分別使用多種波長的激光照射組織，再重復多次重建過程，但這樣會使步驟過于繁瑣，延長重建過程。目前對兩步算法的優化主要是針對光譜qPAT或者MS-qPAT。由于使用不同光源照射時，生物組織的光學參數是不會改變的，因而對于MS-qPAT，采用一步算法重建光學參數可解決上述兩步算法的重建過程中變量增加的問題，相對較準確地重構組織的光學參數。此外，探測器采集的光聲信號是通過測量區域的邊界部分獲得的，據此重建出的初始聲壓分布圖是不準確的，進一步重建出的光學參數也存在較大誤差，采用一步算法則可以避免重建初始聲壓分布圖時產生的誤差，重建出相對較準確的光學參數。

5 結 論

PAT成像為研究生物組織的形態結構、生理和病理特征以及代謝功能等提供了重要的手段。生物組織的光吸收特性與其結構功能和病理特征等緊密相關，qPAT根據生物組織產生的光聲信號恢復其光學特性參數，是一個大規模、非線性、病態的逆問題。

目前，qPAT面臨的挑戰主要包括：(1)聲學方面，進一步提高重建圖像的精度。(2)光學方面，在多波長激光照射下實現參數重建，考慮未知波長的依賴性影響，以及全面求解光學和聲學逆問題的規模。(3)目前的研究工作多是側重在相對理想的條件下重建組織的光學參數，需進一步考慮實際情況的復雜性，例如組織Gruneisen系數的變化、超聲波在組織中的非勻速傳播、光在組織表面的非均勻分布以及噪聲等，使重構出的光學參數分布圖更接近真實情況。(4)將二維圖像重建算法擴展到三維，恢復出光學參數的三維分布圖。(5)從數學計算的角度來講，要實現對光吸收系數和散射系數空間分布的高分辨率重建，所需的計算成本非常高，尤其是重建光學參數的三維空間分布時，對計算機的存儲空間和運行速度都有很高的要求。

除了光學參數之外，光聲成像還能利用其他成像參量進行多尺度成像，例如：化學參量成像、黏彈參量成像、溫度參量成像、速度參量成像、聲學功率譜參量成像和物化譜參量成像等[65-66]，為疾病的臨床診治提供更為豐富的組織結構和功能信息。

[1] YAO J,WANG L V.Breakthroughs in photonics photoacoustic tomography [J].IEEEPhoton.J.,2014,6(2):0701006.

[2] NAM S Y,CHUNG E,SUGGSL J,etal..Combined ultrasound and photoacoustic imaging to noninvasively assess burn injury and selectively monitor a regenerative tissue-engineered construct [J].TissueEng.Part C:Methods,2015,21(6):557-566.

[3] WANG L V,GAO L.Photoacoustic microscopy and computed tomography: from bench to bedside [J].Annu.Rev.Biomed.Eng.,2014,11(16):155-185.

[4] NUSTER R,GRATT S,PASSLER K,etal..Photoacoustic section imaging using an elliptical acoustic mirror and optical detection [J].J.Biomed.Opt.,2012,17(3):99-106.

[5] LAUFER J,JOHNSON P,ZHANG E,etal..Invivopreclinical photoacoustic imaging of tumor vasculature development and therapy [J].J.Biomed.Opt.,2012,17(5):449-450.

[6] ANSARI R,ZHANG E,MATHEWS S,etal..Photoacoustic endoscopy probe using a coherent fiber-optic bundle [J]SPIEBios.,2016,142 (10):97080L

[7] BILLEH Y N,LIU M,BUMA T.Spectroscopic photoacousti microscopy using a photonic crystal fiber supereontinuum source [J].Opt.Express,2010,18(18):18519-18524.

[8] MALONE E,POWELL S,COX B T,etal..Reconstruction-classification method for quantitative photoacoustic tomography [J].J.Biomed.Opt.,2015,20(12):126004.

[9] SONG H,WANG L V.Optical-resolution photoacoustic microscopy auscultation of biological systems at the cellular level [J].Biophys.J.,2013,105(4):841-847.

[10] LUTZWEILER C,DEN-BEN X L,RAZANSKY D.Expediting model-based optoacoustic reconstructions with tomographic symmetries [J].Med.Phys.2014,41(1):013302.

[11] KUCHMENT P,KUNYANSKY L.Mathematics of photoacoustic and thermoacousic tomography [J].Eur.J.Appl.Math.,2009,2(19):817-866.

[12] 孫正,韓朵朵,王健健.血管內光聲成像圖像重建的研究現狀 [J].光電工程,2015,42(3):20-27.SUN Z,HAN D D,WANG J J.Review of image reconstruction for intravascular photoacoustic imaging [J].Optoelect.Eng.,2015,42(3):20-27.(in Chinese)

[13] SONG N,DEUMIC C,DAS A.Considering sources and detectors distributions for quantitative photoacoustic tomography [J].Biomed.Opt.Express,2014,5(11):3960-3974.

[14] GAO H,OSHER S,ZHAO H.MathematicalModelinginBiomedicalImagingⅡ [M] Berlin/Heidelberg: Springer,2012 131-158.

[15] GAO H,ZHAO H,OSHER S.Bregman methods in quantitative photoacoustic tomography [J].Cam.Rep.,2010,30(6):3043-3054.

[16] COX B,LAUFER J G,ARRIDGES R,etal..Quantitative spectroscopic photoacoustic imaging: a review [J].J.Biomed.Opt.,2012,17(6):ID 061202.

[17] 孫正,苑園，王健健.血管內光聲成像的研究進展 [J].中國生物醫學工程學報,2015,34(2):221-228.SUN Z,YUAN Y,WANG J J.Progress of intravascular photoacoustic imaging [J]Chin.J.Biomed.Eng.,2015,34(2):221-228.(in Chinese).

[18] COX B T,ARRIDGE S R,KOSTLI K P,etal..Two-dimensional quantitative photoacoustic image reconstruction of absorption distributions in scattering media by use of a simple iterative method [J].Appl.Opt.,2006,45(8):1866-1875

[19] BANERJEE B,BAGCHI S,VASU R M,etal..Quantitative photoacoustic tomography from boundary pressure measurements: non-iterative recovery of optical absorption coefficient from the reconstructed absorbed energy map [J].J.Opt.Soc.Am.A.2008,25(9):2347-2356.

[20] LI S,MONTCEL B,YUAN Z,etal..Multigrid-based reconstruction algorithm for quantitative photoacoustic tomography [J].Biomed.Opt.Express,2015,6(7):2424-2434.

[21] TARVAINEN T,COX B T,KAIPIO J P,etal..Reconstructing absorption and scattering distributions in quantitative photoacoustic tomography [J].InverseProbl.,2012,28(8):1067-1079.

[22] TARVAINEN T.ComputationalMethodsforLightTransportinOpticalTomography[D].Kuopio: University of Kuopio,2006.

[23] SARATOON T,TARVAINEN T,COX B T,etal..A gradient-based method for quantitative photoacoustic tomography using the radiative transfer equation [J].InverseProbl.,2013,29(7):75006-75024.

[24] LI S,MONTCEL B,LIU W,etal..Analytical model of optical fluence inside multiple cylindrical inhomogeneities embedded in an otherwise homogeneous turbid medium for quantitative photoacoustic imaging [J].Opt.Express,2014,22(17):20500-20514.

[25] 肖嘉瑩.定量光聲成像技術及在骨關節炎診斷的研究 [D].長沙:中南大學,2011.XIAO J Y.QuantitativePhotoaeoustieTomographyandItsApplicationtoTheDiagnosisofOsteoarthritis[D] Changsha: Central South University,2011.(in Chinese)

[26] KUCHMENT P.TheMathematicalLegacyofLeonEhrenpreis[M].Milan: Springer,2012:183.

[27] SCHWEIGER M,ARRIDGE S R,NISSILA I.Gauss-Newton method for image reconstruction in diffuse optical tomography [J].Phys.Med.Biol.,2005,50(10):2365-2386.

[28] COX B T,TARVAINEN T,ARRIDGE S.Multiple illumination quantitative photoacoustic tomography using transport and diffusion models [C]ProceedingsofInternationalConferenceonTomographyandInverseTransportTheory,USA,MathematicalSoc.,2011.

[29] COX B T,ARRIDGE S R,BEARD P C.Gradient-based quantitative photoacoustic image reconstruction for molecular imaging [C].ProceedingsofSPIEInternationalConferenceonPhotonsPlusUltrasound:ImagingandSensing.SPIE-IntSoc..OpticalEngineering，SanJose,California,UnitedStates,2007.

[30] BAL G,REN K.On multi-spectral quantitative photoacoustic tomography in diffusive regime [J].InverseProbl.,2012,28(2):025010-25022.

[31] MAMONOV AV,REN K.Quantitative photoacoustic imaging in radiative transport regime [J].Commun.Math.Sci.,2012,12(2):201-234

[32] SOONTHORNSARATOON T.Gradient-basedMethodsforQuantitativePhotoacousticTomography[D].London: University College London,2014.

[33] NOCEDAL J.NumericalOptimization(SpringerSeriesinOperationsResearchandFinancialEngineering)[M].New York: Springer,2006:134.

[34] BAL G,Uhlmann G.Inverse diffusion theory of photoacoustics [J].InverseProbl.,2009,6(8):1407-1426.

[35] KLOSE A,HIELSCHERA H.Optical tomographic image reconstruction with quasi-Newton methods [J].InverseProbl.,2003,19(2):387-409.

[36] CEZARO A D,CEZARO F T D.Regularization approaches for quantitative photoacoustic tomography using the radiative transfer equation [J].J.Math.Anal.Appl.,2015,429(1):415-438.

[37] GAO H,ZHAO H.Multilevel bioluminescence tomography based on radiative transfer equation Part 1: l1 regularization [J].Opt.Express，2010,18(3):1854-1871.

[38] GAO H,ZHAO H.Multilevel bioluminescence tomography based on radiative transfer equation Part 2: total variation and l1 data fidelity [J].Opt.Express,2010,18(3):2894-2912.

[39] GRASMAIR M,GROSSAUER H,Haltmeier M,etal..VariationalMethodsinImaging[M].New York: Springer,2009：294.

[40] NEATER W,SCHERZER O.Quantitative photoacoustic tomography with piecewise constant material parameters [J].SIAM.J.ImagingSci.,2014,7(3):1755-1774.

[41] BERETTA E,MUSZKIETA M,NAETAR W,etal..A variational method for quantitative photoacoustic tomography with piecewise constant coefficients [J].PreprintArXiv,2015:1509.04982.

[42] CEZARO A D,LEITO A,TAI X C.On piecewise constant level-set (pcls) methods for the identification of discontinuous parameters in ill-posed problems [J].InverseProbl.,2013,29(1):015003.

[43] JIANG H,YUAN Z,YIN L,etal..Quantitative photoacoustic tomography: recovery of optical absorption coefficient maps of heterogeneous media [C].SPIE8thConferenceonBiomedicalThermoacoustics,Optoacoustics,andAcousto-optics.PhotonsPlusUltrasound:ImagingandSensing,SPIE-IntSoc.OpticalEngineering,SanJose,California,UnitedStates,2007.

[44] KALTENBACHER B,NEUBAUER A,SCHERZER O.Iterative regularization methods for nonlinear ill-posed problems [C].RadonSeriesonComputationalandAppliedMathematics，Berlin,2008.

[45] ELVETUN O L,NIELSEN B F.The split Bregman algorithm applied to PDE-constrained optimization problems with total variation regularization [J].Comput.Optim.Appl.,2016,64(3):699-724.

[46] AMMARI H,BOSSY E,JUGNON V,etal..Reconstruction of the optical absorption coefficient of a small absorber from the absorbed energy density [J].SIAMJ.Appl.Math.,2011,71(3):676-693.

[47] BERGOUNIOUX M,SCHWINDT E L.On the uniqueness and stability of an inverse problem in photo-acoustic tomography [J].J.Math.Anal.Appl.,2015,431(2):1138-1152.

[48] ZEMP R J.Quantitative photoacoustic tomography with multiple optical sources [J].Appl.Opt.,2010,49(18):3566-3572.

[49] BAL G,REN K.Multi-source quantitative photoacoustic tomography in a diffusive regime [J].Inverseprobl.,2011,27(7):75003-75022.

[50] BAL G,UHLMANN G.Inverse diffusion theory for photoacoustics [J].InverseProbl.,2010，26(8):25021-25032.

[51] SHAO P,HARRISON T,ZEMP R J.Iterative algorithm for multiple illumination photoacoustic tomography (MIPAT) using ultrasound channel data [J].Biomed.Opt.Express,2012,3(12):3240-3249

[52] COX B T,ARRIDGE S R,BEARD P C.Estimating chromophore distributions from multiwavelength photoacoustic images [J].J.Opt.Soc.Am.A,2009,26(2):443-455.

[53] BAL G,JOLLIVET A,JUGNON V.Inverse transport theory of photoacoustics [J].InverseProbl.,2010,26(2):25011-25045.

[54] BAL G,REN K.On multi-spectral quantitative photoacoustic tomography in diffusive regime [J].InverseProbl.,2012,28(2):25010-25022.

[55] REN K,GAO H,ZHAO H.A hybrid reconstruction method for quantitative PAT [J].SIAMJ.ImagingSci.2013,6(1):32-55.

[56] BAUER A Q,NOTHDURFT R E,ERPELDING TN,etal..Quantitative photoacoustic imaging: correcting for heterogeneous light fluence distributions using diffuse optical tomography [J].J.Biomed.Opt.,2011,16(9):096016.

[57] RAJIAN J R,CARSON P L,WANG X.Quantitative photoacoustic measurement of tissue optical absorption spectrum aided by an optical contrast agent [J].Opt.Express,2009,17(6):4879-4889.

[58] DaOUDI K,HUSSAIN A,HONDEBRINK E,etal..Correcting photoacoustic signals for fluence variations using acousto-optic modulation [J].Opt.Express,2012,20(13):14117-14129.

[59] DING T,REN K,VALLELIAN S.A one-step reconstruction algorithm for quantitative photoacoustic imaging [J].InverseProbl.,2015,31(9):65003-65023.

[60] HALTMEIER M,NEUMANN L,RABANSER S.Single-stage reconstruction algorithm for quantitative photoacoustic tomography [J].InverseProbl.,2015,31(6):65005-65028.

[61] YUAN Z,JIANG H B.A calibration-free,one-step method for quantitative photoacoustic tomography [J].Med.Phys.,2012,39(11):6895-6899.

[62] JIANG H B,ZHANG Q Z,YUAN Z,etal..Simultaneous reconstruction of acoustic and optical properties of heterogeneous media by quantitative photoacoustic tomography [J].Opt.Express,2006,14(15):6749-6754.

[63] RONDI L,SANTOSA F.Enhanced electrical impedance tomographyviathe mumford-shah functional [J].EsaimContr.Optim.,2000,6(6):517538.

[64] KIRSCH A.AnIntroductiontoTheMathematicalTheoryofInverseProblems[M].New York: Springer,1996:234

[65] 殷杰，陶超，劉曉峻.多參量光聲成像及其在生物醫學領域的應用 [J].物理學報,2015,64(9):098102.YIN J,TAO C,LIU X J.Multi-parameter photoacoustic imaging and its application in biomedicine [J].ActaPhys.Sinica,2015,64(9):098102.(in Chinese)

[66] 苗少峰,楊虹,黃遠輝,等.光聲成像研究進展 [J].中國光學,2015,8(5):699-713.MIAO S F,YANG H,HUANG Y H,etal..Research progresses of photoacoustic imaging [J].Chin.Opt.,2015,8(5):699-713.(in Chinese)

孫正(1977-)，女，河北保定人，博士，教授，碩士生導師，2004年于天津大學獲得博士學位，主要從事生物醫學信號處理、醫學成像和圖像處理等方面的研究。

E-mail: sunzheng_tju@163.com

Review on Progress of Quantitative Photoacoustic Tomography

SUN Zheng*,ZHENG Lan

(DepartmentofElectronicandCommunicationEngineering,NorthChinaElectricPowerUniversity,Baoding071003,China)

Photoacoustic tomography (PAT),an emerging medical imaging modality,combines the high resolution of ultrasonic imaging and high contrast of optical imaging.Current research on PAT includes two inverse problems,i.e.,constructing the distribution of initial acoustic pressures according to the photo-acoustic signals generated by the tissues and estimating the optical absorption and scattering coefficients of the tissues within the imaging region based on the results of the first inversion.The latter,known as quantitative photoacoustic tomography (qPAT),is in general a nonlinear ill-posed problem.This paper summarizes current algorithms for solving the qPAT inversion.Related advantages and limits as well as perspective studies are discussed.

quantitative photoacoustic tomography (qPAT); image reconstruction; inverse problem; optical absorption coefficient; diffusion coefficient; Gruneisen coefficient

1000-7032(2017)09-1222-11

2017-03-24；

2017-04-27

國家自然科學基金(61372042)； 中央高校基本科研業務費專項資金(2014ZD31)資助項目

O439

A

10.3788/fgxb20173809.1222

*CorrespondingAuthor,E-mail:sunzheng_tju@163.com

Supported by National Natural Science Foundation of China(61372042); Special Fund for Basic Scientific Research Business in Central Universities(2014ZD31)