一種將遞歸過程轉換為非遞歸過程的方法研究

張建波

摘 要：提出一種把遞歸過程轉換為非遞歸過程的方法——遞歸樹法，畫出遞歸過程的遞歸樹，然后通過對遞歸樹的后根序遍歷實現遞歸過程的非遞歸化，最后通過案例說明該方法的可行性和有效性。

關鍵詞：遞歸；遞歸過程；非遞歸化；遞歸樹

0 引 言

遞歸有思路清晰、代碼簡潔、易于理解等特點，是很多算法設計策略（如分治、回溯等）的核心內容，但是遞歸過程在計算機中實現時需要多次調用自身，增加了時空開銷。很多學者對遞歸過程進行了深入研究[1-4]，部分學者提出了一些遞歸過程的非遞歸化方法[4]。文獻[3]和[5]雖然能很好地描述遞歸過程，但沒有給出如何轉換為非遞歸過程的一般方法；文獻[4]提出了模仿法，該方法從簡單實例入手，逐步過渡到較復雜的遞歸算法，初學者容易理解，但不能對復雜的遞歸過程進行直觀分析。

由于遞歸樹[2-3]作為研究遞歸過程的一種圖形化方法，具有直觀、簡單等特點。筆者在此基礎上提出一種基于遞歸樹的遞歸過程的非遞歸化方法，該方法通過對遞歸樹后根序遍歷的思想實現遞歸過程的非遞歸化，具有直觀、易于理解的特點。

1 遞歸與遞歸樹

1.1 遞歸及遞歸過程的設計

一個問題的解法可以通過把該問題劃分成若干子問題，若子問題比較簡單，則直接求解；否則，采用與原問題相同的方法對這些子問題進行再劃分、求解，依次類推，直到子問題變得較為簡單，可以直接求解，當求出所有子問題的解后再對其進行匯總即可得到原問題的解，則稱該問題為遞歸問題[5]。在計算機上，人們通常采用遞歸方法來求解遞歸問題，設計出的算法稱為遞歸算法。

在遞歸方法中，遞推動作和結束條件是兩個重要組成部分。結束條件是指子問題比較簡單、不必再劃分成若干更小的子問題時應滿足的條件，也就是說，當子問題滿足結束條件時可以直接求解。當子問題不滿足結束條件，還需要劃分成更簡單的子問題時需要執行的操作步驟稱為遞推動作。遞推動作必須使遞歸算法能夠逐步到達結束條件。遞歸算法的一般模型為：

algorithm （） {

if （） /* 遞歸的結束條件 */

return （direct value）； /* 直接求解，并返回結果 */

else /* 遞歸 */

return （（parameter exchange））； /* 遞推動作 */

}

遞歸的整個過程可分為兩個子過程：遞推過程和回歸過程。當不滿足結束條件時，遞歸過程需要不斷執行遞推動作的過程為遞推過程；當滿足結束條件時停止遞推動作并沿遞推過程的逆過程進行回溯的過程為回歸過程。遞推過程是對子問題不斷細化使其逐步向結束條件靠近的過程；回歸過程是返回各子問題的結果并匯總直到得出問題最終解的過程。在一些復雜的遞歸算法中，遞推過程和回歸過程是交替出現的。

1.2 遞歸樹及其構建

在計算機中，遞歸調用由若干個子遞歸調用組成，而子遞歸又有更下一層的子遞歸調用，這種逐層調用的軌跡可以用遞歸樹來刻畫。

遞歸樹是一種有序樹，樹根為遞歸算法的入口，根的值為遞歸參數值，如果遞歸參數值滿足結束條件，則開始回歸過程，此時根結點也是葉子結點；否則，遞歸算法需要調用自身若干次，每調用一次就相當于樹根多了一個分支，即產成一棵子樹；每棵子樹也是遞歸樹。

遞歸樹是研究遞歸問題與遞歸算法之間的一座橋梁。在分析具體問題時，我們首先從根結點出發，按照遞歸的遞推過程不斷建立并擴展遞歸樹，當滿足結束條件時，該遞歸樹的根結點就成了葉子結點，然后根據建樹的逆序過程，不斷向根部返回并得到最終解。

與一般的非遞歸算法的分析方法——“單步跟蹤法”不同，遞歸樹可以直觀、清晰地描述遞歸算法的整個過程。對于一般的非遞歸算法，設計者常用單步跟蹤法動態演示算法的執行過程；但在遞歸算法中，由于不同層次遞歸時的參數是不一樣的，對于層數較多、遞推過程和回歸過程交替出現的遞歸算法，“單步跟蹤”法容易導致設計者對當前調用環境中的參數產生混亂，因此，遞歸樹法可以有效避免“單步跟蹤”法的缺點。

2 案例分析

正確設計一個遞歸算法的前提是分析問題、明確具體任務并給出清晰的遞歸定義。接下來，筆者通過兩個案例來說明遞歸樹在研究遞歸算法并把遞歸算法轉換為相應的非遞歸算法中的作用。以下算法均采用類C++程序設計語言進行定義和描述。

2.1 漢諾塔（Tower of Hanoi）問題

用狀態變量（n， A， B， C）表示“把 n 個盤子從A柱，借助于B柱移動到C柱上”。參數n表示當前的盤子數量；參數A、B和C分別為柱子的編號。漢諾塔問題的遞歸解法為：

void Hanoi_R（n， A， B， C） {

if （n == 1）

move （A， C）； /* 相當于 Hanoi（1， A， B， C） */

else {

Hanoi_R （n-1， A， C， B）；

move （A， C）；

Hanoi_R （n-1， B， A， C）；

}

}

用遞歸樹描述該遞歸算法（以n = 3為例），如圖1所示。

圖1直觀地描述了n（= 3）個盤子時的解決方法，其中，遞推動作包括3個步驟，即每個度為3的結點下的3個結點；遞歸的結束條件對應n = 1的結點。

從圖1中可知漢諾塔問題的遞歸樹為3叉樹。其中n為1時表明結點為葉子，可直接求解，不必再遞歸。如果對該3叉樹進行后根序遍歷（此問題只須遍歷葉子結點）可得到整個問題的解。

為了能區別同一結點下的所有子女（Child）的處理次序，把結點結構改為（n， A， B， C， k），其中k表示該結點是其雙親結點的第幾個子女。這樣，漢諾塔問題要解決的問題是（3， A， B， C， 1）對應的解，相應的非遞歸算法如下：

void Hanoi_I（n， A， B， C） {

StackInitialize S； /* 初始化棧 */

StackElement p =： （n， A， B， C， 1）； S.Push（p）； /* 樹根p入棧 */

while（！S.IsEmpty（ ）） {

S.getTop（p）； /* 取棧頂 */

if（p.n == 1） { /* 1） 若棧頂元素的 n 值為 1，*/

S.Pop（p）； move（p.A， p.C）； /* 出棧并輸出相應的解 */

if（p.k == 1） { /* 1.1） 若棧頂元素的 k 值為 1，則 */

p =： （1， p.A， p.C， p.B， 2）； S.Push（p）；/* 其右兄弟（第2步）入棧 */

}

else if（p.k == 2）{ /* 1.2） 若棧頂元素的 k 值為2，則 */

S.getTop（p）；

p =： （p.n-1， p.B， p.A， p.C， 3）； S.Push（p）； /* 其右兄弟（第3步）入棧 */

}

else { /* 1.3） 若棧頂元素的 k 值為3，則 */

/* 1.3.1） 若棧不空且棧頂元素的 k 值為3，向上回溯 */

while（p.k == 3 && ！S.IsEmpty（ ）） S.Pop（p）；

/* 1.3.2） 若棧不空，則k只能為1，此時其右兄弟（第2步）入棧 */

if（！S.IsEmpty（ ）） {

p =： （1， p.A， p.C， p.B， 2）； S.Push（p）；

}

}

}

else { /* 2） 若棧頂元素的 n 值不為 1，則 */

// 該子問題還需要再劃分，把劃分的第1步所對應的結點入棧

p =： （p.n-1； p.A， p.C， p.B， 1）； S.Push（p）；

}

} /* while */

}

2.2 Ackerman函數的計算

Ackerman函數的定義為

可以用狀態變量（m，n）表示函數akm（m， n）的值。由于這是一個遞歸定義，因此很容易用遞歸方法設計出其遞歸解法。

根據Ackerman函數的定義，其遞歸程序如下：

int akm_R（int m， int n） {

if（m == 0） return n+1；

else if（n == 0）return akm_R（m-1， 1）；

else return akm_R（m-1， akm_R（m， n-1））；

}

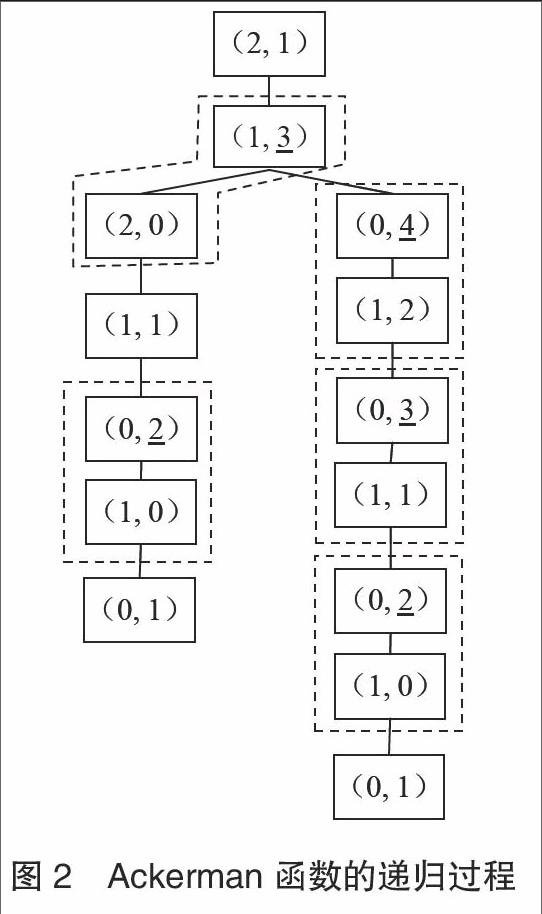
其對應的遞歸樹如圖2所示（以m = 2，n = 1為例），其中虛線框內的結點表示第三種情況（m ≠ 0，n ≠ 0），需要兩次遞歸。

該樹的非遞歸算法如下：

int akm_R（int m， int n） {

StackInitialize S； /* 初始化棧 */

StackElement p =： （m， n）；

S.Push（p）； /* 樹根入棧 */

while（！S.IsEmpty（ ）） {

S.getTop（p）； /* 取棧頂 */

if（p.m > 0 && p.n > 0） { /* 1） 第三種情況，需要兩次入棧 */

S.Push（p.m-1， -1）； /* 1.1） 第1次進棧，用 n == -1 表示其值待求 */

S.Push（p.m， p.n-1）； /* 1.2） 第2次進棧 */

}

else if（p.m > 0 && p.n == 0） /* 2） 第二種情況，入棧一次 */

S.Push（p.m-1， 1）；

else if（p.m == 0） { /* 3） 第一種情況，直接求解并回歸 */

/* 3.1） 出棧，用p表示出棧元素 */

if（！S.IsEmpty（ ））S.Pop（p）；

/* 3.2） 若p中沒有待求項（第一種情況），則直接算出結果并向根部返回 */

if（p.n ！= -1） n = p.n+1；

while（p.n ！= -1 && ！S.IsEmpty（ ）） S.Pop（p）；

/* 3.3） 若p中有待求項，則把結果賦給待求項，入棧，開始新遞歸 */

if（！S.IsEmpty（ ）） { m = p.m； p.n = n； S.Push（p）； }

}

} /* while */

return n；

}

Ackerman函數是一個增長速度很快的函數。在硬件為4G內存、I3-2120 3.30GHz CPU，軟件為Windows 7（64位）操作系統、DEV C++ 5.9.2環境下，以m = 4，n = 1為例，非遞歸算法在約90秒左右的時間里算出結果為65 533，棧里存儲的最大元素個數為1 063 453 415，而遞歸算法因空間資源消耗過大無法算出結果。

3 結 語

在實際中，遞歸問題是一個比較常見的問題，如n皇后問題、迷宮問題、二叉樹遍歷等，而遞歸方法是解決遞歸問題的一個基本方法。利用開發工具（如Visual C++、DEC C++）的調試功能觀察遞歸算法的運行過程往往有較高的難度，特別是對于遞歸層數較高的算法。另外，遞歸算法需要依靠系統提供的遞歸棧來實現多次自身調用，這既耗費時間又耗費空間，因此人們常用迭代或棧來設計相應的非遞歸算法以提高效率，但是對于初學者來說，設計非遞歸算法的難度往往較大。

參考文獻：

[1] 張俊. 基于遞歸樹的遞歸調用分析[J]. 實驗室研究與探索， 2010， 29（3）： 83-87.

[2] 黎遠松. 基于樹的遞歸算法分析技術[J]. 四川理工學院學報（自然科學版）， 2012，25（4）： 50-51.

[3] 周集良. 描述遞歸算法的有效工具： 遞歸樹[J]. 懷化師專學報，1999， 18（5）： 41-44.

[4] 張玉華. 模仿法在數據結構遞歸算法設計中的教學實踐[J]. 計算機教育， 2016（1）： 134-138.

[5] 殷人昆. 數據結構（用面向對象方法與C++語言描述）[M]. 2版. 北京： 清華大學出版社， 2007： 101-102.

（編輯：郭田珍）