開槽實心轉子電機轉子端部系數的計算與比較

黃子果 王善銘 孫宇光 曹海翔 楊占錄，2

(1.電力系統及發電設備控制和仿真國家重點實驗室(清華大學電機系) 北京 100084 2.海軍潛艇學院 青島 266100)

開槽實心轉子電機轉子端部系數的計算與比較

黃子果1王善銘1孫宇光1曹海翔1楊占錄1，2

(1.電力系統及發電設備控制和仿真國家重點實驗室(清華大學電機系) 北京 100084 2.海軍潛艇學院 青島 266100)

開槽實心轉子異步電機轉子的三維非線性渦流場計算量大，常采用二維有限元結合光滑實心轉子端部系數的方法簡化計算。但在轉差率增大時，采用光滑轉子端部系數仿真計算的誤差明顯增大。根據開槽實心轉子渦流分布隨轉差率變化的規律，提出適用于全轉差率范圍的開槽轉子端部系數。依據該端部系數修正轉子電阻率，并采用非線性有限元計算開槽實心轉子電機電磁場，可考慮轉子端部效應以及定、轉子鐵心磁路飽和的影響。在不同工況下，對兩臺不同轉子槽數的開槽實心轉子樣機分別采用不同轉子端部系數進行仿真計算，并與實驗結果比較。該文提出的開槽轉子端部系數的仿真與實驗結果較吻合，且在轉差率較大時，開槽轉子端部系數隨轉子槽數增多而增大。可為準確計算開槽實心轉子電機參數及其設計優化提供依據。

開槽實心轉子 端部系數 二維有限元

0 引言

高速電機轉速高、體積小、功率密度高，可節約電機制造材料。普通疊片轉子的異步電機，轉子表面的線速度上限約為200 m/s，而實心轉子異步電機的轉子表面線速度最大可達約400 m/s[1，2]。實心轉子異步電機具有結構簡單、耐腐蝕、機械強度高、動平衡性能好、可靠性高等優點，特別適用于氣體壓縮機、離心機、分子泵等高速領域[1-4]。采用高速電機直接驅動的系統可省去傳動帶、齒輪變速箱等傳統調速機械裝置，有利于降低系統噪聲，減小系統體積，提高系統效率和可靠性[4]。

早期有學者提出了光滑實心轉子異步電機結構[5]，但光滑實心轉子電機功率因數低，效率低。為此，國內外學者通過轉子軸向開槽、表面覆銅、開槽焊銅、加導電端環等方式改善實心轉子電機的電磁性能[1，2]。

實心轉子表面軸向開槽，結構如圖1所示，開槽影響轉子表面渦流的分布，改變轉子等效阻抗從而增大轉矩[6]。開槽實心轉子中的渦流分布計算較復雜，不僅與定子電流頻率、轉差率相關，還與轉子的電阻率、磁化曲線密切相關。另外，實心轉子端部效應對轉子渦流分布的影響較大。

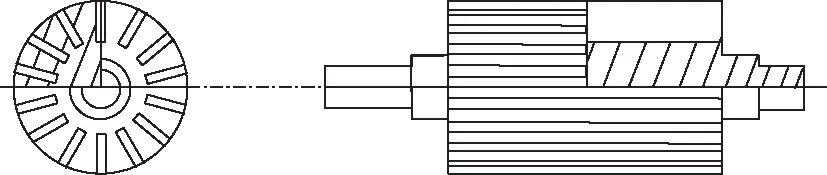
圖1 開槽實心轉子Fig.1 Solid rotor with axial silts

轉子開槽使實心轉子磁場的邊界復雜，二維線性解析解難以求得。轉子電磁場求解區域可以將一個齒槽區作為求解單元[7]或將整個開槽轉子進行等效[5，8]，并采用解析法或磁路法計算轉子等效阻抗參數。開槽實心轉子磁場的解析計算法通常不能計及轉子磁路的非線性，僅用飽和修正系數予以粗略考慮。而二維有限元法可建立實際轉子開槽模型并考慮定、轉子鐵心磁路非線性。二維解析法和有限元法均假設轉子磁場在軸向上的分布規律一致。為考慮開槽實心轉子電機磁場的端部效應，常用端部系數折算二維解析計算的等效轉子阻抗。許多文獻直接使用光滑實心轉子的端部系數近似修正二維計算時的開槽實心轉子電阻率[9-11]，從而考慮端部效應。

文獻[11]采用三維有限元法，假設轉子鐵心線性且氣隙磁通密度的邊界給定，計算開槽實心轉子電機的端部系數，指出了開槽轉子電機的端部系數與光滑實心轉子電機的端部系數并不相同。但對于實心轉子電機完整的三維非線性有限元模型，網格單元數量、矢量場計算量龐大，不適用于電機設計環節。

本文依據開槽實心轉子渦流分布隨轉差率變化的規律，計算開槽實心轉子等效極距，并提出適用于開槽轉子的端部系數。采用有限元諧波場分別結合提出的開槽實心轉子端部系數和現有的不同光滑實心轉子端部系數，計算兩臺不同轉子槽數的開槽實心轉子電機磁場分布，可考慮定、轉子鐵心磁路飽和以及轉子端部效應的影響。采用提出的開槽端部系數的計算結果與實驗結果較吻合，說明了其有效性。

1 光滑實心轉子端部系數比較

考慮開槽實心轉子電機定、轉子鐵心飽和時，需采用有限元法計算。開槽實心轉子電機的三維非線性有限元計算量龐大，不適用于電機設計。許多文獻直接使用光滑實心轉子的端部系數修正轉子電阻率的方法近似考慮實心轉子端部效應[9-11]。常用的光滑實心轉子電機端部系數為D.O′Kelly[12]、W.J.Gibbs[13]、R.L.Russel等[14]、H.Yee[15]、傅豐禮[16]提出的端部系數。

D.O′Kelly提出的光滑轉子經驗端部系數[12]為

(1)

W.J.Gibbs假設轉子的渦流只在鐵心長度以外的端部區域閉合，且氣隙徑向磁通密度沿轉子軸向均勻分布，得到光滑實心轉子的端部系數[13]為

(2)

傅豐禮[16]忽略光滑轉子徑向電流,將定子電流、矢量磁位沿軸向奇延拓并分解為各次諧波,依據轉子三維線性解析求解結果得到轉子端部系數為

(3)

R.L.Russel等提出的光滑轉子端部系數[14]為

(4)

H.Yee分別求解3種不同磁場約束條件的轉子磁場的解，并疊加后得到電機矢量磁位的三維線性解，求得轉子線性條件下的端部系數[15]為

(5)

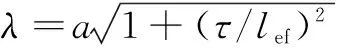
為研究不同轉子槽數的開槽實心轉子端部系數，本文設計了兩臺不同轉子槽數的開槽實心轉子樣機，其主要參數見表1。電機轉子材料為45號鋼，在 15 ℃ 下的電阻率為0.217 8Ω·mm2/m[16]，其磁化曲線參考文獻[17]。

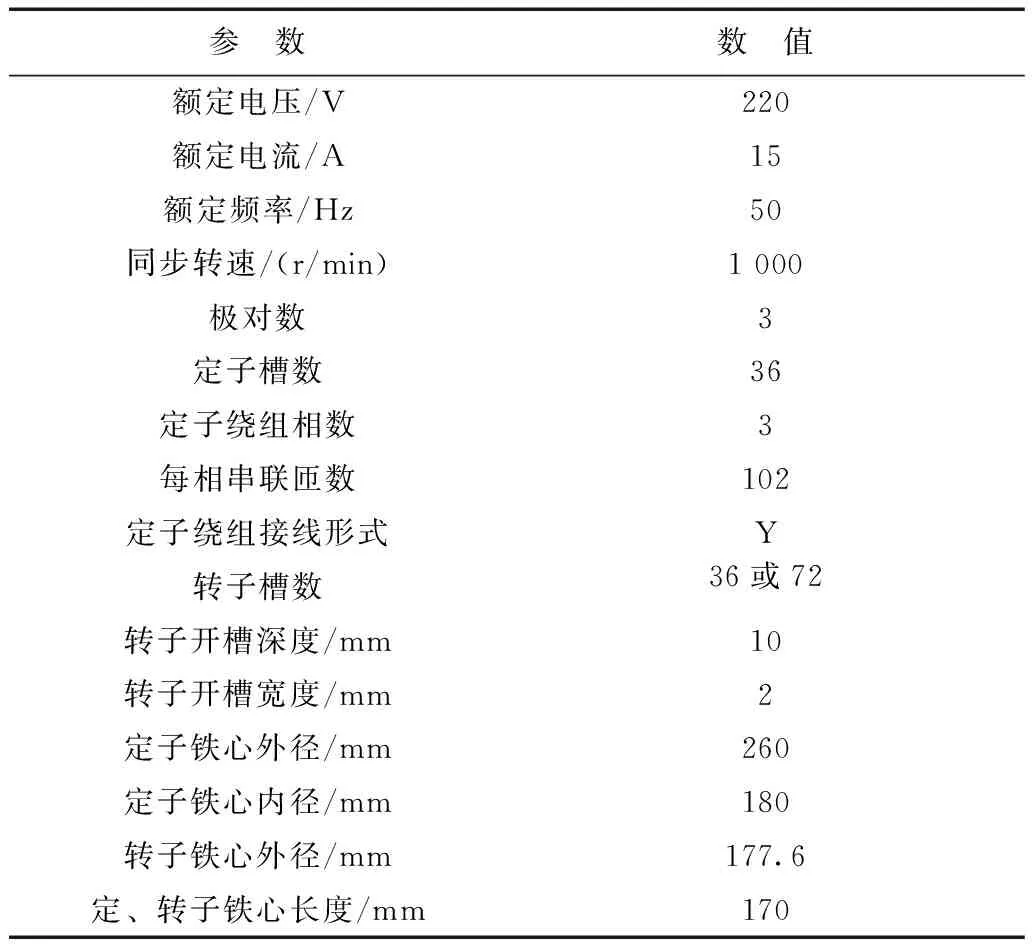
表1 開槽實心轉子樣機主要參數Tab.1 Main parameters of the slit solid rotor motor

二維計算開槽實心轉子電磁場時，若直接使用光滑實心轉子端部系數，根據表1中實驗樣機參數，可計算出式(1)～式(5)五個光滑實心轉子端部系數。繪制這些端部系數隨轉差率變化的曲線如圖2所示。

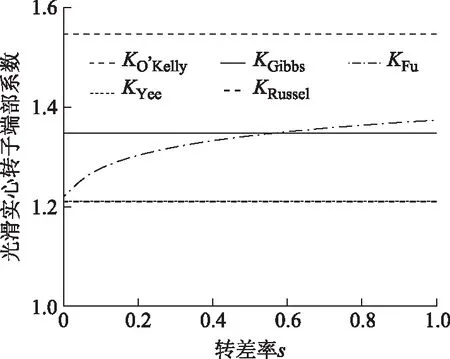
圖2 光滑實心轉子端部系數比較Fig.2 Comparison of different rotor end factors for smooth solid rotor

從圖2中可以看出，端部系數KYee和KRussel的計算結果相等，且在五個端部系數中最小。端部系數KO′Kelly最大，端部系數KGibbs和KFu較接近。僅KFu與轉差率相關，其余端部系數均為常數。而采用式(2)中W.J.Gibbs提出的光滑實心轉子端部系數對光滑實心轉子電機進行計算，仿真與實驗結果較吻合[18]。

2 開槽實心轉子端部系數計算

光滑實心轉子的端部系數在轉差率較大時不適用于開槽實心轉子電機[11]。開槽實心轉子中的渦流迫于轉子開槽形狀，在轉子齒上和槽底都有渦流分布。這些沿轉子齒壁分布的渦流增大了轉子渦流通路的面積，且渦流分布將隨轉子開槽數量和轉差率的變化而改變。

文獻[5]依據轉子渦流的等效透入深度修正開槽實心轉子的極距，將開槽實心轉子等效為光滑實心轉子，并計算轉子等效阻抗。但該等效方法假設開槽轉子阻抗角為常數，且等效透入深度的折算與實際情況有較大偏差。本文考慮轉子開槽后渦流沿齒槽分布的規律，計算開槽轉子等效極距，修正常用的式(2)中光滑實心轉子的端部系數KGibbs，得到開槽轉子端部系數Kslit。依舊結合二維有限元仿真計算，可考慮開槽后轉子阻抗角的變化。開槽轉子端部系數Kslit可表示為

(6)

當轉差率較大、渦流等效透入深度小于齒寬度的一半時，轉子渦流沿齒槽分布如圖3所示，齒壁和槽底的渦流呈現波浪形分布，渦流分布面積較光滑轉子有所增大，使開槽轉子的等效極距增大。此時轉子渦流分布示意圖如圖4所示，沿齒壁的渦流厚度從Δ衰減為Δ1，槽底渦流透入深度厚度近似為Δ1。Δ為由光滑轉子計算的透入深度，Δ1可參考文獻[7]，根據有限元計算結果中轉子齒部和轉子槽底磁力線數量的比例估算槽底渦流透入深度Δ1，如式(7)所示。

(7)

圖3 轉差率較大時開槽實心轉子渦流分布Fig.3 Eddy current distribution in slit solid rotor under large slip condition

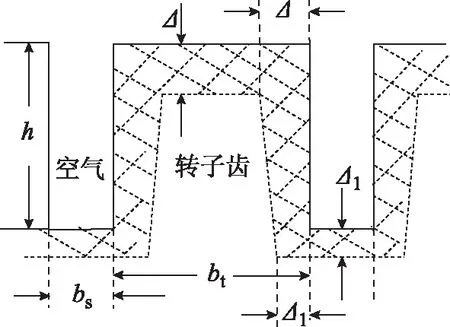
圖4 轉差率較大時開槽實心轉子渦流分布示意圖Fig.4 Schematic diagram of eddy current distribution in slit solid rotor under large slip condition

通常，實心轉子的開槽深度都大于轉子齒寬的一半。假設透入深度層內電流密度均勻分布且相同，將齒壁渦流折算到轉子表面等效透入深度層渦流，從而將轉子極距τ修正為等效極距τ′，如式(8)所示。

τ′=Nslit[bt+bs+(Δ1+Δ)(h-Δ)/Δ]

Δ≤0.5btΔ≤h

(8)

式中，Nslit為轉子每極槽數。

當轉差率較小、渦流等效透入深度大于齒寬度的一半且小于槽深時，轉子渦流在齒部被擠壓到齒底，沿齒槽分布如圖5a所示。此時，轉子渦流分布示意圖如圖6所示，同樣將齒壁渦流折算至轉子表面渦流，得到轉子等效極距τ′的表達式為

τ′=Nslit[bt+bs+(0.5bt+Δ1)(h-Δ)/Δ]

Δ>0.5btΔ≤h

(9)

當轉差率較小、渦流等效透入深度大于齒寬度的一半且大于槽深時，渦流分布形式類似光滑轉子的渦流分布，如圖5b所示。此時，轉子等效極距τ′的表達式為

τ′=Nslit(bt+bs)Δ>0.5btΔ>h

(10)

根據表1中不同槽數的開槽實驗樣機參數，可計算式(6)中不同槽數的開槽轉子端部系數K36slits和K72slits。繪制式(1)～式(5)以及開槽轉子端部系數隨轉差率變化的曲線，如圖7所示。從圖7中可看出開槽轉子端部系數不再是常數，隨轉差率增大而增大。且轉子槽數越多，開槽轉子端部系數增大得越大。

圖5 轉差率較小時開槽實心轉子渦流分布Fig.5 Eddy current distribution in slit solid rotor under small slip condition

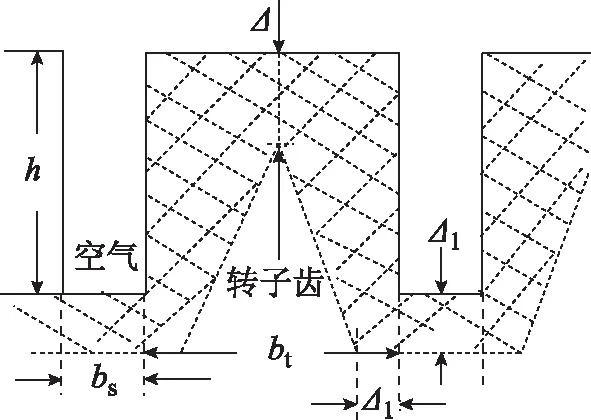
圖6 轉差率較小時開槽實心轉子渦流分布示意圖Fig.6 Schematic diagram of eddy current distribution in slit solid rotor under small slip condition

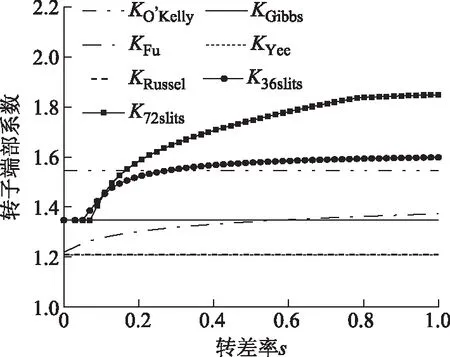
圖7 端部系數隨轉差率變化曲線Fig.7 Rotor end factor curves change with slip

3 仿真與實驗結果比較

實心轉子開槽數量變化將影響轉子渦流分布規律，進而影響轉子等效阻抗。為檢驗第2節中提出的開槽實心轉子端部系數的準確性，本節制造了兩臺定子相同，轉子槽數分別為36和72的開槽實心轉子試驗樣機，其轉子結構如圖8所示，其余主要參數見表1。

圖8 開槽實心轉子Fig.8 Experimental slit solid rotors

有限元軟件和計算機硬件的發展為考慮電機鐵心磁路飽和提供了手段和工具。當考慮開槽實心轉子中的渦流效應時，只能采用諧波場或瞬態場計算。雖然瞬態場計算能更全面地考慮空間諧波磁場，但耗時長，本文采用二維非線性諧波場近似計算。

采用諧波場計算時，定、轉子都靜止。考慮速度效應的二維諧波場無法計算磁路非線性的工況，因此必須對轉子運動進行頻率折算。而開槽實心轉子等效阻抗參數隨著轉差率變化，且與透入深度密切相關。若折算至定子頻率計算，轉子不動，依據轉差率線性修改轉子電阻率，相當于改變了實際的透入深度，即改變了轉子的等效阻抗，與實際不符。

因此，本文采用折算到轉差頻率的非線性諧波場，將輸入電壓以及定子繞組電阻率分別乘以轉差率，避免了由轉差率修改轉子電阻率時引起透入深度的改變。由第2節中提出的開槽轉子端部系數和五個光滑轉子端部系數分別修正轉子電阻率，近似考慮轉子端部效應，計算開槽實心轉子樣機的輸出轉矩。

定子線電壓有效值為220 V和140 V，電壓頻率為50 Hz，在不同轉差率工況下，進行電機負載實驗。對比采用不同端部系數計算36槽實心轉子電機轉矩與實驗測量轉矩，如圖9所示。

在不同工況下，由36槽實心轉子電機計算轉矩的相對誤差取絕對值并做出柱狀圖，如圖10所示。

從圖9和圖10可看出，在轉差率較小時，電機輸出轉矩本身較小，且采用有限元法計算電機轉矩時忽略了電機的機械損耗，因此多數計算轉矩都大于實際測量轉矩。如圖9所示，采用光滑轉子端部系數KGibbs的計算結果在轉差率較小時與實驗較接近，但隨著轉差率增大，其計算結果與實驗結果的絕對誤差增大。從圖10也可看出，采用光滑實心轉子常用的端部系數KGibbs的計算結果在轉差率增大時，其誤差仍大于10%。在轉差率較大時，透入深度效應顯著，轉子開槽對渦流分布影響的作用也更為顯著。而轉差率增大時，采用開槽實心轉子端部系數K36slits的計算結果與實驗結果較吻合。另外，采用光滑轉子端部系數KO′Kelly的計算結果與實驗結果也較為接近。從圖9中也可看到，36槽實心轉子端部系數K36slits隨轉差率增大，且很快趨近于光滑端部系數KO′Kelly。

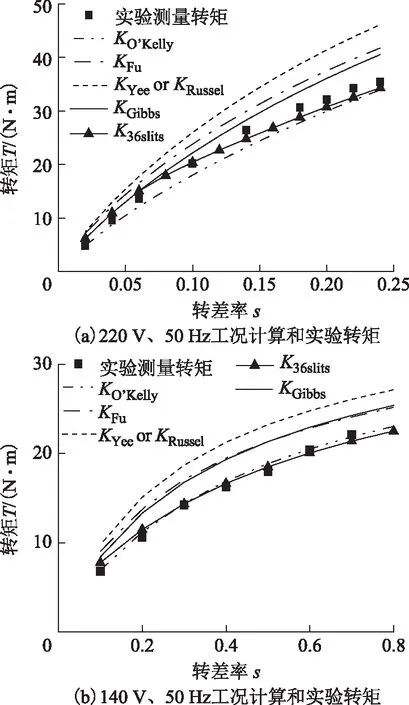
圖9 36槽實心轉子電機不同工況端部系數計算轉矩與實驗轉矩比較Fig.9 Comparison of simulation results and experiment results for slit solid rotor machine with 36 slits under different conditions

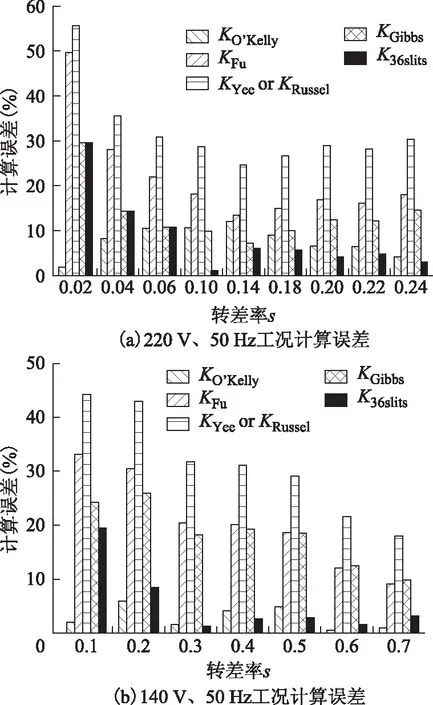
圖10 36槽實心轉子電機不同工況轉矩計算誤差比較Fig.10 Comparison of torque calculation errors for slit solid rotor machine with 36 slits under different conditions

定子線電壓有效值為220 V和140 V，電壓頻率為50 Hz，在不同轉差率工況下，進行電機負載實驗。對比采用不同端部系數計算72槽實心轉子電機轉矩與實驗測量轉矩，如圖11所示。

在不同工況下，根據72槽實心轉子電機計算轉矩的相對誤差取絕對值并做出柱狀圖，如圖12所示。

從圖11和圖12可看出，對于72槽實心轉子電機，采用光滑轉子端部系數計算的電機轉矩與實驗測量轉矩的誤差多在20%以上，甚至更大。如圖12b所示，采用光滑轉子端部系數KO′Kelly計算轉矩的誤差也非常明顯，因此端部系數KO′kelly不再適用于72槽的開槽實心轉子電機。而采用開槽實心轉子端部系數K72slits的計算結果與實驗結果吻合較好，充分說明本文提出的開槽實心轉子端部系數的通用性與有效性。

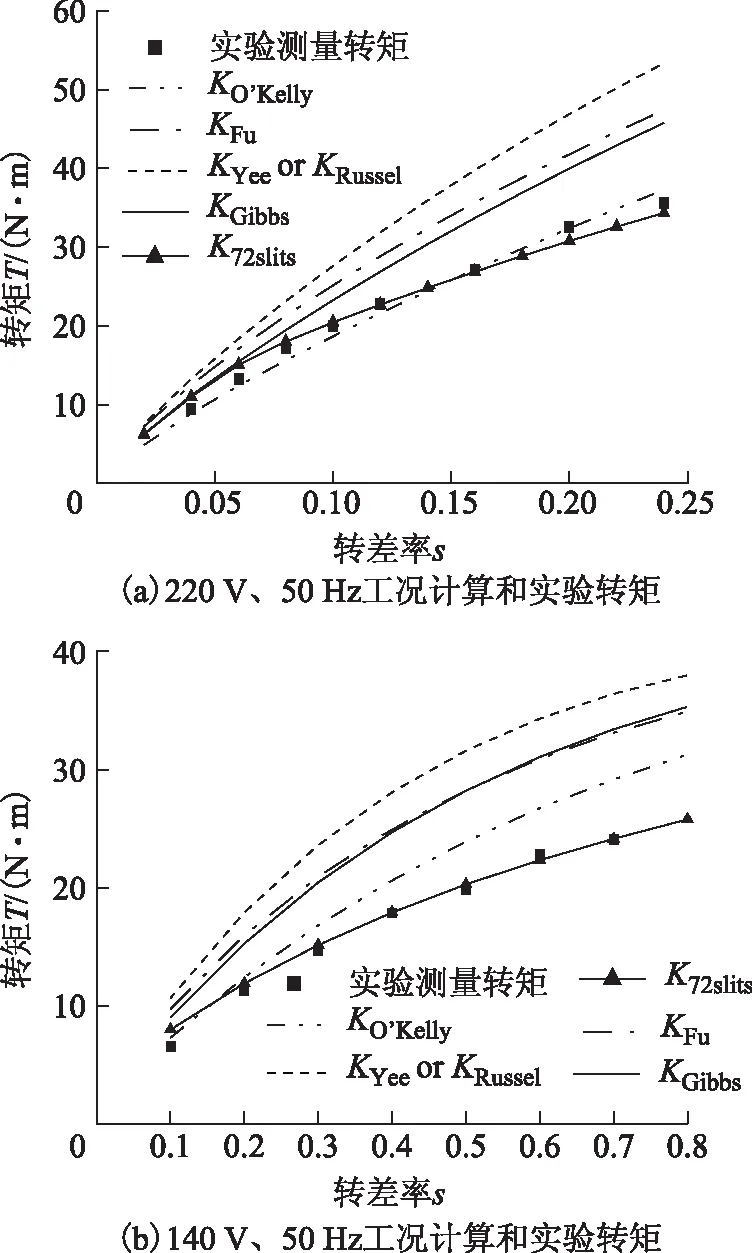
圖11 72槽實心轉子電機不同工況端部系數計算轉矩與實驗轉矩比較Fig.11 Comparison of experiment results and simulation results for slit solid rotor machine with 72 slits under different conditions

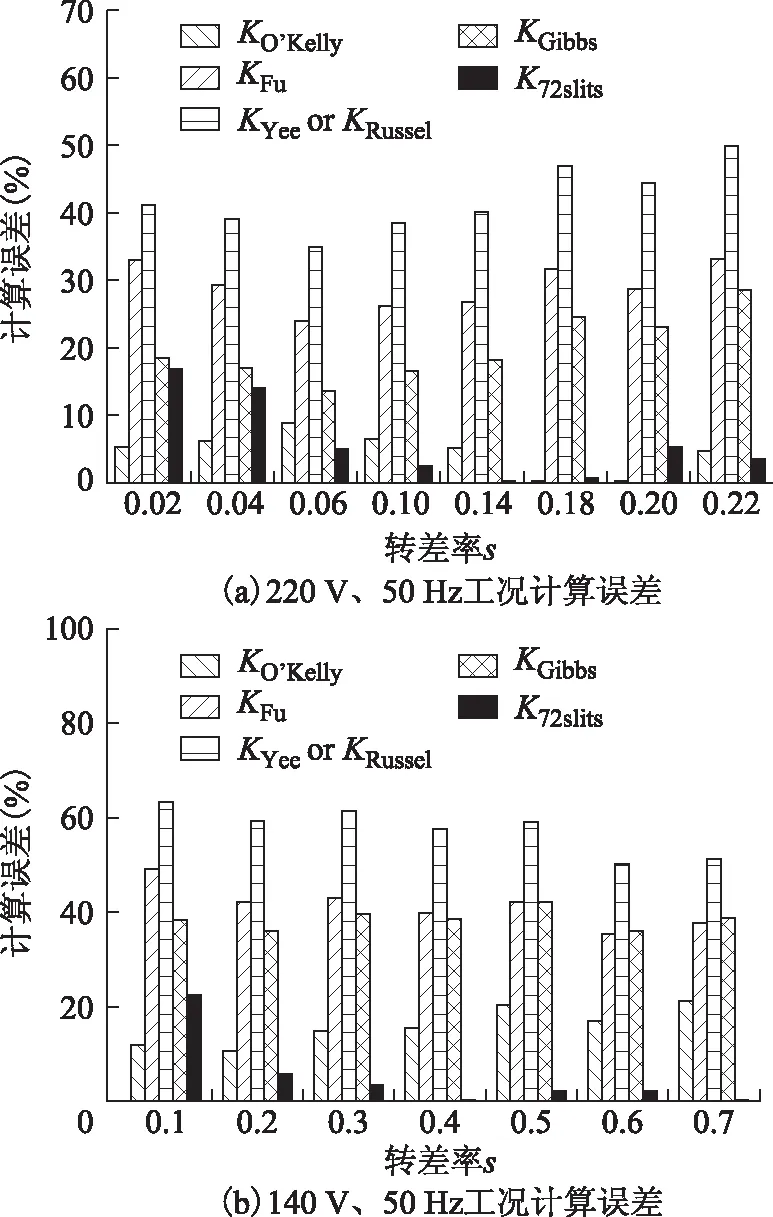
圖12 72槽實心轉子電機不同工況端部系數計算轉矩與實驗轉矩比較Fig.12 Comparison of torque calculation errors for slit solid rotor machine with 72 slits under different conditions

4 結論

本文依據開槽實心轉子渦流分布隨轉差率變化的規律，計算開槽實心轉子等效極距，并提出適用于開槽轉子的端部系數。該開槽實心轉子端部系數隨轉差率增大而增大，且轉子槽數越多，端部系數增大得越多。本文建立了兩臺不同槽數開槽實心轉子樣機的有限元諧波場模型，可考慮定、轉子鐵心磁路飽和。結合現有的不同光滑轉子端部系數和提出的開槽轉子端部系數修正轉子電阻率，近似考慮轉子端部效應的作用。在不同工況下，比較了實驗樣機轉矩的仿真計算和實驗結果，說明了現有的光滑實心轉子端部系數不適用于開槽實心轉子電機，尤其在轉差率較大工況下。驗證了本文提出的開槽實心轉子端部系數在全轉差率范圍的有效性，可以用于開槽實心轉子電機的參數計算與優化設計。

[1] Gerada D，Mebarki A，Brown N L，et al.High-speed electrical machines：technologies，trends，and developments[J].IEEE Transactions on Industrial Electronics，2014，61(6)：2946-2959.

[2] 張鳳閣，杜光輝，王天煜，等.高速電機發展與設計綜述[J].電工技術學報，2016，31(7)：1-18. Zhang Fengge，Du Guanghui，Wang Tianyu，et al.Review on development and design of high speed machines[J].Transactions of China Electrotechnical Society，2016，31(7)：1-18.

[3] Arkkio A，Jokinen T，Lantto E.Induction and permanent-magnet synchronous machines for high-speed applications[C]//Proceedings of the Eighth International Conference on Electrical Machines and Systems，2005，2：871-876.

[4] Pyrhonen J，Nerg J，Kurronen P，et al.High-speed high-output solid-rotor induction-motor technology for gas compression[J].IEEE Transactions on Industrial Electr-onics，2010，57(1)：272-280.

[5] 馮爾健.鐵磁體實心轉子異步電機理論與計算[M].北京：科學出版社，1980.

[6] Aho T，Nerg J，Pyrhonen J.The effect of the number of rotor slits on the performance characteristics of medium-speed solid rotor induction motor[C]//The 3rd IET International Conference on Power Electronics，Machines and Drives，2006：515-519.

[7] 唐孝鎬.實心轉子異步電機及其應用[M].北京：機械工業出版社，1991.

[8] Dorairaj K R，Krishnamurthy M R.Polyphase induction machine with a slitted ferromagnetic rotor：II-analysis[J].IEEE Transactions on Power Apparatus & Systems，1967，PAS-86(7)：844-855.

[9] Zaim M E.Non-linear models for the design of solid rotor induction machines[J].IEEE Transactions on Magnetics，1999，35(3)：1310-1313.

[10]Gessese Y，Binder A.Axially slitted，high-speed solid-rotor induction motor technology with copper end-rings[C]//International Conference on Electrical Machines and Systems，2009：1-6.

[11]Jagiela M，Garbiec T.Evaluation of rotor-end factors in solid-rotor induction motors[J].IEEE Transactions on Magnetics，2012，48(1)：137-142.

[12]O′Kelly D.Theory and performance of solid-rotor induction and hysteresis machines[J].Proceedings of the Institution of Electrical Engineers，1976，123(5)：421-428.

[13]Gibbs W J.Induction and synchronous motors with unlaminated rotors[J].Journal of the Institution of Electrical Engineers-Part II：Power Engineering，1948，95(46)：411-420.

[14]Russel R L，Norsworthy K H.Eddy currents and wall losses in screened-rotor induction motors[J].Procee-dings of the IEE-Part A：Power Engineering，1958，105(20)：163-175.

[15]Yee H.Effects of finite length in solid-rotor induction machines[J].Proceedings of the Institution of Electrical Engineers，1971，118(8)：1025-1033.

[16]傅豐禮.異步電動機設計手冊[M].北京:機械工業出版社，2002.

[17]兵器工業無損檢測人員技術資格鑒定考核委員會.常用鋼材磁特性曲線速查手冊[M].北京:機械工業出版社，2003.

[18]黃子果，王善銘，倪守輝.光滑實心轉子異步電機等效電路參數的二維計算方法[J].中國電機工程學報，2016，36(9)：2505-2512. Huang Ziguo，Wang Shanming，Ni Shouhui.2D calcul-ation methods of equivalent-circuit parameters in smooth solid rotor induction machines[J].Proceedings of the CSEE，2016，36(9):2505-2512.

(編輯 于玲玲)

Calculation and Comparison of Rotor End Factors of Solid Rotor Induction Machines with Axial Slits

HuangZiguo1WangShanming1SunYuguang1CaoHaixiang1YangZhanlu1，2

(1.State Key Laboratory of Control and Simulation of Power System and Generation Equipments Department of Electrical Engineering Tsinghua University Beijing 100084 China 2.Navy Submarine Academy Qingdao 266100 China)

When the nonlinearity of rotor magnetic circuit is taken into account，the huge computation of 3D finite element calculation of slitted solid rotor magnetic field is unavoidable.To simplify the calculation，the 2D FEM combined with end factors of smooth solid rotor is adopted generally.However，the calculation error increases along with the increase of slip when applying end factors of smooth solid rotor for the slitted rotor.This paper puts forward a new rotor end factor for slitted solid rotor using an approximate calculation method due to the eddy current distribution in the slitted rotor.With the 2D FEM and the raised end factor，the effect of saturation in both stator and rotor core and the axial finite length of rotor are taken into account.The calculation results using different smooth rotor end factors and the raised slitted rotor end factor are compared with each other.And the simulation results using slitted rotor end factor agree well with the experimental test results on model machines with different number of rotor slitted.This indicates the raised slitted rotor end factor is suitable for the parameter calculation and optimal design of slitted solid-rotor induction machine.

Slitted solid rotor，rotor end factor，2D FEM

國家自然科學基金項目(51177077)和國家科技支撐計劃項目(2014BAA04B02)資助。

2016-08-19 改稿日期2016-12-21

10.19595/j.cnki.1000-6753.tces.L70314

TM346

黃子果 男，1990年生，博士研究生，研究方向為實心轉子電機設計和多相電機內部短路故障分析。

E-mail：huangzg.2007@163.com(通信作者)

王善銘 男，1972年生，副教授，研究方向為特殊電機設計分析、發電機內部故障分析和電機電磁場分析。

E-mail：wangsm96@mails.tsinghua.edu.cn