一種基于灰預測理論的混合蛙跳算法
杜 江 袁中華 王景芹
(河北工業大學電磁場與電器可靠性省部共建重點實驗室 天津 300130)
一種基于灰預測理論的混合蛙跳算法
杜 江 袁中華 王景芹
(河北工業大學電磁場與電器可靠性省部共建重點實驗室 天津 300130)
為提高混合蛙跳算法在優化問題求解中的性能,提出一種基于灰預測理論的改進混合蛙跳算法。該算法首先將基本算法的進化模式進行調整,強化了進化過程中全局信息的交換;之后引入移動步長變異算子,根據進化過程的不同階段和利用灰預測理論獲得進化過程中最優解進步速度,并借鑒模糊控制思想對該變異算子進行控制,進而實現移動步長的自適應調整。采用6個標準測試函數,與基本算法和已有改進算法進行性能對比分析,證明了改進后的混合蛙跳算法在收斂精度、收斂速度和收斂成功率方面的優越性及灰預測理論在算法改進領域中的可行性。最后,將改進算法應用于10 kV油浸式配電變壓器優化設計工作中,驗證了該改進算法的實用性。
混合蛙跳算法 灰預測 變異算子 優化設計
0 引言
近年來,應優化問題之需求,各種智能仿生算法相繼被提出,如遺傳算法、粒子群算法、混合蛙跳算法(Shuffled Frog Leaping Algorithm,SFLA)等。其中,混合蛙跳算法于2003年由M.M.Eusuff等[1]提出,該算法是結合了模因算法和粒子群優化算法的一種全新智能仿生算法,具有結構簡單、設置參數數量較少、魯棒性強等優點,一經提出便在計算機領域和許多工程領域得到了廣泛的應用[2-6]。
然而,混合蛙跳算法也存在易陷入局部最優、收斂精度不高和收斂成功率低等不足。為了提高該算法的整體性能,國內外學者進行了大量的研究與改進。文獻[7]將變異算子引入算法,加強了青蛙種群的多樣性,增加了解空間的搜索范圍,降低了算法早熟的可能性。文獻[8]把加速因子的概念引入子種群內部迭代中,提高了算法整體尋優能力。文獻[9]將差分進化機制有機地嵌入進化過程中,改善了種群的多樣性,進而提高了算法在復雜優化問題中的尋優能力。
本文針對基本混合蛙跳算法的不足,將算法的運行模式予以調整,并引入移動步長變異算子和灰預測理論,進而構建一種基于灰預測理論的新模式混合蛙跳算法(New Model for Shuffled Frog Leaping Algorithm,PMSFLA)。仿真結果表明,改進后的算法在收斂精度、收斂速度、收斂成功率以及實用性方面都具有較好的效果,算法的綜合性能得到了有效提升。
1 基本混合蛙跳算法
基本混合蛙跳算法是一種全局尋優的啟發式智能仿生算法,其尋優過程是模擬自然界中青蛙撲食現象。該算法每次進化過程可分為兩大機制:種群混合排序機制和子種群內部尋優機制。種群混合排序機制,即種群中青蛙個體按照適應度進行排序、重新劃分子種群。子種群內部尋優機制,即子種群內部進化。
設蛙群由F個分布在D維解空間的青蛙個體組成,每個子種群中參與進化青蛙個體的屬性均含有兩個D維矢量:Xi=(xi1,xi2,…,xiD)和Di=(di1,di2,…,diD),其中,1≤i≤m,-Dimax≤Di≤Dimax,Dimax為最大移動步長。進化式為
Di=rand( )×(Xi-Xw)
(1)
Xw(new)=Xw(old)+Di
(2)
Xw(new)=Xw(old)+rand( )×Dimax
(3)
式中,Di為移動步長;rand()表示取(0,1)區間的隨機數;Xw(old)、Xw(new)分別為進化前、后的青蛙個體位置。當式(2)為局部深度搜索時,Xi為子種群最優個體位置Xb;當式(2)為全局深度搜索時,Xi為整個種群最優個體位置Xg,式(3)為隨機移動公式。
算法根據適應度判斷其位置的優劣,每次進化均是由子種群的最差個體參與,且每次進化選擇進行局部深度搜索、全局深度搜索和隨機移動三種操作中的一種。
2 改進的混合蛙跳算法
2.1 算法模式的調整
基本混合蛙跳算法中,青蛙種群按照適應度排序、劃分子種群之后,每個子種群各自進行內部進化,直到達到內部進化次數或滿足其他結束條件。之后,判斷是否滿足整個算法的結束條件,如果滿足則結束,否則再次進行排序、劃分子種群、子種群內部進化,直到滿足整個算法的結束條件。此進化過程的不足之處是:子種群內部的多次進化中,由于子種群進化間不平衡性的存在,不能保證每次進化均是以種群適應度最優的前m個個體為進化目標。
鑒于基本混合蛙跳算法的上述問題,本文對基本算法的進化模式予以調整:將基本混合蛙跳算法中的種群混合排序(劃分子種群)機制與子種群內部進化機制進行合并處理,即子種群內部每進行一次進化就進行一次種群混合排序(劃分子種群)。這種每次進化前都進行混合排序(劃分子種群)操作的運行模式打破了子種群對青蛙個體進化的限制,提高了局部深度搜索中進化目標的質量,即保證了子種群每次局部深度搜索的進化目標都是全種群最優秀的m個個體之一。如此調整之后構成的新模式混合蛙跳算法,加強了算法全局信息的交換,簡化了算法的進化模式,對算法跳出局部極值點、提高進化效率有很大幫助。
2.2 自適應步長思想的引入
在算法進化過程中,采用合適的移動步長,可同時兼顧算法的收斂速度和收斂精度。所以,本文引入移動步長變異算子,自適應調整移動步長的大小。
2.2.1 變異算子的引入
遺傳算法是一種經典的現代優化算法,廣泛應用于工程領域中[10,11]。本文效仿遺傳算法,添加變異操作機制,自適應地改變移動步長(移動速度)的大小,是一種非常有效的提高求解性能的方法。本文在種群進化的移動步長中,引入變異算子將式(1)改進為[7]
Di=rand( )×bi(Xi-Xw)
(4)
式中,bi為移動步長的變異算子。
由式(4)可看出,變異算子的大小直接影響移動步長的大小,進而影響蛙群對解空間的搜索范圍。顯然,bi取值較大時的移動步長較大,所搜索的解空間范圍就較大;反之,搜索空間較小。當算法處于進化前期,較大的移動步長可以提高算法收斂速度,使蛙群迅速聚集在最優解附近;當算法處于進化后期,較小的移動步長可以減緩粒子在最優解附近的往復振蕩,使算法更精確地收斂于最優解。另外,當算法具有較快的進步速度時,較小的移動步長可較大可能地避免粒子跳過解空間內較優的位置;當算法的進步速度較慢時,說明算法很有可能陷入局部最優,此時較大的移動步長有助于算法跳出局部最優。
通過上述分析,本文最終確定了移動步長的變異算子bi的控制量:“算法進化階段”和“算法進步速度”。即這兩個控制量共同決定bi的取值。
2.2.2 灰預測控制器設計
灰預測控制器設計如圖1所示,其中S和V為變異系數控制器的輸入量,分別表示“算法進化階段”和“算法進步速度”兩個控制量的測量值。由這兩個控制量的測量值,通過控制規則共同決定變異算子bi的取值。

圖1 灰預測控制器設計Fig.1 Grey prediction controller design

2)算法進步速度測量值V。設Yg1、Yg2分別表示相鄰兩次進化種群最優適應度,用它們的差值Yg2-Yg1表示算法當前的進步速度。設vmark_min、vmark_max分別表示算法進步速度的閾值,當Yg2-Yg1∈(-∞,vmark_min]時,則認為算法進步速度較小,說明很可能收斂于局部最優解附近,此時應使bi取一較大值,這樣有助于算法跳出局部最優解;當Yg2-Yg1∈[vmark_max,+∞)時,則認為算法進步速度較大,此時應使bi取一較小值,避免移動步長太大而漏掉解空間內較好的解;當Yg2-Yg1∈(vmark_min,max),即進步速度適中時,bi取一適中值。
傳統方法是得到Yg1之后,再進行一次算法進化得到Yg2,進而作差由Yg2-Yg1判斷算法的進步速度。然而這種獲取算法進步速度的方法具有明顯的滯后性:若進步速度顯示需要調整bi,則相當于為了調整bi進行了一次質量很差的進化。針對此問題,本文獲取進步速度的方式不是進行下一次的實際進化,而是根據已有數據對下一次進化結果進行預測,根據預測結果求得當前進步速度,進而調整變異算子bi的取值。這種“防患于未然”的控制思想,大大減少了徒勞的進化代數,對減小算法運行的盲目性、提高運行效率具有顯著效果。
灰預測理論[12]是灰理論的一部分,具有所需原始數據少、環境適應性強、預測精度高等優點且計算量較小,因此本文采用灰預測理論對下一次進化結果進行預測。
結合變異算子的控制特點,對灰預測過程闡述如下。
(1)設置原始序列:x=(x(1),x(2),…,x(p)),其中p≥4,x(1),x(2),…,x(p)是最近的連續p次進化的種群最優適應度。x(1),x(2),…,x(p)是一組遞增的序列。
(2)級比平滑檢驗:利用式(5)進行級比平滑檢驗。
(5)

(3)白化型GM(1,1)建模。
①利用式(6)進行AGO處理。
x(1)(q)=x(1)(q-1)+x(q) 1≤q≤p
(6)
且當q=1時,x(1)(1)=x(1)。
②利用式(7)進行MEAN處理。
z(1)(q)=0.5x(1)(q)+0.5x(1)(q-1) 2≤q≤p
(7)
③利用式(8)和式(9)求得發展系數a和灰作用量b。
(8)
(9)
④利用式(10)和式(11)求得GM(1,1)白化響應式。
(10)
(11)
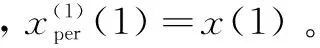
(4)殘差檢驗:利用式(10)~式(12)求得殘差序列e(1),e(1),…,e(p),進而利用式(13)求得精度p。。
(12)
(13)
式中,e(1)=0。若p。<90%,說明原始數列的波動性較大,即算法具有較快的進步速度,則給變異算子bi賦一較小值,灰預測過程到此結束;否則說明此方法具有較高的預測精度,進而繼續步驟(5)。
(5)利用式(14)預測下一次迭代后的最優適應度。
(14)
如果Yg_per-Yg較小,說明算法進步速度較慢,則給變異算子bi賦一較大值;否則給變異系數bi賦一較小值。
3)當這兩個控制量的“意見”出現分歧時,應綜合考慮其對算法的影響,決定給變異算子bi賦以較大值bib、適中值bim還是較小值bil。綜上分析,并借助模糊控制的思想,得到變異算子控制規則見表1。

表1 控制規則Tab.1 Control rules table
2.3 改進后算法流程
將基本混合蛙跳算法改進后,得到一種基于灰預測理論的新模式混合蛙跳算法,算法流程如下:
1)對算法參數及蛙群進行初始化。
2)計算每只青蛙個體的適應度Yi。
3)對該蛙群按適應度從優到差進行降優排序。
4)將該青蛙種群分為m個青蛙子種群,具體劃分子種群方法描述如下:蛙群按適應度從優到差排序,第1只青蛙分給第1子種群,第2只青蛙分給第2子種群,…,第m只青蛙分給第m子種群,第m+1只青蛙分給第1子種群,第m+2只青蛙分給第2子種群,…,第F只青蛙分給第m子種群。
5)找出每個子種群中適應度最優的青蛙位置Xb和適應度最差的青蛙位置Xw。
6)對每個子種群中適應度最差的青蛙進行更新處理。對其執行的操作進行選擇,包括局部深度搜索、全局深度搜索和隨機移動。各操作描述如下:①首先試探局部深度搜索,利用式(2)和式(4)使子種群適應度最差個體向子種群適應度最優個體方向前進一步,如果Xw(new)的適應度優于Xw(old)的適應度,則確定執行局部深度搜索并跳轉至步驟7,否則拋棄局部深度搜索;②試探全局深度搜索:利用式(2)和式(4)使子種群適應度最差個體向種群適應度最優個體方向前進一步,如果Xw(new)的適應度優于Xw(old)的適應度,則確定執行全局深度搜索并跳轉至步驟7,否則拋棄全局深度搜索;③利用式(3)執行隨機移動。
7)計算更新后每只青蛙的適應度Yi,并找出種群最優適應度Yg及其位置Xg。
8)如果算法當前進化代數i 9)判斷是否滿足結束條件,即判斷是否達到最大混合迭代次數N1或滿足最小允許誤差Δ。如果不滿足結束條件,則執行步驟3;否則輸出優化結果并結束。 3.1 變異參數的確定 通過前文的分析可知,變異參數bil、bim、bib的不同取值對PMSFLA的綜合性能有較大影響。若bil、bim、bib的取值分別在0.6~0.8、0.9~1.1、1.8~2.2之間,則PMSFLA的性能較好。本文通過實驗法確定能夠使PMSFLA展現出優秀性能的變異參數的最佳組合。表2給出了不同變異參數組合下算法PMSFLA對測試函數Schwefel的仿真結果,函數信息見表3。其中,PMSFLA的青蛙個體數F=48,子種群數m=8,最大移動步長Djmax=0.3,最大混合迭代次數N1=100,子種群內部迭代次數N2=20,各控制參數pmark_min=0.5、pmark_max=0.75、vmark_min=0.05、vmark_max=0.5。表2中平均收斂精度為PMSFLA在10維度解空間內運行20次的平均收斂精度;收斂次數為算法PMSFLA在10維度解空間內運行20次中收斂精度達到10-20的次數,每次運行的最大混合迭代次數為100次。 表2 Schwefel函數測試結果Tab.2 The test results of Schwefel function 由表2可看出,變異參數bib=2、bim=1、bil=0.8的組合可認為是使PMSFLA展現非常優異的綜合性能的最佳組合,因此,下文的仿真也將采用該參數組合。 3.2 實驗設計 為了檢驗本文改進基本混合蛙跳算法思路的可行性,將MSFLA和PMSFLA與基本SFLA和葛等宇[7]提出的改進算法(ImprovedShuffledFrogLeapingAlgorithm,ISFLA)做對比實驗。實驗選擇6個典型的測試函數進行性能測試[13],該6個測試函數的名稱、表達式等信息見表3。 實驗的硬件環境為:WindowsXP系統,AMD雙核2.5GHzCPU,1.94G內存。通過VC++軟件編寫程序進行仿真實驗。算法MSFLA、PMSFLA、SFLA和ISFLA的參數設置如下:青蛙個體數F=48,子種群數m=8,最大移動步長Djmax=0.3,最大混合迭代次數N1=200,子種群內部迭代次數N2=20,各控制參數pmark_min=0.5、pmark_max=0.75、vmark_min=0.05、vmark_max=0.5、bib=2、bim=1、bil=0.8。本文實驗從四個方面進行驗證。 表3 測試函數信息Tab.3 Test function information 1)固定算法進化代數,根據多次實驗的平均最優解比較四種算法的求解精度。 2)固定算法進化代數,通過記錄多次實驗的運行時間比較四種算法求解的計算量。 3)通過多次實驗的平均進化曲線比較四種算法的收斂速度。 4)固定收斂精度,結合進化代數比較四種算法收斂的成功率。 3.3 實驗結果及分析 3.3.1 算法求解精度對比 每種算法對每個測試函數在不同維度下均進行20次實驗,表4給出了該20次實驗的平均最優解。 由表4可看出,相對于SFLA,MSFLA在大多數優化問題下都具有更高的求解精度;相對于另外兩種算法,PMSFLA在不同優化問題下的求解精度均優于其他三種算法。另外,PMSFLA與MSFLA的對比,體現了自適應移動步長思想在求解精度方面的貢獻。此外由表4還可看出,由于不同測試函數在解空間內的分布特性各異,PMSFLA對不同測試函數在其收斂精度方面的提高有著相對明顯的差異,對函數f2和函數f6收斂精度的提高比較有限。 表4 各函數在不同算法不同維度下的平均最優解Tab.4 The average optimum solution of each function in the different algorithms under the different dimensions 3.3.2 算法求解計算量對比 設定解空間維度D=10。每種算法對每個測試函數進行20次實驗,每次實驗進行200次混合迭代,記錄該20次實驗的總計算時間之和,見表5。 表5 各函數在不同算法下的運行時間Tab.5 The runtime of each function in the different algorithms 表5中,SFLA與MSFLA的運行時間對比顯示了對算法進化模式的調整,使算法進行混合迭代時計算量的增加;MSFLA與PMSFLA的運行時間對比顯示了對算法移動步長的調整,使算法進行混合迭代時計算量的增加。總體來講,MSFLA和PMSFLA的運行時間略長于SFLA,而與ISFLA的運行時間基本相當,說明MSFLA和PMSFLA在計算復雜度方面的增加非常有限。 3.3.3 算法收斂速度對比 設定解空間維度D=10。每種算法對每個測試函數進行20次實驗,得到200次混合迭代中每一代的平均最優解數據,繪制收斂曲線,如圖2所示。同時為了較直觀地展示各算法的進化趨勢,對其進化數據取自然對數。圖2中函數f3的收斂曲線中SFLA與MSFLA兩條曲線幾乎重合。 圖2 各測試函數收斂曲線Fig.2 Evolution curves of each test function 由圖2可知,MSFLA在大多數優化問題下的收斂速度都優于SFLA;PMSFLA在函數f1下的收斂速度與SFLA和MSFLA相仿、比ISFLA較差,在其他函數下的收斂速度均優于其他三種算法。另外,圖2中PMSFLA與MSFLA的收斂曲線對比,說明合理地移動步長能夠更快地尋得更優解。 3.3.4 算法收斂成功率對比 設定各測試函數的收斂精度見表6,解空間維度D=10。每種算法對每個測試函數進行50次實驗,混合迭代次數達到200次時仍未達到指定收斂精度,則認為此次實驗沒有收斂。記錄收斂時算法進行混合迭代的次數、收斂成功次數,并計算收斂成功率見表7,其中,收斂成功率=收斂成功次數/50。 表6 各測試函數收斂精度Tab.6 The convergence precision of each test function 表7 各測試函數收斂成功率Tab.7 Success rate of convergence of each test function 由表7可知,對于以上6個測試函數,相對于SFLA,MSFLA在部分優化問題下的收斂成功率有所提高;PMSFLA的收斂成功率均高于其他三種算法。 綜上分析,本文提出的PMSFLA在收斂精度、收斂速度和收斂成功率方面都得到了滿意的效果,體現了PMSFLA的優越性。 近年來,越來越多的智能優化算法被用于解決電力系統領域的優化問題[14-17]。為了檢驗本文提出的PMSFLA的實用性,將該改進算法應用于10 kV級容量為200 kV·A 的油浸式配電變壓器優化設計中,并將其優化結果與窮舉法和某廠家人工設計結果作對比。 實驗的硬件環境為:Windows XP系統,AMD雙核2.5 GHz CPU,1.94 G內存。PMSFLA參數設置:青蛙種群中青蛙個體數F=20,子種群數m=5,每個子種群內青蛙個體數n=4,最大移動步長Djmax=0.3,算法進化代數N1=20,子種群內部搜索次數N2=8,pmark_min=0.5,pmark_max=0.75,vmark_min=0.05,vmark_max=0.5,bib=2,bim=1,bil=0.8。 表8為不同優化方式下以變壓器總成本為目標函數,以鐵心直徑、低壓線圈匝數、低壓導線規格和高壓導線規格為變量的優化結果。其中,變壓器總成本=制造成本+10年運行成本。從目標函數上看,PMSFLA的優化結果比人工設計結果節省1.21%的總成本,比窮舉法獲得的優化結果總成本只高0.12%。而從計算時間上看,窮舉法耗時38.35 min,而PMSFLA耗時為3.45 min,耗費時間比為11.12倍。綜上所述,PMSFLA進行變壓器優化設計具有很大的優勢,PMSFLA具有很強的工程實用性。 表8 10 kV油浸式配電變壓器優化結果Tab.8 Optimization results of 10 kV oil-immersed distribution transformer 本文對基本SFLA進行改進:調整算法的運行模式,將基本混合蛙跳算法中的種群混合排序(劃分子種群)機制與子種群內部進化機制進行合并處理;引入移動步長變異算子,并采用灰預測方式獲取最優解進步速度,實現了移動步長的動態調整。仿真實驗結果表明:本文提出的改進混合蛙跳算法有效提高了算法的求解精度、收斂速度和收斂成功率,增強了算法的尋優性能。本文采用的預測思想不僅適用于改進混合蛙跳算法,也可應用于其他優化算法的改進工作。最后通過將本文提出的PMSFLA應用于10 kV油浸式配電變壓器優化設計工作中,證明了該改進算法的實用性和優越性。 [1] Eusuff M M,Lansey K E.Optimization of water distribution network design using the shuffled frog leaping algorithm[J].Water Resour Plan Manage,2003,129(3):210-225. [2] 代永強,王聯國,施秋紅,等.改進的混合蛙跳算法性能分析及其在電力系統經濟調度中的應用[J].電力系統保護與控制,2012,40(10):77-83. Dai Yongqiang,Wang Lianguo,Shi Qiuhong,et al.Performance analysis of improved SFLA and the application in economic dispatch of power system[J].Power System Protection and Control,2012,40(10):77-83. [3] 耿超,王豐華,蘇磊,等.基于人工魚群與蛙跳混合算法的變壓器Jiles-Atherton模型參數辨識[J].中國電機工程學報,2015,35(18):4799-4807. Geng Chao,Wang Fenghua,Su Lei,et al.Parameter identification of Jiles-Atherton model for transformer based on hybrid artificial fish swarm and shuffled frog leaping algorithm[J].Proceedings of the CSEE,2015,35(18):4799-4807. [4] 王茜,張粒子,舒雋,等.基于閾值選擇策略的改進混合蛙跳算法在電網規劃中的應用[J].電力系統保護與控制,2011,39(3):34-39. Wang Qian,Zhang Lizi,Shu Jun,et al.Application of improved shuffled frog leaping algorithm based on threshold selection strategy in transmission network planning[J].Power System Protection and Control,2011,39(3):34-39. [5] 張沈習,陳楷,龍禹,等.基于混合蛙跳算法的分布式風電源規劃[J].電力系統自動化,2013,37(13):76-82. Zhang Shenxi,Chen Kai,Long Yu,et al.Distributed wind power planning based on hybrid leapfrog algorithm[J].Automation of Electric Power Systems,2013,37(13):76-82. [6] 王介生,高憲文.基于改進蛙跳算法的電渣重熔過程多變量PID控制器設計[J].控制與決策,2011,26(11):1731-1734. Wang Jiesheng,Gao Xianwen.Design of multivariable PID controller of electroslag remelting process based on improved shuffled frog leaping algorithm[J].Control and Decision,2011,26(11):1731-1734. [7] 葛宇,王學平,梁靜.改進的混合蛙跳算法[J].計算機應用,2012,32(1):234-237. Ge Yu,Wang Xueping,Liang Jing.Improved shuffled frog leaping algorithm[J].Journal of Computer Applications,2012,32(1):234-237. [8] Elbeltagi E,Hegazy T,Grierson D.A modified shuffled frog-leaping optimization algorithm application to project management[J].Structure and Infrastructure Engineering,2007,3(1):53-60. [9] 趙鵬軍,邵澤軍.一種新的改進的混合蛙跳算法[J].計算機工程與應用,2012,48(8):48-50. Zhao Pengjun,Shao Zejun.Novel improved shuffled frog leaping algorithm[J].Computer Engineering and Applications,2012,48(8):48-50. [10]肖曦,許青松,王雅婷,等.基于遺傳算法的內埋式永磁同步電機參數辨識方法[J].電工技術學報,2014,29(3):21-26. Xiao Xi,Xu Qingsong,Wang Yating,et al.Parameter identification of interior permanent magnet synchronous motors based on genetic algorithm[J].Transactions of China Electrotechnical Society,2014,29(3):21-26. [11]鄧軍,郝艷捧,李立浧,等.復雜導線垂直斷面地勢下直流線路無線電干擾計算的信賴域正則化遺傳算法[J].電工技術學報,2014,29(10):304-311. Deng Jun,Hao Yanpeng,Li Licheng,et al.Trust region regularization genetic algorithm for radio interference of DC transmission lines passing through complex vertical section terrains of conductors[J].Transactions of China Electrotechnical Society,2014,29(10):304-311. [12]鄧聚龍.灰預測與灰決策[M].武漢:華中科技大學出版社,2002. [13]陶新民,劉福榮,劉玉,等.定向多尺度變異克隆選擇優化算法[J].控制與決策,2011,26(2):175-181. Tao Xinmin,Liu Furong,Liu Yu,et al.Clone selection optimization algorithm with directional multi-scale mutation[J].Control and Decision,2011,26(11):175-181. [14]劉華臣,王錫淮,肖健梅,等.基于群搜索算法的電力系統無功優化[J].電力系統保護與控制,2014,42(14):93-99. Liu Huachen,Wang Xihuai,Xiao Jianmei,et al.Reactive power optimization based on group search optimizer[J].Power System Protection and Control,2014,42(14):93-99. [15]周超,田立軍.基于粒子群優化算法的電壓暫降監測點優化配置[J].電工技術學報,2014,29(4):181-187. Zhou Chao,Tian Lijun.An optimum allocation method of voltage sag monitoring nodes based on particle swarm optimization algorithm[J].Transactions of China Electrotechnical Society,2014,29(4):181-187. [16]宮金林,王秀和.基于多目標有效全局優化算法的直線感應電動機優化設計[J].電工技術學報,2015,30(24):32-37. Gong Jinlin,Wang Xiuhe.Optimal design of a linear induction motor using multi-objective efficient global optimization[J].Transactions of China Electrotechnical Society,2015,30(24):32-37. [17]程聲烽,程小華,楊露.基于改進粒子群算法的小波神經網絡在變壓器故障診斷中的應用[J].電力系統保護與控制,2014,42(19):37-42. Cheng Shengfeng,Cheng Xiaohua,Yang Lu.Application of wavelet neural network with improved particle swarm optimization algorithm in power transformer fault diagnosis[J].Power System Protection and Control,2014,42(19):37-42. (編輯 張洪霞) Shuffled Frog Leaping Algorithm Based on Grey Prediction Theory DuJiangYuanZhonghuaWangJingqin (Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China) To enhance the performance of shuffled frog leaping algorithm in solving optimization problems,a new model for hybrid leapfrog algorithm based on grey prediction theory was proposed.The algorithmic evolution model was adjusted to strengthen the ability to exchange the global information in the process of evolution.Then the algorithm implemented the mobile step self-adaption adjustment through introduced mobile step mutation operator.The mutation operator was controlled by the different stages of evolution and the optimal solution progress speed in the process of evolution obtained by grey prediction theory and the fuzzy control thoughts.The advantages of the improved hybrid leapfrog algorithm,such as the accuracy,convergent speed and success rate,and the feasibility of grey prediction theory in the field of algorithm improvement,is verified by comparison with the basic shuffled frog leaping algorithm and the known improved algorithm on performance through six standard test functions.Finally,the practicability of the improved algorithm is proved by applying it to 10 kV oil-immersed distribution transformer optimization design works. Shuffled frog leaping algorithm,grey prediction,mutation operator,optimal design 2016-05-09 改稿日期2016-08-26 10.19595/j.cnki.1000-6753.tces.160634 TP301 杜 江 男,1972年生,博士,副教授,研究方向為變壓器優化設計和現代智能仿生算法及其應用。 E-mail:dj@hebut.edu.cn 袁中華 男,1991年生,碩士研究生,研究方向為變壓器優化設計和現代智能仿生算法及其應用。 E-mail:1003816201@qq.com(通信作者) 河北省自然科學基金(E2016202134)、河北省人社廳項目(A2013007001)、河北省科學技術研究與發展項目(13210129)和河北省高等學校創新團隊領軍人才培育計劃項目(LJRC003)資助。3 仿真實驗
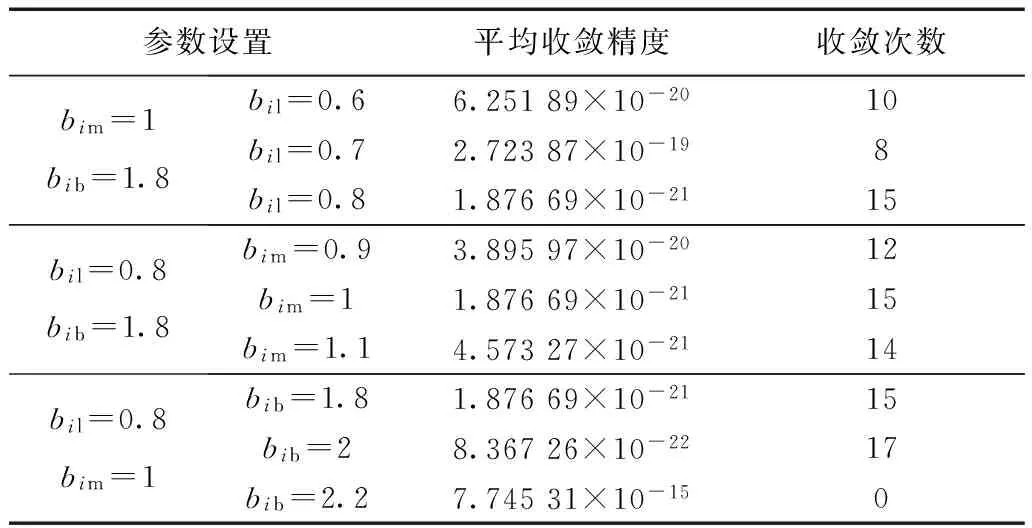

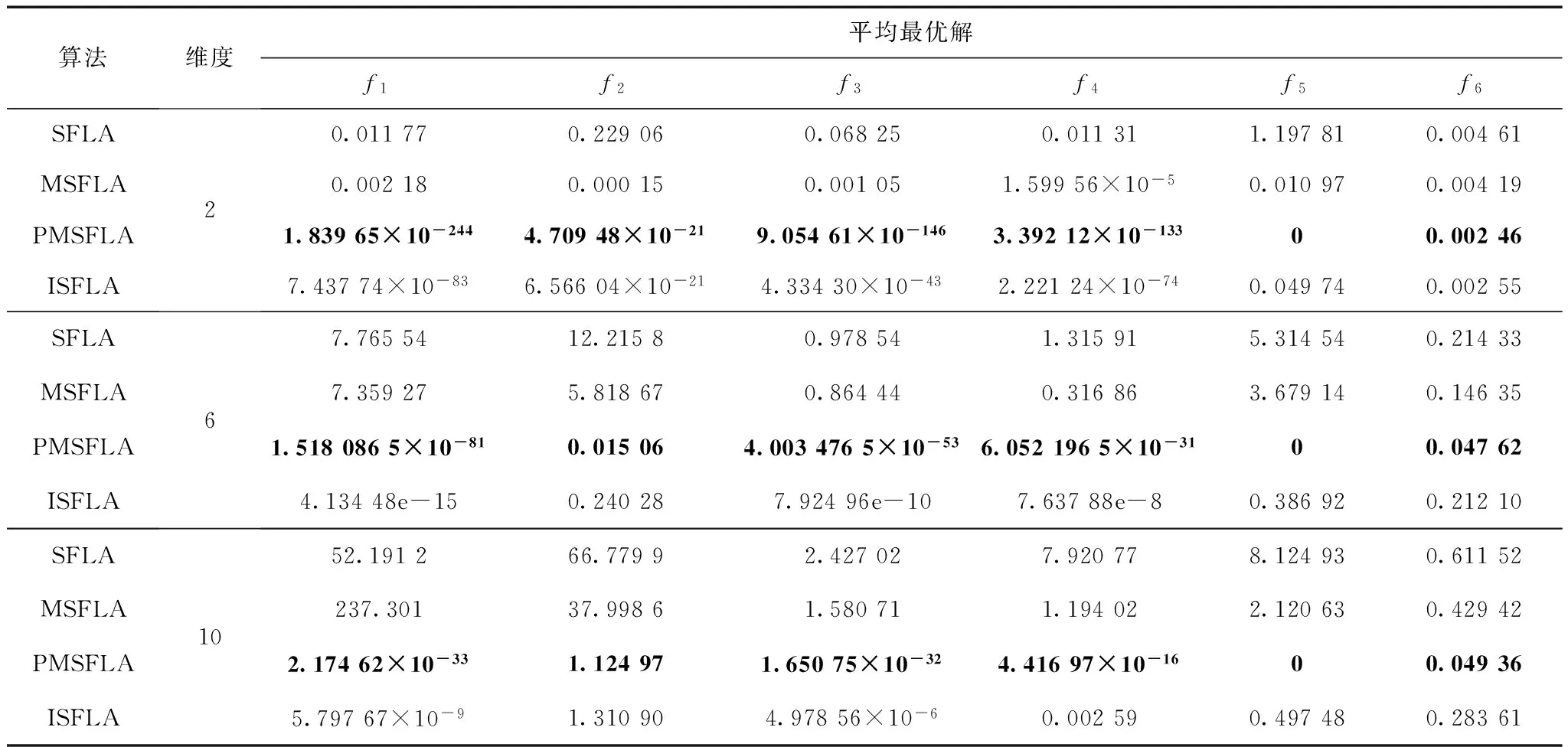
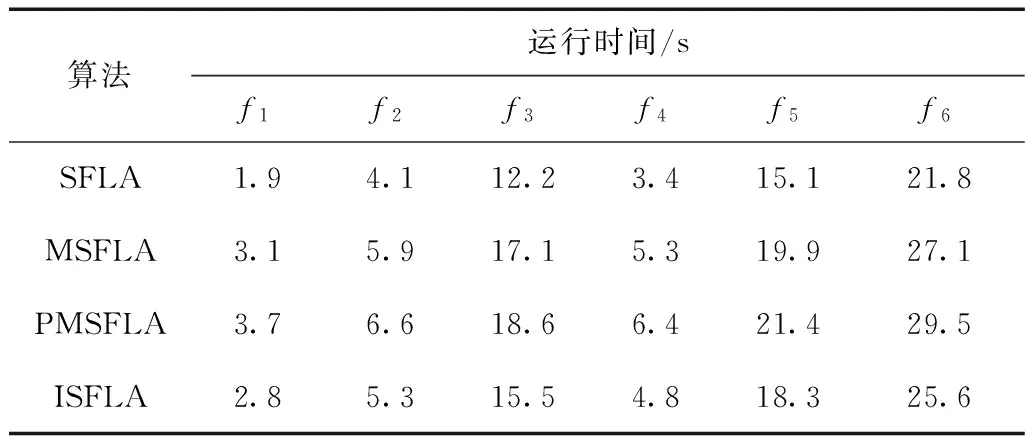
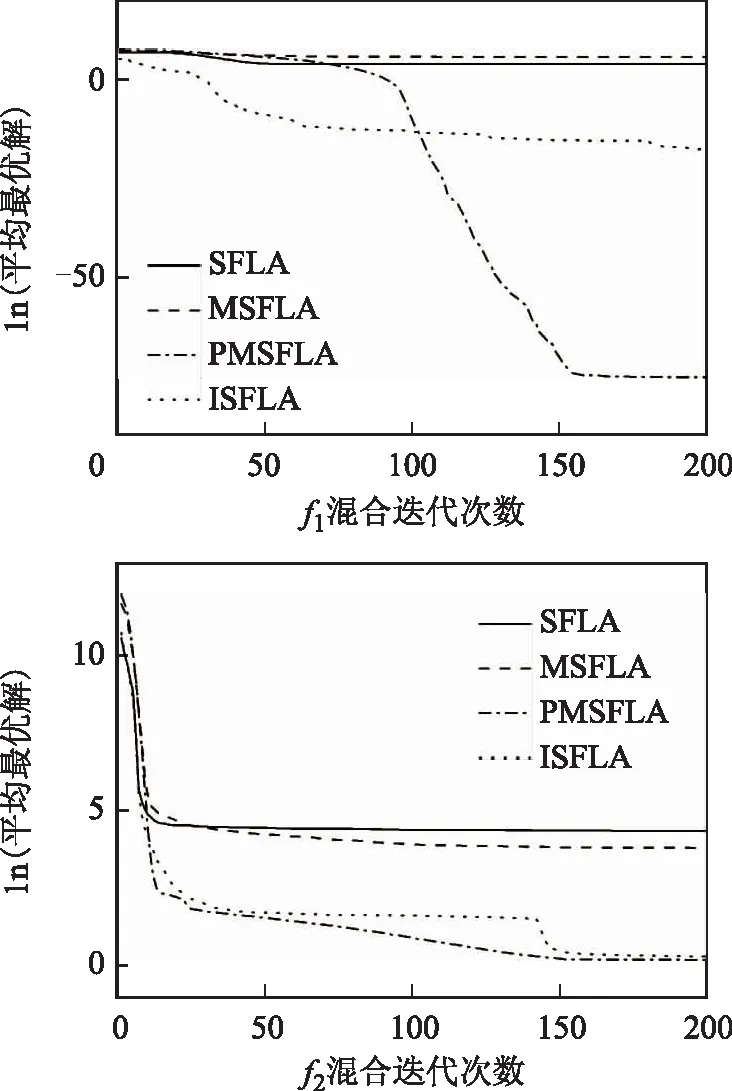
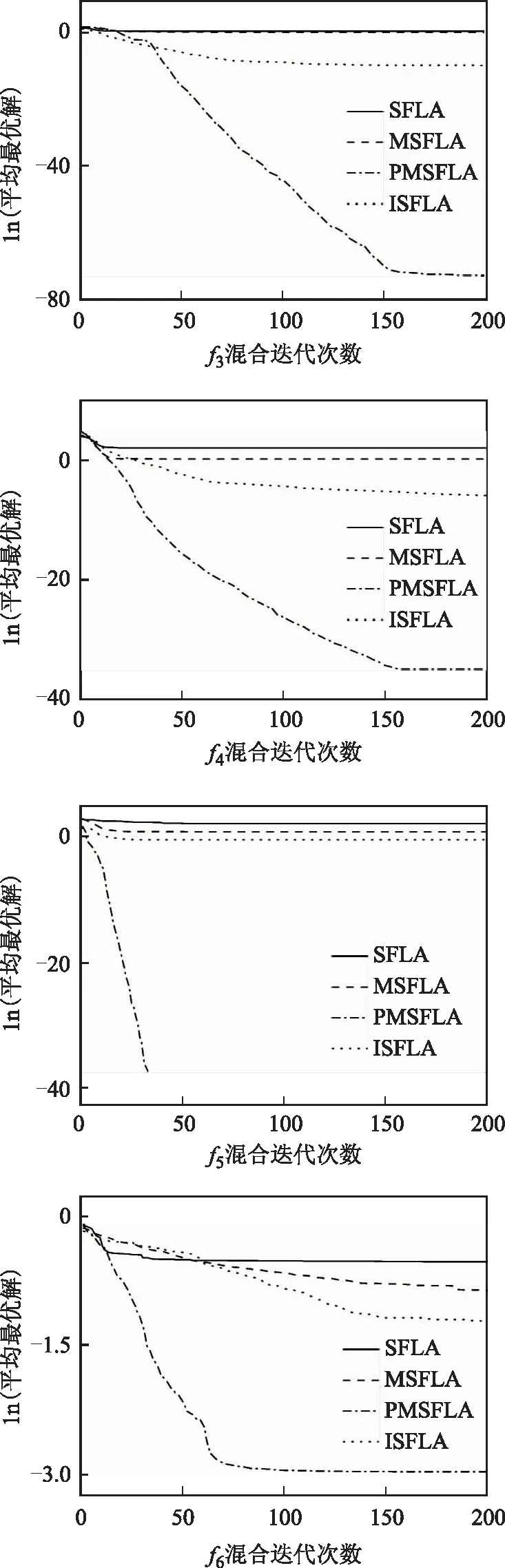


4 實用性驗證

5 結論

