從高考試題例談遺傳定律教學中的若干數理統計問題

艾劍鳴

(浙江省溫州中學 325000)

遺傳學定律是在大量實驗、探究的基礎上逐步建立起來的。實驗和探究離不開數據的收集、處理與解釋，而這通常需要以科學的數理統計方法為基礎。

1 互斥事件的加法原理與獨立事件的乘法原理

在一次實驗中，如果事件A與事件B不同時發生，就叫做A和B互斥(也稱互不相容)，A、B中恰有一個發生的概率，等于事件A、B分別發生的概率的和，即P(A+B)=P(A)+P(B)，此為加法原理。

在實驗中，如果事件A的發生對事件B的發生不產生影響，就叫做A和B是相互獨立的，則A、B同時發生的概率等于事件A、B分別發生的概率的乘積，即P(AB)=P(A)×P(B)[1]，此為乘法原理。

例1 (2016年4月浙江選考題，節選)果蠅的長翅(B)與短翅(b)、紅眼(R)與白眼(r)是兩對相對性狀。親代雌果蠅與雄果蠅雜交，F1表現型及數量如表1。

請回答：

(1)略；

(2)F1長翅紅眼雌果蠅中，雜合子占________；

(3)現有1只長翅白眼果蠅與1只長翅紅眼果蠅雜交，子代雄果蠅中長翅白眼占3/8，則子代雌果蠅中出現長翅白眼的概率為________。

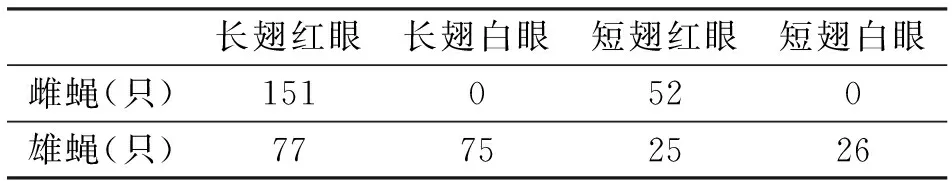
表1 F1表現型及數量

解析：兩處計算均涉及乘法原理應用，難度有梯度遞進，前者只需套用乘法原理，而后者則需理解乘法原理方能靈活應用。具體分析如下：第(2)小題，據表中F1表現型及數量可知，親本為BbXRY×BbXRXr，故F1長翅紅眼雌果蠅基因型為B__XRX-。解法一：可依據加法原理，所求雌果蠅雜合子的基因型包括BBXRXr[其概率為P(甲)=1/6]、BbXRXr[P(乙)=1/3]、BbXRXR[P(丙)=1/3]，故P雜=P(甲)+P(乙)+P(丙)=5/6。解法二：依乘法原理，其翅形基因純合(BB)的概率為P(1)=1/3，眼色基因純合(XRXR)的概率為P(2)=1/2。按獨立事件的乘法原理，故其中純合子的概率P純=P(1)×P(2)=1/6，即雜合子概率為P雜=1-P純=5/6。第(3)小題，常規解題思路：仍可按乘法原理，先將子代雄果蠅中長翅白眼的概率3/8看做兩個獨立事件(即長翅和白眼的概率之積)，后可求出雜交雙親的性別，再由親本求子代雌果蠅出現長翅白眼的概率。但如此解題的話，因計算量大、費時費力，錯誤率高。因而可改進思路：由子代雄蠅有兩種眼色，可知母本為雜合子紅眼果蠅，故父本為白眼(XbY)果蠅，此時其子代雌雄果蠅表現相同，故子代雌果蠅中出現長翅白眼的概率亦為3/8。

例2 (2012年廣東卷)人類紅綠色盲的基因位于X染色體上，禿頂的基因位于常染色體上，結合表2信息可預測，圖1中Ⅱ3和Ⅱ4所生子女是：

A.非禿頂色盲兒子的概率為1/4

B.非禿頂色盲女兒的概率為1/8

C.禿頂色盲兒子的概率為1/8

D.禿頂色盲女兒的概率為0

表2 禿頂基因及其表現型

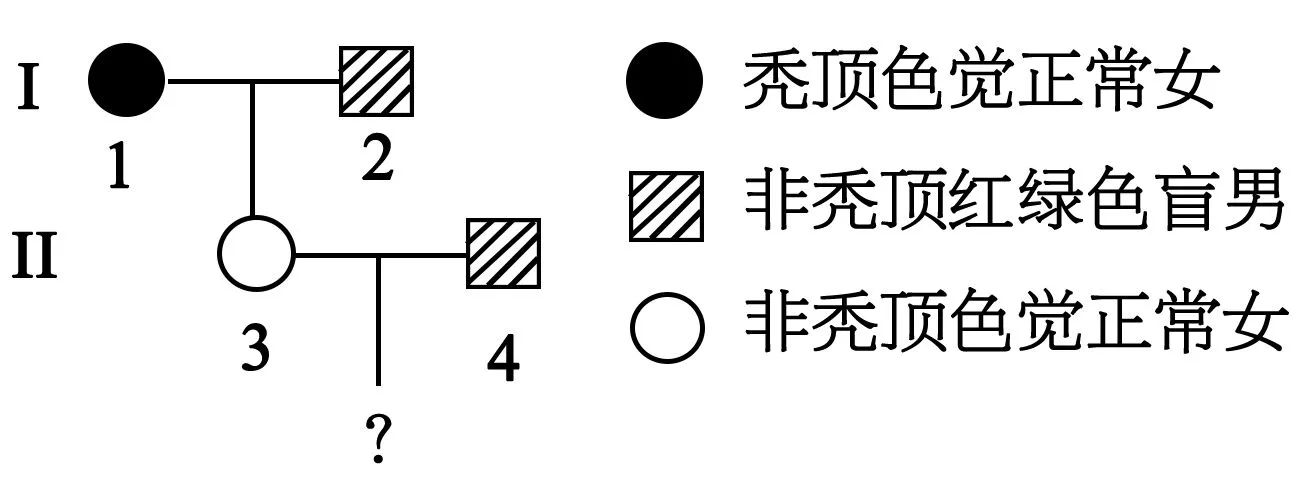
圖1 某家系禿頂/紅綠色盲遺傳圖

解析：據題意，II3的基因型為BbXAXa，II4的基因型為BBXaY。分開考慮，后代禿頂的概率為P(禿)=1/4，P(非禿)=3/4；后代患紅綠色盲的概率為P(色)=1/2，P(非色)=1/2。但因為此時是否禿頂與是否色盲患者及性別都是相關事件而非獨立事件，因此A項中非禿頂色盲兒子的概率是不能用P(非禿)×P(色)×1/2來計算的。正確的解法應該是將兩種性別分開分析，如果是生兒子P(男)=1/2，P(非禿)=1/2，P(色)=1/2，故非禿頂色盲兒子的概率應為上述三者之積，即1/8。或者直接將表現型(非禿頂色盲兒子)轉換為基因型(BBXaY)，此時基因型為BB和基因型為XaY為獨立事件，故其概率P=P(BB)×P(XaY)=1/2×1/4=1/8。同理可求得B選項(非禿頂色盲女兒的概率)為1/4；C選項(禿頂色盲兒子的概率)為1/8；D選項(禿頂色盲女兒的概率)為0。參考答案：CD。

2 二項分布

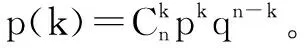
例3 試求一對白化基因的攜帶者夫妻，所生3個孩子中至少有2個正常的概率。

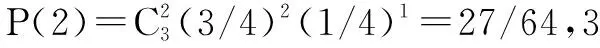
3 數列分析

在一些代數較多的雜交實驗中，隨代數的增加，子代情況的相關運算會變得非常復雜。此時用數列的思想進行分析會使問題化繁為簡。若將各代組成的一個總體看做一個數列，那么每一代的情況即為數列的每一項。因每一代的情況均直接決定于其上一代，那么只要找到每一代與其上一代情況的函數關系，即可運用數列遞推的思想找到Fn中某種個體的比例與代數(n)之間的關系。

例4 (2013年山東卷)用基因型為Aa的小麥分別進行連續自交、隨機交配，連續自交并逐代淘汰隱性個體、隨機交配并逐代淘汰隱性個體，根據各代Aa基因型頻率繪制曲線如圖2，下列分析錯誤的是：

A．曲線Ⅱ的F3中Aa基因型頻率為0.4

B．曲線Ⅲ的F2中Aa基因型頻率為0.4

C．曲線Ⅳ的Fn中純合體的比例比上一代增加(1/2)n+1

D．曲線Ⅰ和Ⅳ的各子代間A和a的基因頻率始終相等

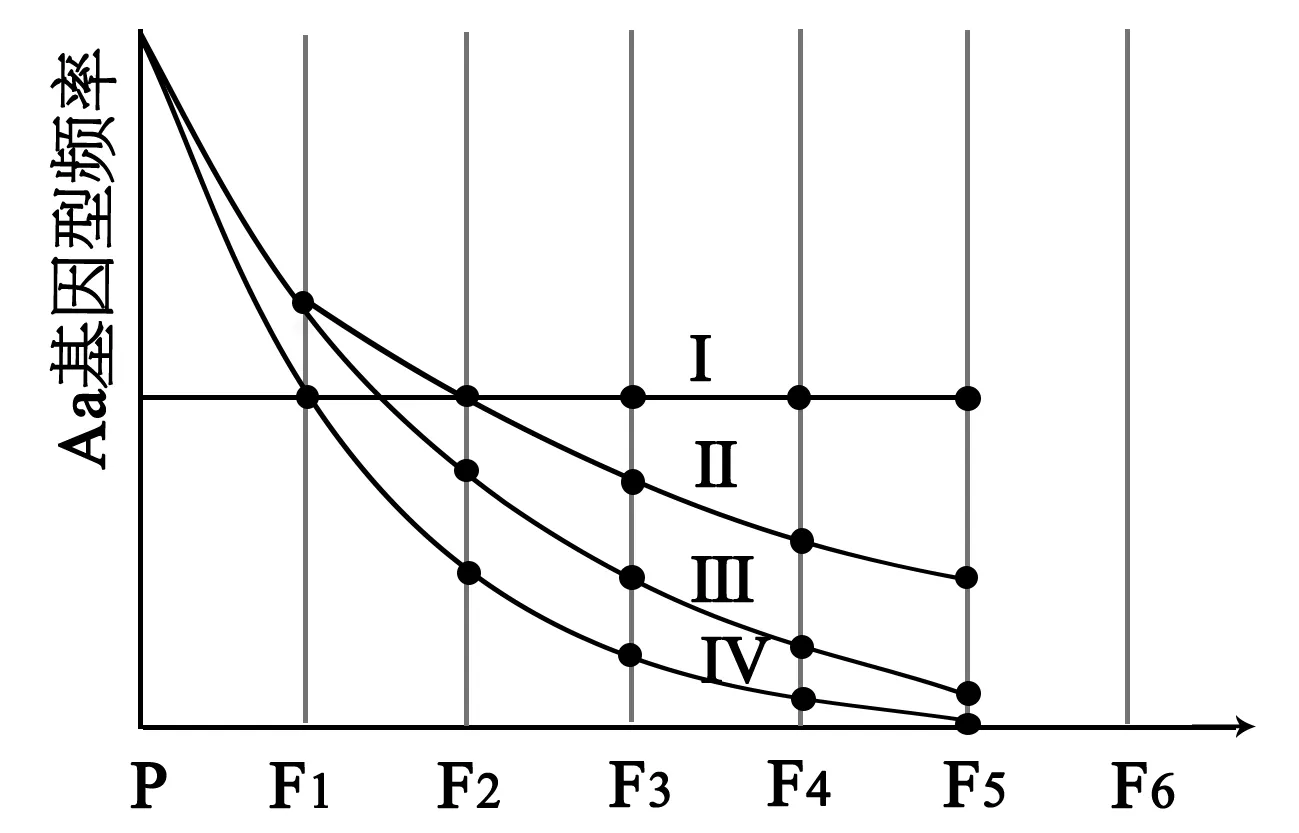
圖2 各代Aa基因型頻率曲線圖

解析：此題考查遺傳學分離定律的應用，涉及到基因頻率和基因型頻率的計算，跳躍性強，計算量大，難度很高。連續自交時，設Fn中Aa基因型頻率為an，an=1/2an-1=1/4an-2=…=(1/2)n-1a1，顯然a1=1/2，故an=(1/2)n，對應曲線為Ⅳ。此時，Fn中純合體的比例比上一代應增加(1/2)n，故C項錯誤。連續自交時，Fn中Aa基因型頻率為an=(1/2)n，AA與aa的基因型頻率均為an=1/2-(1/2n+1)。故連續自交并逐代淘汰隱性個體時，Aa基因型頻率為an=P(Aa)/[P(AA)+P(Aa)]=(1/2n)/[1/2+(1/2n+1)]=2/(2n+1)，對應曲線為Ⅲ。F2中(即n=2時)Aa基因型頻率為2/5，故B項正確。隨機交配且無選擇因素時，Aa基因型頻率不發生變化，故an=a1=1/2，對應曲線為Ⅰ。結合上述對曲線Ⅳ的分析可知，D項正確。隨機交配并逐代淘汰隱性個體時，令Fn-1中Aa基因型頻率為an-1，則Fn-1中a基因頻率為p=an-1/2，A基因頻率為q=1-(an-1/2)。依據遺傳平衡定律，淘汰隱性個體前，Fn中AA基因型頻率為q2，Aa基因型頻率為2pq。故淘汰隱性個體后，Fn中Aa基因型頻率為an=P(Aa)/[P(AA)+P(Aa)]=2pq/(q2+2pq)，將p、q代入后得an=an-1/[1+(an-1/2)]，兩邊取倒數得1/an=(1/an-1)+1/2=(1/a1)+[(n-1)/2]。因此，a1(F1中Aa基因型頻率)為2/3，代入前式得1/an=(n+2)/2，故an=2/(n+2)，對應曲線為Ⅱ。F3中(即n=3時)Aa基因型頻率為2/5，故A項正確。參考答案：C。

4 分離比的檢驗

孟德爾豌豆相對性狀的雜交實驗中，F2的分離比有些與3∶1的理論分離比偏差很小。例如，子葉顏色為黃色：綠色=6022∶2001(3.01∶1)，種子形狀為圓形∶皺形=5474∶1850(2.96∶1)，將此偏差視為測量所允許的誤差范圍，學生有很高的認同度。但有些與3∶1的理論分離比偏差相對較大。例如，花色為紫色∶白色=705∶224(3.15∶1)；豆莢顏色為綠色∶黃色=428∶152(2.82∶1)，此偏差是否仍在測量允許的誤差范圍，學生意見不盡相同。

測量允許的誤差范圍需要用一定的統計方法進行檢驗。例如，分離比的檢驗常采用χ2(卡方)作為實測值與理論值總偏差的一種統計量，然后進行適合性檢驗[1]。即將此χ2值與臨界值作比較，可以看出此偏差是否在誤差允許的范圍。

例5 孟德爾關于黃色圓粒和綠色皺粒豌豆的雜交實驗，共獲得556粒F2代種子，其中黃色圓形、黃色皺形、綠色圓形和綠色皺形依次為315、101、108和32粒。試問此結果是否符合9∶3∶3∶1的分離比？

解析：χ2值的計算公式之一為圖3。其中fi為實測頻數，即F2中某一表現型的實際數量，E(fi)為理論頻數，即按9∶3∶3∶1的理論分離比計算所得的F2代中某一表現型的數量。故χ2=(315-312.75)2/312.75+(101-104.25)2/104.25+(108-104.25)2/104.25+(32-34.75)2/34.75=0.470。本例中自由度df=4-1=3，查χ2值表(一尾)可知χ2<0.58，即P>0.90。也就是說，可以有90%的置信水平認為此分離比符合9∶3∶3∶1的理論分離比。

圖3 X2值的計算公式

對一對相對性狀的分離比及模擬實驗的分離比可用同樣的方法進行檢驗。并且此方法可在常用的EXCEL中通過編輯公式完成。因而可以在向學生簡單闡明檢驗原理后，快速檢驗實驗數據并向學生直觀呈現檢驗結果。讓學生不但知其然，更知其所以然。