基于聯合仿真的汽車半主動懸架模糊控制分析

郝博然 卞學良 竇占峰 朱玉剛

（1.河北工業大學；2.中國汽車技術研究中心）

懸架的性能對汽車平順性和操穩性影響顯著。半主動懸架則可以根據不同路況改變阻尼或剛度的大小，性能較被動懸架有很大提升。和主動懸架相比，半主動懸架在性能接近的同時又具有安全性好、成本低及結構緊湊等優點。高性價比使得半主動懸架愈來愈受到國內外研究人員的關注。以往人們在對車輛動力學模型進行分析時，大多建立數學模型進行分析，而數學建模過程繁瑣，利用軟件搭建的數學模型可視化和可讀性也較差，在一定程度上降低了工作效率和精度[1-3]。文章通過運用LMS.AMESim軟件并基于物理意義對半主動懸架1/4車進行建模，建模思路清晰。然后利用MATLAB/Simulink設計了模糊控制器，對半主動懸架模型進行聯合仿真，并對仿真結果進行分析，分析結果表明，采用模糊控制的半主動懸架較被動懸架性能有較為明顯的改善，同時聯合仿真的方法提高了工作效率和準確率，對半主動懸架的后續研究具有參考意義。

1 動力學模型分析

1.1 半主動懸架1/4車模型分析

汽車是一個復雜的振動系統，其振動形式和振動的影響因素繁多。但在研究不同問題時，可以在一些合理假設的基礎上，將汽車簡化為相應的簡易模型進行分析。1/4車模型可以很好地反映垂直振動對汽車平順性的影響，該模型能夠仿真汽車乘坐舒適性、輪胎動載荷及懸架動行程[4-6]。半主動懸架1/4車模型，如圖1所示。

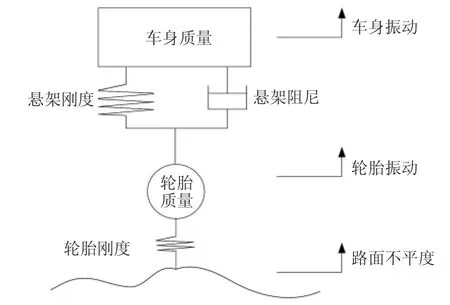
圖1 半主動懸架1/4車模型圖

在該模型中，考慮了路面不平度輸入、車身質量、輪胎質量、懸架的剛度和阻尼及輪胎剛度，忽略了輪胎阻尼的影響。根據牛頓運動定律，對車輪和車身進行動力學分析，得到微分方程組，如式（1）所示。

式中：m1，m2——輪胎質量和車身質量，kg；

q，z1，z2——路面不平度輸入、輪胎垂直位移和車身垂直位移，m；

Kt——輪胎剛度，N/m；

K——懸架剛度，N/m；

C——半主動減振器的可變阻尼值，N/m·s；

C0——減振器基值阻尼，N/m·s；

CS——半主動減振器阻尼值的變化量，N/m·s。

通過節流口面積的變化，半主動懸架阻尼值可以相應改變，將減振器阻尼值設置為3檔，分別實現阻尼的“軟”、“中”及“硬”調節。模型的結構參數為：m1=35.85kg，m2=411.5kg，K=20200N/m，Kt=250000N/m，C0=1 600 N/m·s。

1.2 隨機路面模型建立

通常情況下有2種方法產生隨機路面不平度：1）白噪聲信號通過濾波器作用產生濾波白噪聲；2）白噪聲信號通過積分器作用產生積分白噪聲[7]。由于我國B級和C級路面占比重大，故選用譜密度為的積分白噪聲信號來模擬C級隨機路面，路面不平度（q（t）/m）的關系式，如式（2）所示。

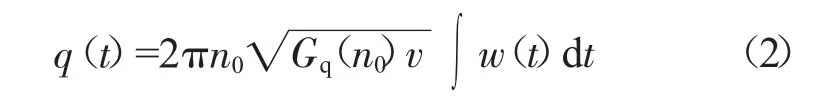
式中：w（t）——白噪聲信號，其均值為0；

n0——參考空間頻率，m-1，此處n0=0.1；

Gq（n0）——路面不平度系數，m3，C級路面為256×10-6m3；

v——車速，m/s，此處v=20 m/s。

通過MATLAB/Simulink對C級路面模型進行仿真，仿真曲線，如圖2所示。

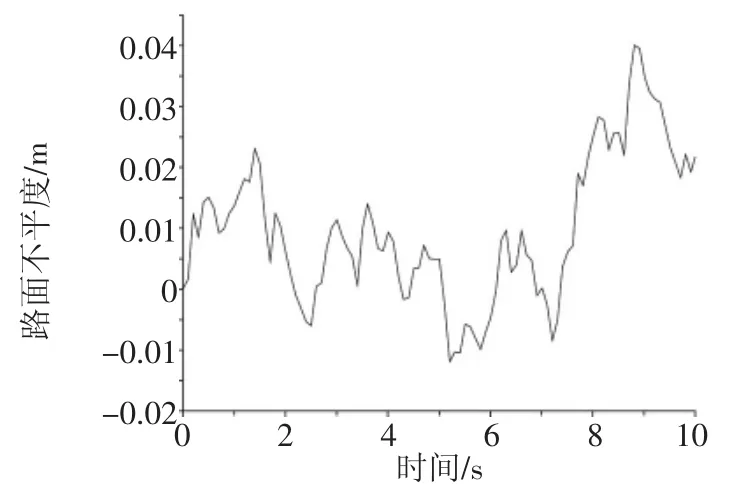
圖2 C級隨機路面仿真曲線圖

2 模糊控制器的設計

模糊控制是智能控制的重要組成部分。模糊控制系統魯棒性好，外界因素干擾和系統參數的改變對控制效果的影響較小，因此模糊控制對復雜的非線性時變系統尤為適合[8]。汽車懸架是一個復雜的非線性時變系統，選用模糊控制能夠得到較為理想的控制效果。文章設計一個二維模糊控制器來實現對減振器阻尼的調節控制，實現半主動懸架阻尼值在“軟”、“中”及“硬”三態切換。

2.1 模糊控制器結構

車輛懸架動撓度（z2-z1）與期望值0的差值設為偏差（E/m)；設為變化率（EC/（m/s）），將E和EC作為模糊控制器的輸入變量，CS為輸出變量。半主動懸架模糊控制流程，如圖3所示。E和EC均采用7個模糊語言值：｛負大、負中、負小、零、正小、正中、正大｝，即｛NB，NM，NS，ZO，PS，PM，PB｝。模糊控制器輸出量采用3個語言值｛軟，中，硬｝，即｛S，M，H｝。

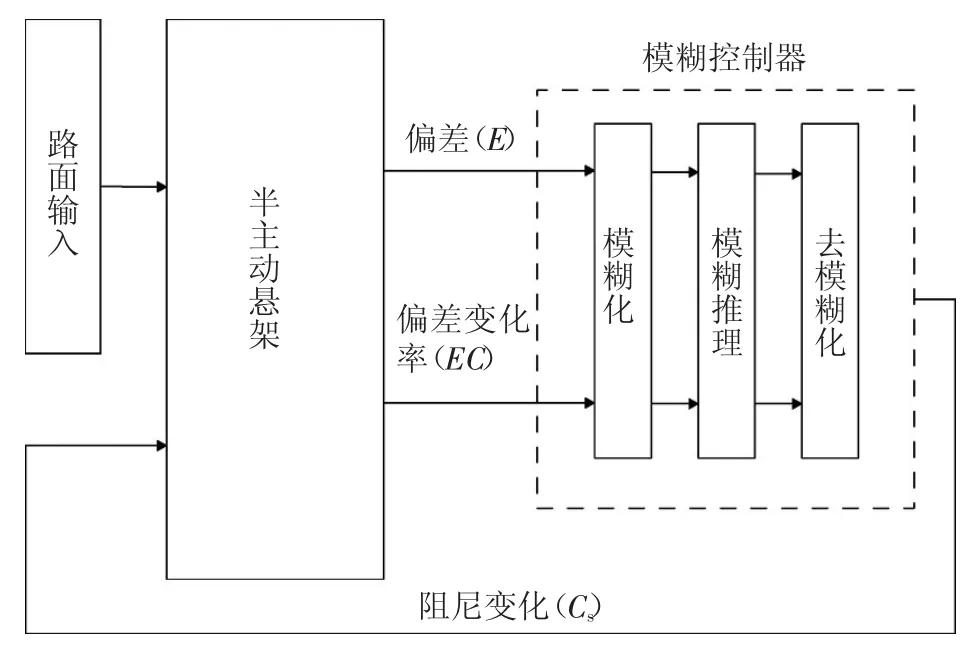
圖3 半主動懸架模糊控制流程圖

2.2 半主動懸架模糊控制器參數確定

2.2.1 基本論域

模糊控制器的輸入和輸出是和路面不平度輸入緊密相關的。路面隨機變化，輸入量也會隨機改變，因此應根據變化范圍的最大值來確定基本論域[9]。通過仿真分析，確定了模糊控制器輸入和輸出量的基本論域。E和 EC 的基本論域分別為[-0.017，0.017]和[-3，3]；CS的基本論域為[-800,800]

2.2.2 模糊論域

將E和EC離散為13級，模糊論域為｛-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6｝。CS的模糊論域為｛-1，0，1｝，-1 對應阻尼負變化，此時減振器為“軟”；0 對應減振器的軟硬程度為“中”；1對應減振器阻尼變大，此時減振器為“硬”。

2.2.3 量化因子

在基本論域和模糊論域確定后，可以得到量化因 子 KE=6/0.017=352.94，KEC=6/3=2， 比 例 因 子KCS=800/1=800。

2.3 確定控制規則

設計模糊控制器的核心部分是確定模糊控制規則[10]。以懸架動行程及其變化率為輸入量。設計控制規則的核心思想是：1）當懸架動撓度較大，且當變化量有增大的趨勢時，應增大阻尼力以抑制動撓度的增大；2）當動撓度大，但其變化率使當前變化量有反向變化的趨勢時，可減小阻尼值來減小車輛振動；3）當動撓度小，變化率小，應減小阻尼來衰減車輛振動[11]。在上述原則指導下，并結合大量仿真調試，制定模糊控制規則，如表1所示。輸入量和輸出量的隸屬函數均選擇三角形函數（Trimf），推理邏輯選擇Mamdani法。

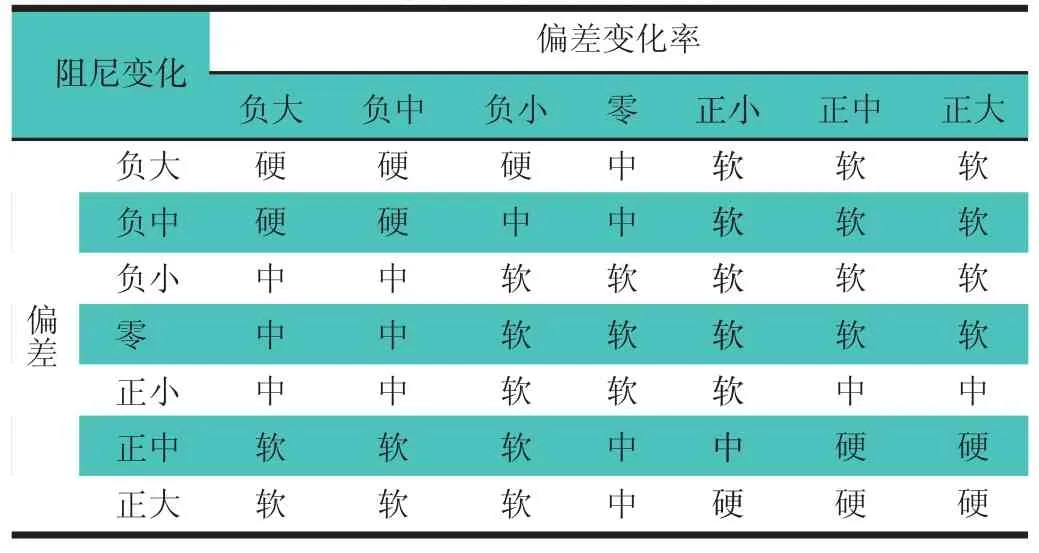
表1 模糊控制器控制規則表

3 AMESim和MATLAB聯合仿真

3.1 仿真模型的建立

在AMESim的草圖模式下，選擇機械庫和信號庫中的部分元件，根據已建立的懸架動力學模型，搭建被動懸架1/4車模型和半主動懸架1/4車模型，如圖4所示。并在模型中添加自定義接口Interface模塊，實現與MATLAB/Simulink的通信，2個接口模塊分別代表模糊控制器和路面，可為懸架模型提供控制器的輸出阻尼和路面不平度輸入。

圖4 AMESim懸架1/4車模型圖

在MATLAB/Simulink操作界面，根據前面分析的設計結果，搭建路面輸入和模糊控制器模型，如圖5所示。圖5中的懸架動力學模型為MATLAB中的S函數模塊，它能夠調用AMESim生成的執行文件，實現與AMESim的通信。懸架動撓度及其變化率經量化后傳遞給模糊控制器，經模糊推理后得出輸出變量，乘以比例因子后再反饋給懸架模型，實現聯合仿真。

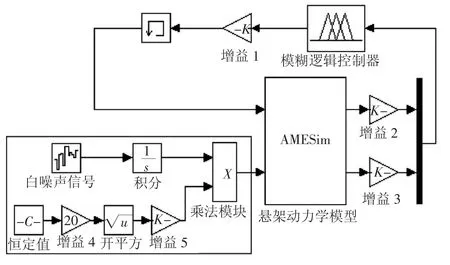
圖5 模糊控制器及路面輸入模型圖

3.2 仿真結果及分析

通過對被動懸架和半主動懸架的仿真分析，得到兩者的車身垂直加速度對比圖、車輪動載荷對比圖及懸架動撓度對比圖，如圖6～圖8所示。

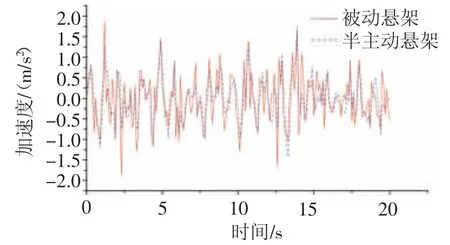
圖6 車身垂直振動加速度對比圖

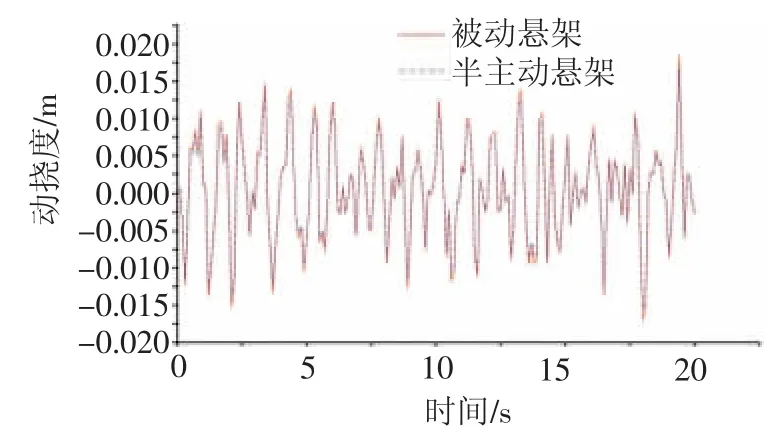
圖7 懸架動撓度對比圖

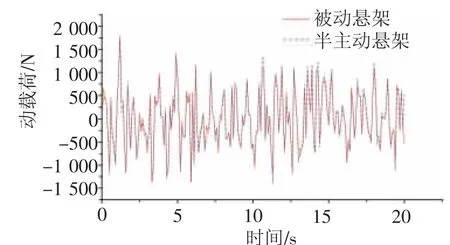
圖8 車輪動載荷對比圖

由圖6～圖8可以看出，當汽車以20 m/s的速度行駛在C級路面時，采用模糊控制的汽車車身垂直動加速度有較為明顯的降低，懸架動撓度也有一定程度的降低，輪胎動載荷變化不大，懸架響應均方根值對比，如表2所示。

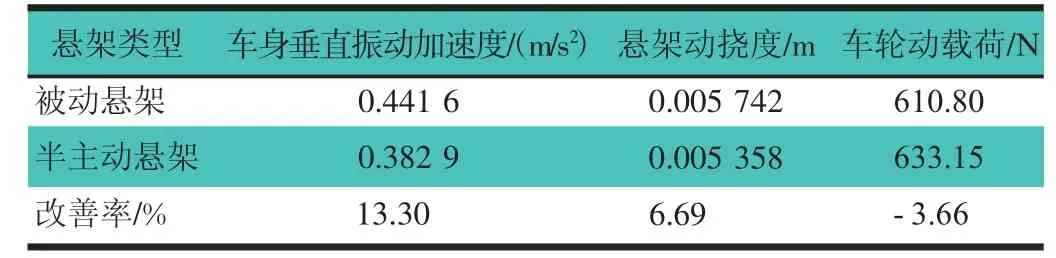
表2 懸架響應均方根值對比表

由表2可知，車身垂直振動加速度均方根值降低了13.30%，懸架動撓度均方根值降低了6.69%，車輛乘坐舒適性和操縱穩定性均得到了不同程度的改善；輪胎動載荷均方根值略有增加，增大3.66%，幅值增加3.39%，均增加不大，且在可承受范圍之內，對車輛的影響可以忽略不計。因為車身垂直振動加速度、懸架動撓度及輪胎動載荷之間是相互制約相互影響的，一般只能改善其中1個或2個指標。綜上，文章設計的模糊控制器設計合理，在本模糊控制策略控制下的半主動減振器性能較被動減振器有較為理想的改善。

4 結論

1）AMESim軟件界面簡潔，建模方便，省去了數學方程推導的繁瑣過程，與MATLAB/Simulink聯合仿真的方法可行有效。

2）文章設計的模糊控制器結構合理，控制規則有效，對半主動減振器具有良好的控制效果。車身垂直振動加速度和懸架動撓度得到改善，汽車乘坐舒適性和操縱穩定性得到提高。輪胎動載荷均方根值和幅值增加很小，影響甚微。所設計的控制器控制效果良好。