EKF在非機動單站無源探測中的應用研究

作者/謝磊、劉宇暢、聶楊，中國電子科技集團公司第二十九研究所

EKF在非機動單站無源探測中的應用研究

作者/謝磊、劉宇暢、聶楊，中國電子科技集團公司第二十九研究所

非機動單站純方位無源定位系統能估計出遠處作勻速直線或分段勻速直線運動的輻射源的運動方向、與觀測站的粗略距離等。利用非機動單站無源系統捕獲的這些信息，可以在保持“電磁隱蔽”的前提下，進行軍事行動及裝備部署，因此有著重要的軍事應用價值。本文研究了擴展卡爾曼濾波（EKF）在非機動單站無源探測系統中的應用。

非機動單站無源定位；純方位定位；卡爾曼濾波

引言

ESM作為電子戰的一部分，是利用敵方電磁輻射而采取的軍事支援行動，包括對電磁輻射信號的搜索、截獲、識別、定位等，從而為其它軍事行動提供依據[1]。其中，對目標的無源定位有重要意義。

常見的無源定位分為機動平臺對靜止目標（慢速移動目標）的定位和非機動平臺對移動目標的定位。關于前者的相關研究比較多，而后者其實也有著重要研究價值，非機動地面觀測站有“電磁隱蔽”和“長時間值守”等優點，特別適合布置于沿海一帶，偵察相關空域。本文分析了非機動單站純方位無源定位系統，對比了最小二乘法和卡爾曼濾波在該系統估計中的應用。

1. 最小二乘法原理

當輻射源距離觀測站很遠時，可近似認為輻射源做勻速直線運動或分段直線運動（速率恒定，運動方向恒定）。如圖1所示，設觀測站（靜止）位于坐標原點，輻射源由遠及近，做勻速直線運運動。系統觀測量為?k、θk（k=0,1,……,對應不同的時刻）。設觀測站與輻射源的距離為rk（k=0,1,……）,則輻射源的位置Tk( rk,θk,?k)，k=0,1,……。設輻射源的速率是v，速度方向為(α,β)，其中α是速度矢量在xoy面的投影與y正向的夾角，β是速度矢量與z正向的夾角。

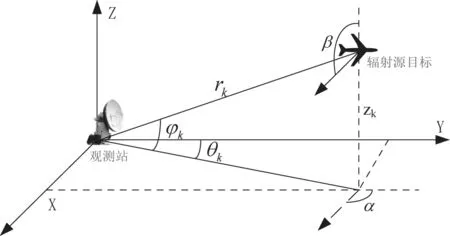
圖1 非機動單站純方位無源定位系統的示意圖

輻射源在任意k時刻的狀態可用球坐標系來確定(rk,θk,?k,v,α, β)，其中?k、θk為系統觀測量。在直角坐標系中，輻射源在時刻k的位置可表示為(xk,yk,zk)，速度矢量為(vx, vy, vz)，可得：

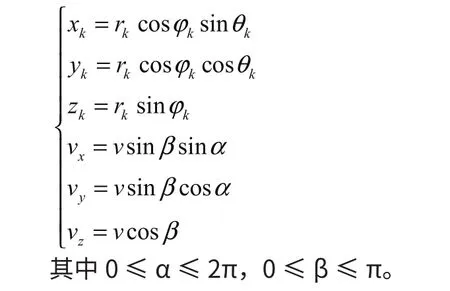
用(xk,yk,zk, vx, vy, vz)也可表示輻射源的狀態。在直角坐標系中可利用球坐標中的角度分量?k、θk和距離分量rk，于是k時刻輻射源的位置表示為：

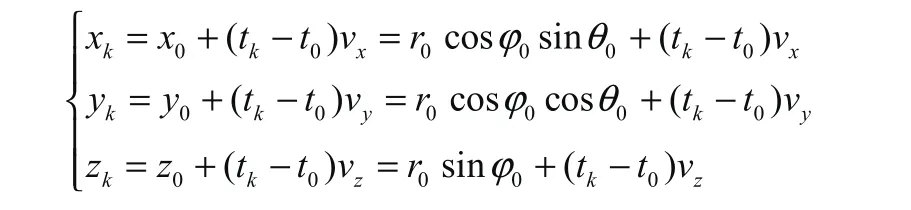
系統方程可表示為：

其中，Wk—1是狀態噪聲，V1k、V2k是觀測噪聲

觀測量?k、θk滿足下列方程：

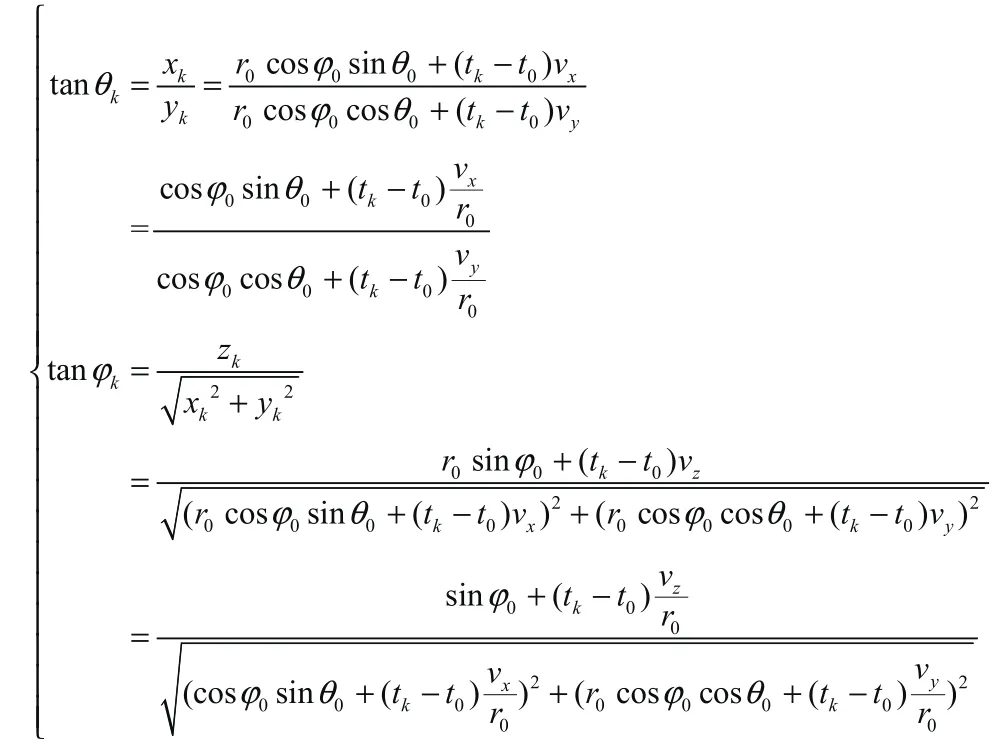
根據上式，用最小二乘法[2]估計出vx/r0、vy/r0、vz/r0。

利用上述方程組的第1個公式，可得：

利用前k個時間內的歷史數據進行計算，得到：

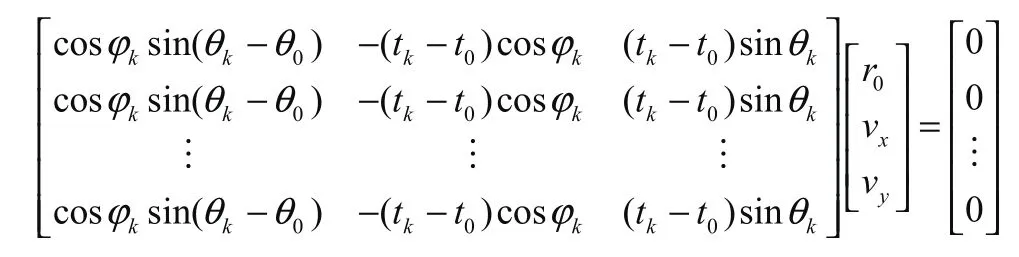
設系數矩陣第1列為A1，第2、3列為A2，則有：

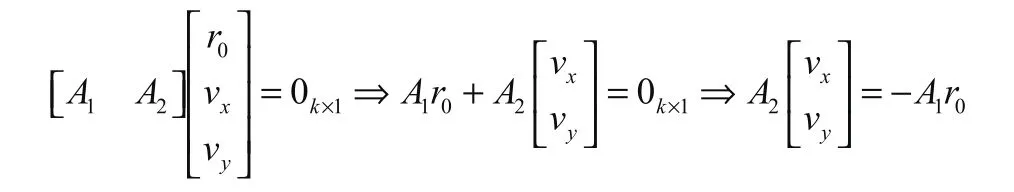
令z0=[vx/r0vy/r0]T，則上式可轉換為A2Z0= —A1；

根據文獻[15]所提出的方法，用最小二乘法求解，得：

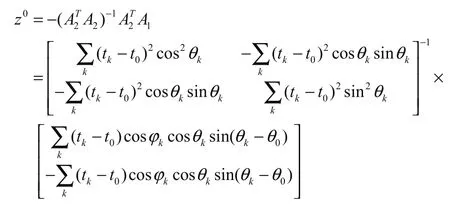
2. EKF算法原理

采用擴展卡爾曼濾波對vx/r0、vy/r0、vz/r0進行估計，Z0=[ vx/r0、vy/r0、vz/r0]T。系統方程表示：

系統的觀測方程非線性[3]，可使用EKF方法進行估計，假設系統噪聲滿足下列條件：

EKF算法[4][5]如下，設初值(狀態向量的估計值) ; P0|0(估計的均方誤差陣)，滿足：

此時，使用EKF同時估計出系統的三個狀態值vx/r0、vy/r0、vz/r0。

3. 仿真對比

場景：觀測站靜止，坐標為(0，0，0)(m)，輻射源勻速直線運動，初始坐標(1051055×103)(m),速度矢量為(300—300 0)(m/s)，觀察站與輻射源初始距離為2×105(m),速度約424(m/s),方向為(130，90)(度)。假設方位角、俯仰角度觀測噪聲都服從N(0,0.012)。

（1）利用最小二乘法對輻射源的運動方向(α,β)進行估計，仿真如圖2所示。

（2）利用EKF算法對輻射源的運動方向(α,β)進行估計，仿真如圖3所示。

對比圖2和圖3的仿真結果可知：

①在前40次迭代中，最小二乘法總體趨勢收斂，但波動較大；而EKF持續收斂，并無波動；

②最小二乘法迭代85次后，角度誤差持續小于5度；而EKF迭代50次后，誤差就已持續小于5度。

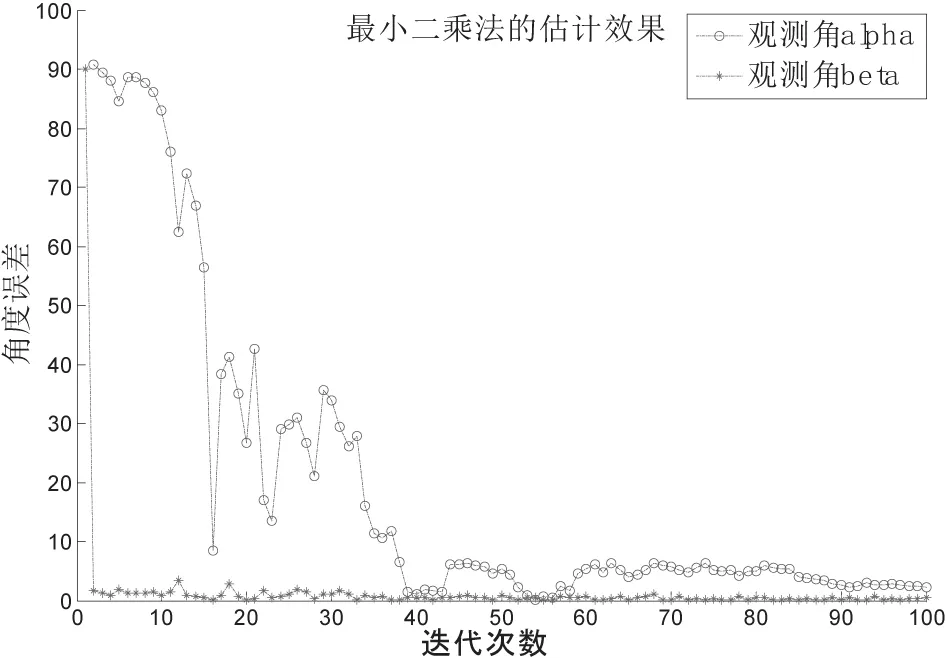
圖2 最小二乘算法仿真

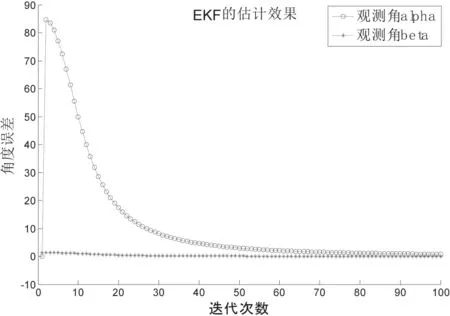
圖3 EKF算法仿真

4. 結論

本文對最小二乘法和EKF算法進行了原理介紹，并利用MATLAB對二者進行了建模仿真。最小二乘法需要很多歷史數據，對該數據進行“塊計算”，而卡爾曼濾波能“忽略歷史數據”，做到節省計算量。仿真結果表明，EKF比最小二乘法收斂更快、精度更高。

＊ [1]趙國慶，雷達對抗原理[M]，西安：西安電子科技大學出版社，1999

＊ [2]董志榮，純方位系統TMA非線性最小二乘法—理論數學模型與常規算法[J]，情報指揮控制系統與仿真技術，第27卷，第1期，2005年2月

＊ [3]鄭大鐘，線性系統理論（第2版）[M]，清華大學出版社，2002年10月

＊ [4]袁天鑫，最佳估計原理[M]，國防工業出版社，1980年

＊ [5]詹艷梅，純方位目標運動分析卡爾曼濾波算法[J]，應用聲學，22卷，1期