雨水泵站水泵機組啟停優化
王 昊,張永祥,唐 穎,劉 宇,李凱旋
(1.北京工業大學 建筑工程學院,北京 100124;2.水質科學與水環境恢復工程北京市重點實驗室(北京工業大學),北京 100124)
雨水泵站水泵機組啟停優化
王 昊1,2,張永祥1,2,唐 穎1,2,劉 宇1,2,李凱旋1,2
(1.北京工業大學 建筑工程學院,北京 100124;2.水質科學與水環境恢復工程北京市重點實驗室(北京工業大學),北京 100124)
為解決雨水泵站運行過程中存在的水泵頻繁啟停問題,提出一種水泵機組啟停優化方法.該方法通過分析泵站的設計參數和水泵機組運行原理,建立啟泵水位優化模型,并運用暴雨洪水管理模型(storm water management model,SWMM)和粒子群優化算法(particle swarm optimization algorithm, PSO)對模型求解,最終得到水泵機組的最優啟泵水位.通過實例將優化方法與傳統的人工調試方法進行對比,驗證了其可行性.研究結果表明:采用優化方法得到的啟泵水位可使機組啟停次數達到最小,實現了較好的水泵啟停效果.同時優化方法也避免了復雜的人工調試過程,得出的優化結果為雨水泵站啟泵水位的選取提供參考.
雨水泵站;啟停優化;暴雨洪水管理模型;粒子群優化算法;最優啟泵水位
在城市排水系統中,雨水泵站的水泵機組在運行過程中經常會出現頻繁啟停現象,這一現象往往是由于啟泵水位設置不當造成的.若水泵頻繁啟停,則會對其自身造成嚴重損害,減少使用壽命[1-3].解決該問題的關鍵在于如何準確、合理地設置啟泵水位,使得機組在運行過程中啟停次數最少,將損害降至最低.對此,相關學者做了一定研究.郭磊等[4]采用人工經驗調試和水力模型相結合的方法,首先對泵站設計參數進行分析并擬定每個泵的啟泵水位,然后運用水力模型進行模擬得到水泵啟停次數.反復經歷這一調試過程,最終通過比較獲得啟停次數最少的啟泵水位組合,作為水泵機組的最優啟泵水位.該方法也是目前較常用的方法,但其人工調試過程較繁瑣,同時存在無法確定的人為因素,較難得到理想的啟停效果.
暴雨洪水管理模型(storm water management model,SWMM)是一款較為成熟、應用廣泛的城市排水系統模擬軟件,其對雨水泵站運行的模擬同樣得到了廣泛應用[5].為解決以上問題,本文通過分析雨水泵站設計參數,建立啟泵水位優化模型,并將SWMM模型與優化算法相結合對目標函數進行求解,確定機組的最優啟泵水位組合,使得啟停次數最少,進而解決水泵頻繁啟停問題.
1 啟泵水位優化原理
設計雨水泵站時需要對蓄水池的有效容積、底面積、最高設計水位和最低設計水位,以及水泵的流量、臺數、啟泵水位和停泵水位進行設計.《室外排水規范》中規定:蓄水池有效容積依據上游設計流量和下游設計流量進行計算;水泵機組總流量依據下游設計流量而定,水泵宜選用同一型號且數量在2~8臺之間;水池的最低設計水位(通常作為停泵水位)根據所選水泵吸水頭的要求而定,最高設計水位一般與進水管的管頂相平;有效容積為最高、最低設計水位之間的體積;池底面積依據有效容積和最高、最低設計水位計算;以上設計參數確定后,要設置啟泵水位使其滿足當水泵機組為自動控制時每小時開泵次數不得超過6次[6].蓄水池設計參數如圖1所示.當遭遇一場降雨事件時,雨水進入管網并匯流至蓄水池上游進水管,通過進水管流入水池.若降雨過程和水池上游管網系統不變,則管網的匯流過程就不變,流入蓄水池的水量也確定不變.因此,當其他設計參數確定后,對于同一場降雨,影響水泵啟停次數的因素僅有啟泵水位.
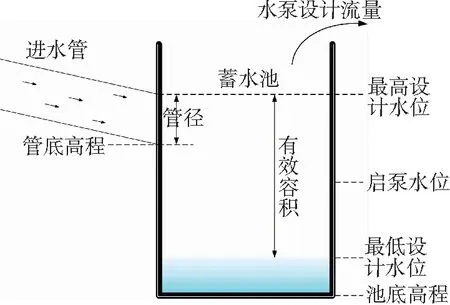
圖1 蓄水池設計參數示意
雨水泵站的水泵數量要在2臺以上.在設置每臺泵的啟泵水位時要按照由低到高合理設置,使得當降雨較小時只有一個泵工作,隨著降雨增大,再依次開啟其他泵.只有這樣設置才可保證水泵啟停次數較少.啟泵水位設置的過高或過低都會增大啟停次數,容易造成頻繁啟停現象,很難滿足規范要求[7-9].最佳啟泵水位可利用水力模型經過反復調試來獲得.本文選用SWMM模型進行優化研究.SWMM能夠模擬降雨、地表徑流和管網匯流的過程,其中也包含了通過設置啟泵水位來模擬水泵的啟停過程.將上游排水管網、下游水池、水泵的設計數據以及當地重現期的設計降雨作為輸入,構建SWMM模型,然后在模型中設置啟泵水位進行模擬,并通過模型結果中的水泵流量過程獲得啟停次數(泵流量從0變為大于0再變回0為一次啟停).經過反復調試并對比每次調試的啟停次數,即可得到較合適的啟泵水位.但此方法的調試過程較繁瑣,耗費大量精力.
為避免此問題,可通過構建優化模型來優化啟泵水位.雨水泵站通常選取單頻泵并聯工作,因此,本文主要針對由單頻泵組成的水泵機組進行優化研究.將降雨、管網、水池、水泵等數據輸入SWMM中構建SWMM基礎模型.在基礎模型之上以機組所有水泵的總啟停次數為優化目標,以每個水泵的啟泵水位為優化變量建立優化目標函數,即
Nmin=minF(h1,h2,…,hn).
(1)
式中:Nmin為所有水泵的總啟停次數,h1,h2…hn為每臺水泵的啟泵水位.在SWMM基礎模型中設置不同的啟泵水位組合便可模擬并獲取相應組合的啟停次數,進而求解目標函數.
建立目標函數后還需確定自變量h1~hn的約束范圍.每臺水泵啟泵水位的設置均要小于最高限值Hmax,并保證在SWMM模擬計算過程中水池的水位不會超過最高設計水位.同時Hmax也要小于最高設計水位.在機組工作過程中,當池內水位達Hmax時,所有水泵均為開啟狀態.假設在進水管流量大于各水泵流量總和的這些時間段內,進水管入流體積之和為V1,如圖2、式(2)和(3)所示.

圖2 流量截取示意
(2)
(3)
式中:Si為進水管出流量大于水泵總流量的時段(時段間隔,即SWMM的模擬步長,設置為1 s為宜),Qi為Si時段所對應的進水管出流量,q為所有泵的流量總和,qi為泵i的流量.只要保證Hmax與最高設計水位之間的體積V2不小于V1,即可確保水池的水位不會超過最高設計水位,即
V2=(HD-Hmax)×A≥V1.
(4)
式中HD為最高設計水位.結合式(2)和(4)整理得
(5)
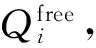

(6)
最終確定Hmax的計算方法為
(7)
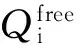
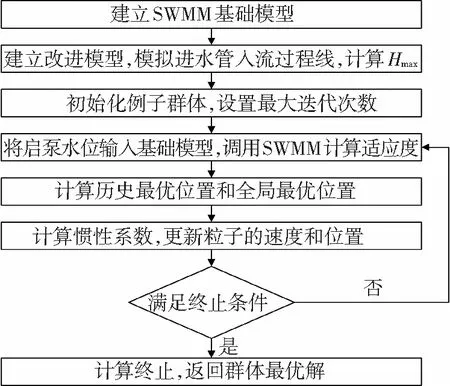
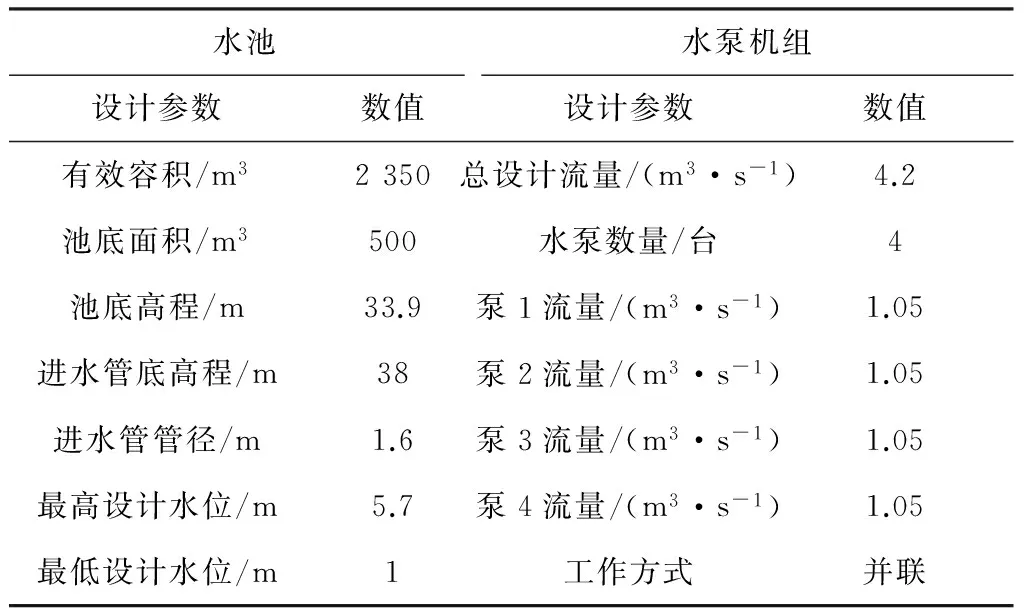
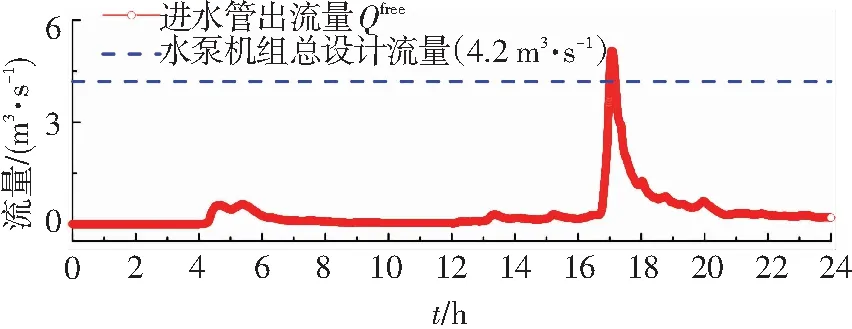
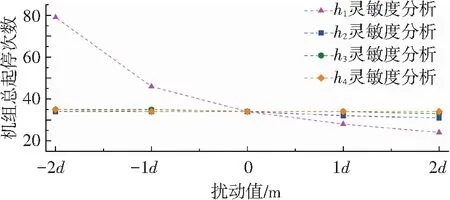
Hmin (8) 采用粒子群優化算法對目標函數進行優化計算.粒子群優化算法是較成熟的群體搜索優化算法,并已廣泛應用.該算法以粒子為單位,每個粒子具有多維度搜索空間,根據優化問題的評估方法來評價粒子適應度,進行粒子擇優.擇優后,所有粒子均朝向最優粒子的位置進行速度和位置更新,進而得到下一代群體.如此反復迭代計算,群體逐漸接近最優解,直到滿足終止條件為止[10-12]. 依據算法原理,在迭代計算之前首先要依據粒子維度,即需要優化的未知變量個數(本文為機組水泵總數),對粒子進行初始化.結合啟泵水位優化原理得粒子初始化公式為 (9) (10) (11) (12) wt=we(ws/we)1/(1+cNt/T). (13) 式中:ws和we分別為起始和終止時刻慣性系數,通常取ws=0.95和we=0.4,t為當前迭代次數,T為總迭代次數,cN為指數因子,通常取10.本文基于SWMM二次開發技術進行優化計算,步驟如下: 1)輸入降雨、管網、水池和水泵數據,建立SWMM基礎模型. 2)確定最大啟泵水位Hmax.將SWMM基礎模型中的水池替換為排水口得到改進模型,模擬并得到進水管出流過程線,依據式(7)計算Hmax. 3)初始化粒子群體.設置群體規模并根據機組水泵個數確定粒子維度.依據最低設計水位和步驟2)中獲得的Hmax,結合式(8)、(9)和(10)初始化所有粒子的速度和位置,生成初代群體. 4)計算適應度.將粒子的啟泵水位輸入到步驟1)的SWMM基礎模型中,調用SWMM計算引擎進行模擬計算.通過讀取模型結果計算式(1),得到粒子適應度. 5)計算歷史和全局最優位置.將粒子當前適應度與歷史最優解進行比較,得到該粒子的歷史最優位置.將所有粒子的歷史最優位置進行比較,得到群體的全局最優位置. 6)更新粒子群體.根據式(13)計算慣性系數.根據式(11)和(12)更新粒子的位置和速度,并判斷是否超出約束范圍.若超出,則重置到范圍內. 7)判斷是否滿足終止條件.若滿足,則終止計算,返回群體的全局最優位置;若不滿足,則返回步驟4). “以前我們進行課前學情調研,沒有想過為什么,因為區里或學校要求這樣,我們就這么去做了,還真沒有想過為什么,可能就是更加了解學生吧……” 算法的優化流程如圖3所示. 圖3 啟泵水位優化流程 3.1 實例一 采用人工調試方法對機組的啟泵水位進行人工調試優化.人工調試首先要確定調試參數的合理取值范圍,然后對參數進行靈敏度分析,明確參數調整方向及大小. 以某雨水泵站為例,該泵站建有一個調蓄池和一套水泵機組用于減少上游雨水管網的排水壓力.水池和水泵機組的設計參數如表1所示. 表1 水池和水泵設計參數 首先計算最高啟泵水位Hmax.當地設計重現期為10年一遇,因此依據以上設計參數和當地10年一遇的24 h設計降雨過程線,建立SWMM模型.設置模擬步長為1 s并模擬進水管為自由出流狀態下的出流過程線,如圖4所示. 圖4 進水管流量過程線 圖5 啟泵水位靈敏度分析 以啟泵水位為橫坐標,機組總啟停次數為縱坐標,進行線性回歸曲線擬合,各泵的啟泵水位擬合曲線斜率如表2所示.斜率的大小反應了參數的靈敏度,斜率的正負反應了總啟停次數變化方向.根據斜率值可以看出h1~h4的靈敏度逐漸減小,因此,在人工調試時應按照h1~h4的順序進行調試.以啟泵水位的基準值為初始值進行人工調試,其調試過程如表3所示. 表2 啟泵水位變化值的擬合斜率 表3 啟泵水位的人工調試過程 經過人工調試獲得最優啟泵水位如表3中的調試3.其中泵1~泵4的啟停次數分別為11次、1次、1次、1次.檢驗優化結果是否合理不僅要保證機組總啟停次數最少,還要將得到的啟泵水位輸入SWMM中模擬,保證滿足《室外排水規范》中提出的單個泵每小時啟停次數不超過6次以及水池的水位要始終低于最高設計水位.在4臺泵中只有泵1的啟停次數累計超過6次,因此,將人工調試結果輸入SWMM中模擬(考慮到管網匯流的滯后性,設置總模擬時長為36 h),并獲得泵1的流量過程和水池的水位過程如圖6和7所示.從圖6和7可以看出,泵1每小時啟停次數均在6次以內,水池的水位低于最高設計水位,滿足要求.可見,采用人工調試的方法將啟泵水位在合理的范圍內進行調整可以使啟停次數逐漸減少并最終得到一個較為理想的啟泵水位組合. 圖6 人工調試結果中泵1流量過程線 圖7 人工調試結果中水池水位過程線 3.2 實例二 運用本文優化算法對啟泵水位進行優化.各項設計參數、最高啟泵水位Hmax等輸入條件與實例一相同.設置粒子群體規模為20,優化迭代次數為50次.粒子速度的約束條件見式(14),根據式(9)和(10)始化粒子群體.進行迭代計算,得到水泵啟停次數和啟泵水位的優化計算過程如圖8和9所示. (14) 圖8 水泵啟停次數優化過程 圖9 啟泵水位優化過程 由圖8可以看出,隨著迭代次數增加,粒子適應度(水泵機組總啟停次數)不斷減小,在第23次迭代之后達到穩定.由圖9可以看出,泵1和泵2的啟泵水位不斷趨近于最優解,而泵3和泵4的啟泵水位在一定的波動之后達到穩定值.最終得到最優啟泵水位如表4所示. 表4 水泵機組運行參數優化結果 由表4可看出,只有泵1啟停次數累計超過6次.與實例一相同,將最優啟泵水位輸入SWMM進行模擬來驗證泵1每小時內的啟停次數和水池水位變化.泵1的流量過程線和水池的水位過程線如圖10和11. 圖10 泵1流量過程線 圖11 水池水位過程線 由圖10可以看出,泵1每小時的啟停次數均小于6次,圖11中水池的水位最高達到5.54 m,小于最高設計水位5.7 m.因此,運用優化算法得到的啟泵水位滿足要求,可以作為該泵站的啟泵水位進行設置. 對比實例一和實例二的優化過程,采用優化算法進行優化計算,無需工作人員有較多的調試經驗即可獲得較為合適的啟泵水位,并且在優化過程中避免了較多工作量的投入和對參數影響進行大量分析. 1)雨水泵站的啟泵水位如果設置不合理,會造成水泵啟停頻繁.通過人工調試的方法運用水力模型對啟泵水位進行反復調試,能夠獲得最佳啟泵水位使得水泵啟停次數滿足規范要求. 2)本文提出一種將優化算法與水力模型相結合的方法來優化啟泵水位.該方法通過構建啟泵水位優化模型,用SWMM對目標函數求解,進而得到最佳啟泵水位并使得啟停次數最少且滿足規范要求.優化得到的啟泵水位可以應用于雨水泵站,通過實例對此進行了驗證. 3)與人工調試方法相比,本文方法可以通過計算機自行優化計算,無需復雜的人工調試過程并且能夠獲得較好的啟停效果,可以指導啟泵水位的選取. [1] 張建新, 呂銳, 賀田富. 下穿式道路立交雨水泵站排水設計參數探討 [J]. 給水排水, 2012, 38(1): 30-35. DOI:10.13789/j.cnki.wwe1964.2012.01.019. ZHANG Jianxin, LV Rui, HE Tianfu. Probe into design parameters of undercrossing grade separation drainage system for rainwater pump station [J]. Water & Wastewater Engineering, 2012, 38(1): 30-35. DOI:10.13789/j.cnki.wwe1964.2012.01.019. [2] 劉瀾, 王峰, 李楊秋,等. 廈門機場路雨水泵站調蓄優化設計 [J]. 給水排水, 2009, 35(5): 50-52. LIU Lan, WANG Feng, LI Yangqiu, et al. Optimization design of water pump station in Xiamen Airport Road [J]. Water & Wastewater Engineering, 2009, 35(5): 50-52. [3] 孫艷濤. 下穿鐵路立交橋排水泵站設計及安全防護 [J]. 給水排水, 2015, 41(4): 45-47. DOI: 10.13789/j.cnki.wwe1964.2015.0123. SUN Yantao. Design and safety protection of drainage pumping station under interchange [J]. Water & Wastewater Engineering, 2015, 41(4): 45-47. DOI: 10.13789/j.cnki.wwe1964.2015.0123. [4] 郭磊,姚雙龍,李玢,等. 基于水力模型的下凹式立交橋橋區雨水泵站運行優化 [J]. 給水排水, 2014, 40(3): 102-104. DOI: 10.13789/j.cnki.wwe1964.2014.0025. GUO Lei, YAO Shuanglong, LI Bin, et al. Concave-down overpass rainwater pump station operation optimization based on hydraulic model [J]. Water & Wastewater Engineering, 2014, 40(3): 102-104. DOI: 10.13789/j.cnki.wwe1964.2014.0025. [5] 王彤,劉志強,李曉娜,等.城市雨水泵站運行效果模擬及優化調控分析[J]. 水電能源科學, 2016, 34(3):181-184. WANG Tong, LIU Zhiqiang, LI Xiaona, et al. Simulation and optimization analysis of urban storm water pump station operation [J]. Water Resources and Power, 2016, 34(3):181-184. [6] 中華人民共和國建設部. 室外排水設計規范: GB 50014—2006 [S]. 北京: 中國計劃出版社, 2014: 45-50. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for design outdoor wastewater engineering: GB 50014—2006 [S]. Beijing: China Planning Press, 2014: 45-50. [7] 俞鋒. 城鎮排水泵站集水池設計水位的確定 [J]. 浙江建筑, 2011, 28(6): 54-56. DOI: 10.15874/j.cnki.cn33-1102/tu.2011.06.016. YU Feng. Determination of the collection basin design water level of drainage pumping station [J]. Zhejiang Construction, 2011, 28(6): 54-56. DOI: 10.15874/j.cnki.cn33-1102/tu.2011.06.016. [8] 劉猛, 陶月贊, 郭增輝. 下穿既有鐵路線立交橋雨水泵站設計 [J]. 工程建設與設計, 2011(3):111-114. LIU Meng, TAO Yuezan, GUO Zenghui. Design of overpass rainwater pump station in crossing existing railway [J]. Construction & Design for Project, 2011(3):111-114. [9] 劉欣. 城市排水泵站的優化運行管理 [D]. 天津: 天津大學環境學院, 2011: 21-36. LIU Xin. Optimization of operation and regulation of urban drainage pump station [D]. Tianjin: TianjinUniversity, College of the Environment, 2011: 21-36. [10]LI Yuhua, ZHAN Zhihui, LIN Shujin, et al. Competitive and cooperative particle swarm optimization with information sharing mechanism for global optimization problems [J]. Information Sciences, 2015, 293: 370-382. DIO: 10.1016/j.ins.2014.09.030. [11]ASHTIANI E F, NIKSOKHAN M H, ARDESTANI M. Multi-objective waste load allocation in river system by MOPSO algorithm [J]. International Journal of Environmental Research, 2015, 9(1): 69-76. [12]GHOSHAL S P. Optimizations of PID gains by particle swarm optimizations in fuzzy based automatic generation control [J]. Electric Power Systems Research, 2004, 72(3): 203-212. [13]MENDONCA I M, SILVA I C, MARCATO A L M. Static planning of the expansion of electrical energy transmission systems using particle swarm optimization[J]. International Journal of Electrical Power & Energy Systems, 2014, 60: 234-244. [14]JIANG Yan, LI Xuyong, HUANG Chongchao. Automatic calibration a hydrological model using a master-slave swarms shuffling evolution algorithm based on self-adaptive particle swarm optimization [J]. Expert Systems with Applications, 2013, 40(2): 752-757. DOI: 10.1016/j.eswa.2012.08.006. [15]YANG Wen’an, ZHOU Wei, LIAO Wenhe, et al. Prediction of drill flank wear using ensemble of co-evolutionary particle swarm optimization based-selective neural network ensembles [J]. Journal of Intelligent Manufacturing, 2016, 27(2): 343-361. DOI: 10.1007/s10845-013-0867-2. [16]JIANG Yan, LIU Changmin, HUANG Chongchao, et al. Improved particle swarm algorithm for hydrological parameter optimization [J]. Applied Mathematics and Computation, 2010, 217(7): 3207-3215. DOI: 10.1016/j.amc.2010.08.053. [17]SHI Y, EBERHART R. Empirical study of particle swarm optimization [ C ] // Proceeding of the 1999 Congress on Evolutionary Computation. Washington: IEEE, 1999: 1945-1950. (編輯 劉 彤) Optimization of pump start-stops in rainwater pump station WANG Hao1,2,ZHANG Yongxiang1,2, TANG Ying1,2,LIU Yu1,2,LI Kaixuan1,2 (1.College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China; 2.Key Laboratory of Beijing for Water Quality Science and Water Environment Recovery Engineering(Beijing University of Technology), Beijing 100124, China) A pump start-stops optimization method was proposed to realize the frequent start-stops in rainwater pump station. Through analyzing the design parameters and operation principles, the optimization model of pump start water level was obtained by SWMM(storm water management model) and PSO(particle swarm optimization algorithm). The feasibility of the optimization method was verified by comparing with manual debugging method. The research results show that the optimization method can minimize the start-stop frequency, achieve a better effect of bump start-stops and get rid of the complex manual debugging process, which will provide reference for the pumping water level selection of rainwater pumping stations. rainwater pump station; start-up optimization; storm water management model (SWMM); particle swarm optimization algorithm (PSO); optimal pump start water level 10.11918/j.issn.0367-6234.201609076 2016-09-20 國家科技支撐計劃項目(2011BAC12B00) 王 昊(1987—),男,博士研究生; 張永祥(1962—),男,教授,博士生導師 王 昊,15801646483@163.com TU992 A 0367-6234(2017)08-0098-062 優化方法的實現

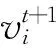

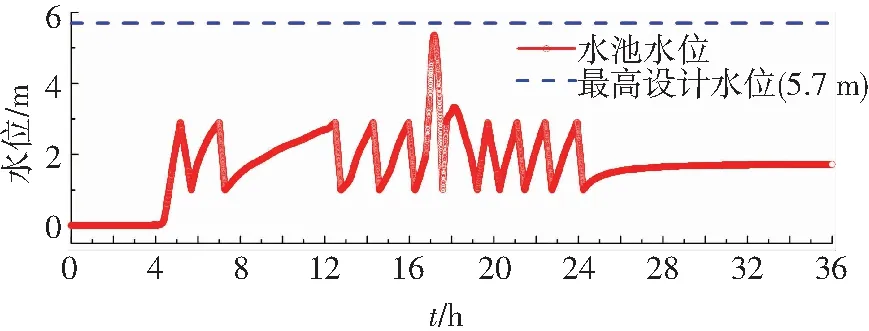
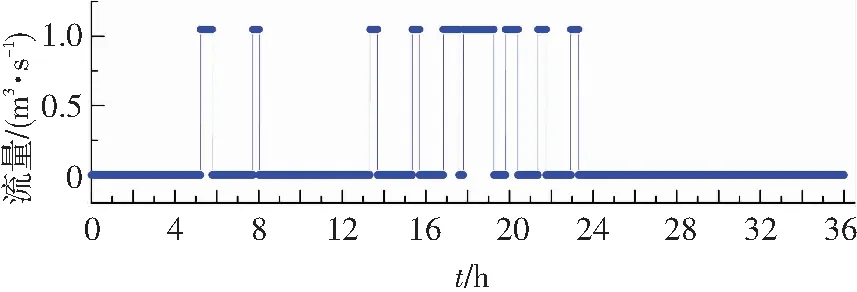
3 實例研究







4 結 論

