非匹配不確定的彈性高超聲速飛行器終端滑模控制

宗 群，張秀云，邵士凱，葉林奇，董 琦

(天津大學 電氣自動化與信息工程學院,天津 300072)

非匹配不確定的彈性高超聲速飛行器終端滑模控制

宗 群，張秀云，邵士凱，葉林奇，董 琦

(天津大學 電氣自動化與信息工程學院,天津 300072)

為解決帶有非匹配不確定的彈性高超聲速飛行器(FHV)魯棒跟蹤控制問題，設計一種基于有限時間干擾觀測器的非奇異終端滑模控制器.首先，通過將彈性模態的影響視為不確定，與系統參數不確定一起處理為綜合不確定，將帶有彈性的高超聲速飛行器模型簡化為便于控制器設計的面向控制模型；其次，設計有限時間干擾觀測器估計模型的綜合不確定；進而，基于干擾觀測器，設計一種新型的非奇異終端滑模面，將高階不匹配問題轉化成一階匹配問題，進行控制器的設計;最后通過Lyapunov理論證明了閉環系統的穩定性.仿真結果表明：所設計的控制器可以有效抑制非匹配不確定及彈性的影響，實現了飛行器速度與高度的穩定跟蹤控制.

控制；高超聲速飛行器；非匹配不確定；有限時間干擾觀測器；非奇異終端滑模

高超聲速飛行器一般指飛行馬赫數大于5的飛行器，在軍事和民用上具有巨大的應用價值.近年來，世界各國都把探索與發展高超聲速技術作為航空航天領域的一個重要目標，掀起了研究和發展高超聲速飛行器的熱潮.高超聲速飛行器所具有的高速度、強非線性、強耦合性、強不確定(隨機干擾引起的不確定及彈性形變引起的不確定等)等一系列特性，都給控制上帶來了極大的挑戰.

高超聲速飛行器彈性問題的存在，導致彈性狀態與剛體狀態之間產生強烈的耦合，給飛行器的控制帶來了極大的困難.因此，如何解決彈性影響下的高超聲速飛行器控制是控制的難點問題.另外，模型不確定問題也是飛行器控制中的一大難點，不確定分為匹配不確定與非匹配不確定.所謂匹配不確定是指不確定出現在輸入通道中，反之則為非匹配不確定.解決非匹配不確定問題最常用的方法為反步控制[1]，然而單純的反步控制會導致所謂的“計算爆炸”問題.除反步控制外，滑模方法對模型不確定及外部干擾具有強魯棒性，得到廣泛應用.但傳統滑模控制方法只能解決匹配不確定問題，因此，一方面，通過將滑模方法與反步控制方法結合使用[2-3]，使得兩者的優勢相互結合，達到更好的控制效果.另一方面，隨著Levant等人[4]提出干擾觀測器的概念，作為對非線性系統中的外界干擾和不確定估計的有效手段，成為了研究的熱點[5-7].除傳統滑模外，高階滑模控制也得到廣泛的應用[8-9].文獻[10]利用反饋線性化后的高超聲速飛行器模型，設計觀測器實現對系統未知狀態的估計，并設計滑模控制器保證整個閉環系統的穩定性.如何單獨利用滑模方法，基于非線性控制系統設計控制器，解決非匹配不確定問題是一個研究難點.文獻[11]針對一般的帶有非匹配干擾的系統，設計了基于有限時間干擾觀測器的連續非奇異終端滑模面，解決了非匹配干擾問題，并應用于永磁同步電機的控制上.

本文受到文獻[11]的啟發，通過設計一種新型終端滑模面，將高超聲速飛行器高階非匹配問題轉化為一階匹配問題，簡單有效地處理飛行器的非匹配不確定問題.

1 模型描述

本文考慮的吸氣式高超聲速飛行器縱向動力學模型來源于文獻[12]的研究成果.基于平面地球假設，將飛行器建模為一個彈性結構，推導的運動方程中包含彈性效應，同時剛體動力學和彈性動力學之間通過氣動力產生耦合.高超聲速飛行器縱向動力學模型為

(1)

(2)

(3)

式中參數具體取值見文獻[13].

由于縱向動力學模型(1)～(3)的強耦合、強不確定等特性，不適合直接進行控制器設計，因此通過將彈性與剛體之間的耦合視為綜合不確定，并經過進一步的調整，可得到面向控制模型[14]為

(4)

式中:eγ為航跡角γ及其期望值γr之間的誤差，記為eγ=γ-γr；ΔV,Δγ,Δq為綜合不確定變量，其中Δγ為非匹配不確定,ΔV,Δq為匹配不確定；另外，其他系數表達為

高超聲速飛行器控制的目標是設計控制器φ,δe，使得飛行器的速度V與高度h沿著給定的參考軌跡Vr,hr飛行，保證跟蹤誤差在有限時間內趨于0.后續控制器設計過程中會將飛行器模型(4)分為速度環與高度環，基于多時間尺度理論，分別進行控制器設計.

2 基于自適應律的速度環控制器設計

由于本文采用的基于有限時間干擾觀測器的新型非奇異終端滑模方法主要針對非匹配不確定問題，而速度環為一階系統，并不存在非匹配不確定問題，故此處速度環采用自適應滑模方法進行控制器的設計.

由式(4)知，速度環模型為

φ+ΔV.

(5)

定義速度跟蹤誤差為

eV=V-Vr.

(6)

對式(6)進行求導并代入式(5)，可得到速度跟蹤誤差動態為

(7)

控制量設計為

(8)

).

(9)

式中μ為大于0的常數，κ為待設計參數.

引理1[16]針對系統

(10)

式中z為狀態量，f(z)為已知連續函數.假設存在一個連續可微的正定函數Ψ(z):D→Rn,λ>0,0<τ<1,0<ψ<,使得成立，則系統(10)是實際有限時間穩定的，且到達時間為

(11)

其中Ψ(z0)為Ψ(z)的初始值.

定理1 在假設1的條件下，針對速度環動力學模型(5)，選取合適的參數，則利用基于綜合不確定自適應律估計(9)的控制輸入(8)能夠保證速度跟蹤誤差(6)在有限時間內收斂到原點的任意小的ε-鄰域內，定義Lyapunov函數

(12)

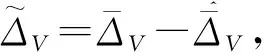
(13)

式中0<θ0<1，Vv(0)為Vv(x)的初始值.

(14)

對Lyapunov函數(12)進行求導，可以得到

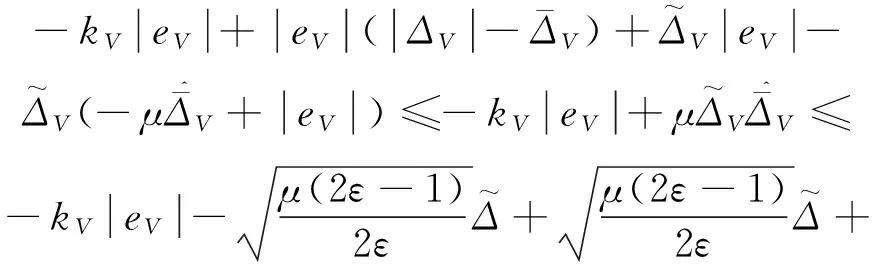
(15)

(16)

因此，式(15)轉化為

(17)

根據假設1，ΔV是有界的，根據引理1可知，速度跟蹤誤差(6)是有限時間收斂的，且收斂時間為

(18)

3 基于有限時間干擾觀測器的高度環控制器設計

定義高度跟蹤誤差為

eh=h-hr.

由于航跡角γ很小，因此假設sinγ≈γ.對式(18)進行求導，得到

(19)

虛擬控制量γr設計為

(20)

式中kh1,kh2>0，0<ρ<1.

定義跟蹤誤差為eγ=γ-γr，將式(20)代入式(19)可得

(21)

因此只需eγ→0，則有eh→0，下面將設計非奇異終端滑模控制器,使得eγ→0.

為了便于后文書寫方便，定義[x1,x2,x3]=[eγ,θ,Q],[d1,d2]=[Δγ,Δq].根據式(4)，eγ,θ,Q的狀態方程變為

(22)

從式(22)中可以看出，d1為非匹配不確定，d2與控制輸入在一個通道，為匹配不確定.

[11]，針對式(22)設計一種新型的滑模面，首先定義擴展狀態變量為

(23)

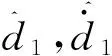
(24)

(25)

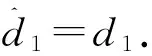
設計如下非奇異終端滑模面

(26)

式中ki,αi(i=1,2,3)為大于0的常數.

對滑模面(26)進行求導，得到

(27)

設計控制器為

(28)

定理2 針對系統(22)，若假設1成立，且參數選取恰當，則有限時間干擾觀測器估計誤差會在有限時間內趨于0，并且在控制律(28)作用下，滑模面(26)會有限時間內收斂，從而使得高度跟蹤誤差(18)有限時間內收斂至0.

證明 將控制器(28)代入式(27)中，得到

(29)

另外對式(23)求導，并將式(28)代入式(23)可以得到

(30)

(31)

對式(31)進行求導，得到

(32)

當干擾估計誤差在有限時間內收斂到0以后，滑模動態(29)變為

(33)

(34)

該系統是有限時間收斂的[19].

4 仿真分析

為了說明所設計控制器的有效性，下面將進行MATLAB仿真分析.

4.1 仿真條件及參數設置

針對飛行器機動爬升階段，給定的飛行器速度的參考軌跡為由初始速度2 350 m/s經過二階濾波器，自然頻率為0.06 rad/s，阻尼為0.95，實現階躍變化量ΔV=30.5 m/s，高度的參考軌跡為25 925 m經過同樣的濾波器實現階躍變化量Δh=610 m .控制器中參數設置分別為：k1=k2=15,k3=5，kv=3，kh1=kh2=2，ρ=0.5，K1=5,K2=0.5，α1=α2=0.65，α3=1.3，κ=2，μ=6.有限時間干擾觀測器參數設置為：λ0=λ1=3，λ2=2，L1=L2=5.

4.2 仿真結果分析

在上述仿真條件下，分別利用本文的新型終端滑模及反步控制方法，完成FHV縱向爬行機動仿真實驗.其仿真結果如圖1～5所示.

從仿真結果圖1可以看出，兩種方法均可實現非匹配不確定下高超聲速飛行器速度與高度的穩定有效跟蹤，但本文方法可以在有限時間內達到跟蹤效果.當飛行器進入穩定狀態后，從圖2、3可以看到，控制量與其他狀態量均可以趨于穩態值，有效的抑制了彈性及不確定的影響.圖4、5表明，干擾觀測器的估計誤差及速度與高度滑模面均可以在有限時間內可以收斂到0.

圖1 飛行器速度及高度曲線

圖2 控制量變化曲線

圖3 其余狀態量變化曲線

圖4 觀測器估計誤差變化曲線

圖5 滑模面變化曲線

5 結 論

1)針對帶彈性的高超聲速飛行器的非匹配不確定問題，采用了一種基于有限時間干擾觀測器的非奇異終端滑模控制策略，巧妙地在滑模面設計中加入了非匹配不確定的估計值，從而抵消其對系統穩定性的影響.

2)該方法可以將高階非匹配問題轉化成一階匹配問題，計算簡單，有效地解決了非匹配不確定問題.且仿真結果表明，該方法設計的控制器可以實現速度與高度的有限時間穩定跟蹤.

參考文獻

[1] BU Xiangwei, WU Xiaoyan, YONG Yongxing, et al. Tracking differentiator design for the robust backstepping control of a flexible air-breathing hypersonic vehicle[J]. Journal of the Franklin Institute, 2015, 352(4): 1739-1765. DOI: 10.1016/j.jfranklin.2015.01.014.

[2] GINOYA D, SHENDGE P D, PHADKE S B. Disturbance observer based sliding mode control of nonlinear mismatched uncertain systems[J]. Communications in Nonlinear Science and Numerical Simulation, 2015，26(1/2/3): 98-107. DOI: 10.1016/j.cnsns.2015.02.008.

[3] MONDAL S, MAHANTA C. Chattering free adaptive multivariable sliding mode controller for systems with matched and mismatched uncertainty[J]. ISA Transactions, 2013, 52(3): 335-341. DOI: 10.1016/j.isatra.2012.12.007.

[4] SHTESSEL Y B, SHKOLNIKOV I A, LEVANT A. Smooth second-order sliding modes: missile guidance application[J]. Automatica, 2007, 43(8): 1470-1476. DOI: 10.1016/j.automatica.2007.01.008.

[5] SUN Haibin, GUO Lei. Composite adaptive disturbance observer based control and back-stepping method for nonlinear system with multiple mismatched disturbances[J]. Journal of the Franklin Institute, 2014, 351(2): 1027-1041.DOI:10.1016/j.jfranklin.2013.10.002.

[6] SUN Haibin, LI Shihua, YANG Jun, et al. Non-linear disturbance observer-based back-stepping control for airbreathing hypersonic vehicles with mismatched disturbances[J]. IET Control Theory and Applications, 2014, 8(17): 1852-1865. DOI: 10.1049/iet-cta.2013.0821.

[7] WANG Na, WU Huaining, GUO Lei. Coupling-observer-based nonlinear control for flexible air-breathing hypersonic vehicles[J]. Nonlinear Dynamics, 2014, 78(3): 2141-2159. DOI: 10.1007/s11071-014-1572-1.

[8] WANG Jie, ZONG Qun, TIAN Bailing, et al. Flight control for a flexible air-breathing hypersonic vehicle based on quasi-continuous high-order sliding mode[J]. Journal of Systems Engineering and Electronics, 2013, 24(2): 288-295.DOI:10.1109/JSEE.2013.00036.

[9] 宗群，蘇芮，王婕，等. 高超聲速飛行器自適應高階終端滑模控制[J]. 天津大學學報(自然科學與工程技術版)，2016,47(11):1031-1037.DOI: 10.11784/tdxbz201309014.

ZONG Qun, SU Rui, WANG Jie, et al. Adaptive high-order terminal sliding mode control for hypersonic flight vehicle[J]. Journal of Tianjin University(Science and Technology), 2016,47(11):1031-1037. DOI: 10.11784/tdxbz201309014.

[10]MU Chaoxu, SUN Changyin, YU Xinghuo. Observation and control for air-breathing hypersonic aircrafts based on sliding mode method[C]// Conference on IEEE Industrial Electronics Society. Melbourne: IEEE Press, 2011:3965-3970.DOI: 10.1109/IECON.2011.6119957.

[11]YANG Jun, LI Shihua, SU Jinya, et al. Continuous nonsingular terminal sliding mode control for systems with mismatched disturbances[J]. Automatica, 2013, 49(7): 2287-2291. DOI: 10.1016/j.automatica.2013.03.026.

[12]FIORENTINI L. Nonlinear adaptive controller design for air-breathing hypersonic vehicles[D]. Columbus: The Ohio State University, 2010.

[13]YE Linqi, ZONG Qun, ZHANG Xiuyun. Adaptive control for a non-minimum phase hypersonic vehicle model[C]//2015 34th Chinese Control Conference (CCC). Hangzhou: IEEE Press, 2015: 991-996.DOI: 10.1109/ChiCC.2015.7259769.

[14]ZONG Qun, WANG Fang, TIAN Bailing, et al. Robust adaptive dynamic surface control design for a flexible air-breathing hypersonic vehicle with input constraints and uncertainty[J]. Nonlinear Dynamics, 2014, 78(1):289-315. DOI: 10.1007/s11071-014-1440-z.

[15]ZHU Zheng, XIA Yuanqing, FU Mengyin. Attitude stabilization of rigid spacecraft with finite-time convergence[J]. International Journal of Robust and Nonlinear Control, 2011, 21(6): 686-702. DOI: 10.1002/rnc.1624.

[16]TIAN Bailing, SU Rui, FAN Wenru. Multiple-time scale smooth second order sliding mode controller design for flexible hypersonic vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2014: 0954410014539466. DOI: 10.1177/0954410014539466.[17]LI Shihua, TIAN Y P. Finite-time stability of cascaded time-varying systems[J]. International Journal of Control, 2007, 80(4): 646-657. DOI: 10.1080/00207170601148291.

[18]BHAT S P, BERNSTEIN D S. Finite-time stability of continuous autonomous systems[J]. SIAM J on Control and Optimization, 2000, 38(3): 751-766. DOI: 10.1137/S0363012997321358.

[19]BHAT S P, BERNSTEIN D S. Geometric homogeneity with applications to finite-time stability[J]. Mathematics of Control, Signals and Systems, 2005, 17(2): 101-127. DOI: 10.1007/s00498-005-0151-x.

(編輯 魏希柱)

Terminal sliding mode control for flexible hypersonic vehicle with mismatched uncertainties

ZONG Qun, ZHANG Xiuyun, SHAO Shikai, YE Linqi, DONG Qi

(School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China)

A finite-time disturbance observer-based nonsingular terminal sliding mode control strategy is proposed for flexible hypersonic vehicle (FHV) with mismatched uncertainties. First of all, by considering the effects of flexible modes as uncertainties, the control-oriented model, which is convenient for controller design, is obtained by simplification of the FHV model. Then, the lumped uncertainties are estimated by finite-time disturbance observer. Afterwards, a novel nonsingular terminal sliding surface containing the disturbance estimations is designed, which can transform the high-order mismatched uncertainties into first-order matched uncertainties. Then the controller is developed. The stability of the closed-loop system is guaranteed by Lyapunov theory. Simulation results show that the proposed controller is effective in suppressing the mismatched uncertainties and has achieved stable tracking of velocity and altitude.

control; hypersonic vehicle; mismatched uncertainties; finite-time disturbance observer; nonsingular terminal sliding mode

10.11918/j.issn.0367-6234.201610118

2016-10-29

國家自然科學基金(61673294，61273092)

宗 群(1961—)，男，教授，博士生導師

邵士凱，kdssk@126.com

TP273

A

0367-6234(2017)08-0158-07