王永茂， 李 丹， 魏 靜

(燕山大學 理學院 河北 秦皇島 066004)

隨機利率下基于Tsallis熵及O-U過程的冪式期權定價

王永茂， 李 丹， 魏 靜

(燕山大學 理學院 河北 秦皇島 066004)

為了準確描述股票價格的變化規律，對經典的Black-Scholes期權定價模型進行改進，利用具有尖峰厚尾和長期相依特征的Tsallis熵分布、具有均值回復性的O-U過程，建立股票價格的變化模型，在無風險利率服從Vasicek模型下，運用隨機微分和等價鞅測度的方法得到了冪式期權的定價公式，推廣了經典的Black-Scholes定價理論，擴展了已有文獻的結論.

Tsallis熵； Vasicek模型； O-U過程； 鞅

0 引言

1973年發表的Black-Sholes期權定價模型[1]是期權定價理論的基礎，但是B-S模型的假設過于嚴格，它假設股票價格服從幾何布朗運動.幾何布朗運動刻畫的資產價格運行模式意味著資產價格變化是相互獨立的隨機變量，收益率服從正態分布而且不具有歷史記憶性.然而，近年來國內外大量研究表明，資產收益率的分布具有尖峰厚尾的現象和長期相依的性質[2].另外，從長期來看，資產價格的變化有回到其長期平均值的傾向，不少學者采用具有均值回復性的O-U過程來刻畫資產價格的變化規律，如文獻[3]利用精算方法得到了O-U過程的歐式期權的定價公式.

文獻[4]提出了非廣延Tsallis熵理論.Tsallis熵分布可以用來描述具有非線性、長程相互作用和長期記憶效應的復雜系統.文獻[5]利用Tsallis熵分布對不同國家的股票收益率進行研究，得知Tsallis熵分布可較好的擬合股票的收益率分布. 文獻[6]利用Tsallis熵理論對我國股市進行了研究，得知我國股市的價格過程并不符合隨機游走，而是服從反常擴散過程，具有明顯的非線性動力系統特征.

考慮到在現實的金融市場中，利率在短時間內往往表現出一定的隨機性，但長遠來看，其變化有向均衡水平靠攏的趨勢，故本文在傳統期權定價研究方法的基礎上，采用Vasicek模型來刻畫利率的變化規律，用最大化Tsallis熵分布和O-U過程來刻畫股票價格的變化規律，運用等價鞅測度方法，研究了風險環境下冪式期權的定價問題.

1 股票價格模型

考慮一個連續時間的無摩擦金融市場，假設市場上存在兩種可交易金融資產：一種是無風險債券；另一種是風險資產股票.假設在t時刻的股票價格S(t)滿足隨機微分方程

dS(t)=(μ-blnS(t))S(t)dt+σ1S(t)dΩ(t)，

(1)

該概率密度函數P(Ω,t)滿足非線性Fokker-Planck方程[7]

其對應微觀尺度下的Ito-Langevin方程為

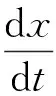
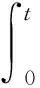
(2)

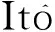
故在概率測度Q下，S*(t)為鞅.

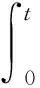
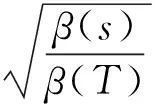
2 利率模型

在等價鞅測度Q下，市場為風險中性，此時假設利率r(t)服從Vasicek模型，即滿足隨機微分方程

dr(t)=a(θ-r(t))dt+σ2dBQ(t),r(0)=r0,

(3)

其中:{BQ(t)：0≤t≤T}是Q上的標準布朗運動，與{WQ(t)：0≤t≤T}獨立；θ為常數，表示長期均衡的利率水平；a為調整短期和長期利率關系的平均回復率；σ2為利率的波動率.

引理4[8]若隨機利率r(t)服從Vasicek模型，即滿足隨機微分方程(3)，則有

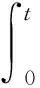
(4)

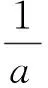
3 冪式期權定價

本文研究的冪式期權形式如下：

定理1 若股票價格S(t)滿足隨機微分方程(1)，隨機利率服從Vasicek模型(3)，且股票無紅利支付，則到期日為T. 執行價格為K的冪式看漲及看跌期權在0時刻的價格分別為：

(5)

(6)

其中:

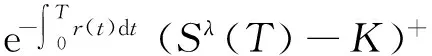
引理2中的(2)式取對數，同時將(4)式代入可得到期權執行的充要條件S(T)>K，等價于

(7)

由引理3可得

(8)

(9)

將式(8)和(9)代入(7)式可得期權執行的充要條件為

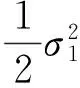
所以有:

對上述兩式相減則可得冪式看漲期權定價式(5)，同理可得該模型下冪式看跌期權的定價公式(6).

注 1) 當q=1,b=0,λ=1時，由定理1可得Vasicek利率模型下經典B-S模型的歐式期權定價公式.

2) 當b=0,λ=1時，由定理1可得Vasicek利率模型下基于最大化Tsallis熵的歐式期權定價公式.

3) 當q=1,λ=1時，由定理1可得Vasicek利率模型下基于O-U過程的歐式期權定價公式.

4 結束語

文章對傳統期權定價模型進行改進，結合具有長程記憶及統計反饋性質的Tsallis熵分布和具有均值回復特征的O-U過程，通過等價鞅測度方法，得出了Vasicek隨機利率模型下的冪式期權定價公式.與文獻[8]和文獻[9]的結論相比，本文結論綜合考慮了Tsallis熵、O-U過程和隨機利率對期權定價的影響，豐富了期權定價的相關結論.

[1] BLACK F，SCHOLES M．The pricing of options and corporate liabilities[J]．Journal of political economy，1973，81(3)：133-155.

[2] 陳倩，李金林，張倫．基于g-h分布的上證指數收益率分布擬合研究[J]．中國管理科學，2008，16：226-230.

[3] 閆海峰，劉三陽．股票價格遵循Ornstein-Uhlenback過程的期權定價[J]．系統過程學報，2003，18(6)：547-551.

[4] TSALLIS C．Possible generalization of Boltzmann-Gibbsstatistics[J]．Journal of statistical physics，1988，52(1)：479-487.

[5] MICHAEL F，JOHNSON M D．Financial market dynamics[J]．Physica A： statistical mechanics and its applications，2003，320(c)：525-534.

[6] 張磊，茍小菊．基于Tsallis理論的中國股市收益分布研究[J]．運籌與管理，2012，21(3)：200-205.

[7] BORLAND L．A theory of non-Gaussian option pricing [J]．Quantitative finance，2007，2(6)：415-431.

[8] 趙攀，肖慶憲．隨機利率下基于O-U過程的冪型歐式期權定價[J]．合肥工業大學學報(自然科學版)，2014，37(11)：1386-1390.

[9] 趙攀，肖慶憲．基于Tsallis分布的歐式期權定價[J]．系統工程，2015，33(1)：18-23．

(責任編輯：方惠敏)

Pricing of Power European Options Based on Tsallis Entropy and O-U Process under Stochastic Interest Rate

WANG Yongmao， LI Dan， WEI Jing

(CollegeofScience，YanshanUniversity，Qinhuangdao066004，China)

The classical Black-Scholes option pricing model was improved in order to accurately describe the fluctuation of stock price.Thus, the distribution of Tsallis entropy, which had fat-tailed and long-term dependent characteristics,and O-U process were selected to describe the law of the stock prices fluctuation. By using the stochastic differential and martingale under the Vasicek interest rate model, the pricing formulas of power European options were obtained. The formulas not only generalized the classical Black-Scholes conclusion, but also corroborated the conclusions in the other literature.

Tsallis entropy； Vasicek interest rate model； O-U process； martingale

2016-10-09

廊坊市科技局科學技術研究項目(2016011031)．

王永茂(1958—)，男，河北秦皇島人，教授，主要從事壽險精算、概率論研究；通信作者：李丹(1989—)，女，山西運城人，主要從事保險定價理論研究，E-mail:245514309@qq.com.

O211.6；F830.9

A

1671-6841(2017)03-0001-04

10.13705/j.issn.1671-6841.2016261