復(fù)雜網(wǎng)絡(luò)譜粗粒化方法的改進算法?

周建 賈貞?李科贊

1)(桂林理工大學(xué)理學(xué)院,桂林 541004)

2)(桂林電子科技大學(xué)數(shù)學(xué)與計算科學(xué)學(xué)院,桂林 541004)

(2016年10月2日收到;2016年11月21日收到修改稿)

復(fù)雜網(wǎng)絡(luò)譜粗粒化方法的改進算法?

周建1)賈貞1)?李科贊2)

1)(桂林理工大學(xué)理學(xué)院,桂林 541004)

2)(桂林電子科技大學(xué)數(shù)學(xué)與計算科學(xué)學(xué)院,桂林 541004)

(2016年10月2日收到;2016年11月21日收到修改稿)

大規(guī)模網(wǎng)絡(luò)的同步問題是網(wǎng)絡(luò)科學(xué)的重要研究課題之一.粗粒化方法提供了一種將大規(guī)模網(wǎng)絡(luò)轉(zhuǎn)化為小規(guī)模網(wǎng)絡(luò),同時又能較好地保持原始網(wǎng)絡(luò)的拓撲性質(zhì)或動態(tài)特性的研究途徑,其中比較有代表性的譜粗粒化方法能較好地保持初始網(wǎng)絡(luò)的同步能力.然而,譜粗粒化方法在實際計算中計算量大、對實際大規(guī)模網(wǎng)絡(luò)可執(zhí)行性差.本文提出一種改進的譜粗粒化算法,能大幅減少計算量,同時獲得更好的譜粗粒化效果.通過理論分析和大量的數(shù)值仿真實驗驗證了所提改進算法的粗粒化效果和計算量都明顯優(yōu)于原譜粗粒化方法.

復(fù)雜網(wǎng)絡(luò),同步,譜粗粒化,改進算法

1 引 言

同步是自然界、人類社會和工程技術(shù)領(lǐng)域中一種常見的集合運動現(xiàn)象,如蛙聲齊鳴、有節(jié)律的鼓掌等.近二十多年來,研究人員對復(fù)雜動態(tài)網(wǎng)絡(luò)的同步進行了大量研究,特別是對于中尺度網(wǎng)絡(luò)的同步研究取得了豐富的研究成果[1?11].然而,許多實際網(wǎng)絡(luò)是擁有成千上萬甚至上億節(jié)點的大規(guī)模網(wǎng)絡(luò),研究大規(guī)模耦合復(fù)雜動態(tài)網(wǎng)絡(luò)同步常常會產(chǎn)生大量的耦合微分方程,給計算和仿真實驗都帶來巨大困難,許多中尺度網(wǎng)絡(luò)同步算法在大規(guī)模網(wǎng)絡(luò)研究中難以實現(xiàn),因此人們提出了一些粗粒化方法試圖將大規(guī)模網(wǎng)絡(luò)轉(zhuǎn)化為中尺度網(wǎng)絡(luò)來研究[12?17].粗粒化方法通過合并相似節(jié)點將大規(guī)模網(wǎng)絡(luò)縮減為中尺度網(wǎng)絡(luò),同時盡量保持原始網(wǎng)絡(luò)的某些重要性質(zhì),如拓撲特性或動力學(xué)性質(zhì)等.近年來,在粗粒化的研究方面也取得了一些重要進展.例如, K im[18]提出了一種粗粒化方法能保持原始網(wǎng)絡(luò)的度分布、聚類系數(shù)、同配系數(shù)等性質(zhì);Chen等[19]提出了一種基于網(wǎng)絡(luò)度的粗粒化方法,能保持原始網(wǎng)絡(luò)平衡態(tài)統(tǒng)計分布的一致性.在這些粗粒化方法中,比較典型的是由G feller和Rios[20,21]在2008年提出的譜粗粒化(spectral coarse graining,SCG)方法,通過分析網(wǎng)絡(luò)結(jié)構(gòu)矩陣的特征值譜,合并網(wǎng)絡(luò)中結(jié)構(gòu)相同和相似的節(jié)點,從而有效地將大規(guī)模網(wǎng)絡(luò)縮減為小規(guī)模網(wǎng)絡(luò)同時又能較好地保持初始網(wǎng)絡(luò)的同步能力.Chen等[15]進一步研究了SCG方法在聚類網(wǎng)絡(luò)中的應(yīng)用效果,Zeng和Lü[16]進一步提出了基于有向網(wǎng)絡(luò)的SCG方法,能很好地保持粗粒化網(wǎng)絡(luò)的同步能力.

SCG方法在保持網(wǎng)絡(luò)同步能力方面獨占優(yōu)勢,然而在確定網(wǎng)絡(luò)中的哪些節(jié)點被合并時需要反復(fù)判斷,這樣會產(chǎn)生非常巨大的計算量,其計算復(fù)雜度為O(N3)[16].對于現(xiàn)實中少則成千上萬節(jié)點的網(wǎng)絡(luò),多則上百萬甚至上億節(jié)點的大規(guī)模網(wǎng)絡(luò),其巨大的計算量致使SCG方法在實際中難以執(zhí)行.為了克服SCG方法計算量大的缺陷,本文提出了一種改進的SCG方法,記為ISCG(improved spectral coarse graining)算法,將計算復(fù)雜度從O(N3)降到O(N2),同時還改善了粗粒化效果,所得粗粒化網(wǎng)絡(luò)能夠更好地保持初始網(wǎng)絡(luò)的同步能力.

2 網(wǎng)絡(luò)同步能力的刻畫

考慮N個節(jié)點的復(fù)雜網(wǎng)絡(luò),其動力學(xué)方程為

其中xi∈Rm表示第i個節(jié)點的m維狀態(tài)變量;是第i個節(jié)點的動態(tài)方程;δ＞0為耦合強度;H(·):Rm→Rm是節(jié)點內(nèi)部耦合函數(shù); Laplacian矩陣L=(Lij)N×N∈RN×N為外部耦合矩陣,刻畫了網(wǎng)絡(luò)的耦合拓撲結(jié)構(gòu).若網(wǎng)絡(luò)節(jié)點j和i(i=j)相連,則Lij=1,否則Lij=0;Laplacian矩陣L的對角線元素滿足,即矩陣L滿足耗散耦合條件:.當(dāng)網(wǎng)絡(luò)是無向無權(quán)的連通網(wǎng)絡(luò)時,對應(yīng)的矩陣L是對稱不可約的正半定矩陣,具有非負特征值且滿足0=λ1＜ λ2≤ ···≤ λN.網(wǎng)絡(luò)(1)同步狀態(tài)x1(t)=x2(t)=···=xN(t)=s(t)的同步流形s(t)滿足=F(s(t)),它可以是孤立節(jié)點的平衡點、周期軌道或混沌軌道.將方程(1)線性化,令ξi為第i個節(jié)點狀態(tài)的變分,得到變分方程

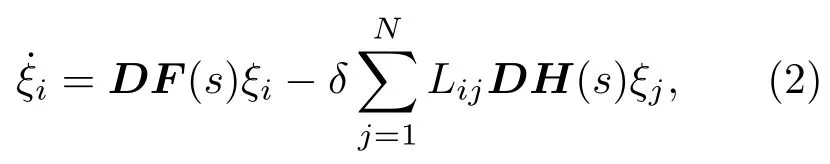
其中D F(s)和D H(s)分別是F(s)和H(s)關(guān)于s(t)的Jacobi矩陣.將方程(2)對角化可得到

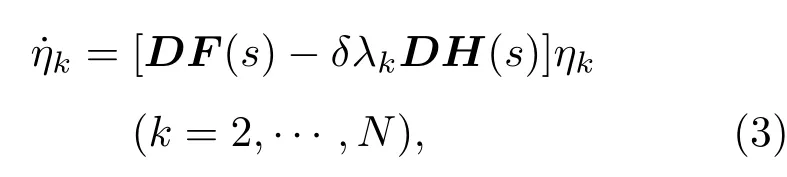
ηk是矩陣L關(guān)于特征值λk的特征模式.將方程(3)一般化,得到主穩(wěn)定方程:

該方程的最大Lyapunov指數(shù)Lmax是實變量α的函數(shù),稱之為網(wǎng)絡(luò)(1)的主穩(wěn)定函數(shù),記為Lmax(α).網(wǎng)絡(luò)(1)的同步化區(qū)域是指使Lmax(α)＜ 0的實數(shù)α的取值范圍,記為SR,它是由孤立節(jié)點動力學(xué)函數(shù)F(xi(t))和內(nèi)連函數(shù)確定的,只要網(wǎng)絡(luò)的耦合強度δ與耦合矩陣L的特征值之積全部落入同步區(qū)域即δλk∈SR(k=2,3,···,N),網(wǎng)絡(luò)(1)就能達到完全同步[22].網(wǎng)絡(luò)的同步區(qū)域主要分為以下4種類型:1)有界區(qū)域(α1,α2); 2)無界區(qū)域(α1,+∞);3)若干個有界區(qū)域的并集∪(α1i,α2i);4)空集.一般地,3)和4)的情形下網(wǎng)絡(luò)很難或完全無法達到同步,幸運的是大多數(shù)網(wǎng)絡(luò)都是1)和2)兩種情形,此時只有當(dāng)L的特征值滿足λN/λ2＜ α2/α1或者λ2＞ α1/δ時網(wǎng)絡(luò)才能達到同步穩(wěn)定狀態(tài)(其中λ2和λN分別為Lap lacian矩陣的最小非零特征值和最大特征值).這意味著當(dāng)λN/λ2越小或者λ2越大時網(wǎng)絡(luò)更容易達到同步,因此在同步研究中,常常用特征值比λN/λ2和最小非零特征值λ2兩個指標(biāo)來刻畫網(wǎng)絡(luò)的同步能力[23].

3 基于網(wǎng)絡(luò)同步的SCG方法

3.1 SCG方法

由于網(wǎng)絡(luò)的同步能力可用λ2或λN/λ2來刻畫,因此要使粗粒化后的網(wǎng)絡(luò)仍保持原始網(wǎng)絡(luò)的同步能力,就應(yīng)使粗粒化前后網(wǎng)絡(luò)的λ2或λN/λ2盡可能接近或不變.2008年,Gfeller和Rios[20,21]提出的SCG方法就是依此設(shè)計的,在縮減網(wǎng)絡(luò)規(guī)模的同時,盡可能地保持網(wǎng)絡(luò)的同步能力.該方法主要解決了兩個關(guān)鍵問題:一是如何合并節(jié)點和更新邊;二是確定哪些節(jié)點可以被合并.

首先,對于如何合并節(jié)點和更新邊,SCG方法將初始網(wǎng)絡(luò)的N個節(jié)點標(biāo)記為i=1,2,···,N,粗粒化后網(wǎng)絡(luò)節(jié)點標(biāo)記為C=1,2,···,?N,?N為粗粒化后的網(wǎng)絡(luò)規(guī)模,C也表示初始網(wǎng)絡(luò)中的 ?N個團,每個團的節(jié)點將被合并為粗粒化網(wǎng)絡(luò)中的一個節(jié)點.粗粒化后網(wǎng)絡(luò)的邊(對應(yīng)新的Lap lacian矩陣可通過下面的矩陣乘積進行更新:

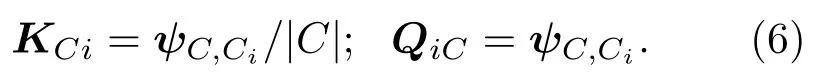
這里,|C|是團C中包含節(jié)點的個數(shù);Ci是節(jié)點i所在團C的標(biāo)號,ψ是常用的K ronecker函數(shù).

其次,對于哪些節(jié)點被合并,分別考慮λ2和λN/λ2兩個指標(biāo).若考慮指標(biāo)λ2(網(wǎng)絡(luò)(1)的Lap lacian矩陣L的最小非零特征值),記λ2對應(yīng)的特征向量為p2,將p2中相同或相近的分量對應(yīng)的節(jié)點進行合并,此時?L的最小非零特征值與λ2相同或相近. 理論上,特征向量p2的兩個分量和相同或相近,可表示為,其中和分別為p2的N個分量中的最大值和最小值.實際計算時,把區(qū)間劃分為I個等分區(qū)間,對落入同一等分區(qū)間的p2分量對應(yīng)的節(jié)點進行合并.一般地,I越小對應(yīng)的 ?N越小,因此可通過控制I值的大小來大致控制粗粒化網(wǎng)絡(luò)的規(guī)模.相同或相似節(jié)點的合并過程及λ2的保持情況如圖1所示.

同理,當(dāng)考慮指標(biāo)λN/λ2(網(wǎng)絡(luò)(1)的Laplacian矩陣L中最大與最小非零特征值之比)時,合并節(jié)點需同時滿足條件和.實際計算時分別把區(qū)間,劃分為I個等分區(qū)間(其中pN為最大特征值λN對應(yīng)的特征向量),找出p2和pN中同時落入等分區(qū)間內(nèi)的分量,將其對應(yīng)的節(jié)點進行合并.此時?L的特征值比與λN/λ2相同或相近,即能保持粗粒化網(wǎng)絡(luò)的同步能力.

圖1顯示,把結(jié)構(gòu)相同或相似的節(jié)點進行合并,網(wǎng)絡(luò)的最小非零特征值λ2變化不大,即網(wǎng)絡(luò)的同步能力能夠很好地被保持.

圖1 (網(wǎng)刊彩色)合并節(jié)點過程[21]Fig.1.(color on line)Processing ofm erging nodes[21].

3.2 SCG方法的局限

我們通過大量仿真實驗發(fā)現(xiàn),很多網(wǎng)絡(luò)的特征向量分量分布極不均勻,大多數(shù)分量分布相對集中、間距較小,極少數(shù)分量分布特別分散且間距很大.以節(jié)點N=100的NW小世界網(wǎng)絡(luò)為例,根據(jù)特征值λ2對應(yīng)的特征向量p2,將區(qū)間劃分為I=15的等分區(qū)間,p2的分量落入等分區(qū)間內(nèi)的分布情況如圖2所示,圖2中菱形對應(yīng)p2的所有分量,16條豎線將區(qū)間劃分為15個等分區(qū)間.從圖2可看出,p2的分量分布極不均勻.因此等區(qū)間劃分節(jié)點時可能造成有些距離特別近的兩個分量(對應(yīng)極相似的節(jié)點,如圖2中藍色菱形對應(yīng)分量和錳紫色菱形對應(yīng)分量)被分割到兩個相鄰區(qū)間中,而與間距更大的分量(對應(yīng)不太相似的節(jié)點)劃分到同一區(qū)間而合并相應(yīng)節(jié)點,這會影響粗粒化效果.另一方面,計算中需要將每一個p2分量與等分區(qū)間所有的端點值進行比較,依此判斷落在哪個等分區(qū)間內(nèi),這會造成較大的計算量,特別是對規(guī)模巨大的網(wǎng)絡(luò)更為明顯,其計算復(fù)雜度為O(N3)[16].例如,當(dāng)網(wǎng)絡(luò)節(jié)點N=1000時,SCG方法的計算量達到10億次.此外,由于p2的分量分布極不均勻,一些等分區(qū)間內(nèi)沒有分量落入,導(dǎo)致合并后的網(wǎng)絡(luò)規(guī)模隨I變化不大.例如,節(jié)點N=1000的NW小世界網(wǎng)絡(luò),當(dāng)劃分等區(qū)間數(shù)I為102,103,104,105,106時,分別為14,69, 381,871,991,因此I值對網(wǎng)絡(luò)規(guī)模的控制效果并不理想,也在一定程度上會影響粗粒化效果.綜上所述,SCG化方法存在兩方面的缺陷.一是計算量過大,對于大規(guī)模網(wǎng)絡(luò)實際計算難以實現(xiàn);二是對某些網(wǎng)絡(luò)粗粒化效果并不十分理想.

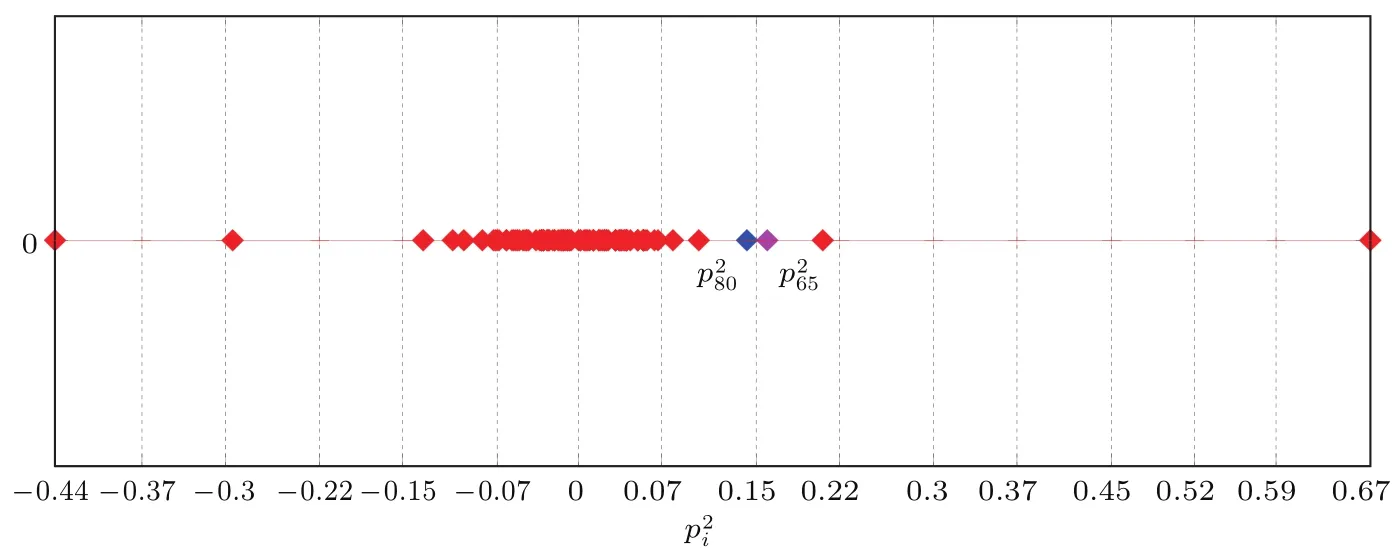
圖2 (網(wǎng)刊彩色)特征向量p2的分量分布情況Fig.2.(color on line)Distribution of com ponentsof eigenvector p2.

4 改進的SCG算法

本節(jié)我們在原方法的基礎(chǔ)上提出一種改進的SCG算法,不僅降低了計算復(fù)雜度,還改善了粗粒化效果,使粗粒化后的網(wǎng)絡(luò)更好地保持初始網(wǎng)絡(luò)的同步能力.

與SCG方法采取等分區(qū)間確定合并節(jié)點的做法不同,ISCG算法依特征向量分量的分布情況采取分裂聚類方法來確定合并節(jié)點.具體做法是:先將特征向量分量由小到大排序,計算兩兩相鄰分量間的距離,根據(jù)相鄰分量之間的間距大小將分量分裂成若干個聚類,然后將每個聚類中對應(yīng)的節(jié)點合并為一個節(jié)點.選擇間距的大小將決定同一聚類中節(jié)點的相似程度和粗粒化網(wǎng)絡(luò)的規(guī)模.例如,選擇較大的前?1個間距將所有分量分裂成個聚類,這個聚類對應(yīng)節(jié)點合并為個節(jié)點,從而可以精確控制網(wǎng)絡(luò)的規(guī)模,越大,相鄰分量的間距越小,合并節(jié)點的相似度越高,粗粒化效果越好.

下面我們以保持λ2為例進一步說明ISCG算法的步驟. 首先假設(shè)λ2的特征向量p2的分量由小到大排序為相鄰分量之間的間距為i=1,···,N?1),假設(shè)選擇最大的前3個間距,分別記為這3個間距將分裂成4個聚類,分別為,其中間距分裂區(qū)間時對應(yīng)的左右端點分別為和和和,再將這4個聚類中對應(yīng)的節(jié)點進行合并,即得到 ?N=4的粗粒化網(wǎng)絡(luò).由此可見,ISCG算法可以根據(jù)需要,選擇一定的間距將原始網(wǎng)絡(luò)N個節(jié)點合并到任何指定規(guī)模 ?N的粗粒化網(wǎng)絡(luò),并且合理區(qū)分不同節(jié)點間的相似程度,從而能確保被合并節(jié)點之間的相似程度高于不同聚類之間節(jié)點的相似程度,因此粗粒化效果較SCG方法更好.在計算量方面,由于ISCG算法只需計算分量之間的間距,而不需判斷比較每一個特征向量分量落入等區(qū)間的情況,只要確定了粗粒化網(wǎng)絡(luò)模型,便可一次完成所有節(jié)點的合并,因此大幅減少了計算量,其計算復(fù)雜度為O(N2).此外,ISCG算法能精確控制粗粒化網(wǎng)絡(luò)規(guī)模,這點優(yōu)于SCG算法對粗粒化網(wǎng)絡(luò)規(guī)模的控制.

類似地,對于保持特征值比λN/λ2的情況,可根據(jù)λ2和λN的特征向量p2和pN的分量之間的間距將各分量分裂成不同的聚類,將同時分裂在同一聚類中對應(yīng)節(jié)點合并為一個節(jié)點,計算過程與上述保持λ2的情形類似,這里不再贅述.

5 數(shù)值仿真

本節(jié)將分別對連續(xù)時間動態(tài)網(wǎng)絡(luò)和耦合相振子網(wǎng)絡(luò)模型進行數(shù)值仿真,分別應(yīng)用ISCG算法和SCG方法對網(wǎng)絡(luò)進行粗粒化,比較兩種不同粗粒化算法對幾種典型網(wǎng)絡(luò)同步能力的保持效果.

5.1 連續(xù)時間動態(tài)網(wǎng)絡(luò)的同步效果

下面對連續(xù)時間動態(tài)網(wǎng)絡(luò)模型(1)進行數(shù)值仿真.分別選取四種典型的復(fù)雜網(wǎng)絡(luò),即NW小世界網(wǎng)絡(luò)、ER隨機網(wǎng)絡(luò)、BA無標(biāo)度網(wǎng)絡(luò)和一類復(fù)雜聚類網(wǎng)絡(luò)[15],分別應(yīng)用ISCG和SCG算法粗粒化網(wǎng)絡(luò),觀察并比較粗粒化效果.原始網(wǎng)絡(luò)規(guī)模均為N=1000.

圖3和圖4展示了分別采用ISCG和SCG兩種算法對四種典型網(wǎng)絡(luò)進行粗粒化的結(jié)果和網(wǎng)絡(luò)同步能力的保持情況.無論對哪種網(wǎng)絡(luò),采取ISCG算法獲得的粗粒化網(wǎng)絡(luò)與原始網(wǎng)絡(luò)的λ2和λN/λ2的近似程度都明顯優(yōu)于SCG方法獲得的粗粒化網(wǎng)絡(luò),說明ISCG算法的粗粒化效果和同步能力保持情況優(yōu)于SCG方法.從運算時間上看,在實驗中獲得相同規(guī)模的粗粒化網(wǎng)絡(luò),ISCG算法比SCG方法所用的時間大大減少.以上述N=1000的NW小世界網(wǎng)絡(luò)為例,在保持λ2的情形,獲得 ?N=600的粗粒化網(wǎng)絡(luò),采用ISCG算法和SCG方法在MATLAB軟件試驗中的運行時間分別是2.94 s和18.4 s.實際上,由于后者需要經(jīng)過多次反復(fù)實驗才能獲得規(guī)模 ?N=600的粗粒化網(wǎng)絡(luò),故實際獲得結(jié)果時間遠不止18.4 s,而ISCG算法可以精確控制粗粒化網(wǎng)絡(luò)規(guī)模,一次完成實驗,故運行時間只需要2.94 s,可見ISCG算法的運算速度大幅提高.此外, ISCG算法可以精確獲得任意規(guī)模的粗粒化網(wǎng)絡(luò),從而能夠更精細地展示網(wǎng)絡(luò)的粗粒化演變過程,而SCG方法卻做不到這點.當(dāng)然,粗粒化網(wǎng)絡(luò)規(guī)模越小,合并的節(jié)點就越多,對原始網(wǎng)絡(luò)同步能力的保持效果越差,但對于同等規(guī)模的粗粒化網(wǎng)絡(luò),顯然ISCG算法的同步能力的保持效果更好.

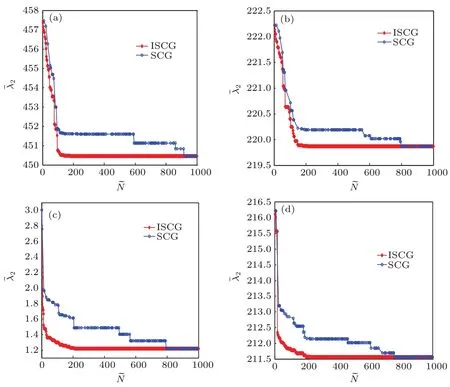
圖3 (網(wǎng)刊彩色)分別采用ISCG和SCG算法獲得粗粒化網(wǎng)絡(luò)對λ2的保持情況 (a)NW小世界網(wǎng)絡(luò);(b)ER隨機網(wǎng)絡(luò);(c)BA無標(biāo)度網(wǎng)絡(luò);(d)聚類網(wǎng)絡(luò)Fig.3.(color on line)Them aintaining ofλ2obtained by using ISCG and SCG algorithm s in coarse graining network:(a)NW network;(b)ER network;(c)BA network;(d)clustered network.

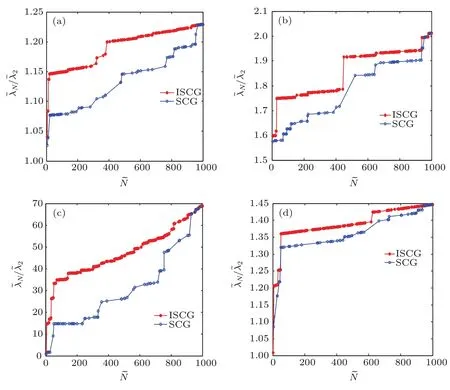
圖4 (網(wǎng)刊彩色)分別采用ISCG和SCG算法獲得粗粒化網(wǎng)絡(luò)對λN/λ2的保持情況 (a)NW 小世界網(wǎng)絡(luò); (b)ER隨機網(wǎng)絡(luò);(c)BA無標(biāo)度網(wǎng)絡(luò);(d)聚類網(wǎng)絡(luò)Fig.4.(color on line)The m aintaining ofλN/λ2obtained by using ISCG and SCG algorithm s in coarse graining network:(a)NW network;(b)ER network;(c)BA network;(d)clustered network.

5.2 耦合K u ram oto相振子網(wǎng)絡(luò)的同步效果

下面對耦合Kuramoto網(wǎng)絡(luò)[24,25]模型進行數(shù)值仿真,進一步比較ISCG和SCG算法對保持相振子同步的效果.耦合Kuramoto網(wǎng)絡(luò)模型方程為

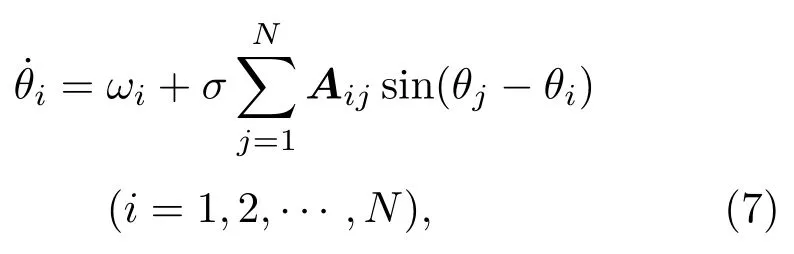
其中,ωi表示第i個振子的固有頻率,σ表示全局振子耦合強度,Aij為鄰接矩陣,θi表示第i個振子的相位,N表示振子的個數(shù).全局振子的相同步程度可用序參量r(t)刻畫:

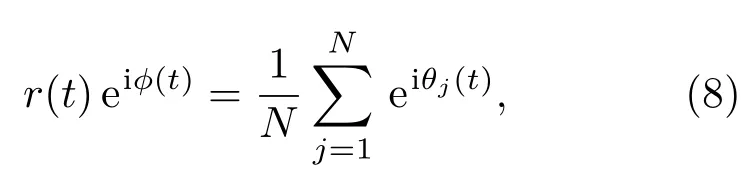
其中序參量r(t)(∈[0,1])為0時表示全局振子以各自的固有頻率運動,即完全不同步狀態(tài),為1時表示全局振子以相同頻率運動,即達到完全同步狀態(tài);?(t)表示全局振子的平均相位.因此可通過序參量r(t)來研究粗粒化網(wǎng)絡(luò)的同步保持情況.

以上文N=1000的NW小世界網(wǎng)絡(luò)、ER隨機網(wǎng)絡(luò)、BA無標(biāo)度網(wǎng)絡(luò)、聚類網(wǎng)絡(luò)為例,采用ISCG和SCG算法粗粒化網(wǎng)絡(luò),得到網(wǎng)絡(luò)規(guī)模 ?N均為200的ISCG網(wǎng)絡(luò)和SCG網(wǎng)絡(luò),ωi在(?0.5,0.5)中隨機選擇,初始相位θi在(?π,π)中隨機選擇,σ分別為0.2,0.2,1.5,0.5.其序參量r(t)保持情況如圖5所示.

圖5展示了分別采用ISCG和SCG兩種算法對振子相同步的保持情況,可見ISCG獲得網(wǎng)絡(luò)的序參量r(t)收斂性與原始網(wǎng)絡(luò)基本一致,且ISCG算法獲得的粗粒化網(wǎng)絡(luò)同步能力保持情況優(yōu)于SCG方法.

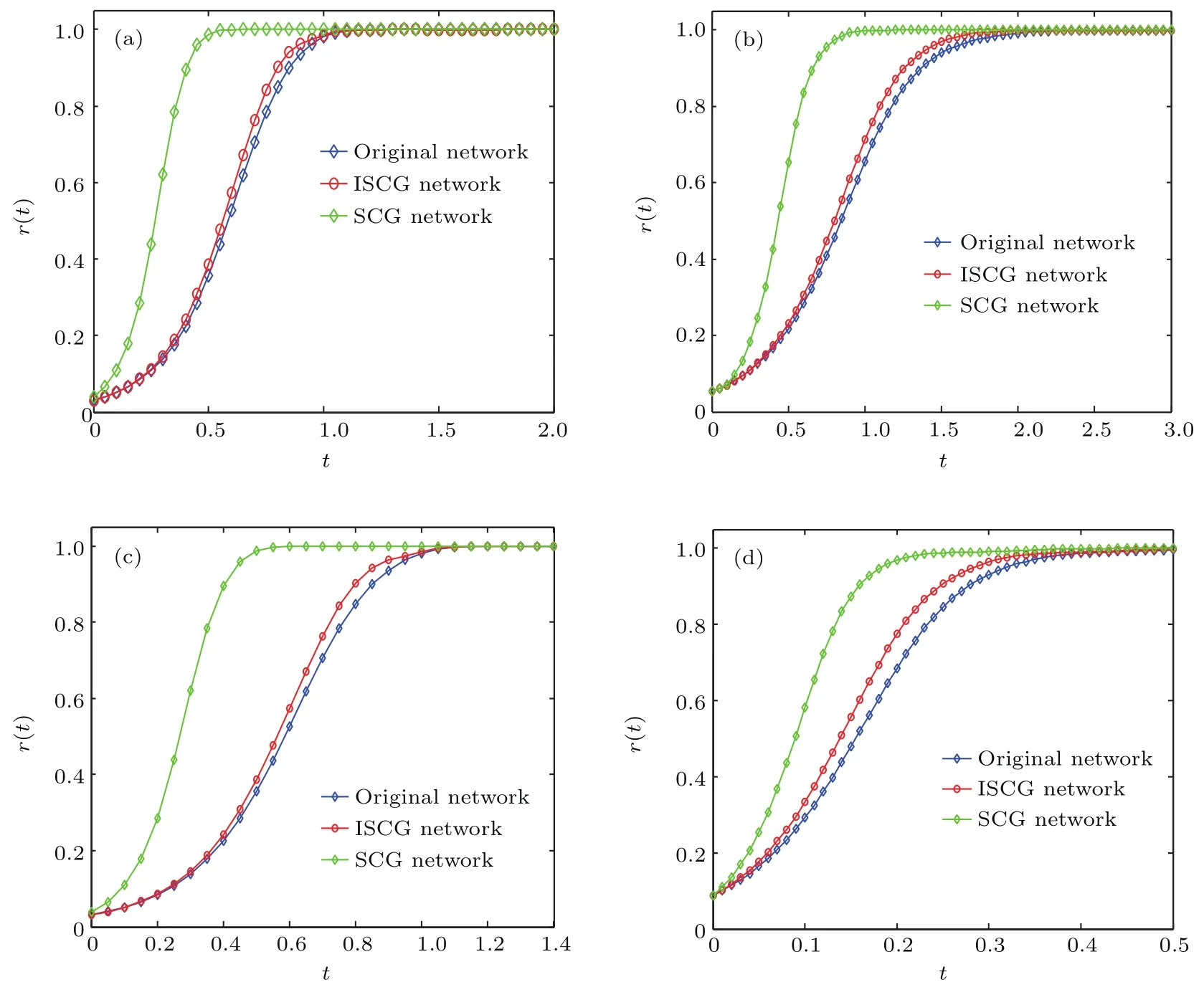
圖5 (網(wǎng)刊彩色)分別采用ISCG和SCG算法保持序參量r(t)的情況 (a)NW小世界網(wǎng)絡(luò);(b)ER隨機網(wǎng)絡(luò); (c)BA無標(biāo)度網(wǎng)絡(luò);(d)聚類網(wǎng)絡(luò)Fig.5.(color on line)The m aintaining of the order param eter r(t)obtained by using ISCG and SCG algorithm s in coarse graining network:(a)NW network;(b)ER network;(c)BA network;(d)clustered network.

6 結(jié) 論

復(fù)雜動態(tài)網(wǎng)絡(luò)的耦合拓撲結(jié)構(gòu)直接影響網(wǎng)絡(luò)的動力學(xué)性質(zhì).一般來說,兩個節(jié)點的外部連接相同或相近,意味著它們接收外部的信息和作用也相同或相近,因而具有相近的動力學(xué)性質(zhì),SCG方法的基本思想正是基于這一點,把網(wǎng)絡(luò)中外部鏈接相同或相近似的節(jié)點進行合并,從而把大規(guī)模網(wǎng)絡(luò)縮減為中尺度網(wǎng)絡(luò),這是研究大規(guī)模網(wǎng)絡(luò)的重要途徑之一.本文提出的ISCG算法,以特征向量分量之間的間距大小來劃分相似節(jié)點,從而自適應(yīng)地對聚類節(jié)點進行分組,能夠確保網(wǎng)絡(luò)中越相近的節(jié)點越被優(yōu)先合并,避免了SCG方法對節(jié)點進行硬性分組而導(dǎo)致某些情況下相似節(jié)點被拆分而與不相近節(jié)點合并的缺陷.仿真實驗也驗證了ISCG算法既能很好地改善粗粒化效果,又大幅降低了運算的時間復(fù)雜度.

從算法分析和仿真結(jié)果看,在粗粒化過程中應(yīng)該存在一個最優(yōu)的聚類個數(shù),即存在一個既能很好地保持原始網(wǎng)絡(luò)同步能力又能最大程度地縮減原始網(wǎng)絡(luò)規(guī)模的聚類個數(shù),例如,用λ2來刻畫網(wǎng)絡(luò)的同步能力,可以滿足(ε比較小,可設(shè)定)的對應(yīng)的最小 ?N即為最優(yōu)聚類個數(shù).以上文中所列舉的四種典型即NW小世界網(wǎng)絡(luò)、ER隨機網(wǎng)絡(luò)、BA無標(biāo)度網(wǎng)絡(luò)和聚類網(wǎng)絡(luò)為例,可求得最優(yōu)聚類個數(shù) ?N分別為915,805,795,768.然而,對于最優(yōu)的聚類個數(shù)問題,還有更多的未知需要我們?nèi)ヌ剿?例如衡量最優(yōu)粗粒化聚類個數(shù)的指標(biāo)函數(shù)如何確定?各種不同結(jié)構(gòu)的網(wǎng)絡(luò)的最優(yōu)指標(biāo)有何差異?且有待我們進行更深入的探索研究,也是我們今后的努力方向.

本文提出的ISCG算法具有誤差更小、效果更優(yōu)、運算量大幅降低等諸多優(yōu)點,能極大地改善原粗粒化效果,提高了網(wǎng)絡(luò)同步能力的保持狀況,同時為實現(xiàn)大規(guī)模網(wǎng)絡(luò)的同步研究提供了一種更簡單、高效和可操作的有效方法.

[1]Pecora L M,Carroll T L 1998 Phys.Rev.Lett.80 2109

[2]Jost J,Joy M P 2001 Phys.Rev.E 65 016201

[3]W ang X F,Chen G R 2002 IEEE Trans.Circuits-I 49 54

[4]Barahona M,Pecora L M 2002 Phys.Rev.Lett.89 054101

[5]W ang X F,Chen G R 2002 In t.J.Bifurcat.Chaos 12 187

[6]M otter A E,Zhou C S,Kurths J 2005 Phys.Rev.E 71 016116

[7]N ishikawa T,M otter A E 2006 Physica D 224 77

[8]Zhou J,Lu JA,Lu JH 2006 IEEE Trans.Au to.Con trol 51 652

[9]A renas A,Díaz-Guilera A,Kurths J,M oreno Y,Zhou C S 2008 Phys.Rep.469 93

[10]Zhu T X,W u Y,X iao J H 2012 Acta Phys.Sin.61 040502(in Chinese)[朱廷祥,吳曄,肖井華2012物理學(xué)報61 040502]

[11]Xu M M,Lu JA,Zhou J 2016 Acta Phys.Sin.65 028902 (in Chinese)[徐明明,陸君安,周進 2016物理學(xué)報 65 028902]

[12]K urkcuoglu O,Jernigan R L,Doruker P 2004 Polym er 45 649

[13]M arrink S J,Vries A H D,M ark A E 2004 J.Phys. Chem.B 108 750

[14]Bornhold t S 2005 Science 310 449

[15]Chen J,Lu J A,Lu X F,W u X Q,Chen G R 2013 Comm un.Non linear Sci.18 3036

[16]Zeng A,LüL Y 2011 Phys.Rev.E 83 056123

[17]Saunders M G,Voth G A 2013 Annu.Rev.Biophys.42 73

[18]K im B J 2004 Phys.Rev.Lett.93 168701

[19]Chen H S,Hou Z H,Xin HW,Yan Y J 2010 Phys.Rev. E 82 011107

[20]G feller D,Rios P D L 2007 Phys.Rev.Lett.99 038701

[21]G feller D,Rios P D L 2008 Phys.Rev.Lett.100 174104

[22]Chen G R,W ang X F,Li X,LüJ H 2009 Som e Recen t Advances in Com plex Networks Synchronization(Heidelberg:Sp ringer)pp3–16

[23]Lu JA,Liu H,Chen J 2016 Synchronization in Com plex Dynam ical Networks(Beijing:Higher Education Press) pp120–125(in Chinese)[陸君安,劉慧,陳娟2016復(fù)雜動態(tài)網(wǎng)絡(luò)的同步(北京:高等教育出版社)第120—125頁]

[24]Kuram oto Y 1975 Lect.Notes Phys.39 420

[25]Aceb rón J A,Bonilla L L,Pérez V icente C J,Ritort F, Sp igler R 2005 Rev.M od.Phys.77 137

PACS:05.45.–a,05.45.X tDOI:10.7498/aps.66.060502

Im p roved algorithm of spectral coarse grain ing m ethod of com p lex netw ork?

Zhou Jian1)Jia Zhen1)?Li Ke-Zan2)

1)(College of Science,Guilin University of Technology,Guilin 541004,China)
2)(School ofM athem atics and Com puting Science,Guilin University of E lectronic Technology,Guilin 541004,China)
(Received 2 O ctober 2016;revised m anuscrip t received 21 Novem ber 2016)

Com p lex network as a key app roach to understandingmany com p lex system s,such as biological,chem ical,physical, technological and social system s,is ubiquitous in nature and society.Synchronization of large-scale com p lex networks is one of the m ost im portant issues in network science.In the last two decades,much attention has been paid to the synchronization of com p lex dynam ic networks,especially themeso-scale networks.However,many real networks consist of even hundreds ofm illions of nodes.Analyzing the synchronization of such large-scale coup led com p lex dynam ic networks often generate a large number of coup led diff erentialequations,which m ay m akem any synchronization algorithm s inapp licable formeso-scale networks due to the com p lexities of simu lation experiments.Coarse grainingmethod canmap the large-scale networks into m eso-scale networks while preserving som e of topological p roperties or dynam ic characteristics of the original network.Especially,the spectral coarse-graining scheme,as a typical coarse grainingmethod,is proposed to reduce the network size while preserving the synchronization capacity of the initial network.Nevertheless, p lenty of studies dem onstrate that the com ponents of eigenvectors for the eigenvalue of the coup ling m atrix,which can depict the ability to synchronizing networks,distribute uneven ly.Most of the com ponents distribute concentrically and the intervals are sm all,while som e other com ponents distribute dispersed ly and the intervals are large,which renders the app lications of original spectral coarse graining m ethod unsatisfactory.Inspired by the adap tive clustering,we p ropose an im proved spectral coarse graining algorithm,which clusters the same or the sim ilar nodes in the network according to the distance between the com ponents of eigenvectors for the eigenvalue of network coup ling m atrices,so that the nodesw ith the sam e or the sim ilar dynam ic properties can be eff ectively clustered together.Com pared w ith the original spectral coarse graining algorithm,thismethod can im p rove the accuracy of the result of clustering.M eanwhile,our m ethod can greatly reduce algorithm com p lexity,and obtain better spectral coarse graining resu lt.Finally,num erical simulation experim ents are im p lem ented in four typical com p lex networks:NW network,ER network,BA scale-free network and clustering network.The com parison of results demonstrate that ourmethod outperform s the original spectral coarse graining approach under various criteria,and im proves the eff ect of coarse graining and the ability to synchronize networks.

comp lex network,synchronization,spectral coarse graining,im proved algorithm

10.7498/aps.66.060502

?國家自然科學(xué)基金(批準(zhǔn)號:61563013,61663006)資助的課題.

?通信作者.E-m ail:jjjzzz0@163.com

*Pro ject supported by the National Natural Science Foundation of China(G rant Nos.61563013,61663006).

?Corresponding author.E-m ail:jjjzzz0@163.com