基于全矢融合與多維經驗模態分解的滾動軸承退化過程頻譜結構研究

馬艷麗 金 兵 張學欣 韓 捷

鄭州大學振動工程研究所，鄭州，450001

?

基于全矢融合與多維經驗模態分解的滾動軸承退化過程頻譜結構研究

馬艷麗 金 兵 張學欣 韓 捷

鄭州大學振動工程研究所，鄭州，450001

為了識別滾動軸承退化過程，提出一種多維經驗模態分解和全矢融合相結合的方法。首先對不同狀態的多通道信號同時進行多維經驗模態分解，得到一系列多元固有模態函數分量，然后利用互相關系數準則選取最敏感的一階固有模態函數分量進行全矢包絡分析來提取信號的特征。為了驗證該方法的有效性，分別對模擬信號和實際信號進行了分析。結果表明此方法在出現故障時，能夠很好地表征頻譜結構的變化；隨著故障嚴重程度的增加，頻譜結構變得復雜，且呈現出了規律性。

多維經驗模態分解；全矢融合；頻譜結構；軸承退化

0 引言

滾動軸承是重要的機械基礎件，廣泛用于各個領域[1]，因此對滾動軸承退化狀態進行監測與故障程度診斷具有重要意義。滾動軸承的振動信號一般呈現非線性、非平穩特征。經驗模態分解(EMD)在處理多通道信號時，把每一個序列作為一個獨立變量，單獨對每一個序列進行分解，往往會出現尺度排列不確定性問題和同階尺度頻率不一致問題[2]。REHMAN等[3]提出了多維經驗模態分解(multivariate empirical mode decomposition，MEMD)方法，對EMD算法進行了改進，使其能同時處理多通道信號，并保證各通道分解得到的固有模態函數(intrinsic mode function,IMF)分量數量一致且對應階頻率成分一致，從而便于多維數據的融合。MEMD方法應用在高速列車轉向架、齒輪的故障診斷中時都具有良好的效果[4-5]。文獻[6]把噪聲輔助MEMD和多尺度形態學相結合，提出了一種滾動軸承故障診斷方法，提高了軸承故障檢測精度，但也存在只能處理單通道信號，信息不完善的缺陷。

由于單通道分析存在信息利用不充分的問題，因此韓捷等[7]提出了基于同源信息融合的全矢譜技術，將各個諧波下的主振矢作為此頻率處的振動強度，解決了單通道振動信號特征提取不完整的問題。 文獻[8]將全矢融合技術應用于WTDS試驗臺的故障診斷，基于同源信息融合的全矢譜技術能正確地找到預設的故障位置，并準確地判斷出故障性質。文獻[9]把全矢融合技術和支持向量回歸模型相結合，提出了全矢支持向量回歸的頻譜預測新方法，該方法對汽輪機振動信號頻譜結構進行預測時具有較高的預測準確性。

1 MEMD和全矢融合算法

1.1 多維EMD算法

將多維信號沿著不同的方向投影得到多個方向向量，在各個方向上求取信號的包絡，通過計算包絡信號,可得多維信號的均值。定義q維信號x=(x1，x2，…，xq)，信號x的向量集D中的第l個方向向量Dl=(dl1，dl2，…，dlq)，MEMD的基本算法流程如下[9]：

(1)確定方向向量集D。

(2)在Dl上計算x的第l(l=1，2，…，L)個投影pl(t)，其中，L為方向向量個數，并確定pl(t)最大值所在的時刻tml。

(3)以[tml，x(tml)]為插值節點，獲取多維包絡線El(t)。

(4)計算包絡線均值M(t):

(1)

式中，El(t)為信號x在方向向量Dl上投影的包絡線值。

(5)計算剩余量R1(t):

R1(t)=x(t)-M(t)

(2)

式中，x(t)為原始信號,t=1，2，…，q。

如果R1(t)滿足多維IMF的迭代終止條件，則定義R1(t)為一階IMF分量，并以剩余量x(t)-R1(t)為對象重復步驟(2)～(5)，直至分離出下一階IMF分量。

1.2 互相關系數準則

相關關系是一種非確定性的關系，相關系數是研究變量之間線性相關程度的量。設有兩個序列x=(x1，x2，…，xn)和y=(y1，y2，…，yn) ，則它們的相關系數為

(3)

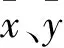
(1)分別計算nxnor和xnor，nynor和ynor之間的相關系數，并求這些相關系數的平均值，記為on。

(2)分別計算nxabn和xabn，nyabn和yabn之間的相關系數，并求這些相關系數的平均值，記為pn。

(3)計算nxnor和nynor分別與nxabn和nyabn的4個相關系數，并求這些相關系數的平均值，記為qn。

(4)計算敏感系數sn:

sn=(on+pn)/2-qn

(4)

式(4)中，on、pn表明分解得到的IMF分量與初始信號的相關程度，其值越大，IMF分量與初始信號越相似；qn表明同一階的IMF分量之間的相關性，其值越小，IMF分量變化越大。綜合來看，sn越大，這階的IMF分量越敏感，越能反映頻譜變化。

1.3 全矢融合算法

為保證信息的完整性，在旋轉機械的同一截面上安裝2個相互垂直的傳感器來提取振動特征。轉子的渦動是由各諧波頻率下的組合作用形成的，其渦動軌跡是一系列橢圓。設x、y方向上的數據序列分別為{xi}和{yi}，其構成的復序列為zi=xi+jyi，i=1，2，…，N/2-1；通過傅里葉變換有Zi=ZRi+ZIi，ZRi、ZIi分別為Zi的實部和虛部。

定義橢圓的長軸Rai為主振矢，橢圓的短半軸Rbi為副振矢，αi為主振矢和x軸的夾角,φi為該頻率下橢圓軌跡的初相位角。

一般用某個頻率上的主振矢代表這個頻率上的振動強度。根據傅里葉變換性質可得下式(推導過程參考文獻[10])：

(5)

1.4 MEMD和全矢融合算法流程

直接采集到的實際信號一般都會含有噪聲，對其處理時，首先用形態學濾波的方法消除部分噪聲；然后進行MEMD分解，利用互相關系數準則選取最敏感的IMF分量并對其進行包絡解調(包絡解調的目的是把與故障有關的信號從高頻調制信號中解調出來，從而避免與其他低頻相混淆)；最后進行全矢融合分析，提取主振矢。MEMD和全矢融合流程如圖1所示。

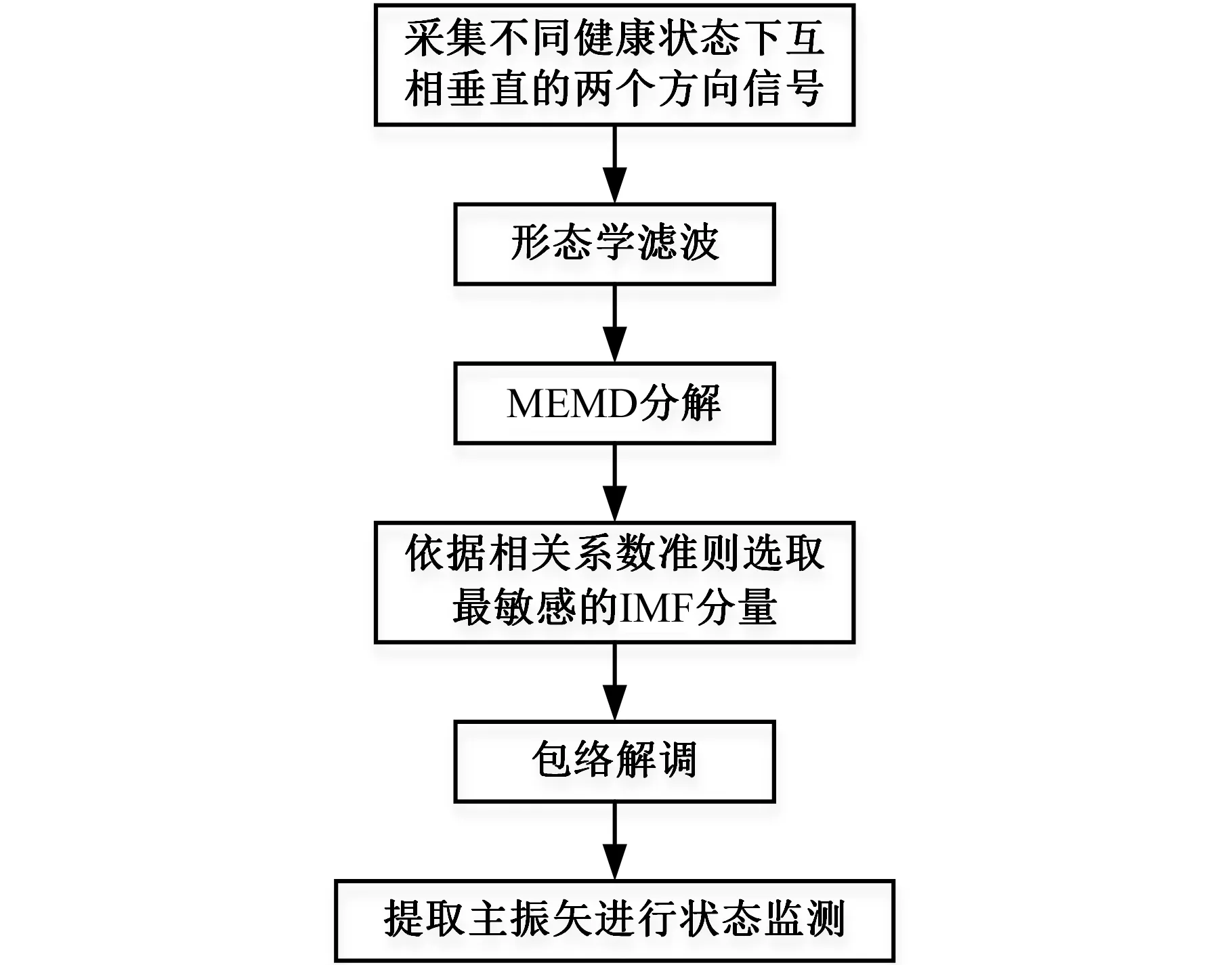
圖1 算法流程Fig.1 Flow of the algorithm

2 仿真分析

為了驗證MEMD與全矢融合相結合的方法在處理同源信號時的有效性，對模擬信號進行分析。對于滾動軸承信號來說，發生故障時的振動信號呈現調制現象。外圈固定結構的滾動軸承的振動信號為[11]

x(t)=αsin(2πfb)[1+βsin(2πfrt)]

(6)

式中，fb為滾動軸承的內圈通過頻率；fr為轉子的旋轉頻率。

基于此，構造如下的模擬加速度信號：

(7)

其中，xnor、ynor是正常運行情況下的兩個垂直方向的初始振動信號，xabn、yabn是異常情況下的兩個垂直方向的初始振動信號，采樣頻率fs=1024 Hz，采樣點數M=1024。利用MEMD對兩個狀態對應的雙通道仿真信號進行分解，分解結果如圖2所示，從圖2中可以看出，各通道分解得到的IMF分量數目全為4，并且按照頻率尺度對齊，這就為信號融合提供了條件[8]。xnor、ynor第二階IMF分量IMF2的振幅幾乎為零，xabn、yabn的IMF2則有明顯的振幅，可以比較完整地體現模擬信號由正常到異常的變化。通常故障信號主要包含在某些IMF分量里，需要從分解得到的前三階IMF分量中找到最能代表正常與故障狀態變化的一階分量，利用互相關系數準則，得到1～3階分量的互相關系數，分別為0.18、0.45、0.13，第二階IMF分量IMF2的互相關系數最大，因此取這一階進行全矢融合，結果如圖3所示。

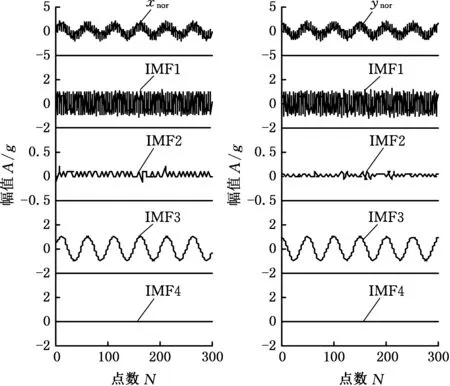
(a)x方向正常運行信號(b)y方向正常運行信號

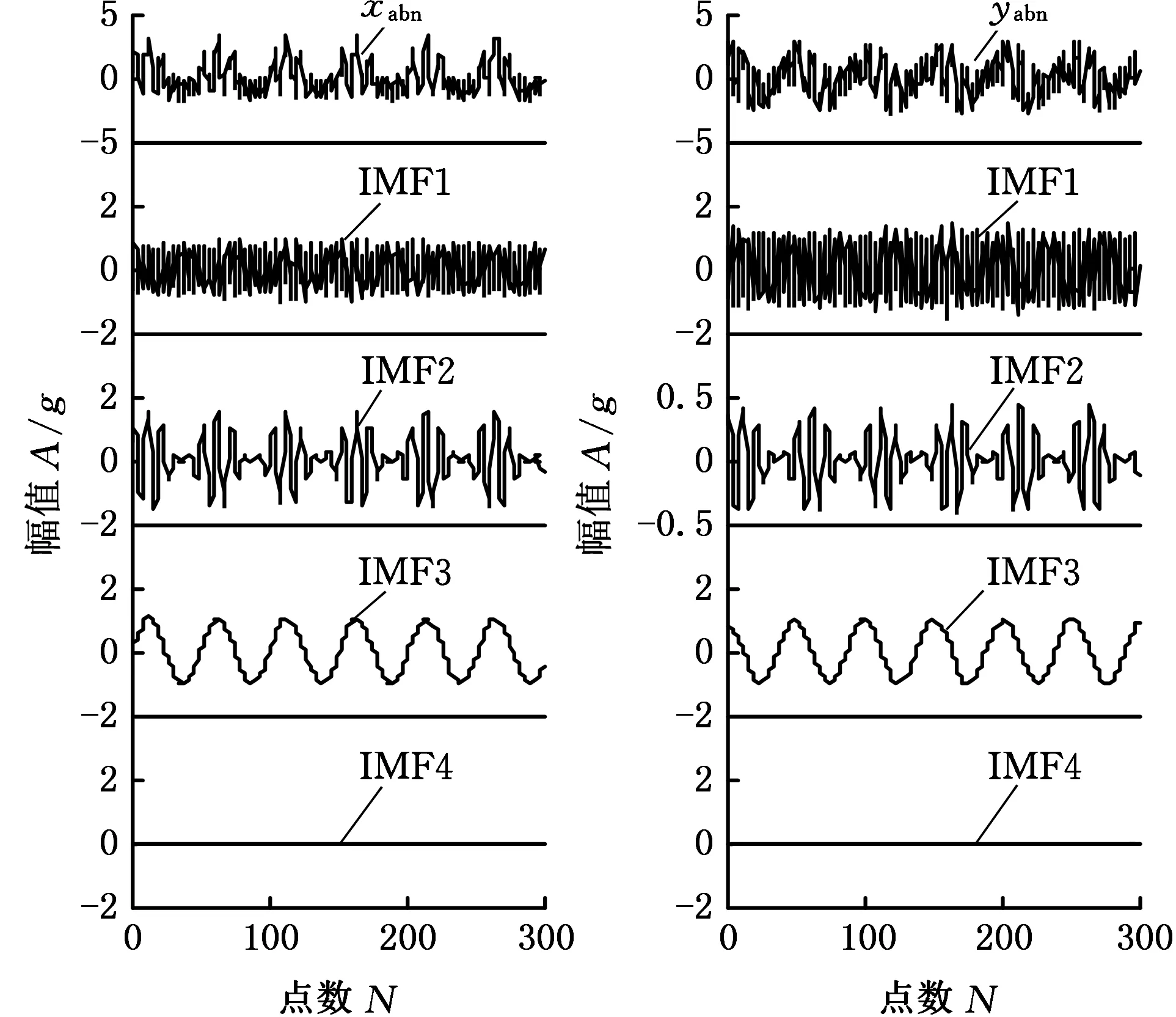
(c)x方向異常情況信號(d)y方向異常情況信號圖2 時間序列(模擬信號)Fig.2 Time series(analog signal)

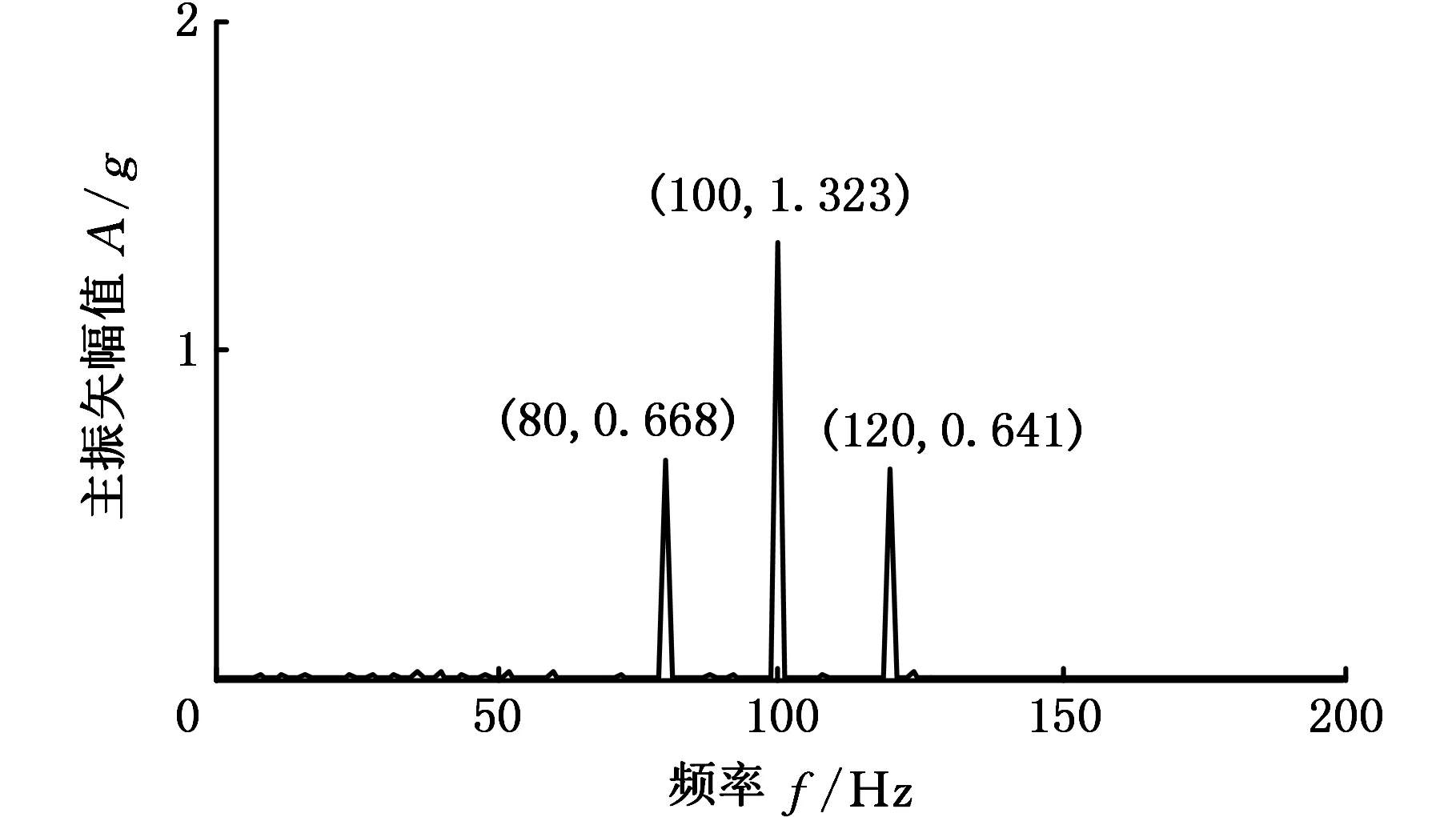
圖3 第二階IMF分量全矢融合圖Fig.3 Full vector fusionspectrum of the second IMF component

由于正常情況下的IMF2的振幅幾乎為零，故只把異常情況下的IMF2進行全矢融合，從圖3中可以看出，100 Hz處振動強烈，且出現了調制現象。異常情況信號xabn、yabn經過全矢融合后，在100 Hz處的振幅是1.323g，調制頻率80 Hz、120 Hz處的振幅分別是0.668g和0.641g，這些幅值融合了xabn、yabn的第二階IMF分量的信息。正常情況到異常情況的變化主要體現在后者出現了調制現象，第二階分量剛好能夠代表信號由正常到異常的頻譜結構變化。一般而言，對來自同一截面的雙通道信號分別進行頻譜分析時，會存在相同頻率處的振幅不同的問題，也會存在這兩個信號包含頻率成分不同的問題，利用全矢融合可以綜合雙通道的振動信息，能更加全面地反映軸承的運行狀態。

3 實例分析

為了進一步驗證本文所述方法的有效性，采用由辛辛那提大學智能維護中心提供的滾動軸承數據信號進行分析。軸承實驗臺的主軸上安裝了4個軸承，交流電機通過帶傳動帶動主軸旋轉，每個軸承上安裝了方向垂直的2個加速度傳感器，軸承2、3上加有徑向載荷，如圖4所示。軸承為ZA-2115雙列滾子軸承。軸的轉速大約是2000 r/min(33 Hz)，采樣頻率為20 kHz，采樣長度為20 480點，每隔10 min采集一次。在此實驗的最后，軸承3出現了內圈故障。根據軸的轉速和軸承參數，可計算得出軸承3的內圈故障頻率為294 Hz，采集軸承3處于正常狀態、輕微故障、中度故障、嚴重故障的數據進行分析，首先進行形態學濾波以消除部分噪聲。然后用MEMD處理，信號分解為12階IMF分量。依據互相關系數準則，分別計算出每階IMF分量的互相關系數，如表3所示。

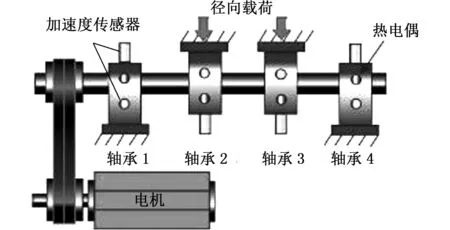
圖4 軸承實驗臺示意圖Fig.4 Sketch of bearing test rig

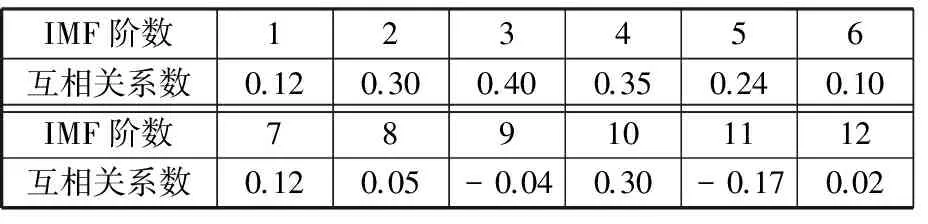
IMF階數123456互相關系數0．120．300．400．350．240．10IMF階數789101112互相關系數0．120．05-0．040．30-0．170．02

多通道信號經過MEMD分解后，可以保證各個狀態信號對應的IMF分量按照頻率尺度對齊，因此，可通過研究所有IMF分量中互相關系數最大的那一階分量來探究故障發展程度。第三階IMF分量的互相關系數最大，根據之前的分析可知，在一定程度上，第三階IMF分量可以代表滾動軸承出現的內圈故障的退化過程。4種狀況下的第三階IMF分量IMF3的時間序列如圖5所示，可直觀地看出，沖擊幅值隨故障程度的增加而增大，為了進一步觀察不同狀態下軸承振動的規律，采用了滾動軸承故障診斷常用的包絡分析方法。

(a)正常運行

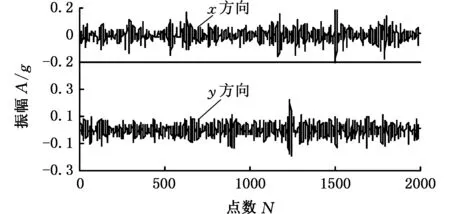
(b)輕微損傷

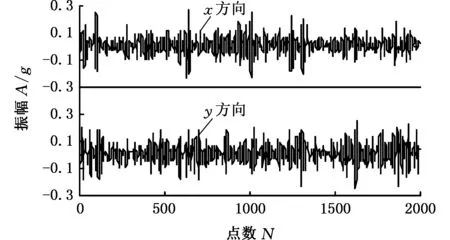
(c)中度損傷

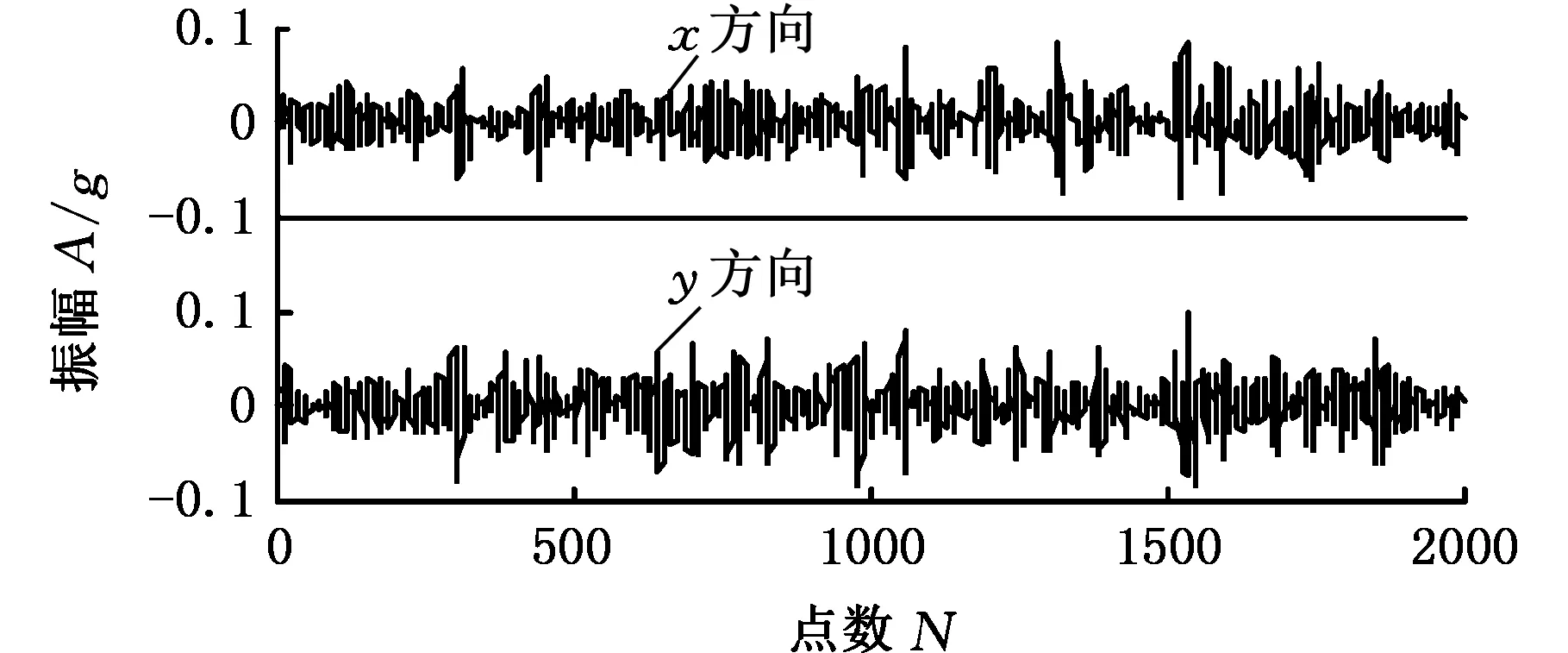
(d)嚴重損傷圖5 第三階IMF分量的時域圖(實際信號)Fig.5 Time-domain figure of the third IMF component

嚴重故障狀態下，對經MEMD分解的x、y方向信號的第三階IMF分量作包絡譜分析和全矢包絡譜分析，如圖6所示。圖6表明，不同故障程度下的兩個方向的信息雖然屬于同源信息，但是它們所包含的信息并不相同，圖6a顯示，x方向信號在66 Hz、132 Hz處振幅較小，在261 Hz、294 Hz處振幅較為明顯；圖6b顯示，y方向信號在66 Hz、132 Hz、261 Hz、294 Hz這四處頻率下的振動都較強烈，而全矢包絡譜則綜合了這2個方向的振動信息；圖6c表明，對x和y方向作全矢包絡分析后，66 Hz、132 Hz處的振幅較大，261 Hz和294 Hz處的振幅比x、y方向上振幅都大。故可以說明，全矢包絡譜綜合反映了x和y兩個方向上的振動信息。

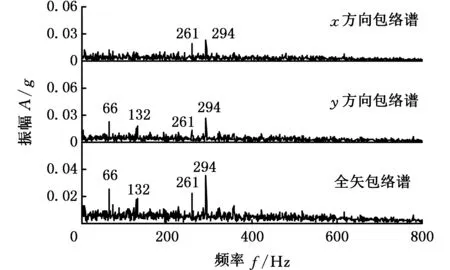
圖6 嚴重故障包絡譜Fig.6 Envelope spectrum of serious failure

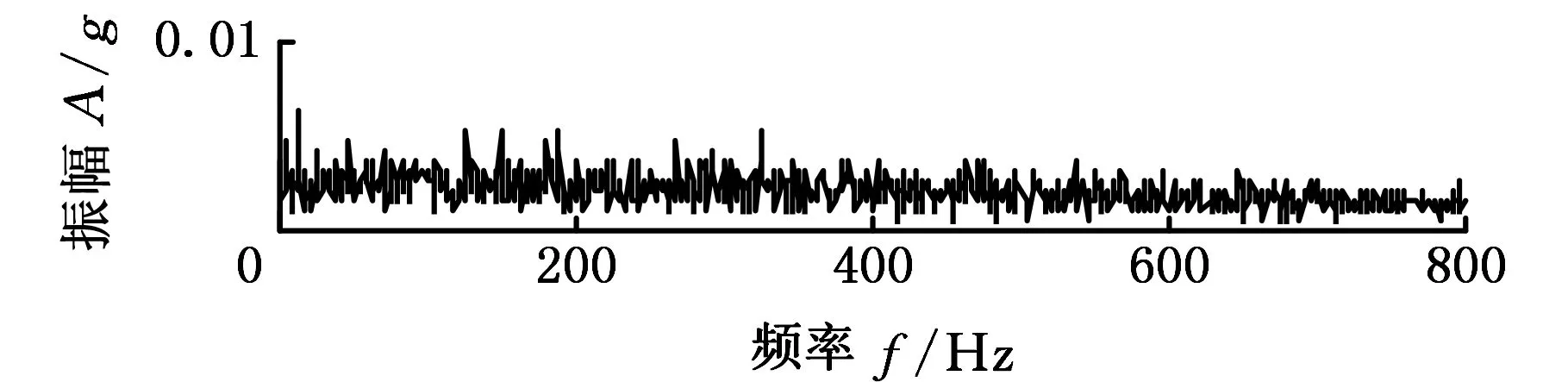
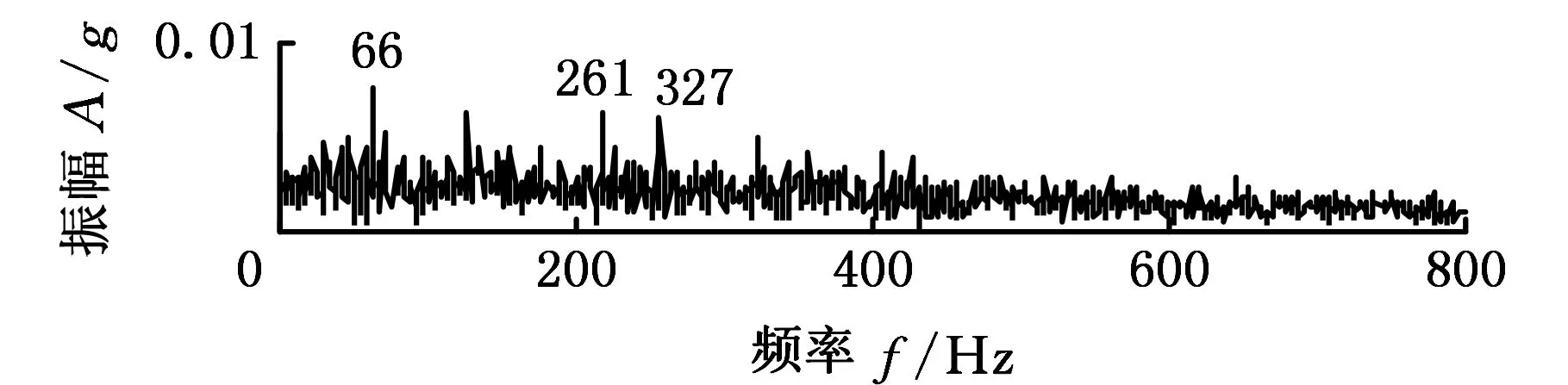
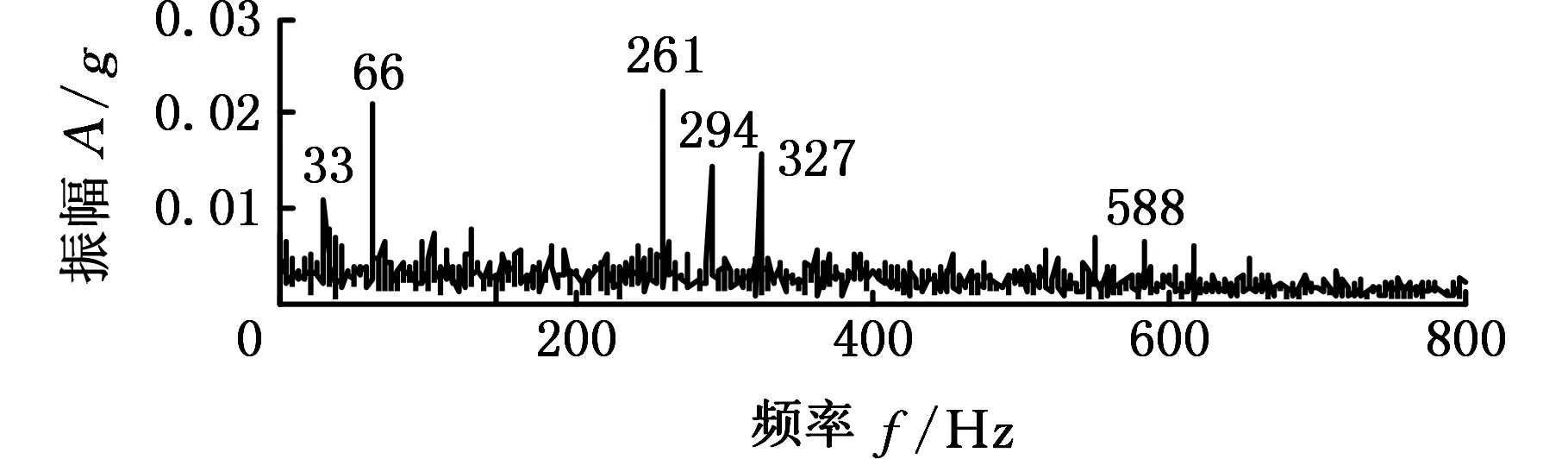
為了體現滾動軸承退化過程頻譜結構的變化，將不同狀態下對應的第三階IMF分量分別進行全矢包絡分析。由圖7a可以看出，軸承在正常運行情況下，整個頻帶上的頻譜分布很均勻；輕微故障狀態下的全矢包絡譜(圖7b)顯示，轉軸基頻的二倍頻66 Hz和軸承內圈故障特征頻率294 Hz處的幅值均有所突出，并且在內圈故障特征頻率附近出現了明顯的基頻的調制頻率(261 Hz、327 Hz)；隨著故障的進一步發展，基頻(33 Hz)、基頻的二倍頻、內圈故障特征頻率及內圈故障特征頻率的二倍頻(588 Hz)處振幅顯著增大，并且內圈故障特征頻率附近，有更加明顯的基頻的調制頻率，如圖7c所示；故障發展到嚴重程度時，整個頻率范圍內的振幅明顯增大，所有特征頻率依然明顯，尤其是基頻的二倍頻、內圈故障特征頻及調制頻率，如圖7d所示。對比這四種狀態可知，隨著故障程度的增大，整個頻帶上的振幅增大，基頻、故障特征頻率及調制頻率出現并且幅值增大。

為了對比說明該方法的有效性，對正常狀態到嚴重故障四種情況的初始信號直接進行全矢包絡譜分析，結果如圖8所示，可以看出，正常情況下的整體振幅較小；輕微故障時，整體振幅有所增大；中等故障時，特征頻率下的幅值變得明顯；嚴重故障時，振幅增大明顯。整體來看，全矢包絡方法的頻譜結構的變化不能有效表征軸承的退化過程。全矢MEMD包絡分析方法能夠有效融合多通道數據，并依據互相關系數，選取對軸承性能退化特征比較敏感的某一階IMF分量來表征滾動軸承的退化過程，其頻譜結構的變化能比較準確、全面地反映滾動軸承性能退化趨勢。

(a)正常運行

(b)輕微損傷

(c)中度損傷

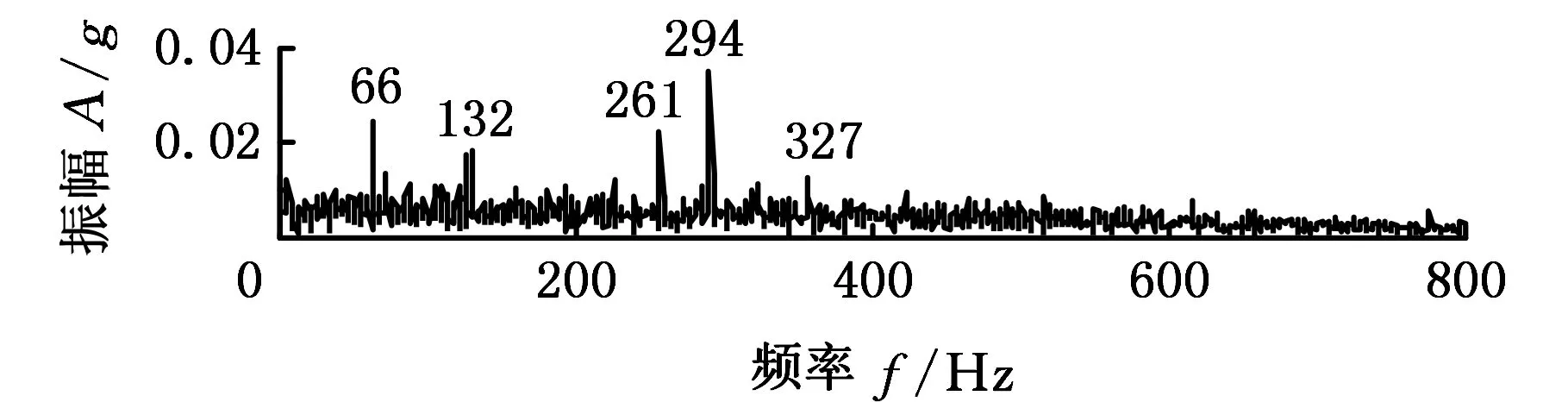
(d)嚴重損傷圖7 不同狀態下包含主要故障信息 的IMF分量全矢包絡譜Fig.7 Full vector envelope spectrum of IMF component consisting main fault information in different condition

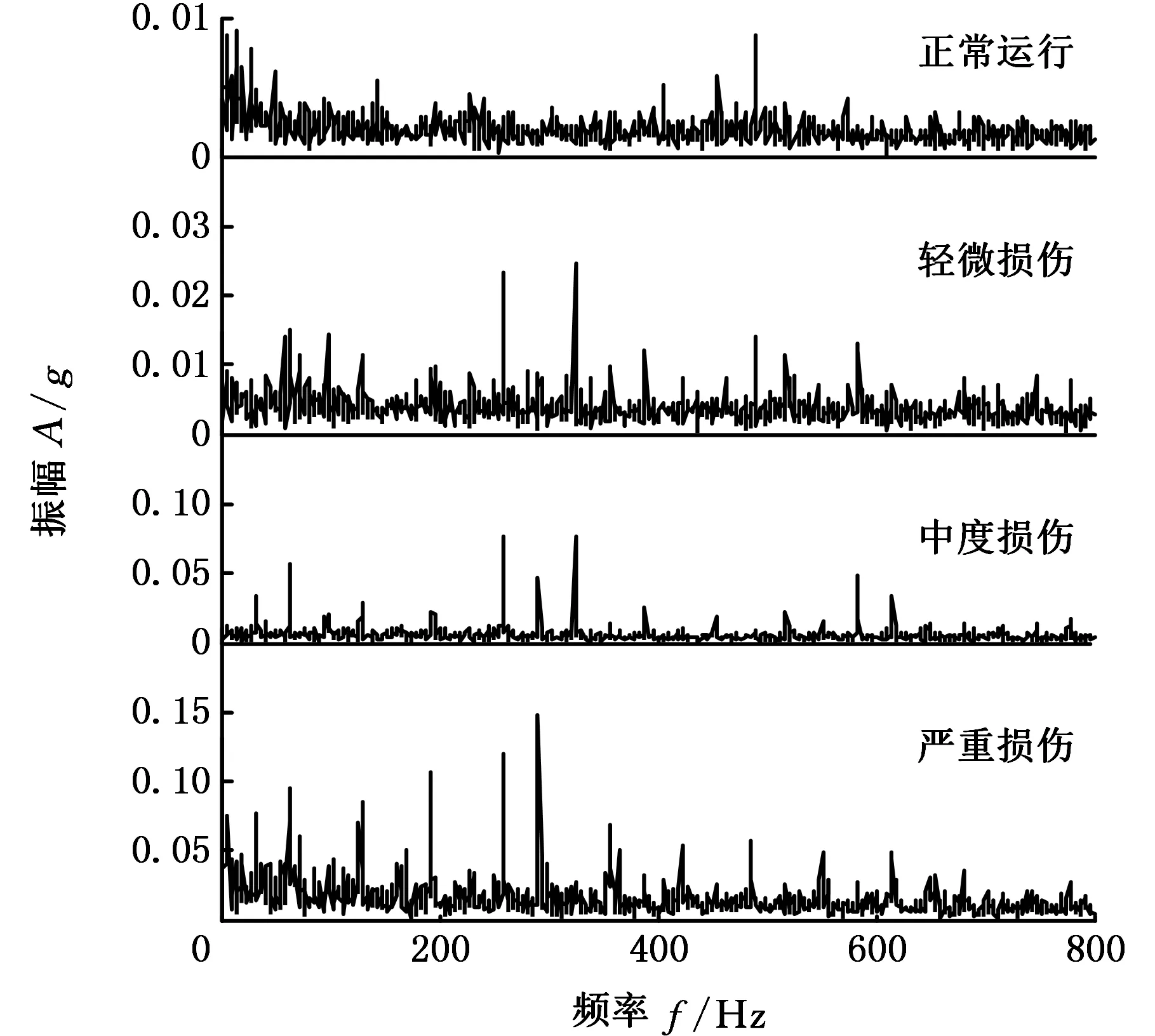
圖8 原始信號全矢包絡譜Fig.8 Full vector envelope spectrum of original signal

4 結論

(1)將不同狀態下的多通道振動信號用MEMD分解后，可得到相同階數的IMF分量，且同階的頻率成分一致。利用互相關系數準則選取的最敏感IMF分量可在一定程度上代表原始信號的故障信息。

(2)仿真分析和實例分析表明，隨著故障程度的增大，包含主要故障信息的IMF分量的頻譜結構變得復雜，且呈現出了一定的規律性。

(3)和傳統的全矢包絡分析相比，利用互相關系數準則選擇出的IMF分量的全矢MEMD包絡分析能明顯表征滾動軸承在正常、輕微故障、中等故障、嚴重故障時的頻譜結構，其變化更能準確、全面地反映滾動軸承性能的退化。

[1] 楊曉蔚，周宇. 滾動軸承重要性與技術含量縱論[J]. 軸承，2003(1)：35-38. YANG Xiaowei, ZHOU Yu. Importance of Rolling Bearing and Review of Technical Content[J]. Bearing, 2003(1)：35-38.

[2] ZHAO Xiaomin, PATEL T H, ZUO Ming J. Multivariate EMD and Full Spectrum Based Condition Monitoring for Rotating Machinery[J]. Mechanical Systems and Signal Processing, 2012，27(1):712-728.

[3] REHMAN N, MANDIC D P. Multivariate Empirical Mode Decomposition [J]. Proceeding of Royal Society A，2010，466:1291-1302.

[4] 顏云華，吳志丹. 基于MEMD的高速列車轉向架故障的排列熵特征分析[J].電子技術應用，2016，42(5)：124-127. YAN Yunhua, WU Zhidan. Feature Analysis of High-speed Train Bogie Based on MEMD and Permutation Entropy[J]. Application of Electronic Technique, 2016, 42(5):124-127.

[5] 張兵，于淑靜，董紹江. 基于譜峭度和多元經驗模式分解的機械故障診斷[J]. 制造技術與機床，2015(6)：97-101. ZHANG Bing, YU Shujing, DONG Shaojiang. Mechanical Fault Diagnosis Using a Hybrid Spectral Kurtosis and Multivariate Empirical Method Based on Mode Decomposition[J]. Manufacturing Technology & Machine Tool, 2015(6):97-101.

[6] 武哲，楊紹普，任彬，等. 基于噪聲輔助多元經驗模態分解和多尺度形態學的滾動軸承故障診斷方法[J]. 振動與沖擊，2016，35(4)：127-133. WU Zhe, YANG Shaopu, REN Bin, et al. Rolling Element Bearing Fault Diagnosis Method Based on NAMEMD and Multi-scale Morphology[J]. Journal of Vibration and Shock, 2016, 35(4):127-133.

[7] 韓捷，關慧玲，梁川，等. 矢譜：一種實用的旋轉機械故障診斷分析方法[J].機械強度，1998，20(3)：212-215. HAN Jie, GUAN Huiling, LIANG Chuan, et al. Vector Spectrum:a Practical Analysis Method of the Rotary Machine Fault Diagnosis[J]. Journal of Mechanical Strength，1998，20(3)：212-215.

[8] 韓捷，張錢龍. 全矢譜技術在WTDS實驗臺故障診斷中的應用[J].鄭州大學學報(工學版)，2017，38(1)：74-77. HAN Jie, ZHANG Qianlong. The Application of Full Vector Spectrum Technology in Fault Diagnosis of WTDS Experimental Platform[J]. Journal of Zhengzhou University (Engineering Science), 2017, 38(1):74-77.

[9] 李凌均，陳超，韓捷，等. 全矢支持向量回歸頻譜預測方法[J]. 鄭州大學學報(工學版),2016,37(3):78-82. LI Lingjun, CHEN Chao, HAN Jie, et al. The Prediction Method of Frequency Spectrum Based on Full Vector Support Vector Regression[J]. Journal of Zhengzhou University (Engineering Science), 2016, 37(3):78-82.

[10] 韓捷，石來德. 全矢譜技術及其工程應用[M]. 北京：機械工業出版社，2008. HAN Jie, SHI Laide. Full Vector Spectrum Technique and Its Application in Engineering[M]. Beijing:China Machine Press, 2008.

[11] 吳斌，王敏杰，康晶，等. 滾動軸承故障振動信號特征與診斷方法[J].大連理工大學學報，2013，53(1)：76-81. WU Bin, WANG Minjie, KANG Jing, et al. Fault Vibration Signal Feature of Rolling Bearing and Its Diagnosis Method[J]. Journal of Dalian University of Technology, 2013, 53(1):76-81.

(編輯 張 洋)

Study on Frequency Spectrum Structure for Rolling Bearing DegradationBased on Full Vector Fusion and MEMD

MA Yanli JIN Bing ZHANG Xuexin HAN Jie

Research Institute of Vibration Engineering,Zhengzhou University,Zhengzhou,450001

In order to recognize degradation processes of rolling bearings, a method combined MEMD with full vector fusion was proposed. Firstly, multi-channel synchronous analyses of vibration signals in different conditions were dealt with MEMD to obtain a series of multivariate intrinsic mode function(IMF) component. Then the most sensitive IMF component was selected by cross-correlation coefficient criterion to do full vector envelope analysis for extracting signal features. Analysis with simulated signal and actual signal was done to test effectiveness of the method respectively. It indicates that the method may reveal changes of frequency structure when faults appear, and shows the regularity that the more serious of the fault conditions is, the more complex of frequency spectrum structure becomes.

multivariate empirical mode decomposition(MEMD); full vector fusion; frequency spectrum structure; bearing degradation

2016-06-07

TH133.3

10.3969/j.issn.1004-132X.2017.14.019

馬艷麗，女，1991年生。鄭州大學機械工程學院碩士研究生。主要研究方向為設備故障機理及智能診斷技術。E-mail:1076065749@qq.com。金 兵，男，1990年生。鄭州大學機械工程學院碩士研究生。張學欣，男，1989年生。鄭州大學機械工程學院碩士研究生。韓 捷，男，1957年生。鄭州大學機械工程學院教授、博士研究生導師。