互依變量分析在體育管理研究中的應用

Jerry J．Wang，Kevin K．Byon，James J．Zhang，安俊英

(1．美國西佐治亞大學體育管理、健康與教育系，佐治亞州卡羅頓30116;2．美國印第安納大學運動學系，印第安納州伯明頓47405; 3．美國佐治亞大學國際體育管理研究中心，佐治亞州雅典30602;4．上海體育學院經濟管理學院，上海200438)

互依變量分析在體育管理研究中的應用

Jerry J．Wang1，Kevin K．Byon2，James J．Zhang3，安俊英4

(1．美國西佐治亞大學體育管理、健康與教育系，佐治亞州卡羅頓30116;2．美國印第安納大學運動學系，印第安納州伯明頓47405; 3．美國佐治亞大學國際體育管理研究中心，佐治亞州雅典30602;4．上海體育學院經濟管理學院，上海200438)

介紹互依變量分析的統計程序與技術及其在體育管理研究中的應用，包括聚類分析、探索性因子分析、驗證性因子分析，并結合實證研究的設計逐步進行說明，為體育管理研究者提供“即學即用”的研究方法指南。

體育管理;類別分析;因子效度;建構效度;互依變量分析;聚類分析;探索性因子分析;驗證性因子分析

Author’s address1．Department of Sport Management，Wellness and Physical Education，University of West Georgia，Carrollton 30116，Georgia，USA;2．Department of Kinesiology，Indiana University， Bloomington 47405， Indiana， USA; 3．International Sports Management Research Center，University of Georgia，Athens 30602，Georgia，USA;4．School of Economy＆Management， Shanghai University of Sport， Shanghai 200438，China

在相依變量分析中，研究者需要對因變量/效標變量(DV)和自變量/預測變量(IV)進行區分，而本文介紹的互依變量分析并不區分DV和IV［1］。互依變量分析的主要目的是探索一組變量間的潛在結構，而不是利用一個或多個IV對DV進行解釋和預測。通常體育管理研究中的互依變量分析包括2種主要類型:Q分析和R分析［1-2］。Q分析旨在根據觀測對象某些特征的相似性形成結構或分組，如聚類分析;R分析則根據一組變量的變量間相關系數生成結構或分組，如探索性因子分析(exploratory factor analysis，EFA)和驗證性因子分析(confirmatory factor analysis，CFA)。

1 聚類分析

聚類分析被廣泛應用于消費者市場細分研究，對消費者按照背景、心理、行為和(或)生活方式的同質性特征進行分組，算法保證每個聚類具有很高的內部同質性和外部異質性(不同聚類間)［3］。在聚類分析中，同質性和異質性通常是以距離進行評價，這有別于傳統的因子分析，因子分析的評價標準是模式的相似性和變異性(即相關性水平)。在選擇生成聚類的數量上，如果越多的聚類生成，聚類內部的同質性就會越大，聚類間的異質性也相應增大，然而這也會導致更復雜的模型。因此，研究者需要依據課題的具體情況平衡聚類的同質性和模型的復雜度。聚類的最佳數量需要根據統計結果的穩健性、概念原理以及研究的實用價值進行綜合判斷。

總體而言，聚類技術和過程包含2種通用的數學算法:分層聚類算法［4］和劃分(分離)聚類算法［5］。對于分層聚類算法，算法運行之前研究人員并不知道有多少聚類會從收集到的數據中產生，因此有時識別聚類的數量也是研究的目的之一。為了實現這一目標，研究者必須具備很強的概念和理論水平，而不僅僅依賴大樣本數據算法分析的結果。具體的算法是，首先測量觀測對象在某些變量上的相似性，最常見的相似性測量是每一對觀測對象之間的歐氏距離，即2個數據點之間的直線距離的測量［3］，越小的歐氏距離代表越高的相似性。生成聚類時需要每次合并最近距離的2個觀測對象或對象聚類，并重復進行以形成不同的分層，直至完成最后2個聚類的合并。分層過程可以利用一些主流的統計軟件，如SPSS、SAS等自動完成，形成具體的分層結果和聚類方案。同時，數據分析所產生的樹狀圖可更直接地顯示每個聚類及相關距離。在水平型(垂直型)樹狀圖中，縱(橫)軸代表了具體的觀測對象，橫(縱)軸代表聚集系數。

對于劃分聚類算法，研究人員在數據分析前已確定了生成聚類的數量。K-means聚類是這一類算法的代表，具體的算法是，研究人員首先根據相關文獻和研究背景確定生成聚類的數量K，然后以每個聚類中所有觀測對象的均值作為質心進行聚類運算(初始時，可任選K個觀測對象作為質心)。在每一輪聚類運算中，計算出每個觀測對象對K個質心的歐氏距離系數，并根據最小距離重新對觀測對象進行劃分，不斷重復這一過程直至聚類模型收斂為止。K-means聚類算法快速簡單，更適合于處理大樣本的數據集。為了克服K-means聚類的缺點(如聚類數量K必須提前給定)，研究人員需要依據相關理論確定K的取值。并且，當同時存在多個解決方案時，建議基于解決方案多次運行 K-means聚類算法以得到一個最優的聚類模型。

實證舉例:在文獻［6］中對體育彩票消費的研究中，研究者試圖依據體育彩票消費者的消費模式和人口統計信息對其進行類型劃分［6］。此項研究的基本問題是從數據中發現彩民的類型是否真實存在并獲得彩民的聚類，而不是確定變量的結構，因此聚類分析被認為是最合適的研究方法。通過開展面對面的封閉式訪談，4 980名合格的受試者參加了該調查。他們在過去的12個月中至少購買過體育彩票1次。受試者被要求回答24項與體育博彩消費行為相關的問題，所有問題采用李克特5級量表編制，問卷同時測量受試者在體育彩票上的花費水平，并對每個受試者的人口統計信息進行收集。研究中對體育彩民的類型劃分基于現有的測量模型，參照文獻［7］中對“問題型博彩行為量表”的研究，研究人員在聚類分析之前對可能產生的聚類數量已有了大致的判斷［7］。具體而言，有3個潛在的聚類解決方案:3－聚類、4－聚類以及5－聚類。因此，應用K－means聚類算法實際的分析過程是執行SAS軟件中的PROC FASCLUS程序。統計結果顯示，5－聚類的解決方案是最合適的類型劃分模型。5－聚類解決方案的結果如表1所示。

表1 聚類分析－5聚類方案的組內和組間變異Table 1 Cluster analysis-between and within group variability of a five－cluster solution

如前所述，一個較小的歐氏距離代表更高的相似性。在表1中，每個觀測對象與其聚類質心之間的歐氏距離(即組內變異)小于聚類質心之間的歐氏距離(即聚類間變異性)，代表了所提取的5個聚類的統計學差別。非常重要的是，研究人員也同時從理論上評估K－means聚類形成的5－聚類方案的合理性。在證實了5－聚類模型的理論合理性之后，研究人員基于每個聚類的人口統計信息和彩票消費特征進行命名。這5個聚類分別命名為普通彩民、升級彩民、危險彩民、強迫癥彩民和賭癮彩民。作為聚類分析的結果，建立一個體育彩民的類型劃分，為相關的營利和非營利組織制定干預計劃提供診斷參考。

2 探索性因子分析(EFA)

EFA是體育管理研究中使用最多的一種多元統計方法。EFA的主要目的:①確定一組變量背后潛在的因子結構和數量;②通過將高度相關的變量集聚在一起精簡數據。其對一組變量中相關性較強的變量進行歸納，生成一個簡約并具有代表性的變量結構。這種變量結構可以用來代表理論中的抽象的概念(latent construct)，即該概念無法被直接測量，而只能間接地對相關的可觀測變量進行評估。使用這種方法一般要求變量是連續變量，在一些特殊的估計中，EFA也可以處理類別變量［8］。EFA的分析步驟如下:

(1)評估樣本大小。雖然對于樣本的大小沒有嚴格的規定，經驗規則是樣本容量與變量數量的比例最低達到5∶1，達到10∶1以上是比較理想的［1］。

(2)檢驗概念假設和統計假設的適當性。概念假設是指反映變量間潛在結構的理論原理，而統計假設是指變量間是否統計相關，相關性評估的標準有2個:①巴特萊特球形檢驗(BTS)是一種檢驗各個變量之間相關性程度的方法。它利用變量的相關系數矩陣判斷變量是否適合用于做因子分析。統計上顯著的BTS意味著變量的相關系數矩陣不是相同的，揭示了這些變量之間存在相關性。② Kaiser－Meyer－Olkin (KMO)檢驗是一種反映變量間整體相關程度的統計指數，旨在檢查樣本容量是否適合進行因子分析。一般而言，KMO的度量標準是:0．9以上表示非常適合; 0．8表示適合;0．7表示一般;0．6表示不太適合;0．5以下表示極不適合［1］。

(3)選擇因子提取方法。考慮到因子分析是建立在所有變量之間的相關系數矩陣上，研究人員需要計算出一個變量的方差中與其他變量共享的部分(即公共方差，可以通過公因子方差衡量)、不能被共享的部分(即獨特方差)以及測量誤差造成的部分(即誤差方差)。對于高度相關的變量，變量之間的公共方差(或公因子方差)相應較高，同時獨特方差相應較低。在EFA中，研究者感興趣的是變量之間的公共方差，并試圖根據公共方差確定這些變量代表的潛在維度。此外，還存在另一種因子分析方法稱為主成分分析法(PCA)，其目的是用少數幾個主成分從數據中抽取最大的總方差。雖然2種因子分析方法有類似的操作程序，但具體采用哪種分析方法應根據研究的目的進行合理選擇。如果已知變量的獨特方差和誤差方差相對總方差很小，采用PCA;相反，如果公共方差、獨特方差和誤差方差均未知，采用EFA則比較合適［1］。

(4)提取因子數量的標準。預先確定的因子數量應與研究目標和概念合理性相適應。采取3種通用的統計標準確定保留的因子數量:①Kaiser規則，保留特征值等于或大于1．0的因子;②所保留的因子至少能解釋所有變量60%的方差［1］;③碎石圖提供了因子數目和特征值的大小(圖1)。

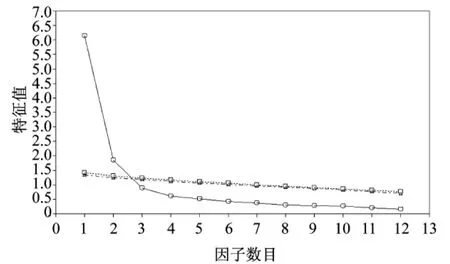
圖1 探索性因子分析碎石圖Figure 1． Screen plot in exploratory factor analysis

(5)因子旋轉。將因子的參考軸旋轉到某一位置，以減少含義不清的初始因子，并生成一個結構更簡單、更易解釋和理論上更有意義的因子解決方案。正交旋轉和斜交旋轉這2種旋轉方法被廣泛應用于體育管理研究中。對于正交旋轉，旋轉過程中軸必須保持90°正交，這種類型的主要方法包括:最大方差法(Varimax)，它簡化了因子矩陣的列;四次方最大值法(Quartimax)，它簡化了因子矩陣的行;相等最大值法(Equimax)，它同時簡化了因子矩陣的行和列。對于斜交旋轉，旋轉軸可以處于小于90°的理想位置。一些常見的斜交旋轉方法包括直接斜交法(Oblimin)、Geomin法和最優轉軸法(Promax)。Promax旋轉同時結合了最大方差法(正交)和斜交旋轉的技術［9］。在選擇合適的旋轉方法上，研究人員需要綜合考慮具體的理論框架、數據特點和相關文獻的研究結果［10］。

(6)決定保留的題項(變量)。有3種規則適用于這一過程:因子載荷的統計顯著性、交叉或雙因子載荷以及因子包含的最優題項數。對于因子載荷，樣本容量很大時可以相應地降低對因子載荷的要求。為保證因子載荷的顯著性，不同的因子載荷水平下樣本大小的最低要求如下:① 0．30最低樣本容量 350;②0．35最低樣本容量250;③ 0．40最低樣本容量200;④0．45最低樣本容量150;⑤0．50最低樣本容量120。對于交叉因子載荷，不保留具有交叉因子載荷的題項。在此交叉因子載荷是指一個題項同時在2個或以上的因子上具有中度到高度的載荷。對于因子包含的最優題項數，每個因子中至少保留3個題項是合適的［1］。從EFA中得到的因子應作為CFA的前導研究，并作進一步分析，CFA是一種理論驅動的因子處理方法［11］。

實證舉例:文獻［12］中檢驗了球迷對專業團隊運動核心質量的感知(即比賽水平)，它被概念化為對體育賽事核心特征的市場需求［12］。為了準確地理解球迷對專業團隊運動的市場感知需求，研究者開發了評估專業團隊運動核心特征的市場需求量表(Scale of Market Demand，SMD)。①通過廣泛的文獻回顧、田野調查以及針對專業隊營銷經理的訪談，確定市場需求的指標體系。SMD包含的所有題項綜合考慮了專業團隊運動獨特的產品和服務特性。由此，SMD的初始版本中共有46個題項，包含主隊、客隊、運動特征、觀賽成本、比賽促銷、方便安排等子維度。② 所有題項采用李克特5級量表編制，通常在心理測量中李克特5級量表被視為連續變量。通過在不同的體育賽事現場調查和社區攔截填寫問卷等方式收集數據，回收453份有效問卷用于數據分析，它們被隨機分成兩半，其中一半進行探索性因子分析。樣本量略微超過5∶1的比例(即樣本量與測量指標的比例)。

使用選定的數據集，利用EFA從SMD的題項中獲得一個簡單的結構［13］，EFA采用最優轉軸法Promax進行α因子提取［14］。EFA分析的主要目的是識別市場需求概念的潛在結構，實現從樣本變量到通俗變量(被命名)的概念一般化，同時也可以把大量的題項減少至一個小得多的、易處理的因子集合。利用以下4個標準確定因子和其包含的題項:①因子特征值等于或大于1．0［15］;②題項因子載荷等于或大于0．4，且不存在雙重載荷［16］;③一個因子至少包含3個題項［1］;④因子和題項的保留必須有理論依據。此外，碎石圖也被用于幫助決定提取因子的數量［17］。

分析結果如下:樣本充足率指標KMO的取值為0．845，大于閾值0．70，表明公共方差的水平良好，該樣本量適合進行因子分析［15］。巴特萊特球形檢驗BTS為4 521．27(P＜0．001)，變量的方差和協方差矩陣是一個單位矩陣的假設被拒絕，因此因子分析被認為是適當的。通過EFA，從31個題項中提取了6個因子，能解釋變量57．69%的方差。從生成的碎石圖看，也支持6因子模型的結果。根據預先設定的標準，題項的因子載荷小于0．4的9個題項被淘汰(它們是高水平表現、主隊的明星球員、支持主隊、高水平的技能、天氣條件、勢均力敵、客隊的對抗、比賽激烈程度和座位的優勢)。

另外，6個題項被移除，因為只有1個或2個題項被加載到相應的因子(它們是主隊破紀錄的表現、團隊競技、最好的球員在場上、球館的位置、熱愛專業團隊運動、專業團隊運動的流行程度)。最后，包括31個題項的6個因子被命名為:客隊(9題項)、主隊(6題項)、比賽促銷(5題項)、觀賽成本(4題項)、運動特征(4題項)、方便安排(3題項)。解析后的因子結構總體符合本文研究中SMD量表的概念模型。EFA保留的題項將用于后續的CFA，將在下一節中介紹。通過Promax旋轉后得到的系數矩陣如表2所示。

3 驗證性因子分析(CFA)

通過上面的EFA，得到了一個簡單的因子結構，通常它被認為是一個初步的結果，因為僅僅從數據樣本中提取因子使得測量模型缺乏理論基礎。盡管在EFA中也利用理論選擇題項或變量、確定潛在的因子和給因子提供理論解釋，但因子仍在很大程度上取決于一個研究樣本。通常情況下，一個EFA中得到的因子結構可以作為CFA的前導研究，CFA被認為是一種相對由理論驅動的驗證方法［1］。故CFA已成為一種常規的應用于心理特征觀測的統計方法。

若進行CFA需要以下5個步驟:(1)模型設定。

式中，p是模型中觀測指標的數量。如果有4個觀測指標，協方差矩陣會產生指標變量獨特方差和協方差信息，即4個獨特方差和6個協方差。

(3)模型估計。需要將獨特方差和協方差的數量與模型需要估計的參數數量進行比較:如果前者小于后者，則被認為是不可識別的模型。即獨特的方差和協方差的數量太少以至于不能估計模型;如果2個數字相等，那么該模型被稱為恰好識別，因子模型的自由度為零，即只存在一個模型估計的結果;如果前者大于后者，那么因子模型被過度識別，模型估計的自由度大于零。前2種都不是模型估計的理想情況，研究人員需要努力構造一個過度識別的因子模型。如果一個模型只有一個潛在的因子，則潛因子至少有3個指標(每個指標均包含與指標相關的誤差項)不相關才能保證模型是過度識別的。

除了識別問題，其他因子分析的一般規則也適用于CFA，比如不能有交叉載荷的指標以及一個因子至少有3個測量指標。因為CFA涉及潛在的因子，它不能觀察到或直接測量，所以使用多個可觀測指標捕捉潛在因子的方差。此外，增加更多的觀測指標能增加因子過度識別的程度以及因子的可靠性，進一步提高測量模型的估計質量。在EFA中的建議樣本容量也可用于確定CFA的樣本大小。即至少應達到樣本容量與指標數量的比例5∶1，并努力實現10∶1的比例。

(4)模型擬合優度檢驗。研究人員需要評估測試模型對數據集的擬合優度。以下是一些體育管理研究中在評估測量模型的擬合優度時被廣泛采用的一般指數:

①正態卡方值(Normed Chi－square)。該指標是計算出一個卡方自由度比。鑒于卡方值隨著樣本容量的增加而膨脹，有必要計算一個加權的指數。即便如此，正態卡方值在樣本容量很大時依然取值較大。一般而言，樣本小于750個時，正態卡方值小于3．0表示模型具有好的擬合度［1，18］。基于理論構造模型的潛在因子結構和相關的觀測指標。

(2)模型識別。檢查模型是否可識別，即樣本協方差矩陣是否提供了足夠的信息形成一個測量模型。變量的獨特方差和協方差的數量N可以通過以下公式計算:

表2 市場需求量表的因子系數矩陣Table 2 Factor pattern matrix for the scale of market demand variables

② RMSEA指數(Root Mean Square Error of Approximation)。RMSEA的取值表示模型在多大程度上符合總體，因此該指數對樣本大小不敏感。RMSEA值越小表示模型擬合度越好。一般而言，RMSEA值小于0．6表示好，在0．6～0．8表示一般，大于0．8表示差［19-20］。

③CFI指數(Comparative Fit Index)。CFI用來評估擬建模型和零假設模型的適合度［21］。它的一個突出的優點是對因子模型的復雜度不敏感［1］。一般而言，CFI值大于0．90表示較好的擬合度［19］。

④SRMR指數(Standardized Root Mean Residual)。每個協方差的估計誤差會產生殘差。SRMR指數是平均標準化的殘差。其值在0．0～1．0變化，值越小表示模型擬合度越好。一般而言，SRMR＜0．08表示一個可接受模型擬合度水平［19］。

除了評估因子模型的擬合優度指標，構建測量模型的效度與信度也需要進一步檢查。主要包括3種類型:聚合效度;區分效度;理論效度。聚合效度是指構成因子的多個指標共享方差的比例，它通常是由3個指標進行評估，包括標準化因子載荷、平均方差提取(AVE)和建構信度(CR)［1］。其中:① 標準化因子載荷代表一個指標的公因子方差。標準化因子載荷的平方就是能被該指標解釋的因子方差的多少。理論上建議一個指標應解釋50%或更多的一個因子的方差，即標準化因子載荷應大于0．70，至少達到0．50或更高。② 平均方差提取(AVE)是聚合效度的另一個重要指標，它表示一個指標的因子載荷提取因子方差的平均值［1］。根據這個定義，AVE的值可以通過下式計算:

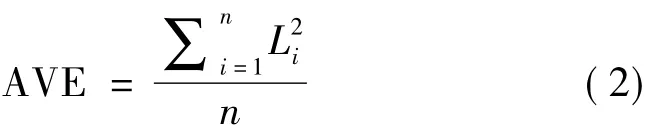
一般來說，建議AVE的值達到0．50或更高。③建構信度CR是指標因子載荷的平方總和與指標總方差的平方之和的比例，可以用以下公式計算:

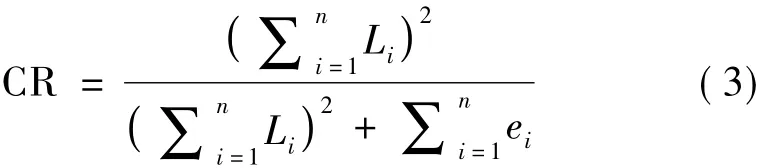
式中:Li是指標i的標準化因子載荷;ei是誤差方差。一般來說，CR值在0．60～0．70表示一個可接受的水平，高于0．70表示較好的可靠性。

區分效度是指一個潛在因子在多大程度上與其他因子存在差異［22］。通常采用皮爾遜相關系數評估2個因子的區分效度。根據經驗法則，因子間相關系數小于0．85表示一個可接受的區分效度水平［18］。更嚴格的評估區分效度是將AVE與潛在因子的平方相關進行比較。Fornell等［23］建議因子之間的平方相關必須低于任何一個因子的AVE值。理論效度是檢驗在多大程度上當前目標因子與其他相關理論形成的因子之間存在相關性［24］。顯著的相關性將支持提出的測量模型的理論合理性，其評估既包括采用相關標準做概念內部的判斷，也包括獨立于測量概念的預見性標準。此外，克倫巴赫系數α常被用來評估提出的因子模型的信度，它表示一組指標在多大程度上存在相關性［25］，可以通過下式計算:

其中，α介于0．0～1．0。克倫巴赫系數α越大表示模型信度越好。一般而言，克倫巴赫系數α的值應該達到0．70或更高［18］。

(5)模型修正。如果這些指數低于建議的標準，研究人員需要通過修正指數修改模型及其包含的因子和題項，修正指數則基于因子結構中未指定的相互關系計算，修正指數的計算程序通常包含在Mplus和AMOS等統計軟件包中。需要注意的是，修改因子模型不僅基于實證方面(如因子載荷)，也要以理論作為基礎。CFA的具體操作步驟見實證研究案例。在實踐中，當從數據中得到多個可能的因子結構方案時，需要進一步比較不同模型的擬合優度、效度和信度、理論的合理性以及遵從精簡原則等進行選擇。

實證舉例:前面已經使用文獻［12］的研究說明EFA的用法，這里繼續用它說明CFA的使用程序。在此案例中，執行AMOS的CFA程序對前面EFA中保留的SMD因子進行最大似然估計(ML)，將另一半數據集提交給 CFA程序，對一個包含31題項的6－因子測量模型進行ML估計，擬合優度指數顯示6－因子測量模型對數據的擬合度不佳，正態卡方值(χ2/df=3．20)高于建議截止值(＜3．0)，表示擬合度差。RMSEA值也顯示 6－因子模型擬合度差(RMSEA=0．10，90%CI=0．094－0．106)。雖然SRMR值(0．08)在可以接受的范圍內(≤0．10)，而CFI值(0．78)大大低于推薦截止值(＞0．90)，也表示模型對數據的擬合度不佳，擬合度檢驗的總體結果是建議修改或重新設定模型。文獻［26］中也建議在模型對數據的擬合度不佳時，模型應該重新被設定［26］。在當前的分析中，指標載荷范圍從0．398 (團體票成本)到0．903(廣告)。在31個題項中，有9項指標載荷低于0．707，表明這些指標的誤差方差大于它們的共享方差。因此，這9項指標(即客隊歷史傳統、主隊士氣、網絡信息、旅行距離、比賽觀賞性、比賽速度、團體票成本、比賽持續時間、主隊歷史傳統)被刪除。此外，修正指數表明擬合度問題與其他5項指標(即客隊明星球員、主隊球員整體水平、客隊聯賽積分排名、宣傳、客隊球員的個人魅力)有關，這5個指標存在嚴重的雙重因子載荷問題，雙因子載荷系數的范圍為0．50～0．60，表明單個指標不止在一個因子上負有載荷。通過仔細審視這些統計判斷，最后決定把以上14個題項從模型中刪除。

在對模型進行重新設定后，得到一個包含17個題項的5－因子模型:主隊(3題)、客隊(5題)、比賽促銷(3題)、觀賽成本(3題)、方便安排(3題)。利用CFA對新的5－因子模型進行分析。擬合優度指數顯示5－因子模型對數據的擬合度非常好。正態卡方值(χ2/df=2．55)低于建議的截止值(＜3．0)，RMSEA值也表明5－因子模型的擬合度可以接受(RMSEA= 0．084，90%CI=0．072～0．096)，SRMR(0．054)的值非常好(≤0．10)，CFI(0．92)被認為是可以接受的。總體來看，5－因子模型的擬合優度大幅改善，表示該模型比6－因子模型有更好的可接受性(表3)。因此，選擇5－因子模型作進一步的研究。

表3 6－因子模型和5－因子模型的擬合優度指標Table 3 Goodness-of-fit indexes of six-factor model and fivefactor model

接下來，對5－因子模型進行信度分析。5－因子模型的各個因子和題項的信度評估采用 CR(閾值0．70)和AVE(閾值0．50)進行。如表4所示，5個因子的CR值范圍從0．76(觀賽成本)到0．82(客隊，比賽促銷)。

表4 5－因子模型的因子載荷(λ)、建構信度(CR)、平均方差提取(AVE)Table 4 Factor ladings(λ)、construct reliability(CR)、and average variance extracted(AVE)for the fivefactor model

此外，所有因子的AVE值高于建議的標準，從0．52 (觀賽成本)到0．64(客隊)。基于信度檢驗的整體信息，確定各個因子是可靠的。所有指標的載荷是統計顯著的，z分數從8．99到16．79(P＜0．05)。此外，除了主隊聲譽(0．60)和每周比賽日的安排(0．67)外，所有指標的載荷大于建議的標準0．707［27］。決定保留這2項的原因是其在理論上與主隊和方便安排2個因子聯系緊密，且取值上只略低于閾值0．707。總體而言，5－因子SMD模型具有一個簡單緊湊的結構。

模型中不存在因子間相關系數大于0．85的情況，取值范圍從0．19(比賽促銷與觀賽成本之間)到0．51 (觀賽成本與方便安排之間)，表明SMD因子具有可接受的區分效度。同時，Fornell等［23］的測試發現，所有因子的平方相關均低于每個因子的AVE值，說明模型具有很好的區分效度。總體而言，基于上述2個CFA的結果分析，包含17題項的5－因子模型被認為是最合適的測量專業團隊運動的市場需求量表(SMD)。

4 討論

相對EFA而言，盡管近年來學術論文中CFA的使用穩步增加，但學術界關于EFA和CFA使用的爭論從未停止過。誠然，CFA似乎是一個更受歡迎的統計方法(鑒于CFA的理論驅動與EFA的數據驅動)，因此得到研究人員的青睞，甚至是一些審稿人在背后“推波助瀾”。然而，將CFA凌駕于EFA之上顯然言過其實，EFA和CFA作為相互依存的分析工具各有其優點。關于“CFA和EFA之間哪種方法更好”的問題，答案是兩者都很重要，使用則取決于具體的研究問題。EFA的主要目標是識別模型的潛在結構，而CFA的主要目標是驗證假設模型的潛在結構。因此，不建議在沒有適當理由的情況下，采用EFA測試先驗的假設模型。

在此澄清一些在EFA和CFA使用中出現的疑問。在許多使用CFA進行模型構建和驗證的研究中，模型的再指定往往是利用修正指數。首先，盡管CFA中包含了幫助研究者進行模型擬合度改進的程序(如修正指數和規范檢索)，但是一旦對原模型進行修正，這一過程將被認為不再是驗證性而是探索性，因為模型的再指定改變了建立模型的初始假設［28］。當采用原始樣本對修正模型進行估計時，“自我驗證”(即直接把探索性因子分析的結果放到同一數據的驗證性因子分析中)問題就會出現，因為這不是理論驅動的模型檢驗，而是數據驅動的模型構建。同時由于CFA被認為是比EFA更嚴格的模型測試方法，這樣就比較難達到驗證理論的目標了。此外，體育管理研究中數據收集的過程可能不是完全隨機的，這就意味著樣本不能真正代表總體，也會導致CFA分析的模型不被數據支持。因此，在利用指數進行模型修正時必須特別謹慎。由于有證據表明可能產生“自我驗證”問題，采用獨立樣本對修正模型的估計結果與采用原始樣本估計的結果會不一致［29］。建議的程序如下:① 建立先驗的假設模型;②采用CFA對模型進行估計;③當模型不被支持時，優先考慮基于理論修改模型，然后才是利用修正指數修改模型(即理論和指數結合起來使用);④采用獨立樣本重新估計修正后的模型。

另一類體育管理文獻中常見的錯誤是在CFA和EFA分析中采用同一個樣本數據。由于“自我驗證”問題的存在，這種做法是完全錯誤的。利用EFA，研究者可以得到關于數據的全部潛在結構，當然這個結構沒有任何的理論基礎。因此，在EFA得到的模型之上，利用同樣的數據進行CFA只是一個數據驅動的模型估計而不是對先驗模型的驗證。如果一個EFA得到的模型被認為與理論相符，必須在CFA中采用新的數據集進行檢驗，以避免產生“自我驗證”的問題［28］。建議的程序(特別是在大樣本的情況下)是將數據分為兩半，一半用于EFA，一半用于CFA［12］。另一個建議是當構建模型過程是基于理論時，首先用CFA進行模型檢驗，如果模型不被支持，再采用EFA找出模型的“差異”。在這種情況下，EFA和CFA可以采用同一個數據，因為其本質還是探索性的過程。如果研究者需要確認最終的因子結構，還是需要在CFA中采用獨立的樣本數據［30］。

EFA和聚類分析的相似性在實踐中也會產生一些混淆。例如，2種方法都是探索性的和數據驅動的，目標都是探索數據集的潛在結構，并簡化該數據集。2種方法的本質區別是聚類分析關注研究對象的結構，EFA關注對自變量的分析。此外，2種方法的類別評價標準也不同。聚類分析采用距離評價聚類的同質性，而EFA采用變異(即相關系數)生成因子。盡管EFA和聚類分析都是數據驅動的方法，對研究樣本的選擇也影響最后的因子或聚類的結構。因此，為了保證因子或聚類的效度和信度，研究者必須盡可能地選擇具有代表性的樣本和注重最終模型的理論合理性。值得一提的是，聚類分析不僅用于對人的聚類(例如，觀眾、參與者和運動員)，同樣也適用于其他的研究對象，如體育組織、地理區域和社區等。

本文對3種互依變量的統計分析方法進行了逐一說明。聚類分析通常用于市場營銷或管理細分研究中，基于人口統計學、認知、情感、行為和生活方式等因素或變量對人群進行分類(如消費者、企業員工等)。探索性因子分析和驗證性因子分析是從大量的直接觀察指標中識別并確認因子結構和潛在變量的統計分析方法，是2種被廣泛應用的研究方法。雖然理論上可以應用因子分析對一個包含多個概念的模型進行因子評估，然而，較好的實踐準則是每次針對單一領域單一概念的一個或相關的多個因子進行因子分析，分析可能涉及認知、情感、動機或行為等領域。由于探索性因子分析和驗證性因子分析是當前在體育管理研究中定量檢驗一個測量或量表的建構效度的先決條件，故本文也為如何在體育管理研究中開發具有良好效度和信度的測量奠定了基礎。

［1］ Hair J F，Black W，Babin B J，et al．Multivariate data analysis［M］．Upper Saddle River，N J:Pearson Prentice Hall，2010:89－470

［2］ Basilevsky A T．Statisticalfactor analysis and related methods:Theory and applications［M］．Hoboken，N J: Wiley，2009:1－36

［3］ Everitt B，Landau S，Leese M．Cluster analysis［M］．London:Arnold，2001:10－89

［4］ Jain A K，Murty M N，Flynn P J．Data clustering:A review［J］．Acm Computing Surveys，1999，31(3):264－323

［5］ Kaufman L，Rousseeuw P J．Finding groups in data:An introduction to cluster analysis［M］．Hoboken，N J:Wiley，1990:37－49

［6］ Li H，Mao L L，Zhang J J，et al．Classifying and profiling sports lottery gamblers:A cluster analysis approach［J］．Social Behavior＆ Personality:An International Journal，2015，43(8):1299–1318

［7］ Li H，Mao L L，Zhang J J，et al．Dimensions of problem gambling behavior associated with purchasing sports lottery［J］．Journal of Gambling Studies，2012，28(1):47－68

［8］ Gorsuch R．Factor Analysis［M］．Hillsdale，N J:Erlbaum，1983:1－65

［9］ Fabrigar L R，Wegener D T，MacCallum R C，et al．Evaluating the use ofexploratory factor analysis in psychological research［J］．Psychological Methods，1999，4 (3):272－299

［10］ Pett M A，Lackey N R，Sullivan J J．Making sense of factor analysis:The use offactoranalysisforinstrument development in health care research［M］．Sage Publications，2003:85－164

［11］ Gerbing D W，Hamilton J G．Viability of exploratory factor analysis as a precursor to confirmatory factor analysis［J］．Structural Equation Modeling:A Multidisciplinary Journal，1996，3(1):62－72 ［12］ Byon K K，Zhang J J，Connaughton D P．Dimensions of general market demand associated with professional team sports:Development of a scale［J］．Sport Management Review，2010，13(13):142－157

［13］ Stevens J．Applied multivariate statistics for the social sciences［M］．Mahwah，N J:Lawrence Erlbaum，1996:325－381

［14］ Hendrickson A E，White P O．Promax:A quick method for rotation to oblique simple structure［J］．British Journal of Mathematical and Statistical Psychology，1964，17(1):65－70

［15］ Kaiser H F．An index of factorial simplicity［J］．Psychometrika，1974，39(1):31－36

［16］ Nunnally J C，Bernstein I H．Psychometric theory［M］．New York:McGraw－Hill，1994:23－98

［17］ Cattell R B．The scree test for the number of factors［J］．Multivariate Behavioral Research，1966，1(2):245－276

［18］ Kline R B．Principles and practice of structural equation modeling［M］．New York:Guilford，2005:7－25

［19］ Hu L T，Bentler P M．Cutoff criteria for fit indexes in covariance structure anaysis:Conventional criteria versus new alternatives［J］．Structural Equation Modeling:A Multidisciplinary Journal，1999，6(1):1－55

［20］ MacCallum R C，Browne M W，Sugawara H M．Power analysis and determination of sample size for covariance structure modeling［J］．Psychological Methods，1996，1(2) (2):130－149

［21］ Bentler P M．Comparative fit indexes in structural models［J］．Psychological Bulletin，1990，107(2):238－246

［22］ Campbell D T，Fiske D W．Convergent and discriminant validation by the multitrait－multimethod matrix［J］．Psychological Bulletin，1959，56(2):81－105

［23］ Fornell C，Larcker D．Evaluating structural equation models with unobservable variables and measurement error［J］．Journal of Marketing Research，1981，18(1):39－50

［24］ Churchill G A． Marketing research: Methodological foundations［M］．Chicago，IL:Dryden，1995:51－121

［25］ Cronbach L J．Coefficient alpha and the internal structure of tests［J］．Psychometrika，1951，16(3):297－334

［26］ Tabachnick B G，Fidell，L S．Using multivariate statistics［M］．New York:Harper Collins，2001:628－675

［27］ Anderson D R，Gerbing D W．Structural equation modeling in practice:A review and recommended two－step approach［J］．Psychological Bulletin，1988，103(3):411－423

［28］ MacCallum R C，RoznowskiM，NecowitzL B．Model modifications in covariance structure analysis:The problem of capitalization on chance［J］．Psychological Bulletin，1992，111(3):490－504

［29］ Williams L J． Covariance structure modeling in organizational research:Problems with the method versus applications of the method［J］．Journal of Organizational Behavior，1995，16(3):225－233

［30］ Braunstein J R，Zhang J J，Trail G T，et al．Dimensions of market demand associated with pre－ season training: Development of a scale for major league baseball spring training［J］．Sport Management Review，2005，8(3):271－296

Application of Interdependent Variable Analysis in Sport Management Research

Jerry J．Wang1，Kevin K．Byon2，James J．Zhang3，AN Junying4

The current article aims to introduce a comprehensive setof statisticalprocedures and techniques of conducting interdependence analysis in the context of sport management．As three majortypes，interdependenceanalysis，clusteranalysis，exploratory factor analysis，and confirmatory factor analysis are presented and discussed respectively，combined with the research design of empirical studies，as well as the step by step analytical instructions，which provides sport management researchers with the read－to－use guidance in research practice．

sport management; classification analysis;factor validity;constructvalidity; interdependentvariableanalysis; cluster analysis; exploratory factor analysis; confirmatory factor analysis

G80-05

A

1000-5498(2017)04-0041-08

2016-10-20;

2017-03-18

Jerry J．Wang(1986-)，男，河南洛陽人，美國西佐治亞大學助理教授，博士;Tel．:(706)201-7183，E-mail:wangjq817 @gmail．com

安俊英(1980-)，女，山西交城人，上海體育學院副教授，博士;Tel．:(021)51253275，E-mail:anjunying @sus．edu．cn

DOI10．16099/j．sus．2017．04．008