非正交多松弛系數軸對稱熱格子Boltzmann方法?

王佐 張家忠 王恒

(西安交通大學能源與動力工程學院,西安 710049)

非正交多松弛系數軸對稱熱格子Boltzmann方法?

王佐 張家忠?王恒

(西安交通大學能源與動力工程學院,西安 710049)

(2016年9月3日收到;2016年11月22日收到修改稿)

提出了一種模擬軸對稱熱流動的非正交多松弛系數格子Boltzmann(MRT-LB)模型.通過采用非正交轉換矩陣,建立了基于D2Q9離散速度的求解流場的MRT-LB模型和基于D2Q5離散速度的求解溫度場的MRT-LB模型.Chapman-Enskog分析表明,該模型可以恢復對應的柱坐標下的宏觀連續方程、動量方程和能量方程.與現有的軸對稱MRT-LB模型相比,本文采用的非正交轉換矩陣中含有更多的零元素,因而具有更高的計算效率.采用本文模型對幾種典型的軸對稱熱流動問題,包括熱Womersley流動、豎直圓柱體內的Rayleigh-Bénard對流和環形柱體內的自然對流進行了數值模擬,通過等溫線圖和流線圖以及定量數據的對比,驗證了本文模型的可行性和可靠性.并且數值模擬結果表明,相對現有模型,本文模型具有更好的數值穩定性和計算效率.

軸對稱熱流動,格子Boltzmann方法

1 引 言

軸對稱流動在換熱器、太陽能設備、電子器件冷卻等工業領域有著重要應用.近年來有許多文獻對軸對稱流動換熱現象進行了數值研究[1,2].格子Boltzmann(LB)方法作為一種新興的數值方法,由于其分子動力學背景,具有簡單高效、邊界處理簡單、并行性強等特點,在許多領域獲得了重要應用[3-5].其中單松弛系數模型格子Boltzmann(SRT-LB,也稱作LBGK)模型由于其實現簡單,具有最為廣泛的應用.近年來,具有更加合理的理論基礎的多松弛系數格子Boltzmann(MRT-LB)模型也取得了飛速發展[6,7].

截止目前已有大量研究致力于將LB推廣到軸對稱流動問題的研究.Halliday等[8]首先基于宏觀柱坐標下的Navier-Stokes(NS)方程提出了一種適用于軸對稱流動的LB模型.隨后,Lee等[9]發現Halliday等[8]的模型缺失了一些徑向速度相關項,不能正確恢復宏觀的柱坐標下的NS方程.為克服此缺點,Lee等[9]提出了一種新的軸對稱LB模型.此后,Reis和Phillips[10,11]對Lee等[9]的模型進行了部分改進.但這些模型中均存在梯度項,對梯度項采用差分方法處理,降低了模型的數值準確性和穩定性,破壞了LB固有的計算局部化特性.與前面幾個基于宏觀柱坐標下的NS方程推導的LB模型不同,Guo等[12]直接從描述柱坐標流動的Boltzmann方程出發,推導出了一種柱坐標下的LB模型.此模型不包含復雜的梯度項,且其實施流程幾乎與標準LB完全相同.Li等[13]從二維笛卡爾坐標下的標準LB模型出發,將宏觀柱坐標下的NS方程轉化為類似標準的笛卡爾坐標下的NS方程加入與徑向坐標r有關的多個源項的形式,并提出了針對此種形式宏觀方程的LB模型,詳細闡述了從標準LB模型出發構造軸對稱流動LB模型的過程.Zhou[14]的模型對Li等[13]的模型進行了改進.

以上模型均針對等溫流場,為發展非等溫的軸對稱LB模型,Peng等[15]提出了一種采用LB模型求解速度場,而采用二階差分方法求解溫度場的混合模型.然而,Huang等[16]指出,隨著對流作用的增大,對流項采用二階差分方法容易導致發散,并對此混合模型進行了改進.然而,采用混合模型在很大程度上喪失了LB簡單易行的優勢.Li等[17]提出了一種求解溫度場的雙分布LB模型,其基本思想與文獻[13]類似.Zheng等[18]提出了另一種與Guo等[12]的方法類似的更加簡單的LB模型.

上述軸對稱模型均采用LBGK,即單松弛系數(SRT)碰撞模型.在該模型中,所有的物理量的弛豫時間均假設相同,這顯然與實際的物理過程不符.2000年,Lallemand和Luo[6]提出了一種多松弛系數LB模型(MRT-LB),在該模型中,通過引入轉換矩陣和碰撞矩陣,用不同的松弛系數來表示流體系統中不同物理量的弛豫.與SRT-LB相比,MRT-LB顯然具有更加合理的理論基礎.事實上,大量的數值模擬結果表明,MRT-LB模型相對于SRT-LB模型具有更好的數值穩定性和邊界處理準確性[5].由于這些優點,MRT-LB模型先后被應用到流動傳熱[19]、多孔介質流動[20]、多相流[5]和微尺度流動等[21]領域.這些MRT-LB模型均求解二維笛卡爾坐標下流體相關問題.2010年,Li等[13]和Wang等[22]將MRT-LB模型推廣到軸對稱流動領域,幾乎同時提出了針對柱坐標下軸對稱流動的不同的MRT-LB模型.

現有的所有MRT-LB模型均建立在正交化轉換矩陣的基礎上,該矩陣通過Gram-Schmidt正交化方法獲得,相應的這些MRT-LB模型可稱作正交MRT-LB模型.然而,最近Premnath和Banerjee[23]以及Geier等[24]指出,Gram-Schmidt正交化方法并不是獲得轉換矩陣的惟一途徑,并且提出了一種適用于二維笛卡爾坐標流場的非正交MRTLB模型.隨后,Liu等[25]根據這一思想,進一步提出了一種適用于二維笛卡爾坐標下的溫度場的非正交MRT-LB模型.與現有的正交MRT-LB模型相比,非正交的MRT-LB模型中轉換矩陣具有更多的零元素,因而計算效率獲得一定程度上的提高[25].

基于前人的工作,本文提出了一種針對軸對稱熱流動的MRT-LB模型,該模型中流場和溫度場均采用非正交轉換矩陣,相較于現有的模型,本文模型中的轉換矩陣含有更多的零元素,這使得模型在保持數值穩定性良好的前提下其演化過程更加高效.

2 雙分布軸對稱MRT-LB模型

2.1 控制方程

柱坐標下的流動傳熱問題是一個三維問題,然而,當周向速度為零時,流動可簡化為二維問題,其控制方程為[12,17]

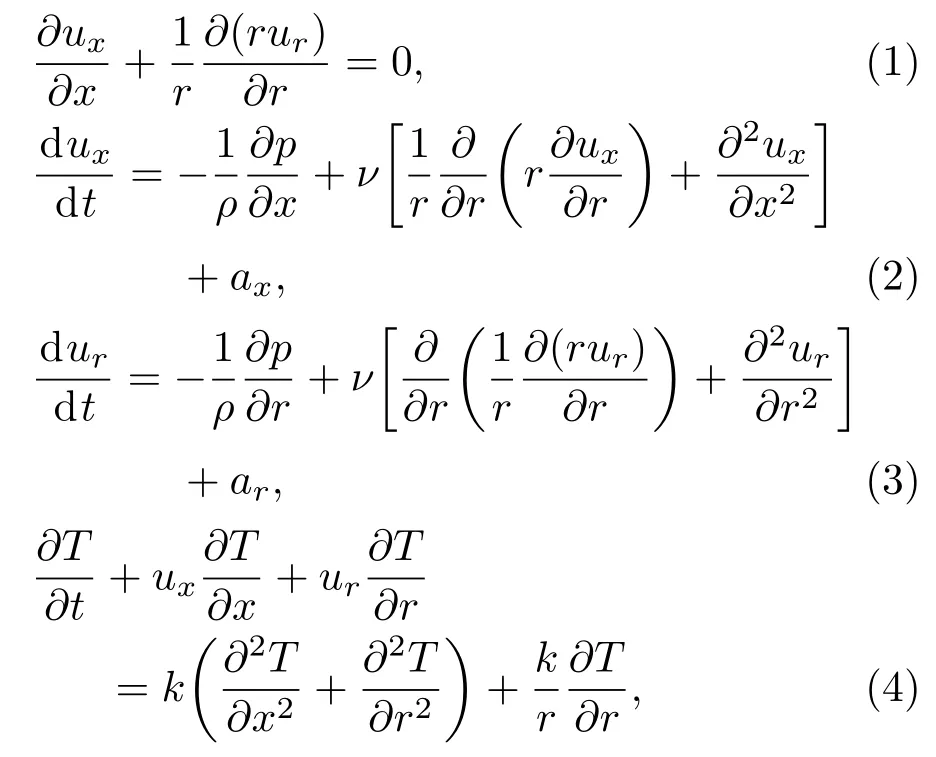
其中,x和r為分別為軸向和徑向坐標;ux,ur分別為軸向和徑向速度;ax,ar分別為軸向和徑向方向的外力;ρ為密度,T為溫度,ν為黏性系數,k為熱擴散系數.對于任意變量φ,

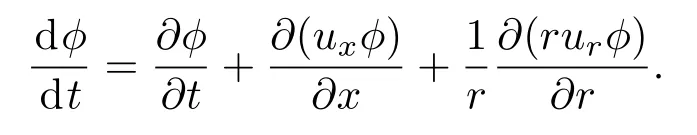
2.2 求解速度場的MRT-LB模型

格子Boltzmann方法通過描述具有離散速度的流體粒子分布函數的變化過程來反映流體粒子的運動過程.基于非正交轉換矩陣,本文提出一種適用于軸對稱流場的多松弛系數格子Boltzmann方法,其演化方程為

其中,f(x,t)為節點x在t時刻的密度分布函數;m和m(eq)分別為f和f(eq)對應的矩空間分布函數,其中f(eq)為密度平衡態分布函數;e為離散速度方向矢量;S=diag(s0,s1,s2,s3,s4,s5,s6,s7,s8)為松弛系數矩陣;δt為時間步長;M為轉換矩陣;I為單位矩陣;F為外力項.對于D2Q9離散速度模型,離散速度e為

轉換矩陣M為[23,25]

通過轉換矩陣可將粒子密度分布函數投影到速度矩空間.對于D2Q9模型,矩空間分布函數及其平衡態分布函數的計算如下：

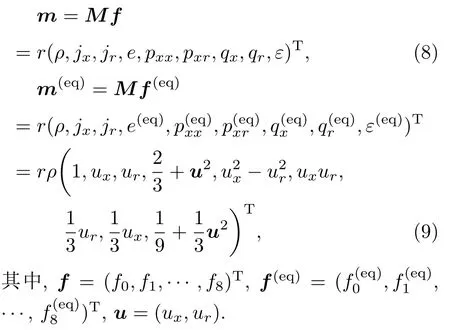
與現有的正交MRT-LB模型中通過Gram-Schmidt正交化方法得到的轉換矩陣不同,本文模型中采用的轉換矩陣的獲得無需采用Gram-Schmidt正交化過程[23-25],相應的MRT-LB模型可稱作非正交MRT-LB模型.顯然,與現有的轉換矩陣相比,本文模型中的矩陣具有更多的零元素,有望獲得更高的計算效率.

低Ma數條件下,平衡態分布函數可近似為

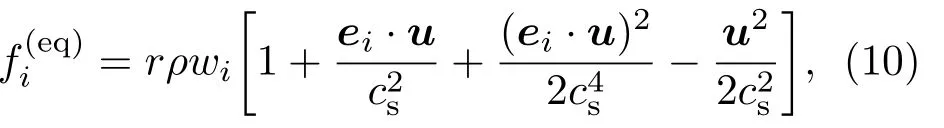
其中,w0=4/9,w1—4=1/9,w5—8=1/36,w5—8=1/36.為格子聲速,R和T分別為氣體常數和溫度.

外力項F可顯式的表示為

MRT-LB方法中分布函數的演化與LBGK模型類似,同樣可分為碰撞和遷移兩步,其中碰撞在矩空間進行,而遷移在速度空間進行：

碰撞

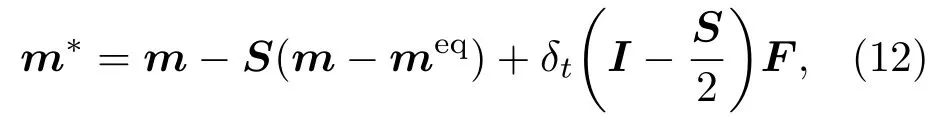
遷移

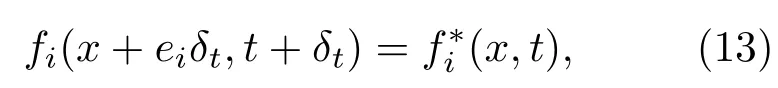
其中,碰撞后的分布函數f?=M-1m?,其中m?表示碰撞后的矩空間分布函數.

獲得密度分布函數后,宏觀量密度ρ、速度u和黏性系數ν可通過密度分布函數計算：

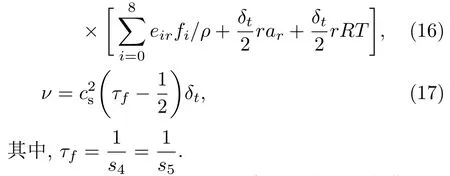
Chapman-Enskog多尺度分析表明,此模型可以準確恢復對應的宏觀柱坐標下的質量和動量守恒方程(見附錄A).

2.3 求解溫度場的MRT-LB模型

在LB方法中,二維的溫度場可以用D2Q4,D2Q5或者D2Q9離散速度求解.一般來說,采用D2Q4和D2Q5等計算量相對較小的離散速度模型足夠對標量場進行準確模擬.本文采用D2Q5離散速度對溫度場進行離散.

溫度分布函數的演化方程為

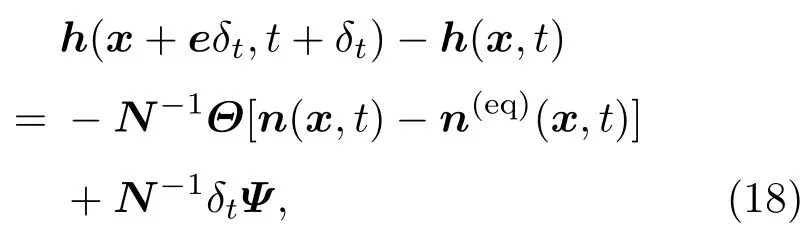
其中,h為溫度分布函數,n和n(eq)分別為h和h(eq)對應的矩空間分布函數,其中h(eq)為溫度平衡態分布函數,Ψ為源項,N轉換矩陣,Θ=diag(σ0,σ1,σ2,σ3,σ4)-1為松弛系數矩陣.

D2Q5離散速度{ei|i=0,1,···,4}為

轉換矩陣N為[25]

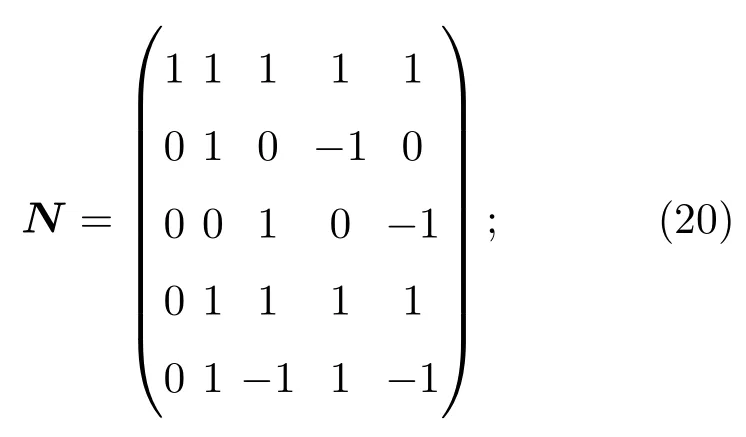
平衡態分布函數為

其中,?∈(0,1)為D2Q5離散速度模型中的參數.在本文模型中,?=1/2.

與標準笛卡爾坐標下的能量方程相比,柱坐標下的能量方程等號右邊多了一項這一項在本文模型中作為源項處理.為正確恢復宏觀柱坐標下的能量方程,源項Ψ采取如下形式：

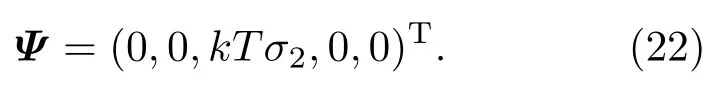
與求解速度場的MRT-LB模型類似,可通過轉換矩陣可將粒子溫度分布函數h(eq)投影到矩空間：

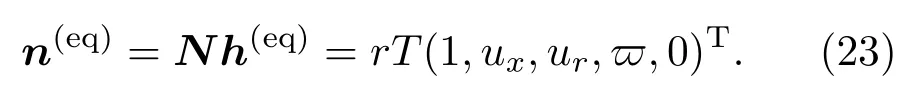
在實際應用中,求解溫度場的MRT-LB其演化過程與求解速度場的MRT-LB完全類似,即碰撞在矩空間進行,而遷移在速度空間進行.

宏觀量計算如下：

通過Chapman-Enskog多尺度展開,可以證明本文模型可以恢復對應的宏觀軸對稱能量方程(見附錄B).

3 數值模擬結果及討論

本節采用本文所提出的模型對幾種典型的軸對稱熱流動進行數值模擬以驗證模型的可行性和準確性,包括熱Womersley流動、豎直柱體空腔中的Rayleigh-Bénard流動和豎直環形柱體內的自然對流.計算中各松弛系數選取如下：s0=s1=s2=1.0,s3=s6=1.1,s7=s8=1.2,s4和s5根據(17)式計算.σ0=1.0,σ3=σ4=1.5,σ1和σ2根據(25)式計算.數值模擬中溫度場和速度場的MRT-LB模型通過Prandtl數和松弛系數進行耦合：

其中,Pr=ν/k為Prandtl數.固體邊界采用非平衡外推方法[26]進行處理.

3.1 熱Womersley流動

本節首先采用本文模型對熱Womersley流動問題進行模擬.恒定壁溫下的Womersley流動是工程中常見的一種流動現象.該流動是由周期性外力驅動的平直管道中的流動.周期性外力ax=Gcos(ωt),其中G為外力幅值,ω=2π/Tp為角頻率,Tp為周期.Womersley流動的特征數為Reynolds數和Womersley數,分別定義如下：

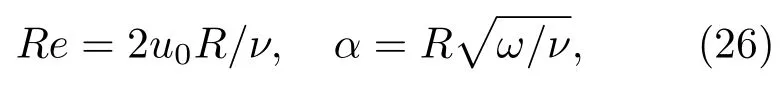
其中,R為管道半徑,ν為流體黏性,u0=GR2/4ν為特征速度.

Womersley流動的軸向速度的解析解為

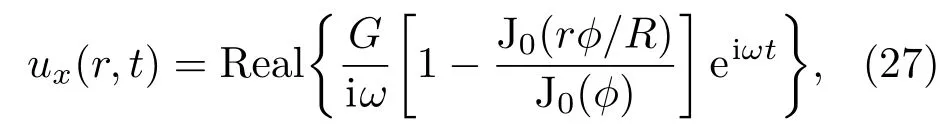
其中,i為虛數單位,φ=α(i-1)/2,J0為第一類零階Bessel函數.

溫度場的解析解為

計算中Re和α分別取為1200和8,Pr取為0.1,壁面溫度分別取為Tw=-1,1和3,流體初始溫度取為0.經過網格無關性驗證,計算網格取為Nx×Nr=82×42.流動在經過10個周期后達到相對的穩定狀態,此時軸向速度和溫度的分布與解析解應當相同.

圖1(a)為流動達到相對穩定狀態后一個周期內t=Tp/4,Tp/2,3Tp/4和Tp時刻軸向速度剖面圖和相應解析解的對比圖(為節省篇幅,由流動的軸對稱特征,圖1(a)只展示了關于軸心r=0對稱的1/2區域,后面的圖示類似處理).由圖1(a)可見,本文模型計算結果與解析解符合得很好.圖1(b)顯示了壁面溫度分別為Tw=-1,1和3,流場初始溫度取為0,流動達到相對穩定狀態后溫度場剖面圖與解析解對比情況,其中圓形、正方形和菱形符號分別對應Tw=-1,1和3時的數值解,實線為相應的解析解.可以看出溫度場的計算結果也與解析解完全相符.

圖1 Womersley流動軸向速度和溫度剖面圖 (a)不同時刻速度剖面圖;(b)不同壁面溫度時溫度剖面圖Fig.1.Axial velocity profiles of Womersley flow：(a)Velocity profiles at different times;(b)temperature profiles at different wall temperatures.

為驗證本文模型相對LBGK模型的數值穩定性,將兩模型進行了對比.首先采用現有的軸對稱LBGK模型[23]求解流場和溫度場.參數選取以及計算網格均與本節前面所述相同.對熱Womersley流動進行模擬,通過逐步減小黏性系數,發現在黏性系數ν=2.76×10-2時LBGK模型發散.而采用本文模型,當黏性系數ν=2.76×10-2時,模型依然穩定并給出準確結果(見圖2(a)).進一步,黏性系數取更小的值時,例如ν=2.0×10-2,本文模型依然穩定(見圖2(b)).數值實驗表明本文模型相對LBGK模型具有更好的數值穩定性.值得指出的是,雖然熱Womersley流動中速度場和溫度場是相互獨立的,但對于具體流動介質,流體黏性和熱擴散系數通過Pr數相互關聯(例如本例中Pr=ν/k=0.1),由于求解速度場的MRT-LB模型和求解溫度場的MRT-LB模型相互耦合,對于速度場數值穩定性的驗證也間接驗證了溫度場模型的數值穩定性.

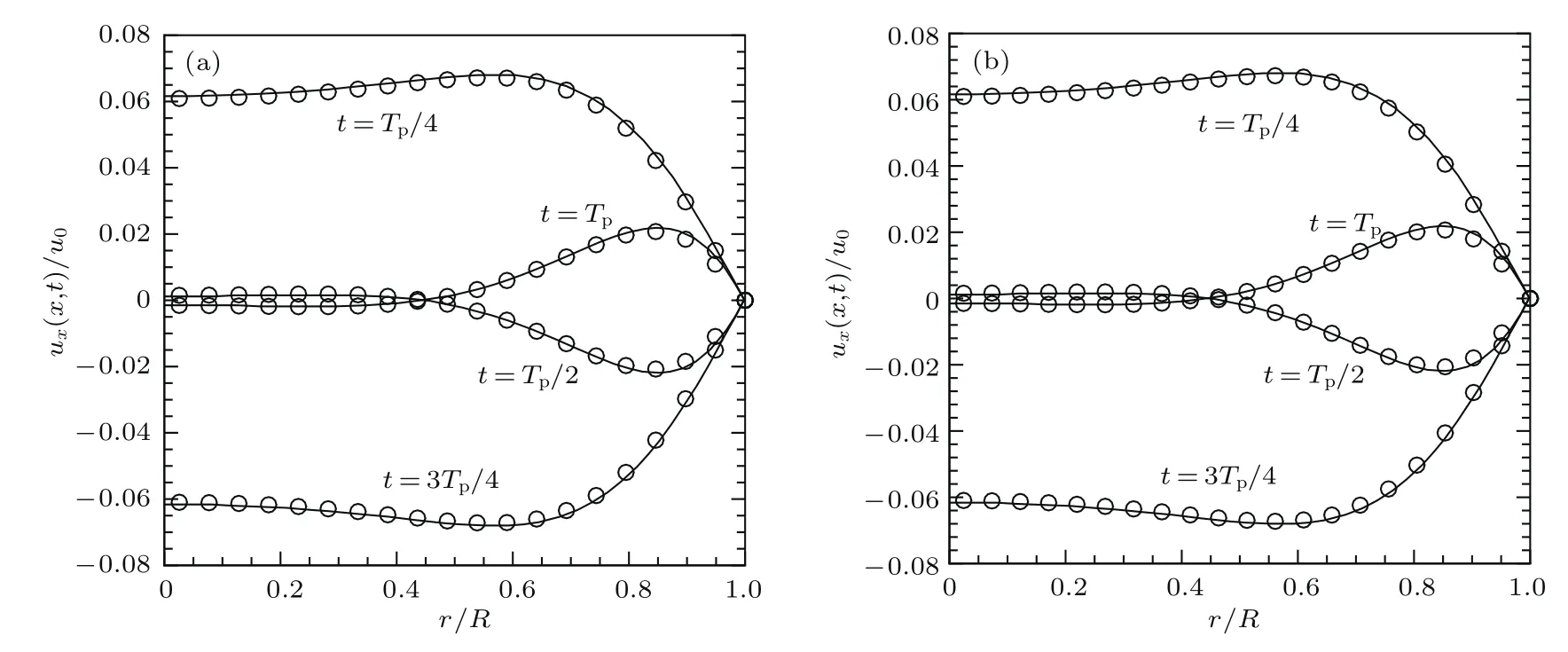
圖2 低黏性系數時本文模型所得Womersley流動軸向速度剖面圖 (a)ν=2.76×10-2;(b)ν=2.0×10-2Fig.2.Axial velocity profiles of Womersley flow at low viscosities：(a)ν=2.76×10-2;(b)ν=2.0×10-2.

3.2 豎直圓柱腔體中的Rayleigh-Bénard流動

Rayleigh-Bénard流動是常見的一種柱體內的自然對流現象,許多文獻對此進行過數值研究[18,27].自然對流的特征數為Ra數以及Pr數：

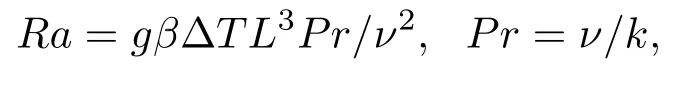
其中,g為重力加速度,β為熱膨脹系數,L為特征尺寸.本文引入Boussinesq假設,熱浮升力為ρa=-ρg(T-Tr),其中Tr為參考溫度.

在豎直圓柱腔體中的Rayleigh-Bénard自然對流問題中,充滿空氣的柱體腔體高為H,半徑為R,且H/R=1.柱體腔體上下面水平恒溫,溫度分別為Tc和Th,且Tc＜Th;其余壁面絕熱.計算中取Tc=0,Th=1,參考溫度Tr=(Ti+To)/2,Pr=0.7,Ra=5000,重力加速度g沿軸向負方向.對于自然對流,根據(17)式和(25)式以及Ra,Pr的定義,模型中未知的松弛系數可表示為

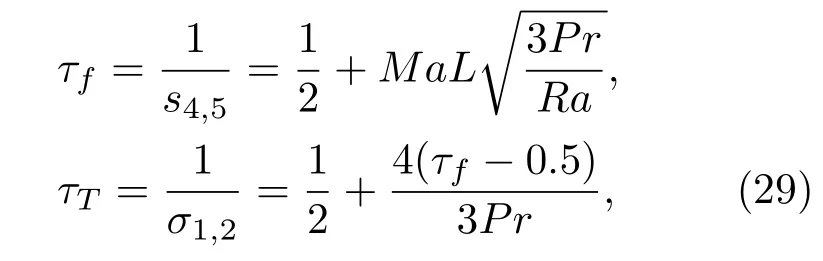
其中,L為特征尺寸,本例中取為H,Ma為Mach數,為滿足不可壓流動假設,本文取Ma=0.1.

計算中收斂標準定義為

首先取流場的初始溫度為0,經過網格無關性驗證,計算網格取為200×100.圖3(a)和圖3(b)分別顯示了采用本文模型計算的等溫線和流線圖(為節省篇幅,根據軸對稱特性只顯示了1/2區域).在流場溫度初始溫度為0時,腔體底部溫度高于周圍介質溫度,在重力作用下,空氣由腔體底部沿腔體中軸線向上運動,而在圓周壁面附近由上部向下部運動,形成穩定的渦.然后取流場的初始溫度為1,計算網格同樣取為200×100.圖4(a)和圖4(b)分別顯示了流動達到穩定狀態時的等溫線以及流線圖.可以看出,此時的流動特征正好與初始溫度為0時相反,即空氣沿腔體中軸線由上向下運動,而在圓周壁面附近由下向上運動.這些流動特征與文獻[18]以及文獻[27]完全相符.

為進一步對算法進行定量考核,表1給出了兩種情況下沿中軸線上的速度最大值,并與文獻[18]以及文獻[27]的計算結果進行了對比,其中無量綱速度定義為由表1可以看出采用本文模型計算所得結果與現有文獻符合得很好.

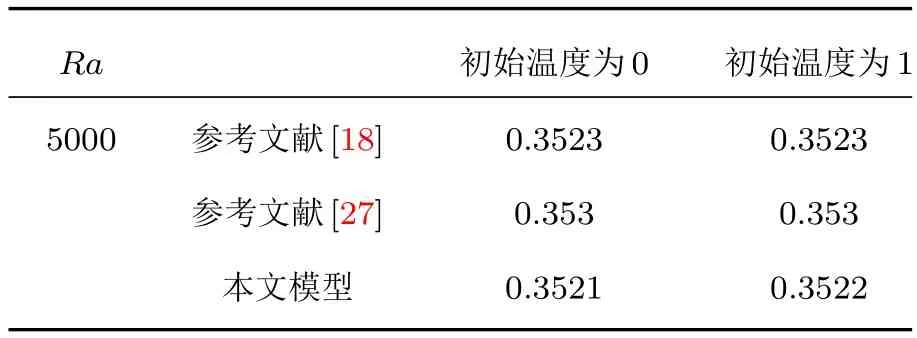
表1 本文模型獲得的中軸線上最大速度與已有研究結果的對比Table 1.Comparisons of the maximum velocity in the present study with those of the previous studies.

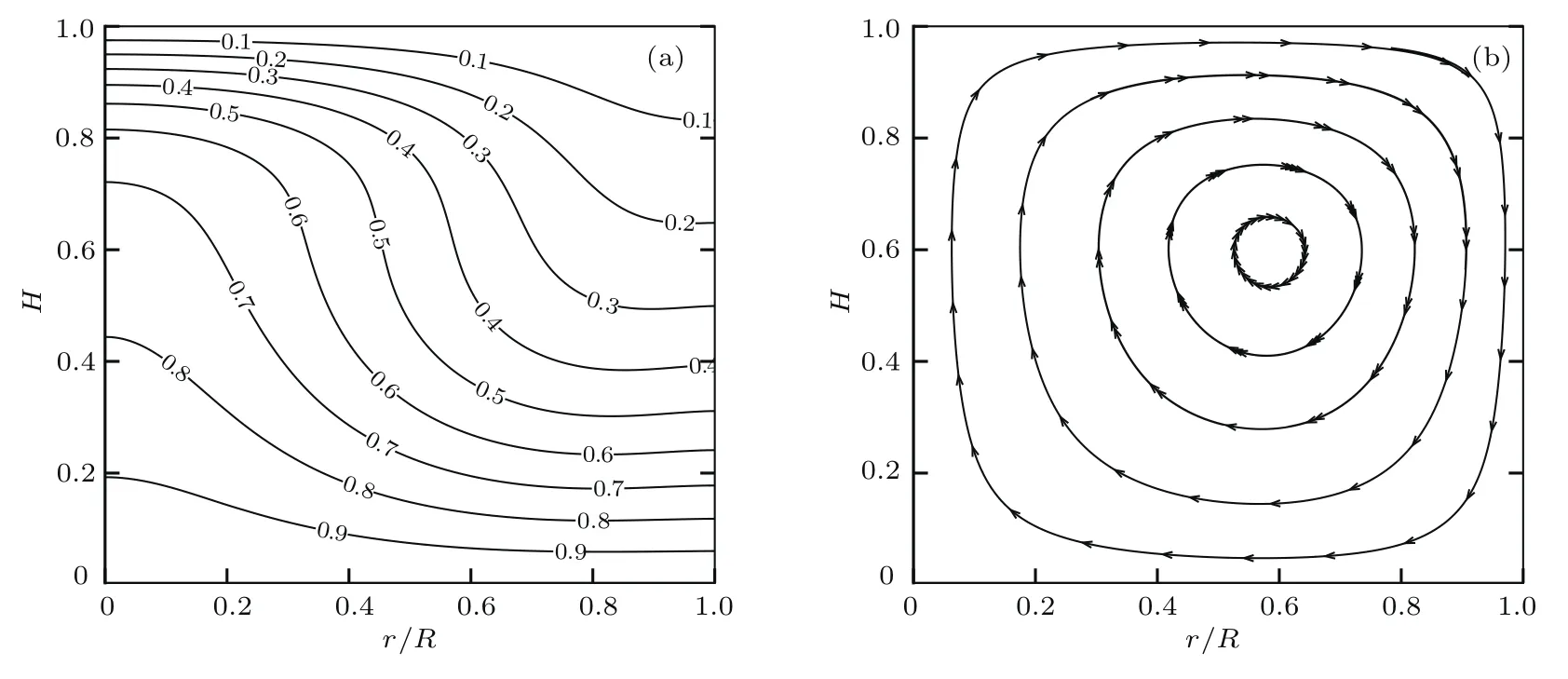
圖3 初始溫度為0時的等溫線和流線 (a)等溫線;(b)流線Fig.3.Isotherms and streamlines as the initial temperature is 0：(a)Isotherms;(b)streamlines.

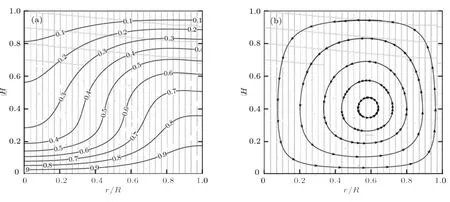
圖4 初始溫度為1時的等溫線和流線 (a)等溫線;(b)流線Fig.4.Isotherms and streamlines as the initial temperature is 1：(a)Isotherms;(b)streamlines.

3.3 豎直環形柱體的自然對流

本小節采用本文模型對豎直環形柱體內的自然對流進行數值模擬.環形柱體內的自然對流是一個廣泛研究的問題[17,28-30].流動區域由高度為H的內外兩個豎直同心圓柱之間的封閉區域構成,內外圓柱的半徑分別為ri和ro,其中ro=2ri,且H/ri=2.內外圓柱壁面溫度分別為Ti和To(Ti＞To),其他兩個水平邊界均為絕熱邊界.計算中分別取Ra=103,104和105,經過網格無關性驗證,對應的計算網格為100×200,200×400以及300×600.其他參數的選擇如下：To=0,Ti=1,參考溫度Tr=(Ti+To)/2,Pr=0.712,重力加速度g沿軸向負方向.豎直環形柱體自然對流的流動特征數、松弛系數的計算以及收斂標準與3.2節相同,不同的是特征尺寸L=ro-ri.

圖5給出了Ra=103,104和105時的等溫線圖.由圖5可見,當Ra較小時,腔體內以熱傳導為主,表現為等溫線在腔體內幾乎均勻分布且弱對流作用導致的等溫線變形不大.隨著Ra增大,對流開始起主要作用,導致腔體中央的等溫線扭曲程度變大.從圖6的流線也可以看出,隨著Ra增大,對流作用增強,流動呈現出更加復雜的特征.這些等溫線圖和流線圖均與文獻[17,28—30]符合得很好.

為與前人研究結果做定量比較,本文計算了內圓柱壁面的平均Nu數,其中Nu數定義為表2為采用本文模型獲得的內圓柱壁面的Nu數與已有研究結果的對比,可以看出符合良好,證明了本文模型的準確性.

圖5 不同Ra數時的等溫線圖 (a)Ra=103;(b)Ra=104;(c)Ra=105Fig.5.Isotherms at differentRanumbers：(a)Ra=103;(b)Ra=104;(c)Ra=105.

圖6 不同Ra數時的流線圖 (a)Ra=103;(b)Ra=104;(c)Ra=105Fig.6.Streamlines at differentRanumbers：(a)Ra=103;(b)Ra=104;(c)Ra=105.

表2 本文模型獲得的內圓柱壁面的Nu數與已有研究結果的對比Table 2.Comparisons of the average Nusselt numbers in the present study with those of the previous studies.

由于本文模型采用了非正交轉換矩陣,前文提到,相對于現有的正交轉換矩陣,非正交轉換矩陣具有更多的零元素,理論上可以獲得更高的數值計算效率.本節采用豎直柱體環中的自然對流算例對本文模型和現有的基于正交矩陣的軸對稱MRTLB模型[22](其中,溫度場的求解采用文獻[18]模型的MRT格式)進行對比.計算中Ra=103,104和105的網格尺度分別為100×200,200×400以及300×600.計算在同一臺3.40 GHz主頻的計算機上進行.表3列出了現有模型和本文模型計算耗時的對比.由表3可見,對于網格數較少的情況,本文模型計算效率提高了3.5%.然而隨著計算網格量的增大,本文模型效率提高幅度變大,對于300×600的計算網格,相對現有模型,本文模型效率提高了4.6%.可以預期,對于對計算網格量要求更高的復雜流動,本文模型將獲得更高的效率,特別是對于計算周期長的數值模擬,計算時間的縮短將特別明顯.

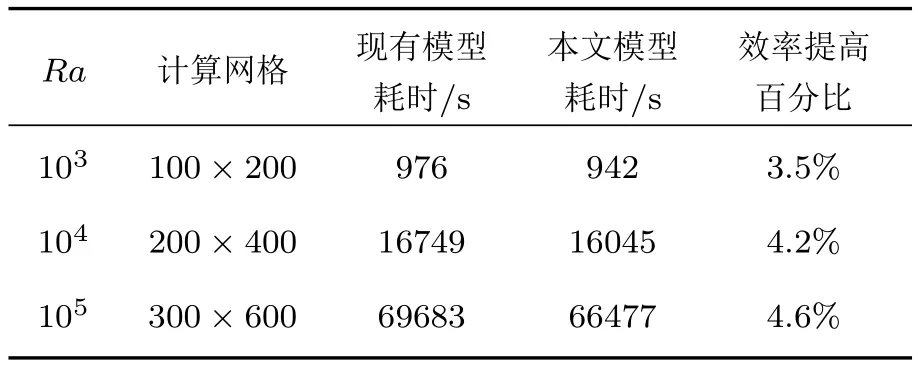
表3 本文模型與現有模型的效率對比Table 3.Comparisons of the computation efficiency of the present model with that of the existing model.

4 結 論

本文提出了一種軸對稱熱流動的MRT-LB模型,模型的速度場采用D2Q9離散速度求解,溫度場采用D2Q5離散速度求解.本文模型的轉換矩陣采用非正交轉換矩陣,相比現有MRT-LB模型的正交矩陣具有更多的零元素,因此本文模型相比現有的軸對稱MRT-LB模型具有更高的計算效率.Chapman-Enskog多尺度分析表明,本文模型可恢復對應的宏觀柱坐標下的連續方程、動量方程以及能量方程.通過對熱Womersley流動、豎直圓柱腔體中的Rayleigh-Bénard對流和豎直環形柱體內的自然對流進行數值模擬,證明了本文模型的可行性和準確性.低黏性系數條件下的數值實驗表明,相對現有軸對稱LBGK模型,本文模型具有更好的數值穩定性.且與現有的軸對稱MRT-LB模型相比,本文模型具有更高的計算效率.

附錄A速度場MRT-LB模型的Chapman-Enskog多尺度分析

為證明本文模型可以正確恢復宏觀的柱坐標下的Naiver-Stokes方程,采用Chapman-Enskog多尺度分析方法對求解速度場的MRT-LB模型進行分析.首先對以下變量進行如下形式的多尺度展開:

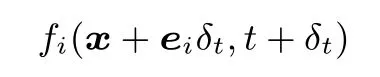
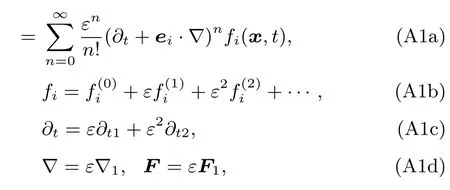
其中,ε為與Knudsen數同量級的展開系數,對于宏觀尺度,0＜ε?1.

將(A1a)—(A1d)式代入方程(5)中,可得以下不同空間(時間)尺度上的方程:

由(A2b)式可以得到t1時間尺度上的方程:

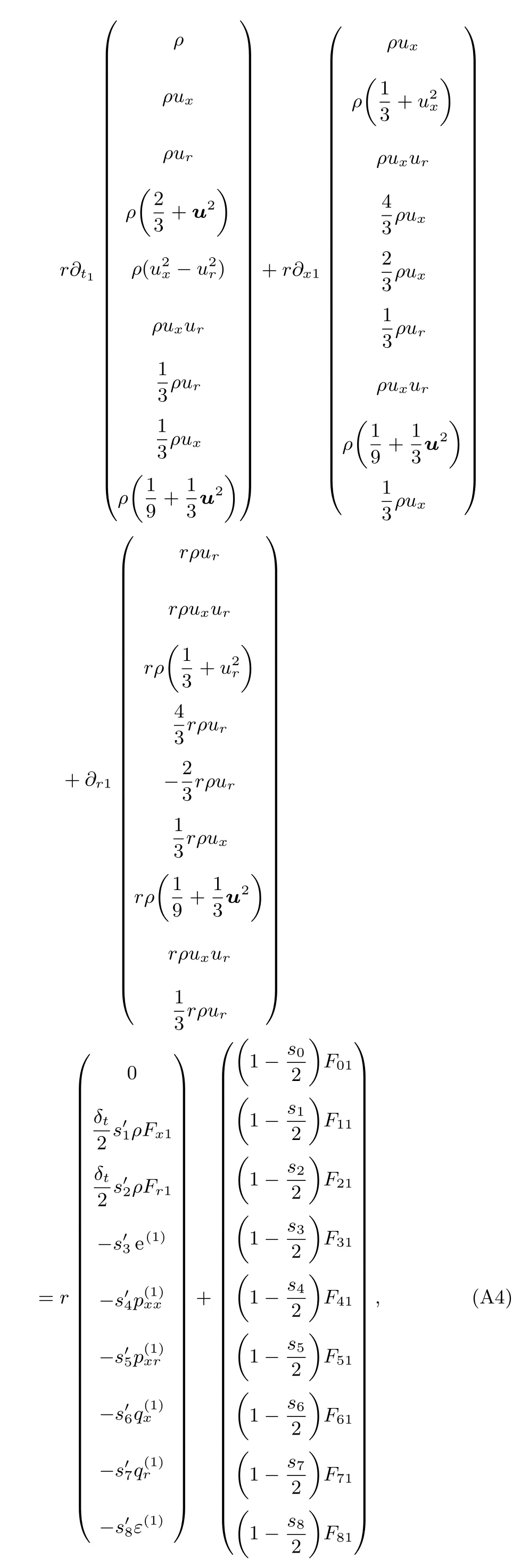
由(A2c)式可以得到t2時間尺度上的方程:

根據(A4)式第一、二和三行方程,忽略其中O(Ma3)的高階項,可得

將(A6a)—(A6d)式代入(A4)式第四至第六行方程,可求得:

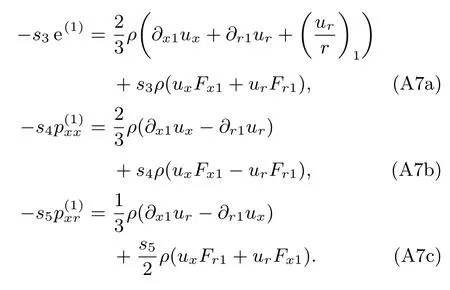
將(A7a)—(A7c)式代入(A5b)式和(A5c)式,可得t2時間尺度上的方程:

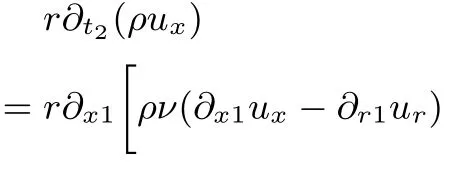
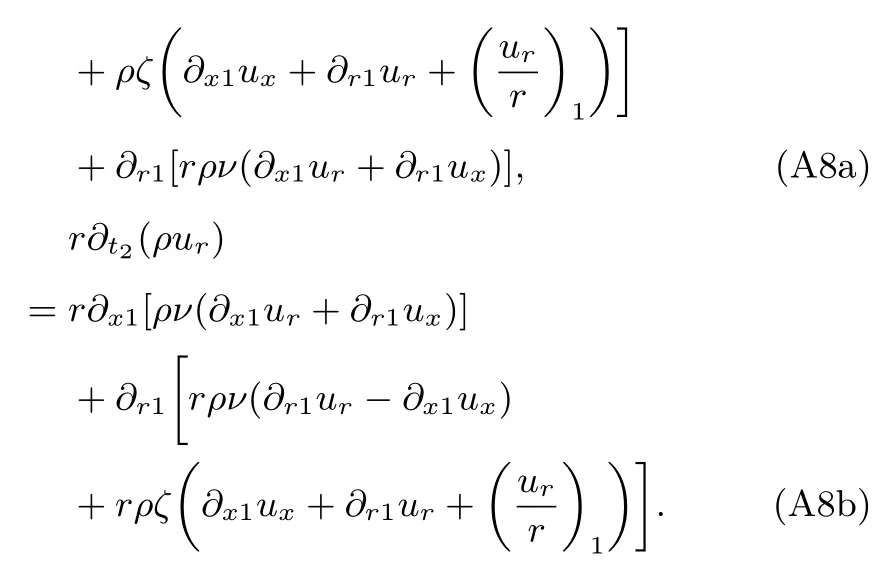
聯合t1時間尺度上的方程(A4)與t2時間尺度上的方程(A8a)和(A8b),可得宏觀控制方程(1)—(3),其中動力黏性系數以及體積黏性系數分別定義為

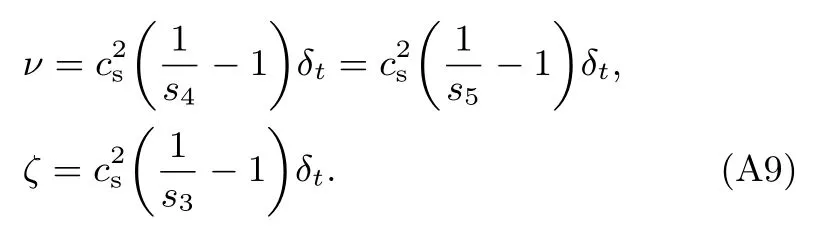
附錄B溫度場MRT-LB模型的Chapman-Enskog多尺度分析

同樣對溫度分布函數進行與(A1a)—(A1d)式類似的多尺度展開,并將展開結果代入方程(18)中,可得以下不同空間(時間)尺度上的方程:

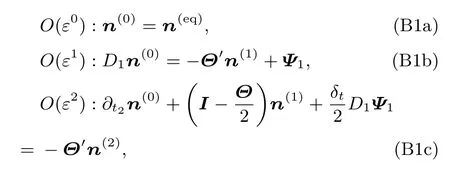
其中,D1=?t1I+Eα?α1,Eα=N(eiαI)N-1,Θ′=

矩陣E=(Ex,Er)可顯式地表達為[25]

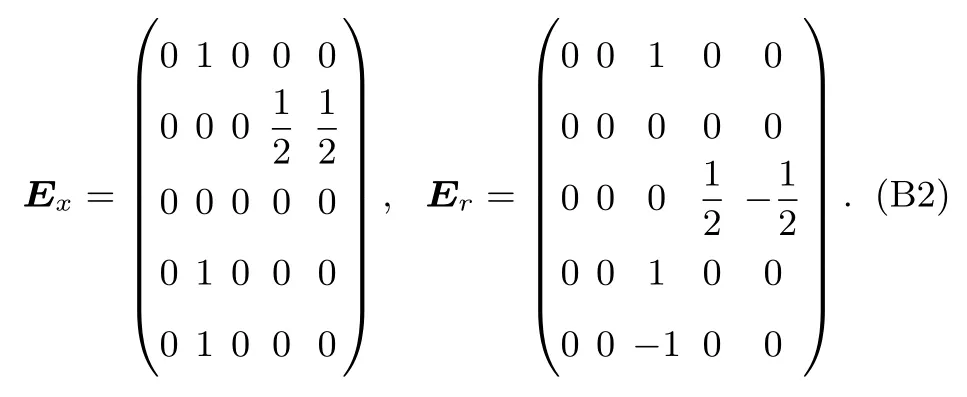
由(B1b)式可以得到t1時間尺度上的方程:

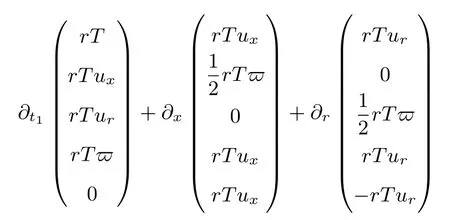
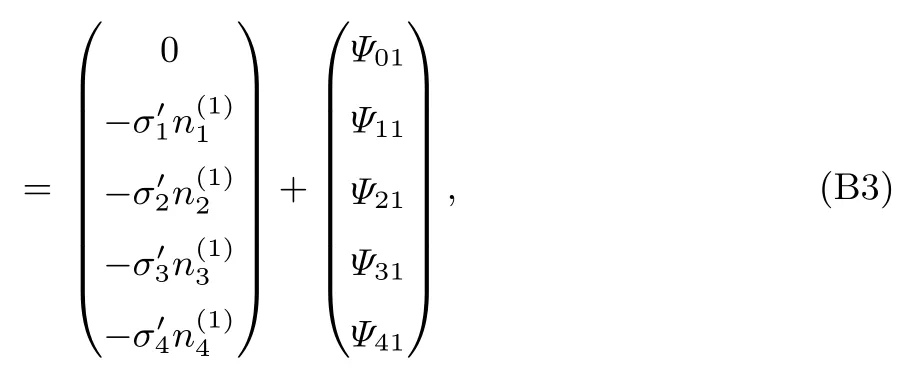
其中,Ψ01—Ψ41分別表示t1時間尺度上的源項Ψ1=(0,0,kTσ2,0,0)T的對應分量.

由(B1c)式可得t2時間尺度上的方程:

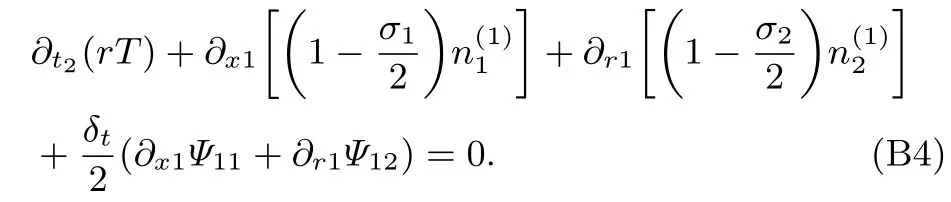
由(B3)的第二行和第三行可得

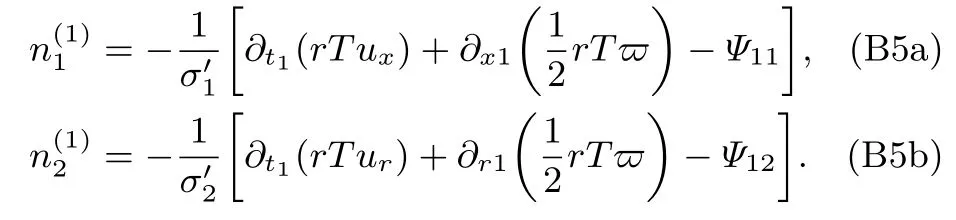
對于不可壓流動,(B5a)和(B5b)式的時間相關項可以忽略[25],所以(B5a)和(B5b)式可進一步簡化為

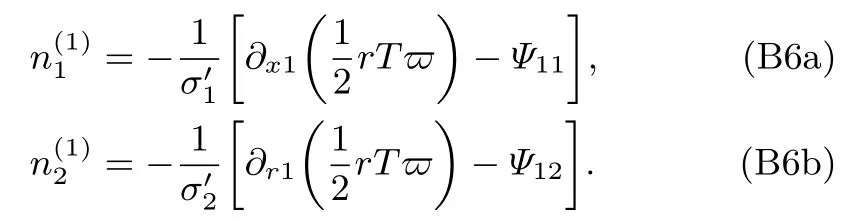
將(B6a)和(B6b)式代入(B4)式,并考慮到(Ψ11,Ψ12)T=(0,kTσ2)T,可得:

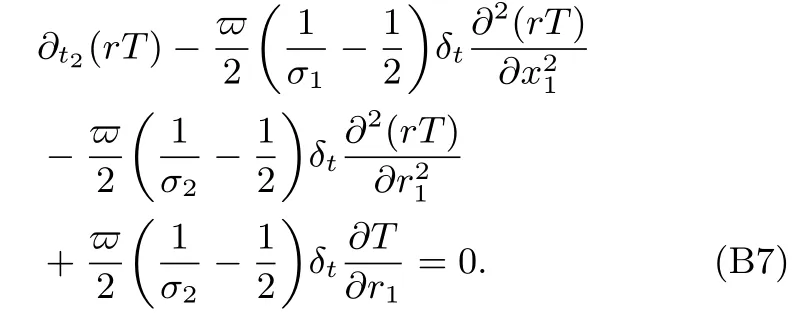
結合t1時間尺度上的方程(B3)的第一行方程與t2時間尺度上的方程(B7),并考慮到柱坐標下的不可壓流動的連續方程,可得軸對稱溫度場的宏觀控制方程(4),其中熱擴散系數定義為

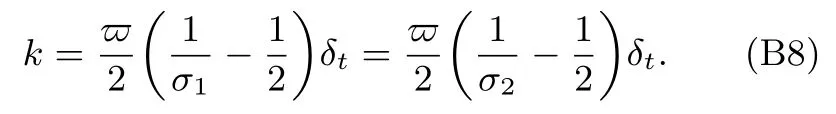
[1]Vynnycky M,Maeno N 2012Int.J.Heat Mass Transfer55 7297

[2]Grosan T,Pop I 2011Int.J.Heat Mass Transfer54 3139

[3]Huang H,Hong N,Liang H,Shi B C,Chai Z H 2016Acta Phys.Sin.65 084702(in Chinese)[黃虎,洪寧,梁宏,施保昌,柴振華2016物理學報65 084702]

[4]Aidun C K,Clausen J R 2009Annu.Rev.Fluid Mech.42 439

[5]Li Q,Luo K H,Kang Q J,He Y L,Chen Q,Liu Q 2015Prog.Energy Combust.Sci.52 62

[6]Lallemand P,Luo L S 2000Phys.Rev.E61 6546

[7]d’Humières D,Ginzburg I,Krafczyk M,Lallemand P,Luo L S 2002Philos.Trans.R.Soc.London A360 437

[8]Halliady I,Hammond L A,Care C M,Good K,Stevens A 2001Phys.Rev.E64 011208

[9]Lee T S,Huang H,Shu C 2006Int.J.Mod.Phys.C17 645

[10]Reis T,Phillips T N 2007Phys.Rev.E75 056703

[11]Reis T,Phillips T N 2008Phys.Rev.E2008 77 026703

[12]Guo Z L,Han H F,Shi B C,Zheng C G 2009Phys.Rev.E79 046708

[13]Li Q,He Y L,Tang G H,Tao W Q 2010Phys.Rev.E81 056707

[14]Zhou J G 2011Phys.Rev.E84 036704

[15]Peng Y,Shu C,Chew Y T,Qiu J 2003J.Comput.Phys.186 295

[16]Huang H,Lee T S,Shu C 2007Int.J.Numer.Methods Fluids53 1707

[17]Li Q,He Y L,Tang G H,Tao W Q 2009Phys.Rev.E80 037702

[18]Zheng L,Shi B C,Guo Z L,Zheng C G 2010Comput.Fluids39 945

[19]Meng X,Guo Z L 2015Phys.Rev.E92 043305

[20]Liu Q,He Y L 2015Physica A429 215

[21]Li Q,He Y L,Tang G H,Tao W Q 2011Microfluid.Nanofluid.10 607

[22]Wang L,Guo Z L,Zheng C G 2010Comput.Fluids39 1542

[23]Premnath K N,Banerjee S 2009Phys.Rev.E80 036702

[24]Geier M,Sch?nherr M,Pasquali A,Krafczyk M 2015Comput.Math.Appl.70 507

[25]Liu Q,He Y L,Li D,Li Q 2016Int.J.Heat Mass Transfer102 1334

[26]Guo Z L,Shi B C,Zheng C G 2002Chin.Phys.B11 366

[27]Lemembre A,Petit J P 1998Int.J.Heat Mass Transfer41 2437

[28]Li L K,Mei R W,Klausner J F 2013Int.J.Heat Mass Transfer67 338

[29]Kumar R,Kalam M A 1991Int.J.Heat Mass Transfer34 513

[30]Venkatachalappa M,Sankar M,Natarajan A A 2001Acta Mech.147 173

PACS:47.11.—j,02.60.Cb DOI:10.7498/aps.66.044701

Non-orthogonal multiple-relaxation-time lattice Boltzmann method for axisymmetric thermal flows?

Wang Zuo Zhang Jia-Zhong?Wang Heng

(School of Energy and Power Engineering,Xi’an Jiaotong University,Xi’an 710049,China)

3 September 2016;revised manuscript

22 November 2016)

Axisymmetric thermal flows in cylindrical systems are widely encountered in engineering practices.Typically,axisymmetric thermal flows belong in three-dimensional(3D)problems.However,taking advantage of the axisymmetric condition,the 3D axisymmetric flows can be reduced to quasi two-dimensional(2D)problems in the meridian plane,which significantly reduces the computational requirements and avoids treating the curved boundary.In recent years,various 2D lattice Boltzmann(LB)models,including single relaxation time LB(SRT-LB,or LBGK)and multiple relaxation time LB(MRT-LB)models,for axisymmetric thermal flows have been proposed.In the LB community,it is well accepted that the MRT-LB is superior to the LBGK in terms of numerical stability.The existing MRT-LB model for axisymmetric thermal flows are developed based on orthogonal basis vectors obtained from the combination of the lattice velocity components,i.e.,the transform matrix in the existing MRT-LB is an orthogonal one.Unlike the existing MRT-LB model,in this paper,a non-orthogonal multiple-relaxation-time lattice Boltzmann(MRT-LB)method of simulating axisymmetric thermal flows is proposed.In the proposed MRT-LB method,the velocity field is solved by a D2Q9 discrete velocity set while the temperature by a D2Q5 discrete velocity set.The main advantage of the present MRT-LB model is that the transform matrix of the model is a non-orthogonal one,which is comprised of some proper non-orthogonal basis vectors obtained from the combination of the lattice velocity components.The non-orthogonal transform matrix of the present MRT-LB model contains more zero elements than the classical orthogonal transform matrix,and thus the present MRT-LB model is expected to be more efficient than the existing orthogonal-based MRT-LB model.The equilibrium velocity and temperature moments of the present MRT-LB model are expressed by mapping the equilibrium distribution functions onto their moment spaces through using the non-orthogonal transformation matrix.Also the vectors in the forcing term are modified according to the matrix mapping.Through the Chapman-Enskog analysis,it is demonstrated that the macroscopic governing equations in the cylindrical coordinate can be recovered from the present MRT-LB model.Then several numerical tests,including thermal Womersley flow,Rayleigh-Bénard convection in a vertical cylinder and natural convection in a vertical annulus,are conducted to validate the present model.It is found that the present numerical results are in good agreement with the analytical solutions and/or other numerical results reported in the literature.Numerical stability is also tested,and the results suggest that the present MRT model shows better numerical stability than its LBGK counterpart.Moreover,the numerical results also indicate that the present MRT-LB model is more computationally efficient than the existing MRT-LB model for axisymmetric thermal flow.These findings indicate that the present MRT-LB model can serve as a powerful method of computing the axisymmetric thermal flows.

axisymmetric thermal flow,lattice Boltzmann method

:47.11.—j,02.60.Cb

10.7498/aps.66.044701

?國家重點基礎研究發展計劃(批準號：2012CB026002)和國家重點科技支撐項目(批準號：2013BAF01B02)資助的課題.

?通信作者.E-mail：jzzhang@mail.xjtu.edu.cn

*Project supported by the National Fundamental Research Program of China(Grant No.2012CB026002)and the National Key Technology Research and Development Program of China(Grant No.2013BAF01B02).

?Corresponding author.E-mail：jzzhang@mail.xjtu.edu.cn