滲透數字思想提升學科素養

陳曉娟

摘要：本文以蘇教版《數學》三年級下冊"認識小數"為例，探討在課堂教學中發展學生數學學科素養的途徑：借助直觀模型，發展抽象思想；通過多元表征，發展數形結合思想；引導系統勾連，發展推理思想。

關鍵詞：抽象思想；數形結合思想；推理思想；數學學科素養

中圖分類號：G623.2 文獻標識碼：B 文章編號：1672-1578（2017）06-0180-01

數學思想融入小學數學課程，經歷了從內容滲透到成為課程目標的過程。下面以"小數的初步認識"教學為例，談談如何在課堂教學中滲透數學思想，提升學生的數學學科素養，從而讓學科內容更有教育價值。

1.直觀模型

發展抽象思想抽象，是指舍棄事物個別的、非本質的屬性，抽取出本質屬性的過程和方法。學生建構數學概念的過程，不是教師簡單"告知"，而需要教師"適時后退"，真正把學習的主動權交給學生，讓學生基于經驗，自主探索數學概念的本質意義。從學生的前測來看，他們對具體情境中小數的含義有一定認識，特別是價格中的小數。

筆者跟學生約定用一個長方形表示1元，讓學生自主表示0.3元。學生依據生活經驗，知道0.3元是3角，1元等于10角，3角不滿1元，通過交流、分析得到把l元平均分成10份，這樣的3份就是3角，就是十分之三元，也就是0.3元。除了用一個長方形表示1元，學生還想到可以用圓、線段等圖形表示1元，圖形放大或縮小都不影響所表示的小數。一個長方形除了可以表示1元，還可以表示1米、1千克、1升等。如果1個長方形不表示具體的量，只表示"1"，那么為了在這個長方形里表示出零點幾的小數，學生可以聯系分數的意義，觀察、比較小數和分數的關系，水到渠成地抽象出一位小數的意義。

2.多元表征，發展數形結合思想

數和形是數學研究的兩個基本對象，"數"構成了數學的抽象化符號語言，"形"構成了數學的直觀化圖形語言。我國數學家華羅庚對"數"與"形"之間的密切聯系有過一段精彩的描述："數與形本是相依，焉能分作兩邊飛，數缺形少直覺，形少數難入微，數形結合百般好，隔裂分家萬事休，切莫忘，幾何代數統一體，永遠聯系切莫分離。"寥寥數語，把"數形結合"之妙說得淋漓盡致。用數形結合的方式，可以將小數具體化、形象化，便于學生理解。

筆者在課前做過讓學生畫圖表示0.3元的前測。其中，有13名學生能畫線段圖或長方形圖等正確表示0.3元。如：

有15名學生想到了把1元分成10份，但沒有平均分，也未聯系分數來實現平均分，對一位小數意義的理解達不到抽象水平。如：

還有12名學生不清楚0.3元和1元之間的關系，但他們知道0.3元里有3個0.1元，0.3元就是3角，他們對小數意義的理解處于混沌狀態。如：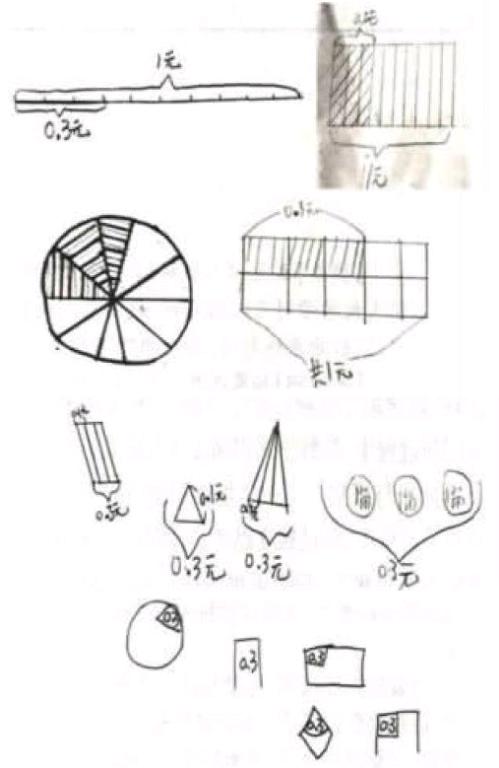

最困難的1名學生知道0.3元比1元小，但不明白它們之間到底是什么關系，對小數的意義建構處于游離狀態：

筆者先讓學生用一個長方形表示1元，學生嘗試借助1元的長方形圖表示0.3元并思考0.3元的原生態多元表征。一句"你還會用其他的圖來表示0.3元嗎"的追問，為學生打開了思維之門，不同層次的學生利用不同素材（線段、長方形、正方形等）再次進行豐富的表征，給接下來"這些圖形的形狀不同，為什么都可以表示出相應的小數"這一追問提供了豐富的資源。學生在經歷歸納過程的同時，還有以下收獲：線段圖上的表征與后續在數軸上表示小數可以進行對接；在數軸上表示整數和小數，利于學生發現整數與小數、小數與小數之間的關系并滲透區間的概念，為以后學習"小數的大小比較"做好鋪墊。

3.系統勾連。發展推理思想

"整數一十分之幾的分數一小數"是"小數"知識的發展脈絡。建立小數與整數的聯系以及小數與分母是10的分數的對應是理解小數意義的核心。思維的能動性可以通過推理幫助人類突破感官、經驗、常識的局限。學生通過0.1表示十分之一、0.2表示十分之二……這樣的歸納推理，抽象出一位小數的意義，認識到小數概念的體系不僅指某個具體單獨的數，也包括數與數之間的聯系。

筆者先通過數軸呈現一系列整數，再讓學生在兩個整數之間推想相關的小數，最后在小數之間推想更小的小數，以此引導學生在-個系統較強的層面上認識小數，理解小數，建構整數、分數與小數之間的聯系。

課堂具有不可重復、智慧生成的特點，其具體內容總會隱含一些獨特的突破口來承載我們的教學目標。因此，教師需要找準突破口，把必要性、可能性落實到具體的教學中。

參考文獻：

[1] 中華人民共和國教育部.義務教育數學課程標準（2011年版）[s].北京：北京師范大學出版社，2012.

[2] 曹培英.從學科核心素養與學科育人價值看數學基本思想[J].課程·教材·教法，2015（9）.