基于精細積分法的軸承-拉桿轉子系統非線性動力學分析
黑棣,鄭美茹
(陜西鐵路工程職業技術學院 機電工程系,陜西 渭南 714000)
軸承-轉子系統作為旋轉機械的核心部件,廣泛應用于航天、電力、工程等領域。許多學者針對軸承-轉子系統的相關問題進行了研究。文獻[1-2]研究了表面織構對滑動軸承性能的影響。文獻[3]求解了Reynolds方程,并且得到油膜壓力分布曲線,分析了各種參數對油膜力的影響。文獻[4]利用變分原理和分離變量法求得了油膜力的近似解析解。
以上研究都是為了能夠更準確地進行軸承-轉子系統的動力學分析。因為系統的穩定性直接決定旋轉機械運行的穩定性,因此,軸承-轉子系統動力學分析計算十分關鍵,最常用的軸承-轉子系統動力學計算方法有Runge-Kutta法[5-6]、Wilson-θ法[7-8]、Newmark法[9-10]等,但均對計算步長的依賴較大。
精細積分法對步長的依賴較小,而且能保證較高的精度。文獻[11]基于2N類算法提出了精細積分法。文獻[12]將Wilson-θ法和精細積分法結合分析了結構地震時程反應。文獻[13]給出了單步4階精度的精細積分法,該方法精度高,計算量小。文獻[14]采用改進的精細積分法計算了轉子系統的非線性動力學行為。文獻[15]將數據庫方法與精細時程積分法相結合,研究了可傾瓦軸承-轉子系統的動力學響應。
現基于改進的精細積分法,將其與傳統的Wilson-θ法、Newmark法進行比較,求解轉子系統的非線性動力學響應,研究步長對轉子系統的非線性動力學行為的影響。
1 轉子系統運動方程
拉桿轉子系統模型如圖1所示。圖中:O1和O2為2個圓盤的中心;mO1,mO2分別為兩圓盤的質量;eO1,eO2分別為兩圓盤的偏心量;l為轉軸的總長;a和b為兩轉軸的長度;AO1=a1,BO1=b1,AO2=a2,BO2=b2;ma,mb分別為 AO,BO的集中質量;fx和 fy分別為軸承處x,y方向上的油膜力。
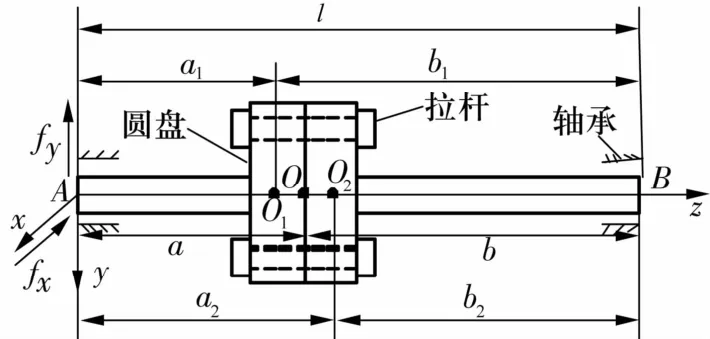
圖1 軸承-拉桿轉子系統示意圖Fig.1 Sketch of bearing-rod fastening rotor system



式中:M為質量矩陣;G為陀螺矩陣;K為剛度矩陣;F為非線性油膜力向量;FAx,FAy-分別為軸承A處轉子x,y方向的無量綱非線性油膜力;FBx,FBy-分別為軸承B處轉子x,y方向的無量綱非線性油膜力;Q為外激勵列向量;W為重力列向量;FR為圓盤間的非線性回復力;KR為量綱一的非線性回復剛度;Kb為拉桿量綱一的彎曲剛度。q為位移列向量;XA,YA,XO1,YO1,XO2,YO2,XB,YB分別為轉子在軸承A端、圓盤O1處、圓盤O2處、軸承B端 x和 y方向的位移;θx1,θy1,θx2,θy2分別為圓盤1,2繞x和y軸的擺角;Jd1,Jd2分別為圓盤1,2的極轉動慣量;Jz1,Jz2分別為圓盤1,2的赤道轉動慣量;k11,k22分別為AO軸段x,y方向的彎曲剛度;k′11,k′22分別為 OB軸段 x,y方向的彎曲剛度;k33,k44,k′33,k′44分別為由于圓盤 1,2繞 x和 y軸擺動而引起的軸段剛度;k14,k23為AO軸段的交叉剛度;k′14,k′23為 OB軸段的交叉剛度,由于轉子的對稱性,有 k11=k22=k′11=k′22,k33=k44=k′33=k′44,k14=k23,k′14=k′[16]23;kR為非線性回復剛度;kb為拉桿的彎曲剛度。
2 改進的精細積分法
2.1 算法介紹
運用精細積分法求解轉子系統的動力學響應,將(1)式化為


2.2 算法驗證
為了驗證該算法的有效性,針對以下算例,將其與Newmark法、Wilson-θ法進行比較。

分別采用3種算法進行計算,計算結果與精確解見表1。
由表1可以看出,文中方法的計算結果比Newmark法、Wilson-θ法更接近精確解。
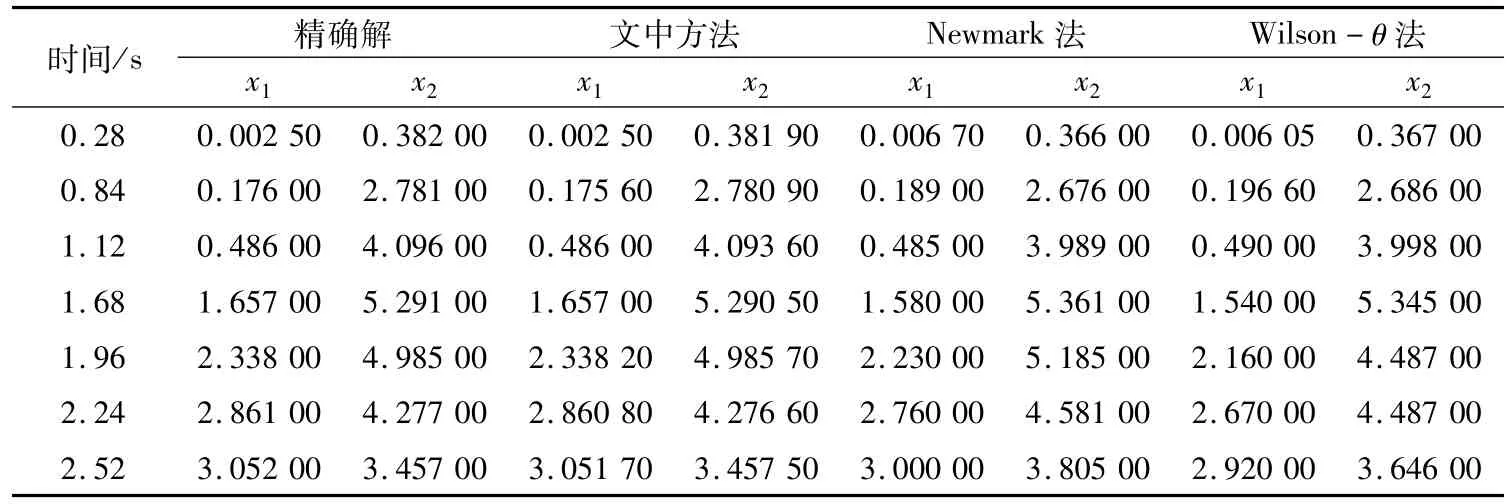
表1 3種方法計算結果Tab.1 Calculation results of three kinds of methods
3 數值算例
軸承-對稱拉桿轉子系統參數如下。軸承為360°徑向滑動軸承,軸承寬度和直徑之比D/d=1,μ=0.022 Pa·s,c=0.000 49 m。轉軸參數:r=0.14 m,l=3.3m,a=1.6m,b=1.6m,a1=1.4 m,b1=1.8 m,a2=1.8m,b2=1.4m,mA=mB=768.458 7 kg。圓盤參數:h=0.4 m,R=0.3 m,eO1=eO2=0.01c,mO1=mO2=690.044 5 kg,Jz1=Jz2=31.052 kg·m2,Jd1=Jd2=15.526 kg·m2。2m=mA+mB+mO1+mO2,m=1 458.5 kg。轉軸剛度:k11=k22=k′11=k′22=9.992 5×107N/m,k14=k23= -3.758 4×107N/m,k′14=k′23=3.758 4×106N/m,k33=k44=k′33=k′44=2.367 8×108N/m,kb=kR=2 k11。
以轉子的量綱一轉速為控制參數分析轉子的非線性動力學行為,其計算步長為 h=2π/200。當量綱一轉速的變化范圍為0.9~1.05時,轉子軸承處和圓盤處y方向位移隨轉速的運動分岔圖如圖2所示。
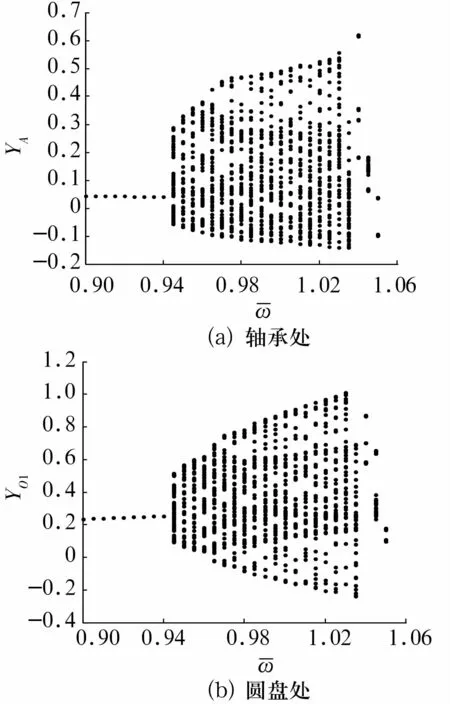
圖2 轉子軸承和圓盤處y方向位移隨轉速的運動分岔圖Fig.2 Bifurcation diagram of y versus at bearing station and disk stations
由圖2可以看出,轉速較低時,轉子系統的運動為周期運動,隨著轉速的升高,轉子系統將發生分岔行為。
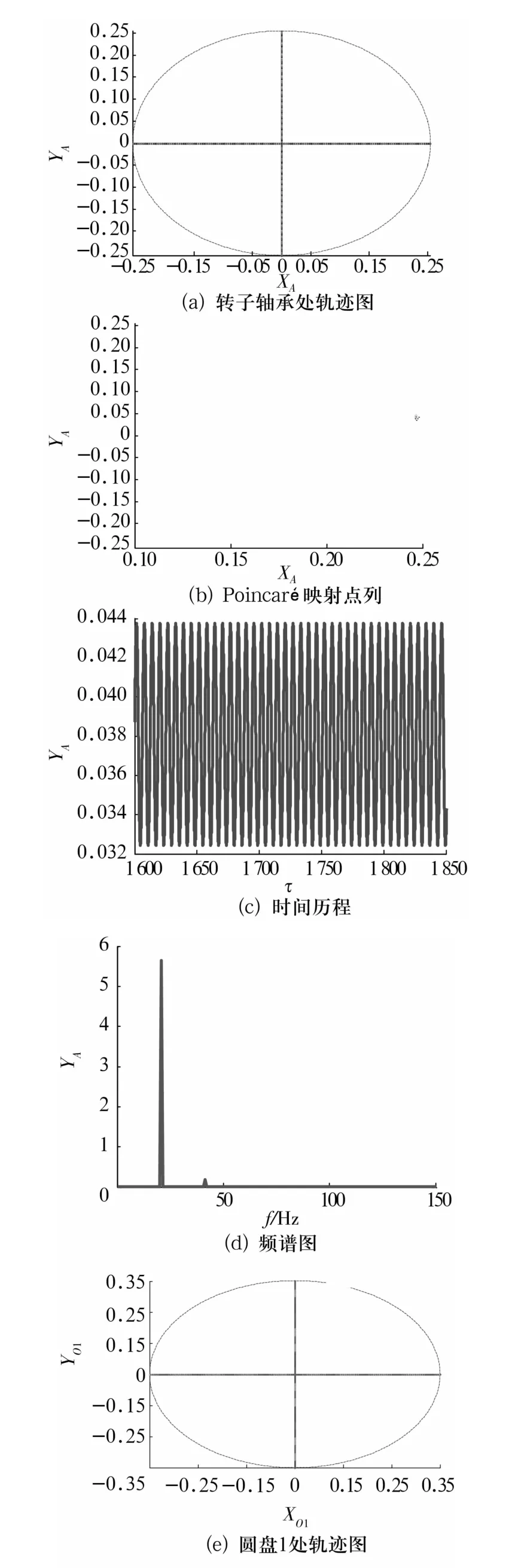
圖3 =0.92時轉子軸承處的軌跡圖、Poincaré映射圖、時間歷程、頻譜圖和圓盤1處的軌跡圖Fig.3 The orbit,Poincaré map,time series,spectrum of the rotor at bearing station and the orbit of disk 1 for=0.92
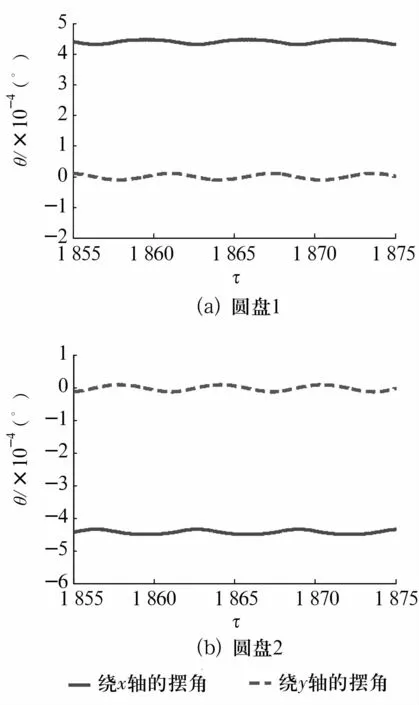
圖4 =0.92時圓盤分別繞x,y軸的擺角Fig.4 The swing angle of disks around the x and y axis for=0.92
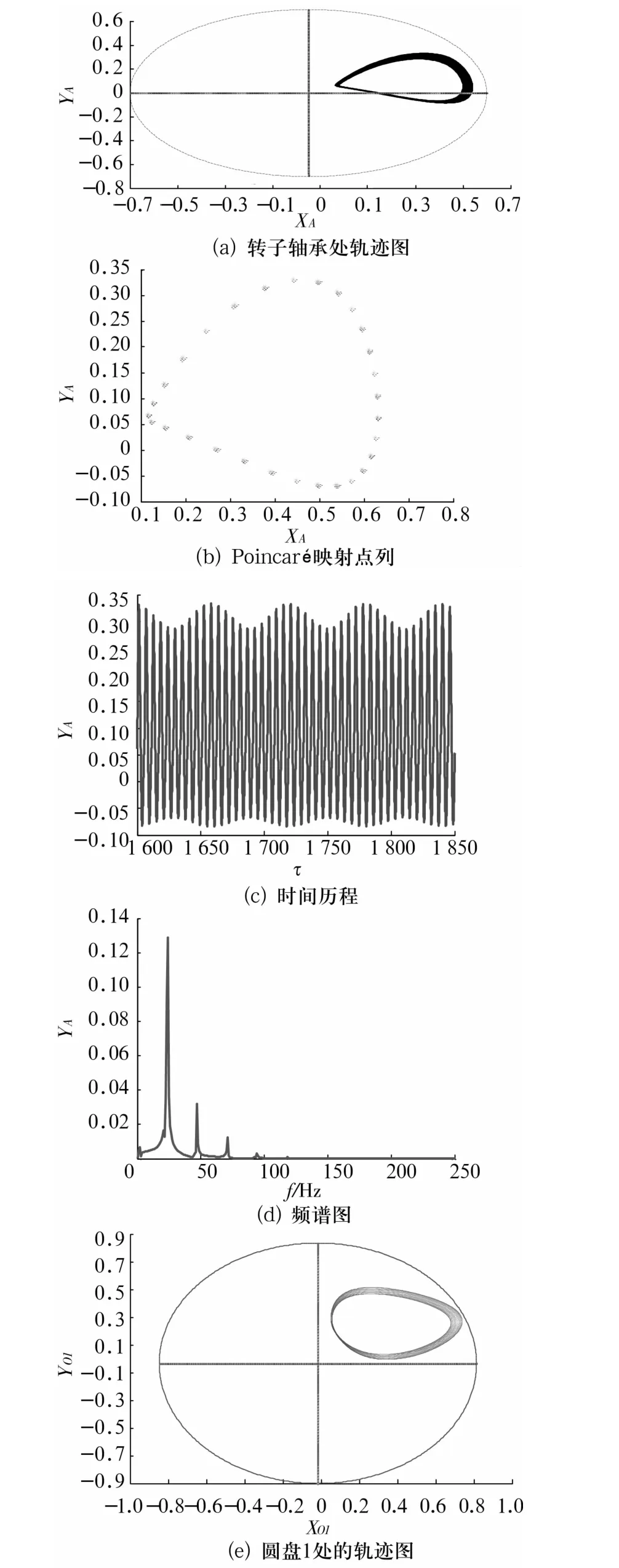
圖5 =0.95時轉子軸承處的軌跡圖、Poincaré映射圖、時間歷程、頻譜圖和圓盤1處的軌跡圖Fig.5 The orbit,Poincaré map,time series,spectrum of the rotor at bearing station and the orbit of disk 1 for=0.95

圖6 =0.95時圓盤分別繞x,y軸的擺角Fig.6 The swing angle of disks around the x and y axis for=0.95
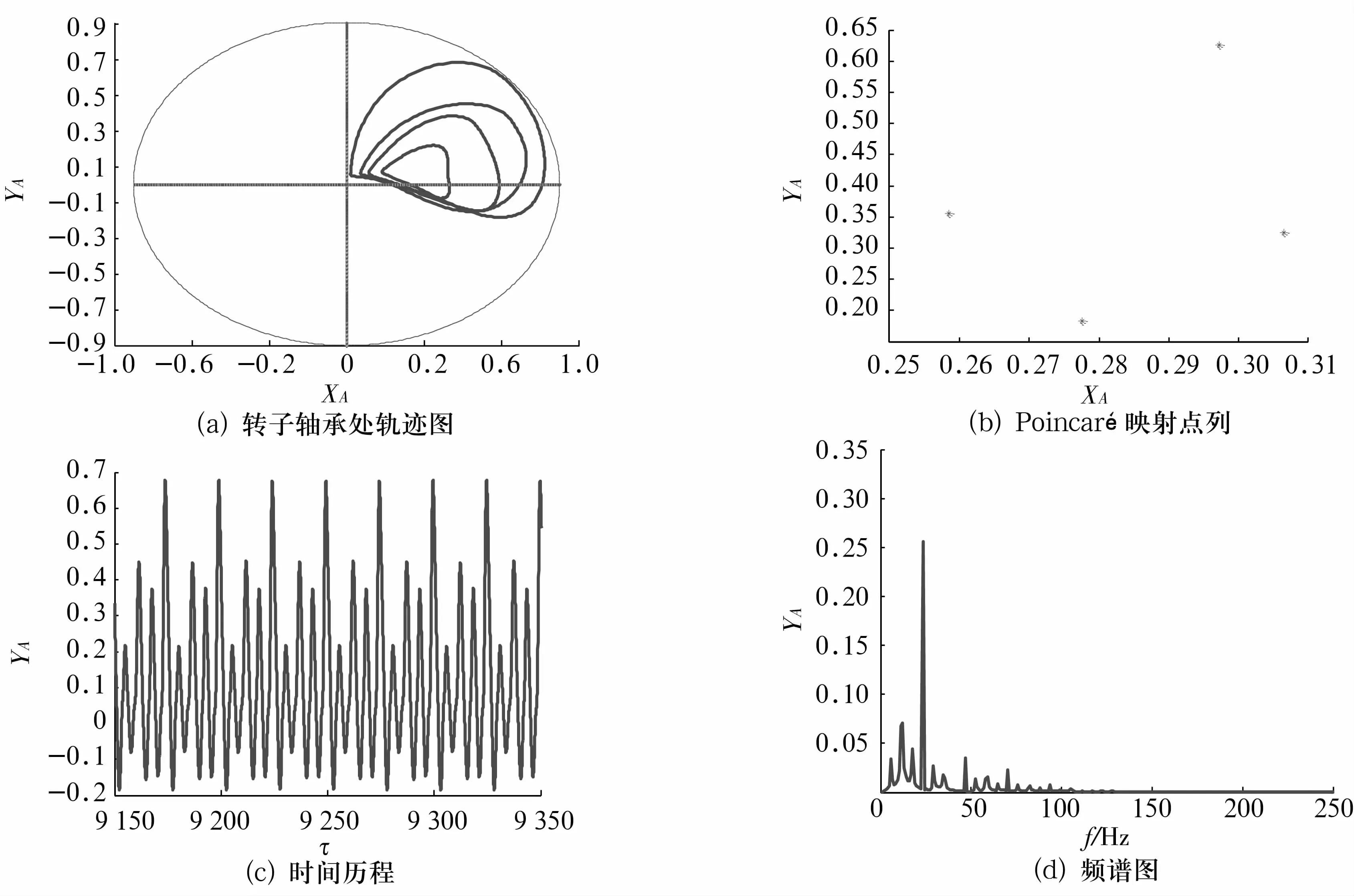
圖7 =1.04時轉子軸承處的軌跡圖、Poincaré映射圖、時間歷程和頻譜圖Fig.7 The orbit,Poincaré map,time series and spectrum of the rotor at bearing station for=1.04
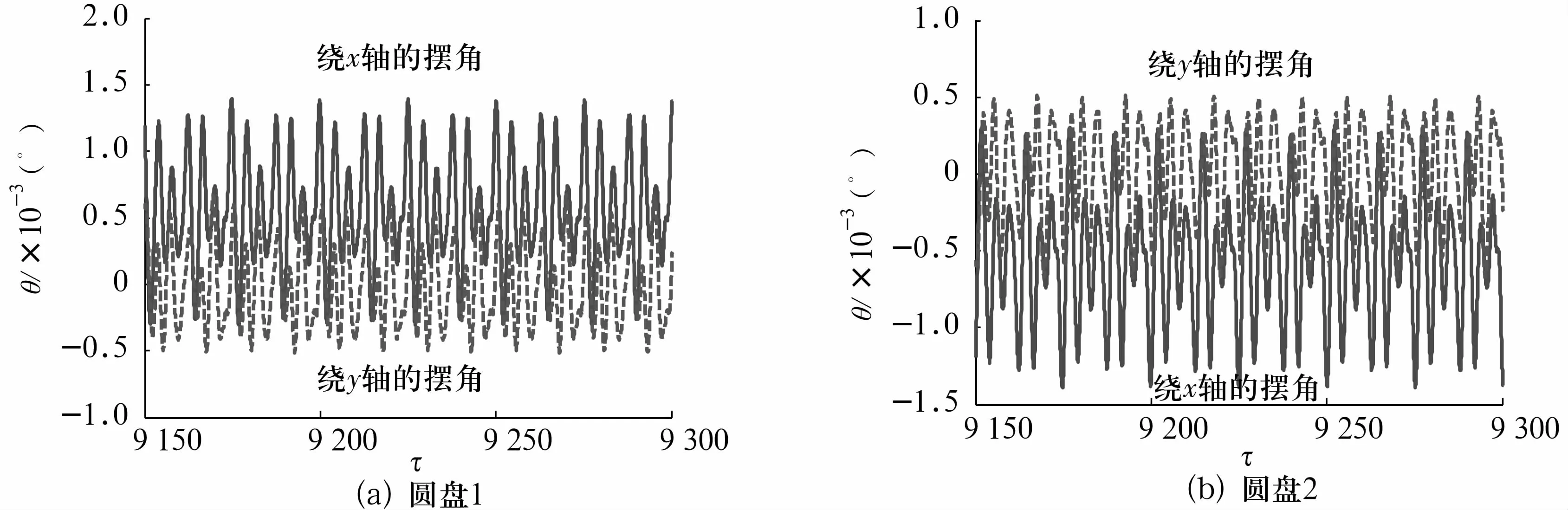
圖8 =1.04時圓盤繞x,y軸的擺角Fig.8 The swing angle of disks around the x and y axis for=1.04
以上計算步長取為h=2π/200,為了研究計算步長對系統非線性動力學行為的影響,以下步長分別取為 h=2π/400,2π/600,轉子軸承處和圓盤處的分岔圖如圖9、圖10所示。對比圖2、圖9和圖10可知,轉子系統運動的變化趨勢基本相同,但分岔點有所不同,隨著步長的減小,分岔點有少許增大,能夠考察的轉速范圍也增大,且轉子系統能夠表現出更豐富的非線性動力學現象。由此可以看出,計算步長的變化對于轉子系統運動具有一定影響。
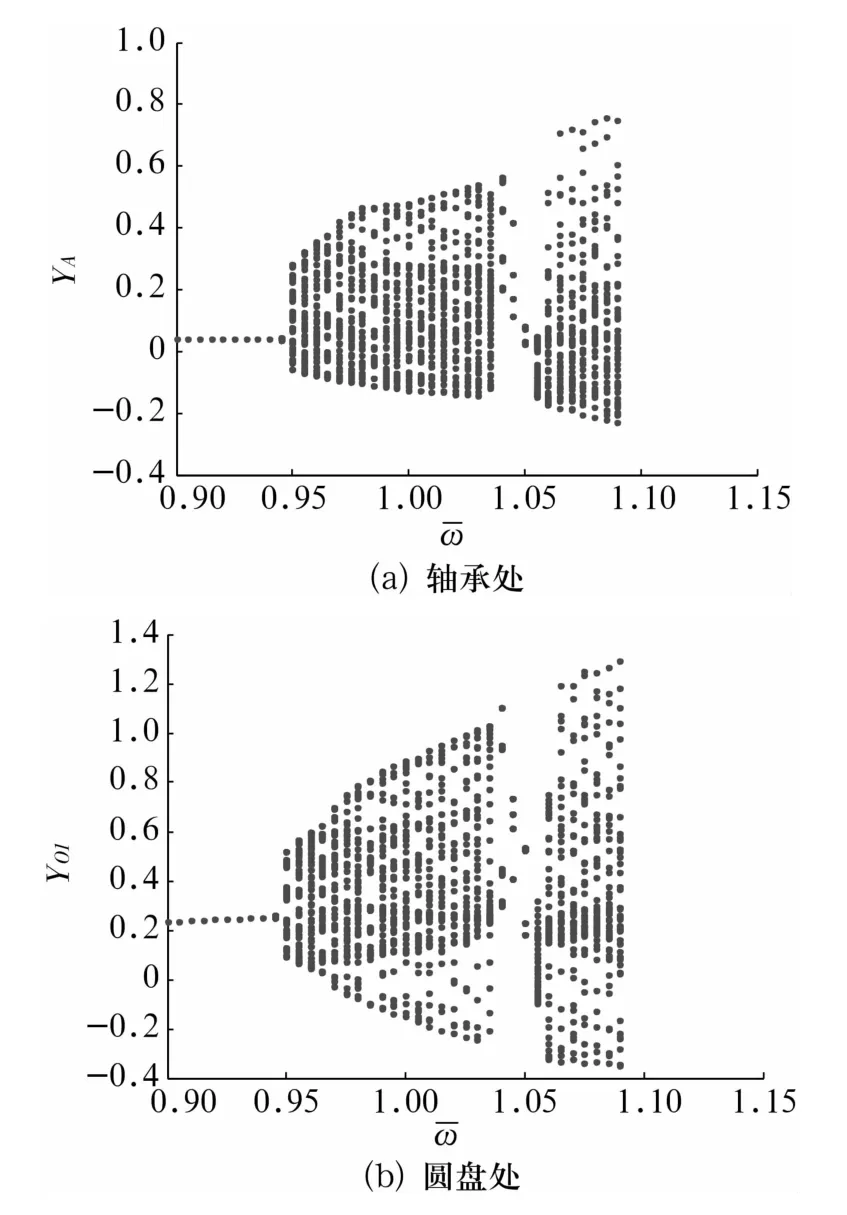
圖9 h=2π/400時轉子軸承和圓盤處y方向位移隨轉速的運動分岔圖Fig.9 Bifurcation diagram of y versus at bearing station and disk stations for h=2π/400
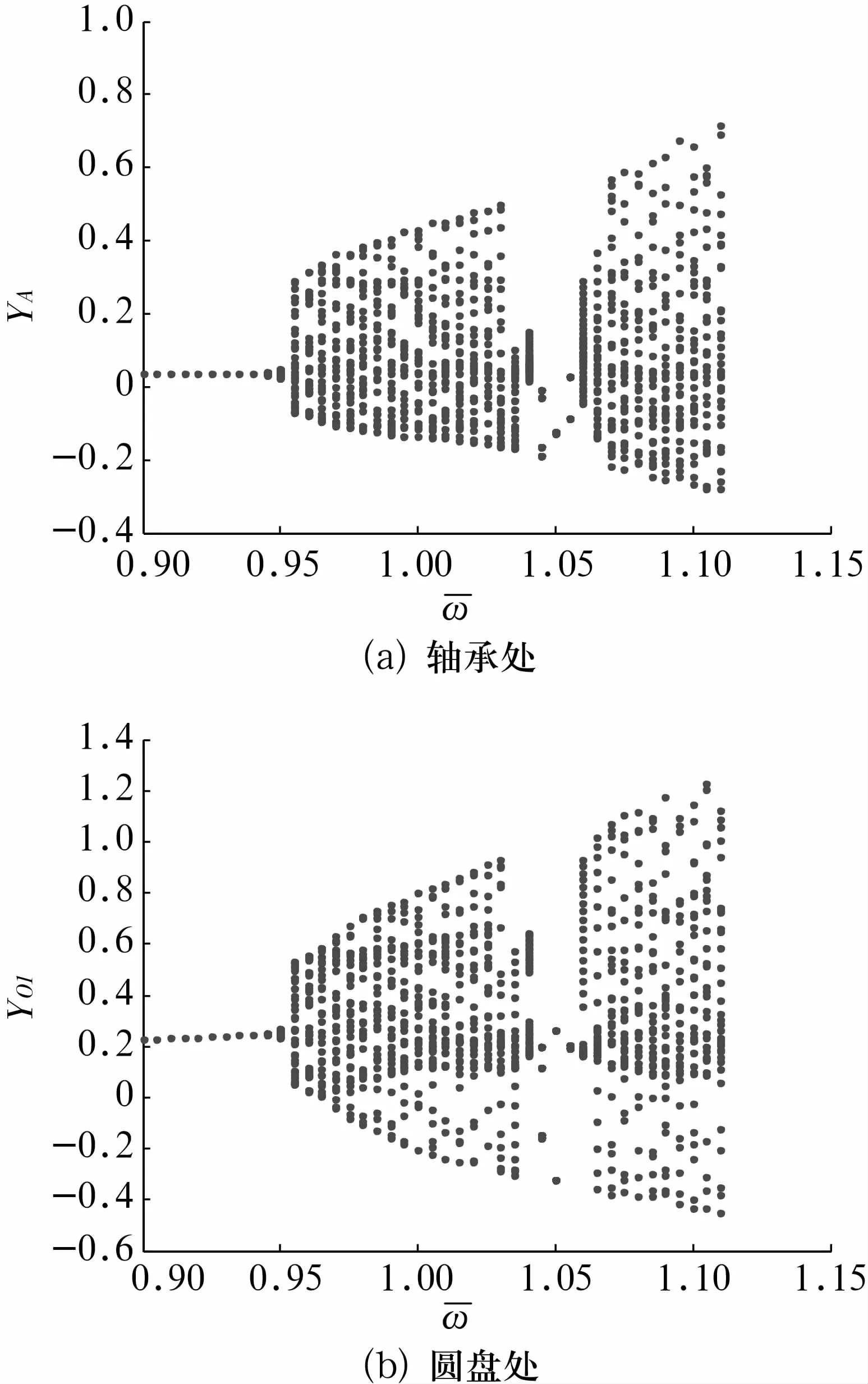
圖10 h=2π/600時轉子軸承和圓盤處y方向位移隨轉速的運動分岔圖Fig.10 Bifurcation diagram of y versus at bearing station and disk stations for h=2π/600
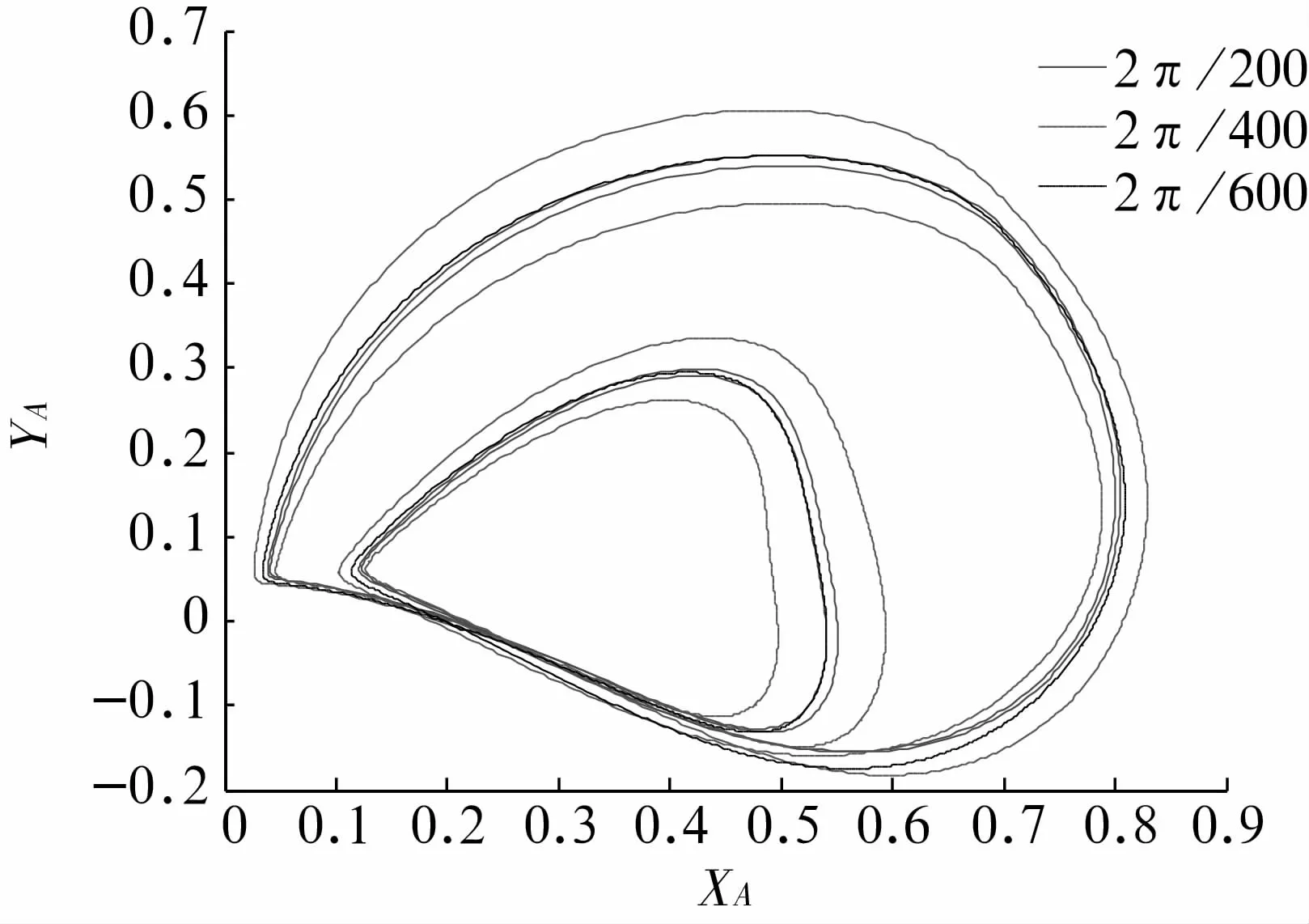
圖12 =1.05時3種步長下軸承處軌跡Fig.12 Comparison between the three steps at bearing station for=1.05
根據計算結果可以看出,計算步長對非周期運動影響較大,故從分岔點附近開始要縮小計算步長。在周期運動階段,取不同的步長轉子的運動軌跡有一定差別,但可以適當加大計算步長。
4 結束語
提出了一種改進的精細積分法,將其與常用的Newmark法、Wilson-θ法進行比較,發現該方法的計算結果比Newmark法和Wilson-θ法更接近精確解,驗證了其可靠性。
運用改進的精細積分法計算拉桿轉子系統的非線性動力學響應,從計算結果看出,該拉桿轉子系統存在豐富的非線性運動現象。同時研究了拉桿轉子圓盤的擺動,當轉子系統處于準周期運動的情況下,圓盤的擺角隨時間發散,最終導致轉子碰壁。而其他情況下,圓盤的擺角均隨時間呈周期性變化。
分析了計算步長對轉子系統運動的影響,從計算結果可看出,計算步長對于轉子系統非周期運動階段的影響較大,故在非周期階段應當采用較小的計算步長。在周期運動階段,即使其他參數都相同,采用不同的計算步長,轉子的運動軌跡仍有一定差別。計算步長對轉子系統的影響有待進一步深入研究。

