磁懸浮儲能飛輪振動狀態監測研究

薛曉川,王志強

(北京航空航天大學儀器科學與光電工程學院，北京 100191)

磁懸浮儲能飛輪振動狀態監測研究

薛曉川,王志強

(北京航空航天大學儀器科學與光電工程學院，北京 100191)

針對磁懸浮儲能飛輪系統的不平衡振動會影響轉子穩定運轉和系統正常工作的問題，對其擾動原因進行研究。通過建立含有轉子不平衡量的廣義干擾方程和磁懸浮飛輪動力學方程，對不平衡振動中的同頻、倍頻及模態分量進行理論分析。設計并實現了一套基于LabVIEW-DAQ的磁懸浮飛輪振動狀態監測系統，完成對儲能飛輪振動信號的實時采集、處理和顯示，實現了飛輪的振動狀態監測,并對一臺300 kW儲能飛輪進行試驗驗證。針對儲能飛輪工作的強電環境引起的信號噪聲，對原始信號進行小波閾值消噪處理。對消噪后的振動信號進行頻域分析，獲取某一轉速下飛輪的振動頻譜圖和不同轉速下飛輪振動信號的三維瀑布圖。試驗結果表明，該飛輪振動頻譜中存在穩定的飛輪旋轉頻率成分及其倍頻分量。該系統操作簡單，通用性強，具有一定的市場前景和應用價值。

儲能飛輪； 磁懸浮； 不平衡振動； 頻率成分； 數據采集； 小波消噪； 頻域分析； 狀態監測

0 引言

飛輪儲能技術作為一種新型儲能方式，以其高效、環保等優勢，具有廣泛的發展前景，并已在電網系統、軌道交通等領域發揮了巨大作用[1]。其原理是通過飛輪升降速，實現電能的存儲和釋放。相比機械軸承，磁軸承具有無摩擦、體積小、長壽命等特點[2]，將磁軸承應用于儲能飛輪系統是近幾年的研究熱點。

磁懸浮儲能飛輪工作時常伴有不平衡振動，會影響其工作性能，嚴重時甚至會引起飛輪失穩。對振動源進行識別和監測，已成為飛輪研究的重要問題。文獻[3]、文獻[4]中的飛輪振動測試系統，能夠實現小型反作用力飛輪的振動監測，但不適用于大型儲能飛輪。文獻[5]采用廣義Lagrange-Maxwell方程，從機電耦合特性的角度，對磁懸浮飛輪系統振動進行了理論分析和仿真驗證，但缺乏試驗驗證。

本文針對磁懸浮飛輪的不平衡振動問題，通過建立廣義干擾和轉子動力學模型，對振動源中的同頻、倍頻和模態分量進行理論分析，設計并實現了一套基于LabVIEW-DAQ的飛輪振動監測系統，以識別振動源中的各個分量并進行分析，為飛輪的故障診斷和狀態預測提供依據。

1 磁懸浮飛輪振動特性分析

儲能飛輪作為復雜的機電耦合系統，其振動原因較為復雜，但具有基本相同的表現形式。根據其頻域特征，可主要劃分為同頻分量、倍頻分量和模態分量。現通過建立數學模型的方法，對引起磁懸浮飛輪轉子不平衡的各種分量進行分析。

1.1 飛輪振動中的同頻分量

磁懸浮飛輪正常工作時，振動成分中存在同頻分量，其頻率等于飛輪的轉動頻率，且振動幅值較大。通過建立廣義干擾和轉子動力學模型的方法，對其影響因素進行分析。轉子廣義干擾示意圖如圖1所示。以飛輪質心O為坐標原點建立空間直角坐標系，Z軸為轉子轉軸，X平面、Y平面過原點且與Z軸互相垂直。X軸、Y軸方向隨轉子旋轉而不斷變化。

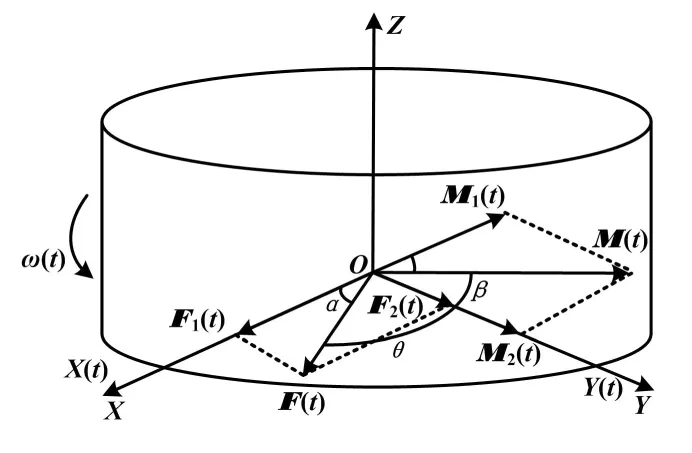
圖1 轉子廣義干擾示意圖

轉子不平衡量是引起飛輪不平衡振動的重要原因，這源于加工制造工藝的限制,可以通過轉子動平衡校正來減小，但無法徹底消除。其表現形式為飛輪工作時旋轉主軸和慣性主軸不重合。磁懸浮飛輪的工作原理是將飛輪轉子懸浮于轉子的幾何軸，因此當飛輪繞轉子幾何軸旋轉時，飛輪的慣性主軸就會繞幾何軸轉動[6]，產生慣性力和慣性力偶矩使轉子發生不平衡振動。現從廣義干擾的角度，對飛輪的不平衡振動原因進行分析。

根據不平衡的定義可知，不平衡量存在時的一種表現形式為力和力矩的廣義干擾作用于飛輪[7]。ω(t)為飛輪的轉動角頻率；F(t)為所有引起飛輪振動的轉子慣性離心力的合力，即主矢；M(t)為慣性離心力矩的合力偶矩，即主矩；θ為初始相位差。F(t)和M(t)的方向隨轉子的轉動而改變，其頻率均等于飛輪的旋轉頻率。分別將F、M在X軸、Y軸上進行分解，得：

(1)

(2)

將主矢和主矩的共同作用看作一種廣義干擾，在X軸、Y軸上進行分解，分量為Ax(t)和Ay(t)。由于主矢和主矩的頻率均等于飛輪轉頻，故廣義干擾分量的頻率也與飛輪旋轉頻率相等。設其幅值分別為Ax0和Ay0，φ為干擾量相對于坐標系的初始相位，則有：

(3)

在不考慮磁軸承控制的前提下，單獨分析引入轉子不平衡激勵帶來的影響。此時可將飛輪簡化為一個單自由度的線性系統。廣義干擾Ax(t)、Ay(t)為系統的激勵源，可以看出在X方向和Y方向上，會產生穩定的同頻分量，表現為飛輪以等同于轉頻的頻率振動。

此外，轉子的不平衡量還會激發磁軸承電流剛度力和位移剛度力中的同頻分量。在磁懸浮飛輪系統中，轉子的不平衡量會導致磁軸承中心平面對應點的偏移。磁懸浮飛輪動力學簡化圖如圖2所示。

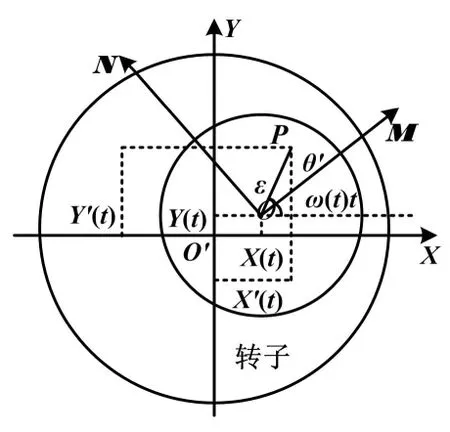
圖2 磁懸浮飛輪動力學簡化圖

圖2中：外圓為徑向磁軸承，內圓為飛輪轉子。

以磁軸承的幾何中心O′為坐標原點建立直角坐標系，X軸、Y軸的方向與位移傳感器的安裝方向一致。由于轉子不平衡量的存在，使得其幾何軸和慣性主軸不重合。轉子以ω(t)的轉速作逆時針旋轉,O為轉子幾何中心，P為轉子質心，ε為OP向量的模長。以O為坐標原點，建立轉子的轉動坐標系，對應坐標軸為M和N，且方向隨轉子轉動時刻變化。OP向量與M軸的夾角為θ′。t時刻M軸與X軸夾角為ω(t)t。X(t)和Y(t)為轉子的幾何中心相對于磁軸承幾何中心的位移分量，為磁軸承的控制量。X′(t)和Y′(t)為轉子的質心相對于磁軸承幾何中心的位移分量。

由圖2中的幾何關系，得到如下方程組：

(4)

磁懸浮飛輪正常工作時的控制電流一般小于偏置電流，此時可得到磁懸浮飛輪徑向轉子動力學方程，如式(5)所示。

(5)

式中：Fx、Fy分別為磁軸承在X和Y方向的控制力；μ為真空磁導率；n為線圈匝數；S為磁鐵的橫截面積；σ為磁鐵磁極偏角；iy為偏置電流；ix、iy分別為X和Y方

向的控制電流；X0、Y0分別為轉子在平衡位置時X方向和Y方向的位移。

當轉子在平衡位置處的位移X=X0、Y=Y0時，可將方程組作線性化處理，分別對電流、位移求偏導，在X、Y趨于0的條件下作一階Taylor展開,得：

(6)

化簡得：

(7)

實際控制時，控制電流為轉子位移的PID函數，因此,不平衡引入的擾動會同時引入到位移項和電流項之中，代入式(6)可得:

(8)

由此可知，轉子的不平衡量在磁軸承控制的過程中引入同頻干擾。

1.2 飛輪振動中的倍頻分量

在對飛輪進行磁懸浮時，需根據位移傳感器的測量值對磁軸承的軸向和徑向位移進行控制。飛輪倍頻干擾主要由傳感器諧波噪聲引起，最終表現為對磁軸承控制電流項的影響。其數學表達式為：

(9)

式中：λx、λy分別為位移傳感器引入的噪聲干擾；λx,i、λy,i分別為各次諧波對應的干擾幅值；Ψx,i、Ψy,i分別為各次諧波干擾項所對應的初始相位。

將λx、λy代入式(8),可得：

(10)

由此可知，傳感器倍頻擾動會在磁軸承轉子的動力學方程中引入倍頻分量。

1.3 飛輪振動中的模態分量

除同頻、倍頻擾動外，模態分量也是引起飛輪不平衡振動、制約飛輪轉速的重要原因。這種由模態分量引起的飛輪擾動被稱為結構模態振動，它取決于飛輪系統的固有頻率。在飛輪轉速范圍內，存在轉子固有頻率和飛輪旋轉頻率相等的情況，即引發共振[8]。系統中的共振頻率由質量、剛度和衰減系數決定[9]。因此，為了避免因不平衡激勵引發的共振現象，應使飛輪轉頻盡量遠離飛輪的固有頻率。飛輪轉子的各階模態固有頻率可由有限元分析軟件計算得到。

2 飛輪振動狀態監測系統設計

為了獲取某一時刻磁懸浮飛輪的振動數據，本文設計了一套飛輪振動狀態監測系統，能夠實現振動信號的采集、處理、顯示和記錄。后期可通過對數據進行小波閾值去噪、快速傅里葉變換(fast Fourier transform,FFT)頻譜分析、三維瀑布圖分析的方法進行驗證，以識別飛輪不同狀態下的振動對應頻率，進而判斷飛輪的運行狀態。

總體設計思路為：通過固連在飛輪殼體上的多個壓電式加速度計，獲取飛輪的振動信號。振動信號通過恒流適配器，傳送到集成有數據采集卡的工控機中。使用編寫的上位機軟件對其進行控制，實現數據的采集，處理和記錄。系統總體設計框圖如圖3所示。

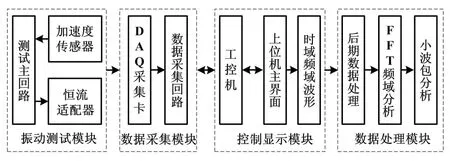
圖3 系統總體設計框圖

2.1 系統硬件

振動監測系統的硬件部分主要由工控機、NI PCI-6255數據采集卡、CT5200恒流適配器和CT-1050LC加速度計等模塊實現。硬件部分設計框圖如圖4所示。

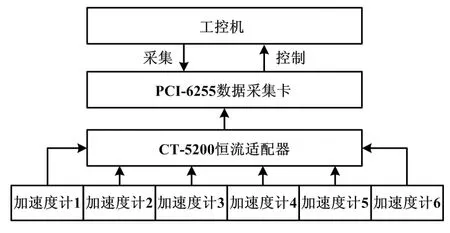
圖4 硬件部分設計框圖

數據采集卡選用NI公司的PCI-6255數據采集卡，采用擁有較高的分辨率和敏感度的高度精M系列模塊。傳感器安裝位置如圖5所示。

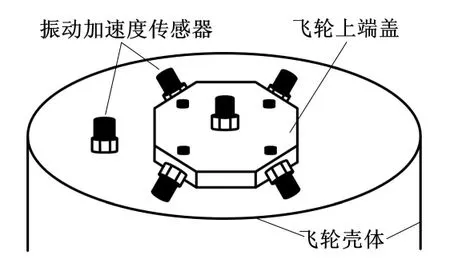
圖5 傳感器安裝位置示意圖

測量敏感元件選用CT1050系列壓電式加速度傳感器。該傳感器基于壓電效應原理，具有頻域寬、靈敏度高、橫向靈敏度小等優點。測試系統使用六個壓電式加速度傳感器與飛輪殼體固連。兩組互相正交、水平放置，測量飛輪徑向方向振動；兩個傳感器豎直放置，測量輪體軸向方向振動。

2.2 系統軟件

LabVIEW虛擬儀器具有靈活性好、開發費用低、周期短、人機交互性好的特點。本試驗系統軟件部分采用圖形化編程軟件LabVIEW平臺中的DAQ數據采集功能[10]。其流程是：先設定數據采集的工作狀態，如通道數、采樣率、數據記錄文件路徑等；再運行振動信號數據采集程序，并將各個通道振動信號的時域和頻域波形圖實時顯示在主面板上。軟件部分設計框圖如圖6所示。

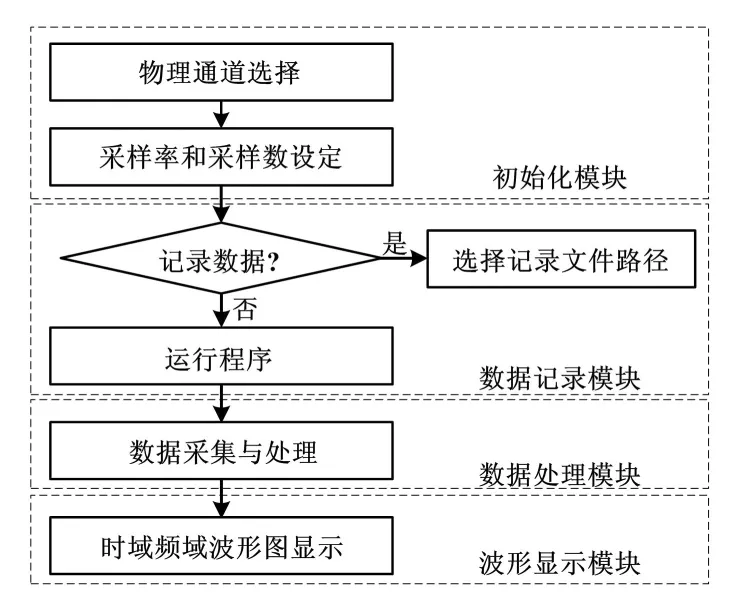
圖6 軟件部分設計框圖

3 試驗驗證與數據分析

利用試驗室研制的一臺300 kW磁懸浮儲能飛輪進行試驗驗證。其主要技術指標為：額定功率為300 kW，額定轉速為30 000 r/min，整體質量為855 kg，轉子直徑為314 mm，位移傳感器分辨率為2.6×10-3V/μm。

3.1 飛輪模態分析

首先分析振動模態分量的影響。在實際飛輪系統中，當飛輪工作頻率與其固有頻率相等時，會產生共振現象，使系統無法發揮最大效能。使用ANSYS軟件對飛輪轉子進行有限元分析，可得到X方向一階、二階固有頻率為697.6 Hz和1 844.4 Hz，對應振型分別為X方向一階、二階彎曲。由于儲能飛輪的額定轉速為30 000 r/min(轉頻為500 Hz)，低于轉子的一階彎曲模態頻率，因此可以將其視為剛性轉子，忽略擾動中模態分量的影響。

3.2 小波閾值去噪

對監測系統獲取的飛輪振動信號進行數學處理。由于實測信號中不可避免地存在噪聲，為了保證試驗結果的準確性，可運用小波變換的自適應閾值方法對振動原始信號進行消噪處理，提取信號中的有用成分。具體實現手段是先對原始信號進行小波變換，得到小波變換系數計算閾值；舍去小于閾值的變換系數，對于大于閾值的變換系數，采用軟閾值方法進行處理；作小波逆變換實現信號的還原，實現圖像去噪的目的[11]。具體實現步驟如下。

①選取DB4和Sym4小波基對原始振動信號進行2層分解。

②計算相應子空間的均值、中值和均方根，確定最優閾值。

③對大于閾值的系數作軟閾值處理。

④小波包重構信號恢復。

振動信號時域波形圖如圖7所示。對比圖7(a)和圖7(b)可以發現，小波去噪效果明顯，驗證了該方法的有效性和正確性。

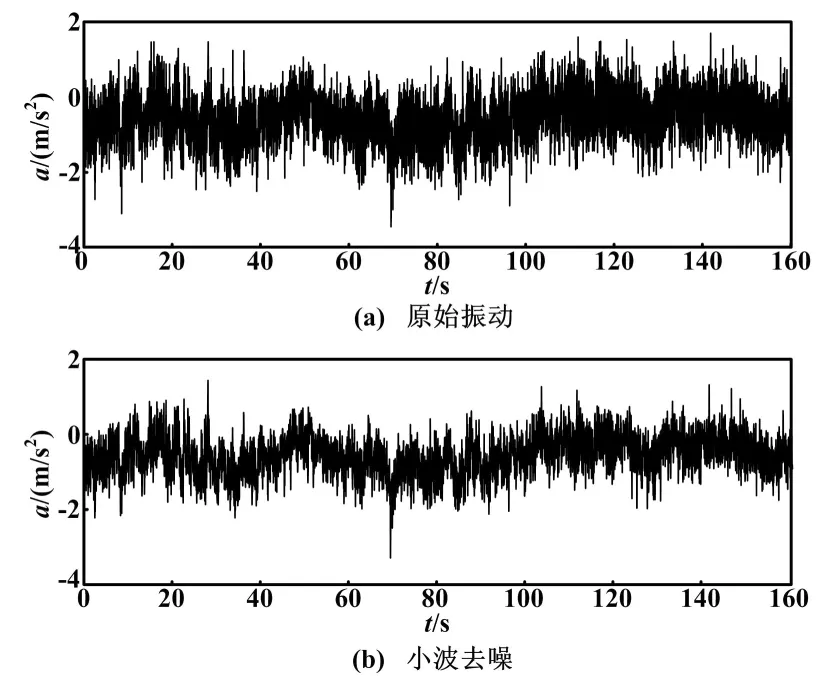
圖7 振動信號時域波形圖

3.3 FFT頻譜分析

頻域特性是數字信號的基本特性。從頻域角度對信號進行分析與處理，容易對信號的特性進行深入了解[12]。振動信號頻譜分析法是在通用信號處理理論基礎上發展起來的，它是診斷工作的依據[13]。傅里葉變換是一種積分變換，它建立了信號時域與頻域聯系的紐帶。

借助MATLAB軟件對采集到的小波去噪后的信號進行FFT處理，得到振動信號的頻域圖。通過同一轉速下某傳感器測量飛輪振動信號頻域圖，進行頻域分析，可以得出各個頻率下對應的振動幅值大小，識別對應的特征頻率。將對應的飛輪轉速、頻率、振幅繪制成三維瀑布圖，分析飛輪的振動幅值大小及其對應頻率隨轉速的變化規律。在對徑向方向傳感器測量值進行頻譜分析時，盡管X方向和Y方向的受力以及磁軸承的剛度及阻尼略有不同，但振動的本質規律相同。因此取X方向某一傳感器的測量結果作FFT并繪制頻譜圖。飛輪轉速為4 500 r/min時的頻域波形圖如圖8所示。

不考慮信號頻譜中直流分量的影響，對磁懸浮飛輪的振動頻率進行分析。

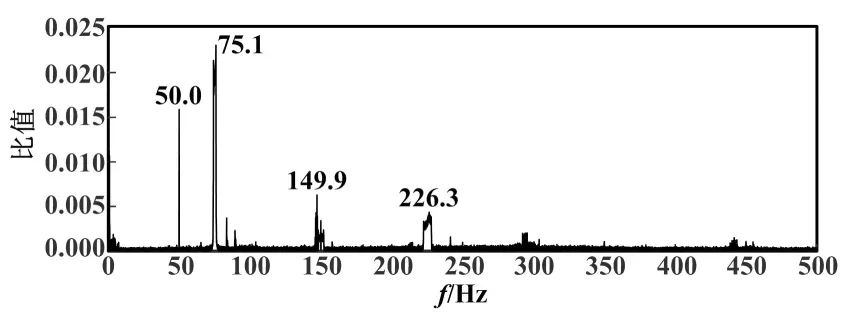
圖8 振動頻譜圖(4 500 r/min)

由圖8可以明顯地看出，系統的主振頻率為75.1 Hz，基本等于飛輪在4 500 r/min狀態時的同頻振動頻率，誤差為0.13%，其振動幅值達到了0.023 07g(g為重力加速度)。其振動源是由轉子不平衡量引起的慣性離心力和力矩，以及磁軸承電流剛度力和位移剛度力中的同頻分量。這些因素的疊加會引起飛輪系統的同頻振動。

同時，從圖8還可以看出，系統中存在倍頻振動分量，即轉頻的高次諧波。其振動幅值小于同頻分量，以二倍頻、三倍頻較為明顯。該倍頻振動分量與磁軸承位移傳感器引入的諧波噪聲分量有關。信號在50 Hz左右處存在穩定的分量，且幅值較大。該分量由工頻電信號干擾造成，實際分析時可略去。如需避免工頻干擾，可以采取使用抗電磁干擾的采集卡等措施，改善系統性能。

儲能飛輪徑向振動信號在某轉速范圍內的三維轉子降速瀑布圖如圖9所示。

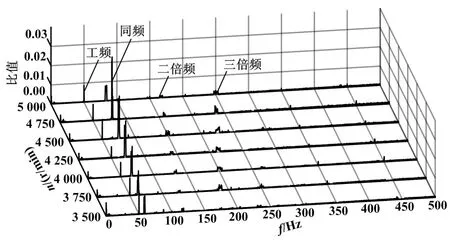
圖9 三維轉子降速瀑布圖

在磁懸浮飛輪自由降速的過程中，忽略直流分量和工頻干擾的影響，系統的振動主頻是飛輪的工作轉速頻率，且振動幅值最大。采用提高轉子動平衡試驗精度等方法減小此同頻振動量。除此之外，還可以明顯地看出，系統中存在轉頻的倍頻成分，以2次、3次諧波為主。通過降低位移傳感器諧波噪聲，可減小倍頻分量對系統的影響。同時，應保證系統的額定工作轉速遠離計算得到的轉子一階固有頻率，防止共振現象的發生。試驗現象與之前的理論分析相吻合，同時也表明飛輪振動狀態監測系統能夠較好地完成實時采集、處理和監測的預期功能。

4 結束語

本文以磁懸浮飛輪的不平衡振動為研究對象，分析了飛輪振動成分中的同頻、倍頻和模態分量。在廣義干擾方程和轉子動力學方程的基礎上，闡述了各種振動分量的原因和影響因素。設計并實現了一種飛輪振動狀態監測系統，對飛輪的振動數據進行實時的采集、處理和顯示。后期對振動數據進行小波閾值消噪和頻譜分析。試驗結果表明，磁懸浮飛輪正常工作時，存在穩定的同頻和倍頻振動分量。驗證了理論分析的合理性和本系統的可行性，為飛輪故障診斷和狀態預測提供依據。

[1] 陳廣宇,張華東,于寶鑫,等.飛輪儲能關鍵技術及其應用[J].電氣應用,2015,34(24):53-58.

[2] 潤章,朱熀秋,朱利東.磁懸浮飛輪軸向混合磁軸承參數設計及分析[J].機械設計與研究,2015,31(1):39-43.

[3] TANIWAKI S,OHKAMI Y.Experimental and numerical analysis of reaction wheel disturbances[J].JSME International Journal,2003,46(2):519-526.

[4] OH H S,CHEON D I.Precision measurements of reaction wheel disturbances with frequency compensation process[J].Journal of Mechanical Science and Technology,2005,19(1):136-143.

[5] 陳峻峰,劉昆,梁文杰,等.磁懸浮飛輪儲能系統機電耦合非線性動力學研究[J].動力學與控制學報,2013,11(3):225-234.

[6] 劉彬,房建成,劉剛,等.磁懸浮飛輪不平衡振動控制方法與試驗研究[J].機械工程學報,2010,46(12):188-194.

[7] 王全武,虎剛.飛輪振動頻譜特征的初步理論分析和驗證[J].空間控制技術與應用,2008,34(4):42-46.

[8] 臧孝華,王全武.振動測試技術在飛輪動平衡調整中的應用[J].新技術新工藝,2013(1):51-53.

[9] 王光軍,胡萬明.高速回轉機械振動產生的原因、測試標準與防治[J].氯堿工業,2006(5):44-44.

[10]王平,楊濤,侯守全,等.LabVIEW中DAQ數據采集系統設計[J].自動化儀表,2015,36(7):31-33.

[11]朱希安.小波分析及其在數字圖像處理中的應用[M].北京：電子工業出版社,2012:88-95.

[12]劉小群,周云波.基于Matlab的DFT及FFT頻譜分析[J].山西電子技術,2010(4):48-49.

[13]梅海青,馮毅.基于振動信號頻譜分析的回轉機械故障診斷方法[J].流體機械,2003,31(1):29-31.

Study on the Vibration Condition Monitoring
for Magnetic Levitation Energy Storage Flywheel

XUE Xiaochuan,WANG Zhiqiang
(College of Instrument Science and Optoelectronic Engineering,Beihang University,Beijing 100191,China)

In magnetic levitation energy storage flywheel system,the unbalanced vibration may influence the stability of the rotor and the normal operation of system;aiming at these problems,the reasons of the disturbance are studied.Through establishing the generalized disturbance equation containing unbalance quantity of rotor,and the dynamics equation of magnetic levitation flywheel,the theoretical analysis of the same frequency,double frequency and modal components in the unbalance vibration is carried out.A vibration condition monitoring system based on LabVIEW-DAQ for the magnetic levitation flywheel is designed and implemented.With this system,real-time acquisition,processing and display of the flywheel vibration signal can be completed,and the vibration condition monitoring of flywheel is implemented,and the experimental verification for a certain 300 kW energy storage flywheel is conducted.Aiming at the signal noise caused by the strong electric working environment of flywheel,the original signals are processed with wavelet threshold denosing,and the frequency domain syslysis is accomplished for the vibration signal after denoising,to obtain the vibration spectrum of the flywheel at a certain speed; and the three dimensional waterfall diagram of flywheel vibration signal under different speeds.The experimental results show that in the vibration spectrum of the flywheel,both the stable flywheel rotating frequency component and the double frequency component exist.The system is simple and versatile,so it has good market prospect and application value.

Energy storage flywheel; Magnetic levitation; Unbalance vibration; Frequency component; Data acquisition; Wavelet manic elimination; Frequency domain analysis; Condition monitoring

薛曉川(1993—)，男，在讀碩士研究生，主要從事電機伺服控制技術、集成電路設計、數字信號處理等方向的研究。 E-mail：sleepingriver@163.com。 王志強(通信作者)，男，博士，講師，主要從事先進空間慣性執行機構驅動控制技術、交流永磁電機控制技術、電力電子技術的研究。E-mail：wangzhiqiang@buaa.edu.cn。

TH825;TP806+.1

A

10.16086/j.cnki.issn1000-0380.201707022

修改稿收到日期：2017-01-31