輪胎帶束層結(jié)構(gòu)變化對(duì)固有頻率的影響研究

朱新靜，朱作勇，趙鵬翔，馮希金

（賽輪金宇集團(tuán)股份有限公司，山東 青島 266045）

輪胎是汽車(chē)與地面接觸的唯一部件，它的動(dòng)力學(xué)特性影響汽車(chē)的動(dòng)力性、經(jīng)濟(jì)性、操縱穩(wěn)定性和噪聲。

研究輪胎在各種復(fù)雜激勵(lì)下的振動(dòng)和噪聲響應(yīng)特性，首先要研究輪胎的固有頻率和模態(tài)特性，常用的研究方法有試驗(yàn)方法[1-3]、解析方法和有限元分析方法[4-5]。

本研究基于Abaqus非線性有限元分析軟件建立三維輪胎的振動(dòng)模態(tài)分析方法，求出輪胎徑向各階振型，并進(jìn)行實(shí)際輪胎的振動(dòng)模態(tài)試驗(yàn)，分析輪胎結(jié)構(gòu)帶束層方案改變對(duì)輪胎固有頻率的影響規(guī)律，以期為后續(xù)整車(chē)配套過(guò)程中遇到的振動(dòng)和舒適性問(wèn)題提供解決思路。

1 輪胎固有頻率和模態(tài)的有限元求解方法

1.1 動(dòng)力學(xué)系統(tǒng)的有限元求解方程

根據(jù)動(dòng)力學(xué)系統(tǒng)的基本理論，求解動(dòng)力學(xué)響應(yīng)的基本方程為

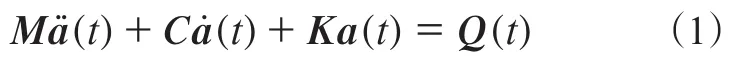
如果忽略阻尼的影響，則運(yùn)動(dòng)方程簡(jiǎn)化為

若運(yùn)動(dòng)方程（2）的右端項(xiàng)為零，則可以進(jìn)一步簡(jiǎn)化為

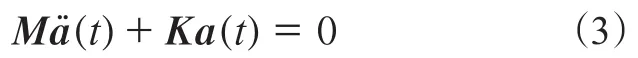
運(yùn)動(dòng)方程（3）為系統(tǒng)的自由振動(dòng)方程，可以求解出系統(tǒng)的無(wú)阻尼固有頻率和模態(tài)。

運(yùn)動(dòng)方程（1）的求解方法有直接積分法和振型疊加法，考慮到計(jì)算成本和計(jì)算效率，通常采用振型疊加法。振型疊加法的基本思路是先求解系統(tǒng)的自由振動(dòng)方程（3），得到系統(tǒng)的無(wú)阻尼固有頻率和固有振型，然后用固有振型對(duì)運(yùn)動(dòng)方程（1）進(jìn)行交換，最后對(duì)各自由度的運(yùn)動(dòng)方程進(jìn)行積分并疊加，從而求得。

1.2 固有頻率和模態(tài)的有限元求解方法

運(yùn)動(dòng)方程（3）的求解有4種方法：矩陣反迭代法、子空間迭代法、Ritz向量直接疊加法和Lanczos向量直接疊加法。矩陣反迭代法算法簡(jiǎn)單，比較適合求解數(shù)目較少的特征值的情況，子空間迭代法是將矩陣反迭代法推廣應(yīng)用于同時(shí)利用若干個(gè)向量進(jìn)行迭代的情況，即用于求解更多特征值的情況。而Ritz向量直接疊加法和Lanczos向量直接疊加法的共同特點(diǎn)是直接生成一組Ritz向量或者Lanczos向量，對(duì)運(yùn)動(dòng)方程進(jìn)行縮減，然后通過(guò)求解縮減的運(yùn)動(dòng)方程的特征值問(wèn)題，進(jìn)而得到原系統(tǒng)的特征解，從而避免了矩陣反迭代法和子空間迭代法的迭代步驟，具有更高的計(jì)算效率。本研究采用的是Lanczos向量直接疊加法。

1.3 輪胎有限元模型

建立205/55R16光面輪胎動(dòng)力學(xué)有限元模型。輪胎二維有限元模型如圖1所示，將二維模型進(jìn)行周向旋轉(zhuǎn)形成如圖2所示的三維有限元模型。

圖1 輪胎二維有限元模型

圖2 輪胎三維有限元模型

采用標(biāo)準(zhǔn)輪輞，充氣壓力為250 kPa，輪胎負(fù)荷為零。

單元格類(lèi)型設(shè)定為減縮積分模式，即四角形單元設(shè)定為CGAX4R，三角形單元設(shè)定為CGAX3。橡膠材料屬性定義為Neo-Hooke模型，簾線材料屬性定義為線彈性模型。

1.4 徑向振動(dòng)模態(tài)仿真結(jié)果

輪胎的振動(dòng)行為較復(fù)雜，從其宏觀的振動(dòng)形態(tài)來(lái)看，大體可以分為徑向振動(dòng)模態(tài)、橫向振動(dòng)模態(tài)和周向振動(dòng)模態(tài)，本工作主要針對(duì)徑向振動(dòng)模態(tài)進(jìn)行研究。

徑向振動(dòng)模態(tài)是輪胎振動(dòng)的主要形式之一，反映了輪胎在不同振動(dòng)頻率下的徑向變形，與車(chē)輛的乘坐舒適性有很大關(guān)系。徑向各階振動(dòng)模態(tài)的仿真結(jié)果如圖3所示。

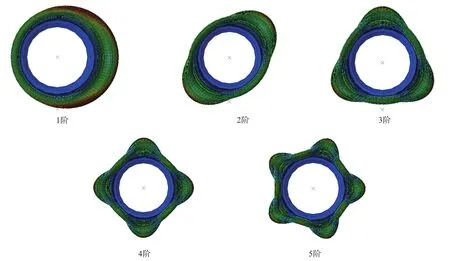
圖3 徑向各階振動(dòng)模態(tài)的仿真結(jié)果

2 輪胎固有頻率和模態(tài)的試驗(yàn)方法

2.1 振動(dòng)模態(tài)試驗(yàn)裝置

為了驗(yàn)證有限元分析結(jié)果，進(jìn)行輪胎振動(dòng)模態(tài)的測(cè)量試驗(yàn)。輪胎振動(dòng)模態(tài)試驗(yàn)裝置如圖4所示。

圖4 輪胎振動(dòng)模態(tài)試驗(yàn)裝置

試驗(yàn)采用單點(diǎn)激振、兩點(diǎn)響應(yīng)測(cè)振的方式。在輪胎的中心圓周上均勻設(shè)置24個(gè)測(cè)振位置，試驗(yàn)過(guò)程中通過(guò)移動(dòng)力錘的方法實(shí)現(xiàn)對(duì)這24個(gè)位置振動(dòng)信號(hào)的測(cè)量。本次試驗(yàn)采用單向加速度傳感器，每次試驗(yàn)可提取單一方向的加速度信號(hào)，根據(jù)更換傳感器的位置獲得徑向模態(tài)和橫向模態(tài)。

振動(dòng)模態(tài)試驗(yàn)裝置通常自帶信號(hào)處理軟件，可以直接得到各階固有頻率。

2.2 徑向振動(dòng)模態(tài)試驗(yàn)結(jié)果

徑向各階振動(dòng)模態(tài)的試驗(yàn)結(jié)果如圖5所示。

從圖5可以看出，仿真計(jì)算結(jié)果與試驗(yàn)結(jié)果吻合。

圖5 徑向各階振動(dòng)模態(tài)試驗(yàn)結(jié)果

2.3 不同帶束層結(jié)構(gòu)的輪胎方案

為了研究不同帶束層結(jié)構(gòu)對(duì)輪胎固有頻率的影響，選取205/55R16光面輪胎，改變輪胎帶束層的材質(zhì)、角度和寬度，采用仿真方法和室內(nèi)測(cè)試方法分析輪胎帶束層對(duì)輪胎固有頻率的影響規(guī)律，并對(duì)照仿真與室內(nèi)測(cè)試的結(jié)果，完善仿真方法，為后續(xù)研發(fā)預(yù)測(cè)奠定基礎(chǔ)。

表1列出了此次的所有設(shè)計(jì)方案，包括鋼絲材質(zhì)、帶束層寬度及帶束層角度。對(duì)比方案如下。

表1 輪胎設(shè)計(jì)方案匯總

（1）帶束層材質(zhì)對(duì)固有頻率的影響：1#—4#綜合對(duì)比；

（2）帶束層角度對(duì)固有頻率的影響：3#，5#和6#綜合對(duì)比；

（3）帶束層寬度對(duì)固有頻率的影響：3#，7#—9#綜合對(duì)比。

3 結(jié)果與討論

3.1 帶束層材質(zhì)對(duì)固有頻率的影響

表2示出了4種不同帶束層材質(zhì)輪胎的固有頻率模擬仿真計(jì)算結(jié)果和試驗(yàn)結(jié)果。

其中，4種材質(zhì)的彈性模量（E）數(shù)據(jù)對(duì)比為EA＝EB＜EC＜ED；4種材質(zhì)的單根面積數(shù)據(jù)對(duì)比為EA＝EB＜EC＜ED；4種材質(zhì)的單絲密度（EPI）數(shù)據(jù)對(duì)比為EC＝ED＜EA＜EB。

由表2可以看出，D材質(zhì)的試驗(yàn)結(jié)果和仿真結(jié)果固有頻率均低于其他3種材質(zhì)。

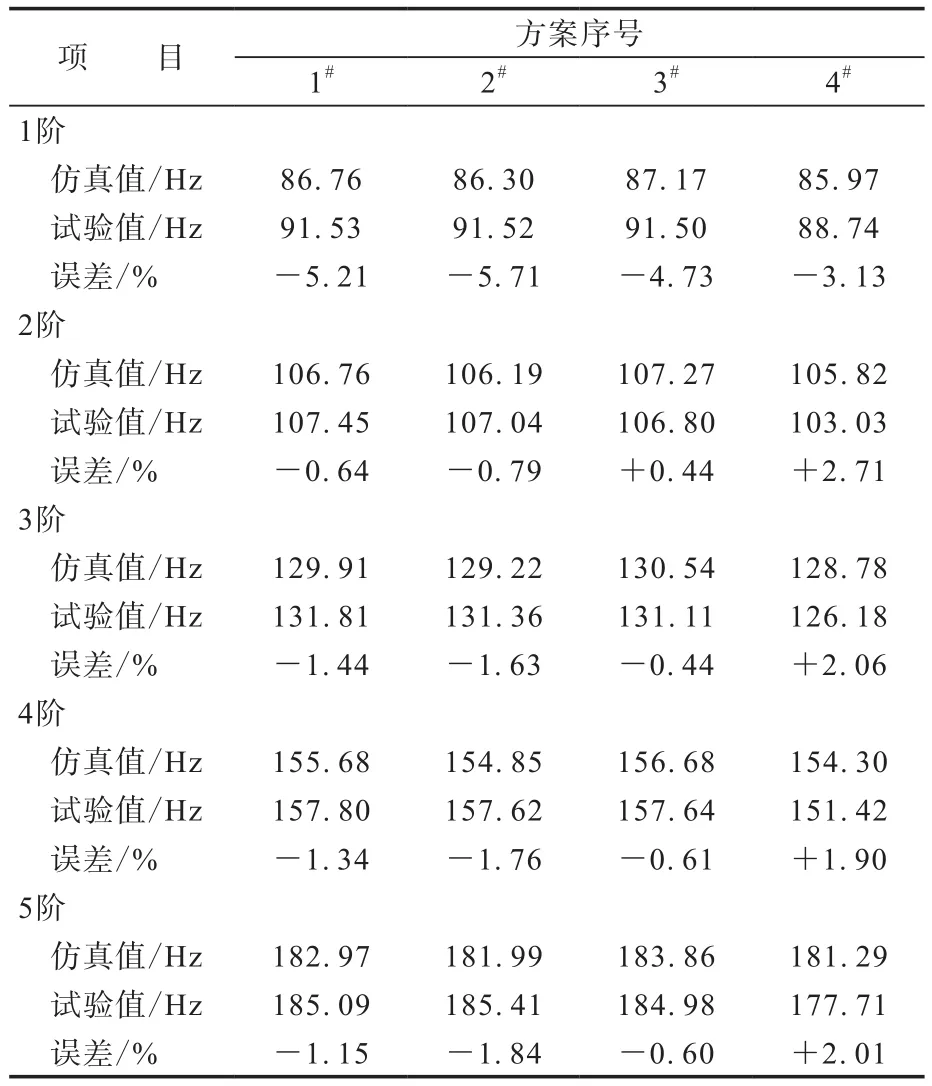
表2 不同帶束層材質(zhì)輪胎的固有頻率試驗(yàn)和仿真結(jié)果

4種材質(zhì)的仿真結(jié)果與試驗(yàn)結(jié)果趨勢(shì)基本一致，1階固有頻率計(jì)算誤差約為5%，2階以上小于4%。試驗(yàn)結(jié)果差異不明顯，但試驗(yàn)結(jié)果影響因素較多，而仿真結(jié)果受影響較小，更能反映材料對(duì)固有頻率的影響趨勢(shì)。

3.2 帶束層角度對(duì)固有頻率的影響

表3示出了3種不同帶束層角度輪胎的固有頻率模擬仿真計(jì)算結(jié)果和試驗(yàn)結(jié)果。

從表3可以看出，1階仿真結(jié)果與試驗(yàn)的誤差小于5%，2階誤差小于3%，3—5階誤差小于1.5%。

表3 不同帶束層角度輪胎的固有頻率試驗(yàn)和仿真結(jié)果

當(dāng)帶束層角度由27°變化為21°時(shí)，不同方案各階固有頻率的仿真計(jì)算值差別不大，約為1 Hz。而從試驗(yàn)結(jié)果來(lái)看，誤差均小于1 Hz，因此可以判定，帶束層角度改變對(duì)輪胎的固有頻率影響較小。

3.3 帶束層寬度對(duì)固有頻率的影響

表4示出了4種不同帶束層寬度輪胎的固有頻率的模擬仿真計(jì)算結(jié)果和試驗(yàn)結(jié)果。帶束層寬度關(guān)系為：8#＜7#＜3#＜9#。

由表4可以看出，1階仿真結(jié)果與試驗(yàn)結(jié)果誤差小于5%，2階誤差小于3%，3—5階誤差小于2%。

表4 不同帶束層寬度輪胎的固有頻率試驗(yàn)和仿真結(jié)果

每一階次下，隨著帶束層寬度的增加，固有頻率提高，最窄帶束層方案與最寬帶束層方案差異值為2～5 Hz，隨著階次增加，差異明顯。

4 固有頻率和模態(tài)測(cè)試的影響因素

4.1 輪輞材質(zhì)

針對(duì)5#方案中進(jìn)行了鍛鋁輪輞及鋼制輪輞的測(cè)試對(duì)比，對(duì)比結(jié)果見(jiàn)表5。

表5 輪輞對(duì)固有頻率測(cè)試的影響對(duì)比

由表5可以看出，輪輞對(duì)1階測(cè)試結(jié)果影響較大，鍛鋁輪輞測(cè)試結(jié)果較鋼制輪輞測(cè)試結(jié)果高約10 Hz，2—5階結(jié)果差異小于1 Hz。

4.2 輪輞約束條件

目前試驗(yàn)室內(nèi)模態(tài)測(cè)試采用的約束條件分為自由條件及固定條件兩種，本工作分別對(duì)兩種約束條件進(jìn)行對(duì)比測(cè)試，測(cè)試結(jié)果見(jiàn)表6。

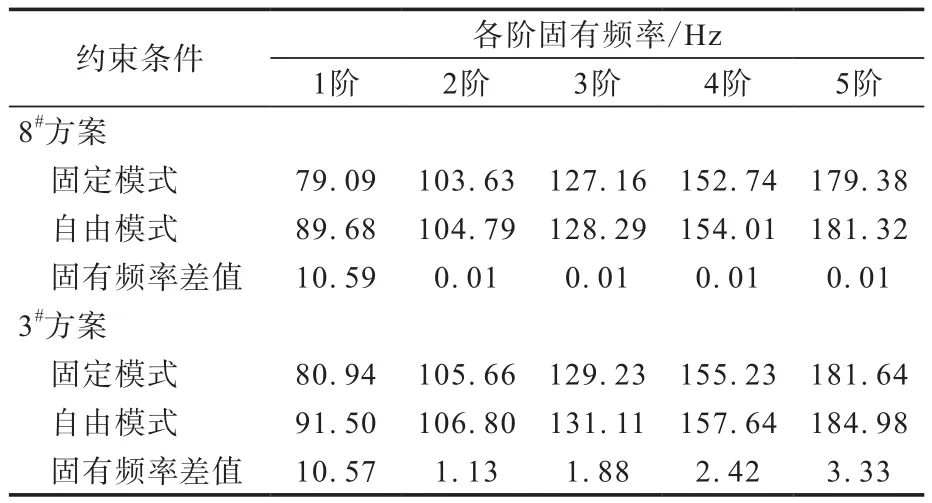
表6 約束條件對(duì)固有頻率的影響對(duì)比

由表6可以看出，自由及固定兩種約束條件主要影響1階模態(tài)固有頻率，自由狀態(tài)下的固有頻率比固定狀態(tài)下的高約10 Hz，2—5階模態(tài)比固有頻率高0～3 Hz。

5 結(jié)論

本工作開(kāi)發(fā)了輪胎固有頻率和模態(tài)的有限元仿真技術(shù)，進(jìn)行了不同帶束層結(jié)構(gòu)的多個(gè)方案固有頻率和模態(tài)的仿真計(jì)算及試驗(yàn)，結(jié)論如下。

（1）輪胎的固有頻率和模態(tài)的仿真計(jì)算結(jié)果和試驗(yàn)結(jié)果非常接近，兩者誤差小于5%，尤其是2階以上的誤差小于4%，因此有限元方法是可靠的。

（2）在21°，24°和27°范圍內(nèi)，帶束層角度對(duì)徑向振動(dòng)固有頻率影響較小。

（3）帶束層寬度和簾線種類(lèi)對(duì)固有頻率有一定影響。

（4）測(cè)試輪輞類(lèi)型和約束方式對(duì)固有頻率影響較大，對(duì)其他階的固有頻率影響不大。