諧波激勵下變壓器振動特性分析

賁彤，楊慶新，，閆榮格，祝麗花

（1.河北工業(yè)大學(xué)電磁場與電器可靠性省部共建重點(diǎn)實(shí)驗室，天津300130；2.天津工業(yè)大學(xué)電工電能新技術(shù)天津市重點(diǎn)實(shí)驗室，天津300387）

諧波激勵下變壓器振動特性分析

賁彤1，楊慶新1，2，閆榮格1，祝麗花2

（1.河北工業(yè)大學(xué)電磁場與電器可靠性省部共建重點(diǎn)實(shí)驗室，天津300130；2.天津工業(yè)大學(xué)電工電能新技術(shù)天津市重點(diǎn)實(shí)驗室，天津300387）

隨著特高壓直流輸電以及晶閘管整流設(shè)備的全面發(fā)展，電力系統(tǒng)諧波出現(xiàn)并流入變電站，使變電站中電力變壓器出現(xiàn)非正常工作狀態(tài)，影響其穩(wěn)定運(yùn)行.諧波注入使變壓器鐵心硅鋼片的磁特性包括磁化特性和磁致伸縮特性畸變，由于變壓器鐵心振動主要來源于交變磁場下硅鋼片的磁致伸縮，因此諧波下磁致伸縮特性畸變會直接導(dǎo)致變壓器振動特性異常.然而，對于這種諧波激勵下變壓器的異常振動特性，目前未見相關(guān)報道.本文在考慮磁致伸縮效應(yīng)和麥克斯韋電磁應(yīng)力的基礎(chǔ)上，研究諧波入侵對變壓器振動特性的影響.首先對疊加不同3次諧波磁場下取向硅鋼片樣片的磁化特性以及磁致伸縮特性進(jìn)行測試；然后，根據(jù)測試數(shù)據(jù)建立單相變壓器三維磁-機(jī)械耦合數(shù)值模型并進(jìn)行空載下變壓器振動仿真；根據(jù)仿真結(jié)果，分析諧波對變壓器鐵心應(yīng)力分布、振動加速度及其頻譜的影響，為分析變壓器在諧波工況下振動特性奠定理論基礎(chǔ).

諧波；磁-機(jī)械耦合數(shù)值模型；變壓器鐵心振動；變壓器鐵心應(yīng)力分布；磁致伸縮

0 引言

近年來，隨著晶閘管整流和換流技術(shù)的廣泛應(yīng)用，大量電力電子設(shè)備應(yīng)用于電力配電系統(tǒng)中，它們與用電設(shè)備一起構(gòu)成了電力系統(tǒng)諧波的主要來源.針對于電力系統(tǒng)諧波，對于大型非線性設(shè)備，如高壓直流變流器，一般采用無源濾波器進(jìn)行諧波控制，然而，由于大量分散負(fù)荷的準(zhǔn)確位置和運(yùn)行特性不能準(zhǔn)確確定，使無源濾波器對諧波的控制準(zhǔn)確性降低.目前，配電系統(tǒng)的諧波畸變水平在穩(wěn)定增長，THD（總諧波失真）的增長每年約0.1%[1]，電力系統(tǒng)諧波問題正在向日趨嚴(yán)重的方向發(fā)展.

諧波對電網(wǎng)中電力設(shè)備的影響不可忽視，它會引起電機(jī)、變壓器等電氣設(shè)備發(fā)熱，使效率降低，同時，諧波會降低繼電保護(hù)、控制，以及檢測裝置的工作精度和可靠性等[2].對于電力變壓器，當(dāng)諧波電壓施加在一次測時，鐵心硅鋼片的磁特性會產(chǎn)生畸變，包括磁化特性和磁致伸縮特性，磁化特性會影響變壓器鐵心的磁場分布，磁致伸縮特性畸變則會使硅鋼片的形變異常，影響變壓器的振動特性[3-5].目前，對于變壓器振動機(jī)理模型及特性已有相關(guān)研究，文獻(xiàn)[6-10]分析了變壓器鐵心硅鋼片的磁致伸縮特性，建立考慮磁致伸縮特性的變壓器鐵心模型并對振動噪聲進(jìn)行分析.文獻(xiàn)[11-12]根據(jù)能量變分原理，建立了變壓器磁-機(jī)械強(qiáng)耦合模型，計算了鐵心的磁場分布及振動位移.文獻(xiàn)[13-14]在建立變壓器有限元數(shù)值模型的基礎(chǔ)上，對變壓器進(jìn)行模態(tài)及頻率響應(yīng)分析.文獻(xiàn)[15]基于磁路方法建立單相變壓器振動與噪聲模型，分析了振動信號的高頻特性.文獻(xiàn)[16-17]分析了不同磁特性以及磁致伸縮特性對變壓器振動的影響，但并未分析諧波對磁特性以及變壓器振動特性的影響.文獻(xiàn)[18]建立了諧波下變壓器的非線性模型，并通過變壓器的飽和磁阻函數(shù)分析其飽和磁化狀態(tài).文獻(xiàn)[19-20]通過對變壓器鐵心模型磁致伸縮的測量，利用有限元方法，計算了變壓器二維振動模型，并分析了5次諧波對變壓器振動模態(tài)的影響，但并未考慮變壓器鐵心接縫間的麥克斯韋電磁力.因此，3次諧波下，考慮磁致伸縮力以及麥克斯韋力的變壓器振動特性（包括應(yīng)力及加速度）分析，仍未見相關(guān)報道.

首先對疊加不同3次諧波磁場下硅鋼片樣片的磁化曲線以及磁致伸縮特性曲線進(jìn)行測試；然后，根據(jù)測試數(shù)據(jù)建立單相變壓器三維磁-機(jī)械耦合數(shù)值模型并進(jìn)行空載下變壓器振動仿真；根據(jù)仿真結(jié)果，分析諧波對變壓器鐵心應(yīng)力分布、振動加速度及其頻譜的影響，為進(jìn)一步研究變壓器異常振動及降噪提供理論依據(jù).

1 磁場疊加三次諧波時硅鋼片磁化特性和磁致伸縮特性測試

在我國低壓配電網(wǎng)中，諧波主要以3次諧波為主，3次諧波電流在零線上疊加，造成零線電流過大，嚴(yán)重時發(fā)生燒斷和火災(zāi)，我國每年都有因3次諧波造成的故障和事故[19]，因此本文主要研究3次諧波對變壓器振動的影響.

本文首先利用激光磁致伸縮及磁化特性測量系統(tǒng)，對組成變壓器鐵心的取向硅鋼片進(jìn)行磁化特性及磁致伸縮特性測試，測試系統(tǒng)如圖1所示，該系統(tǒng)符合IEC標(biāo)準(zhǔn)[20].工作原理為：激光器（工作頻率為50 Hz，分辨率為10 nm/m）發(fā)射光束到反光片，反光片貼在測試樣片可以自由伸縮的一端，樣片另一端固定，且在樣片長度方向施加磁場，此時樣片產(chǎn)生磁致伸縮，反光片將光束反射回激光器，根據(jù)反射時間差得到檢測樣片的磁致伸縮形變量；同時，根據(jù)不同激勵條件下，不同磁通密度幅值下磁滯回線頂點(diǎn)連線得到樣片在不同激勵條件下的磁化曲線.

測量中，3次諧波以不同含量疊加在取向硅鋼片樣件的基波磁場上，合成磁場可表示為，

其中：B1為磁通密度基波分量幅值；n為疊加的3次諧波幅值相對于基波幅值的比例；ω為角頻率，ω= 2πf，f=50 Hz；θ為3次諧波滯后于基波的相位角.

針對疊加諧波激勵下硅鋼片磁化特性以及磁致伸縮特性，對組成變壓器鐵心的取向硅鋼片，進(jìn)行了不同含量，不同相位角諧波疊加的多組測試，并建立數(shù)據(jù)庫.取n=50%，θ=0°時不同磁通密度幅值下磁致伸縮量隨時間變化曲線及頻譜進(jìn)行分析，如圖2所示.

圖1 磁化及磁致伸縮特性測量系統(tǒng)Fig.1 Magnetization and magnetostrictive characteristic measurement system

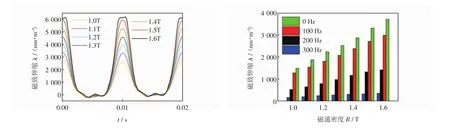
圖2 當(dāng)疊加的3次諧波n=50%θ=0°時，不同磁通密度幅值下硅鋼片磁致伸縮曲線及頻譜Fig.2 Magnetostrictive curves of silicon steel sheet when the third harmonic parameters are n=50%θ=0°under different magnetic flux density values

在磁場作用下，鐵磁材料晶體的磁疇壁移動并旋轉(zhuǎn)，宏觀上表現(xiàn)為材料產(chǎn)生磁致伸縮形變，由圖2a）可以看出，對硅鋼片樣片長度方向施加正弦交變磁場時，隨著磁場的增大，磁致伸縮量不斷增大，周期為0.01s，即激勵磁場周期的一半；由圖2b）可以看出，磁致伸縮曲線的頻率主要分布在0Hz、100Hz、200 Hz、300 Hz，其中300 Hz所占的比例較小，隨著磁通密度幅值的增加，100 Hz磁致伸縮幅值所占的比例增加.

母親在我面前替父親說好話。母親說起那年那場大雪，父親原是準(zhǔn)備坐輪船去上海的，卻得到我患病的口信，連夜往家趕。路上用他最鐘愛的口琴換了兩只橘子帶給我。大雪漫天，沒有可搭乘的車輛，他就一路跑著。過了江，好不容易攔下一輛裝煤的卡車……

為分析不同含量，不同相位角諧波疊加對硅鋼片磁致伸縮特性的影響，對不同磁通密度幅值下硅鋼片磁致伸縮λ與磁通密度B的關(guān)系曲線進(jìn)行分析，選取n=0，θ=0°、n=25%，θ=0°、n=25%，θ=90°、n= 50%，θ=0°、θ=50%，θ=90°五組激勵進(jìn)行研究，磁致伸縮特性曲線如圖3所示.

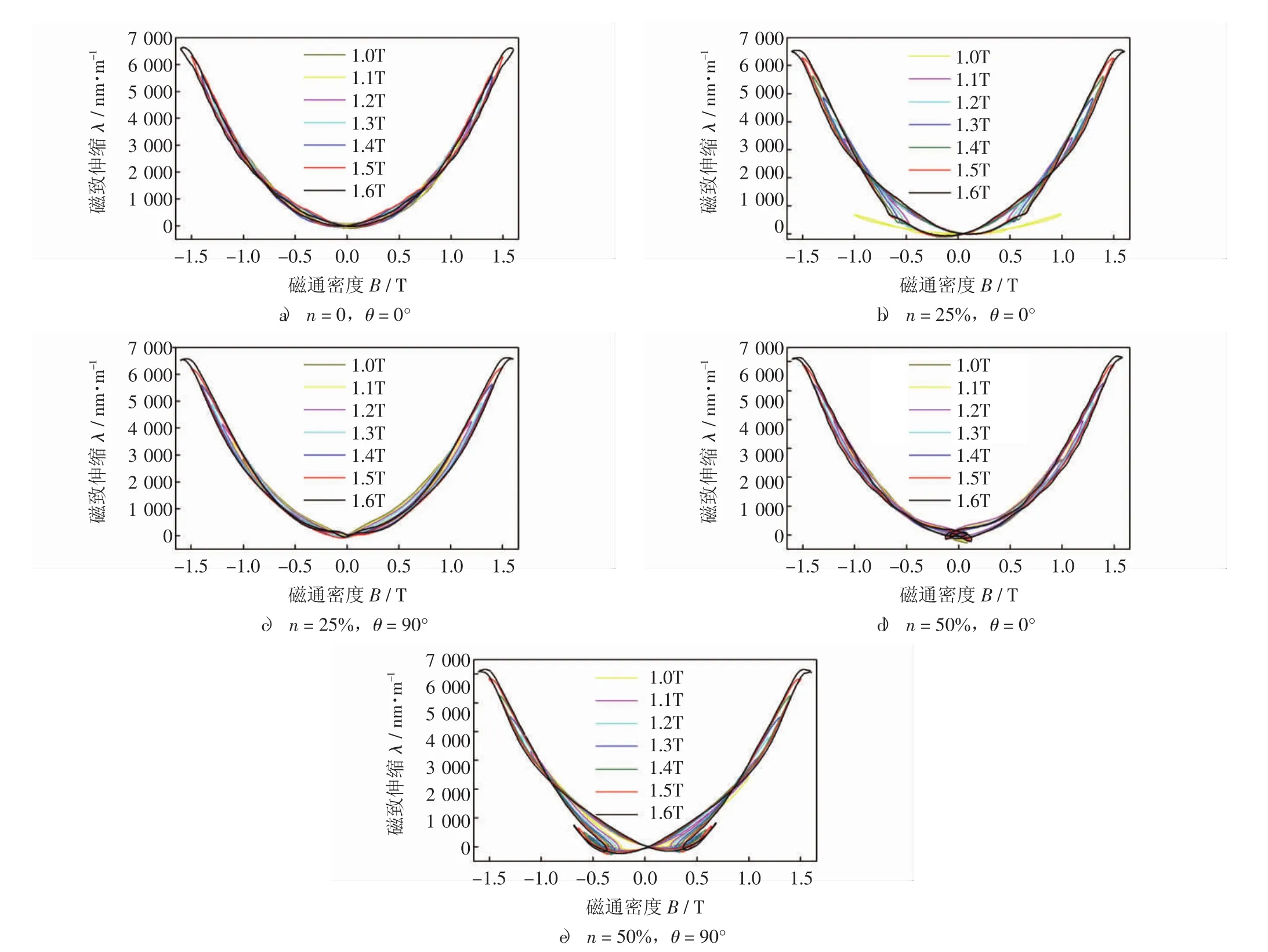
圖3 疊加不同3次諧波時，不同磁通密度幅值下硅鋼片磁致伸縮回環(huán)Fig.3 Magnetostriction loops under different magnetic flux density values and the third harmonic parameters

從圖3可以看出，諧波的疊加對磁致伸縮回環(huán)的面積無影響，當(dāng)磁通密度幅值Bmax=1.6T時，圖3b）-圖3e）中磁致伸縮回環(huán)出現(xiàn)畸變，磁致伸縮形變增量開始保持不變，即達(dá)到飽和，圖3a）中磁致伸縮回環(huán)則未出現(xiàn)上述畸變，這說明諧波的注入使硅鋼片磁致伸縮更容易達(dá)到飽和；且當(dāng)諧波的含量較大時，相位角θ越大，磁致伸縮回環(huán)在零點(diǎn)附近的畸變越嚴(yán)重.因此，諧波的疊加降低了硅鋼片的耐飽和能力并引起磁致伸縮曲線回環(huán)畸變.

諧波的疊加會使硅鋼片磁滯回線出現(xiàn)波形畸變，疊加的諧波含量以及相位角不同，磁滯回線會出現(xiàn)不同程度的小回環(huán)[20]，如圖4a）所示，目前，對于這種畸變曲線如何使用，尚無可行的定義方法，將不同磁通密度幅值下磁滯回線頂點(diǎn)連線，得到基本磁化曲線，如圖4b）所示，由圖4b）可以看出，不同激勵下基本磁化曲線基本重合.根據(jù)上述測量結(jié)果磁致伸縮特性曲線λ（B）和磁化曲線H=ν（B），可插值得到磁致伸縮系數(shù)d和磁阻率ν，并應(yīng)用于變壓器振動數(shù)值分析模型.

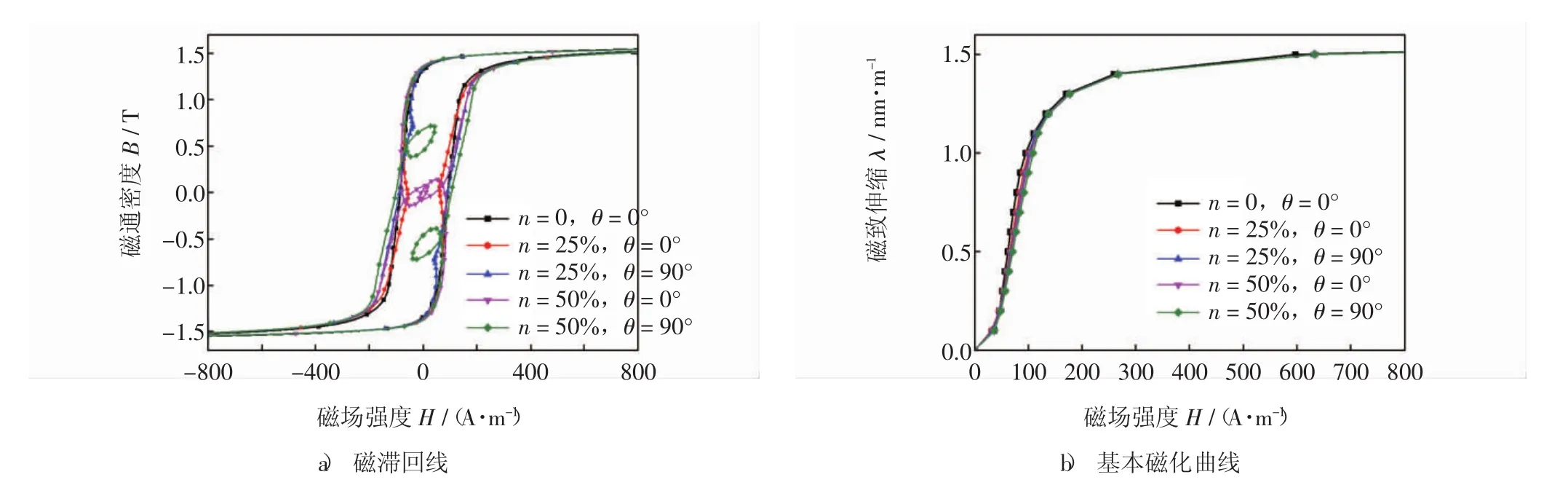
圖4 疊加不同3次諧波時硅鋼片磁化特性曲線Fig.4 Magnetization curves of silicon steel sheet under different the third harmonic parameters

2 變壓器振動數(shù)值分析模型

本文利用有限元進(jìn)行計算時，利用電磁場和機(jī)械場的能量泛函來離散求解電磁場和機(jī)械場的剛度矩陣，變壓器的電磁-機(jī)械系統(tǒng)的總能量包括磁場能、應(yīng)變能、電流位能、磁致伸縮能、麥克斯韋電磁應(yīng)力所做的功.則系統(tǒng)的能量泛函為

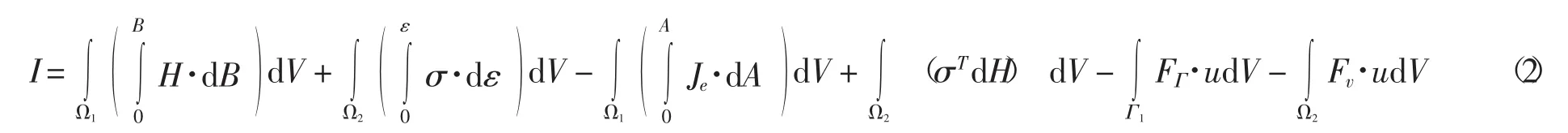
式中：Ω1，Ω2分別表示電磁場和機(jī)械場的分析域；Γ1為機(jī)械場的邊界；A為磁場矢量；u為變壓器鐵心振動位移；σ、ε分別為應(yīng)力和應(yīng)變；FΓ和Fv分別為變壓器鐵心受外部體積力和鐵心表面受到的邊界面力；d為磁致伸縮系數(shù)，可由已測得的磁致伸縮特性曲線λ（B）插值得到；磁場強(qiáng)度H和磁通密度B的關(guān)系為：H=νB，其中ν為磁阻率，可由測量的磁化曲線插值計算得到；Je為外部電流密度，可由不同含量3次諧波電壓下實(shí)測勵磁電流i1（t）、i2（t）、i3（t）得到，即

式中，s為線圈導(dǎo)線截面積.

將能量泛函按直角坐標(biāo)系展開，即

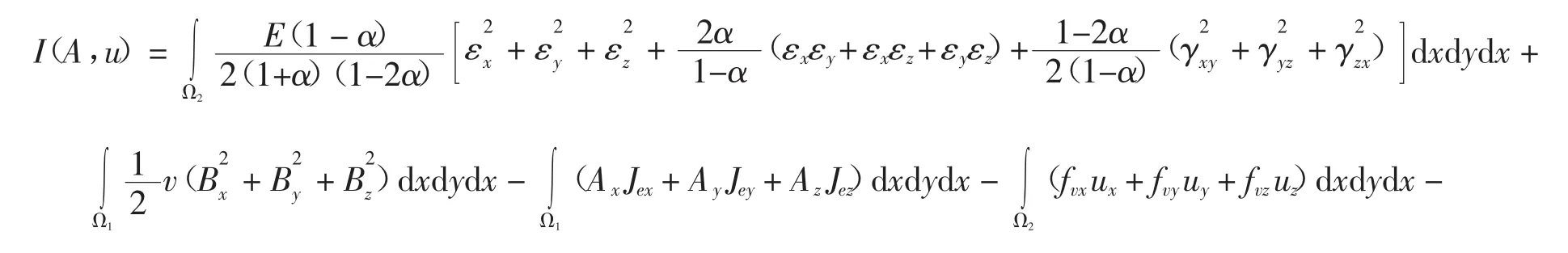
其中：E為楊氏模量；α為泊松比；εx，εx，εx為正應(yīng)變，γxy，γxy，γxy為剪應(yīng)變.

能量泛函，即公式（4），磁場矢量A和位移矢量u的泛函，對能量泛函做單元離散化處理并取極值，得到有限元方程組

表達(dá)式為

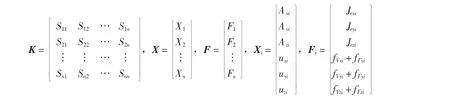
變壓器鐵心振動加速度a為

3 疊加諧波激勵下變壓器鐵心振動數(shù)值計算及結(jié)果分析

以單相干式電力變壓器為仿真對象，基于上述電磁-機(jī)械耦合模型，利用有限元數(shù)值方法進(jìn)行仿真.仿真中，3次諧波以不同含量疊加在變壓器1次側(cè)電壓中，1次側(cè)電壓u（t）可表示為如下形式

其中：U1為電壓基波分量；n為疊加的3次諧波幅值占基波幅值的比例；ω為角頻率，ω=2πf，f=50 Hz；θ為3次諧波滯后于基波的相位角.

為研究變壓器1次側(cè)電壓疊加諧波時的空載振動特性，本文對變壓器鐵心接縫處進(jìn)行應(yīng)力分析，并取變壓器鐵心上端部一點(diǎn)，分析其豎直方向的振動加速度，采樣點(diǎn)以及采樣接縫分布如圖5所示.疊加不同3次諧波電壓時，該處的應(yīng)力分布如圖6所示，振動加速度曲線及頻譜分別如圖7所示.

由圖6可以看出，變壓器鐵心接縫處的應(yīng)力主要分布在邊緣，隨著諧波的疊加，鐵心內(nèi)部拐角處的應(yīng)力逐漸增大，偏離拐角應(yīng)力減小，這是由于諧波的疊加使硅鋼片磁致伸縮特性曲線易于飽和；同時，隨著諧波含量的增加，接縫處應(yīng)力的幅值逐漸增大，隨著諧波滯后于基波相位角的增加，應(yīng)力分布的不均勻性加劇.

圖7中，諧波的疊加加劇了變壓器鐵心的振動，隨著諧波含量的增加，振動幅值加大，而圖3中磁致伸縮量隨著諧波的疊加卻逐漸變小，這是由于3次諧波的注入使鐵心耐飽和能力降低，即諧波的疊加使鐵心較易飽和，從而使振動幅值變大；隨著3次諧波含量的增加，200 Hz、300 Hz上加速度的幅值增大，即3次諧波的含量及相位角影響了振動加速度的頻率分布.

諧波的疊加引起了磁致伸縮特性畸變，這導(dǎo)致變壓器鐵芯振動加劇，但同時，諧波的疊加也使變壓器1次側(cè)激勵電壓有效值增大，這也是振動加劇的一個原因.為分析振動的強(qiáng)弱是由諧波引起的，

圖5 變壓器鐵心上振動加速度采樣點(diǎn)及采樣接縫位置Fig.5 Vibration acceleration sampling point and sampling joint location on transformer core

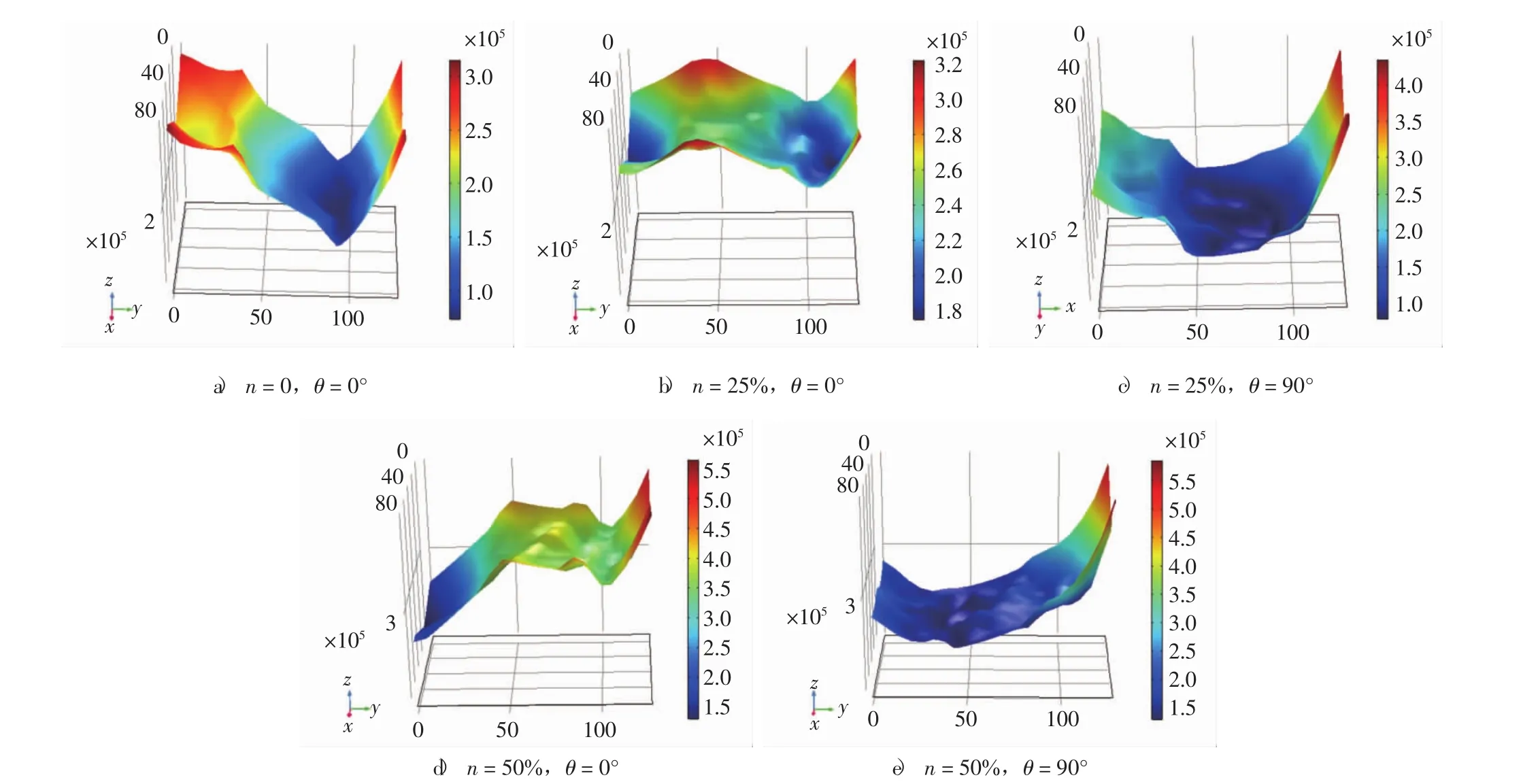
圖6 疊加不同諧波電壓時，變壓器鐵心接縫處應(yīng)力分布（單位：N/m2）Fig.6 Transformer core stress distribution at silicon steel sheet joint when excitation source are superposed with different the third harmonic voltages

圖7 疊加不同諧波電壓時，變壓器鐵心豎直方向振動加速度曲線及頻譜Fig.7 Transformer core vibration acceleration curves and frequency spectrum at vertical direction when excitation source are superposed with different the third harmonic voltages

還是電壓有效值增大后磁致伸縮強(qiáng)度增大引起的，或者兩者兼有，本文針對n=50%，θ=90°的情況，作了一個對比仿真，令電壓有效值相同，u1（t）可表示為

其中：U1為變壓器1次側(cè)基波電壓幅值；ω為角頻率，ω=2πf，f=50 Hz.取圖5所示的采樣點(diǎn)，得到兩組仿真結(jié)果的加速度及其頻譜對比，如圖8所示.

由圖8可以看出，當(dāng)電壓有效值相同時，疊加諧波與不疊加諧波的變壓器鐵心豎直方向振動加速度幅值變化明顯，疊加諧波時振動加速度幅值明顯高于無諧波情況，且諧波的疊加使振動加速度曲線波形畸變，在200 Hz和300 Hz上加速度幅值增大，即加速度產(chǎn)生2次、3次諧波，這說明勵磁電壓有效值增大對于變壓器振動的影響遠(yuǎn)弱于疊加諧波本身對變壓器振動的影響.因此，當(dāng)諧波疊加在變壓器激勵電壓中時，由于諧波的注入變壓器振動加劇；同時，疊加諧波一定程度上使變壓器鐵心激勵電壓有效值增大，但這不是諧波影響變壓器振動的主要原因，變壓器振動加劇以及波形畸變主要是由于諧波的疊加使鐵心材料磁特性曲線飽和工作點(diǎn)降低引起的.

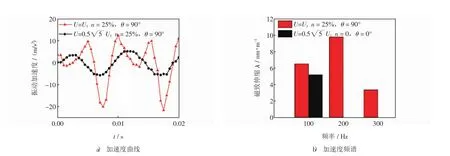
圖8 電壓有效值相同時，疊加諧波與不疊加諧波的變壓器鐵心豎直方向振動加速度曲線及頻譜Fig.8 Transformer core vibration acceleration curves and frequency spectrum at vertical direction with different excitation sources

4 結(jié)論

本文在考慮磁致伸縮應(yīng)力和麥克斯韋應(yīng)力的基礎(chǔ)上，研究了3次諧波對變壓器振動特性的影響，以實(shí)驗測量的變壓器鐵心硅鋼片磁化曲線及磁致伸縮特性曲線為基礎(chǔ)，建立變壓器三維電磁-機(jī)械耦合數(shù)值模型并進(jìn)行空載振動仿真，研究結(jié)果表明：諧波的含量以及其滯后于基波相位角的不同，影響了變壓器鐵心材料的耐飽和能力，從而使變壓器振動加劇且振動波形畸變；隨著諧波含量以及其滯后于基波相位角的增大，變壓器鐵心應(yīng)力出現(xiàn)分布不均現(xiàn)象，鐵心內(nèi)部接縫處應(yīng)力增加，總體上加劇了變壓器鐵心的振動，同時也影響了振動加速度的頻率分布，出現(xiàn)2次、3次諧波.

[1]阿里拉加，沃森.電力系統(tǒng)諧波[M].第2版.北京：中國電力出版社，2008.

[2]郎維川.供電系統(tǒng)諧波的產(chǎn)生，危害及其防護(hù)對策[J].高電壓技術(shù)，2002，28（6）：30-31.

[3]鐘文定.鐵磁學(xué)（中冊）[M].北京：科學(xué)出版牡，1987.

[4]Moses A J，Anderson P I，Phophongviwat T，et al.Contribution of magnetostriction to transformer noise[C]//Universities Power Engineering Conference. IEEE，2010：1-5.

[5]Moses A J.Effects of magnetic properties and geometry on flux harmonics and losses in 3-phase，5-limb，split-limb，transformer cores[J].IEEE Trans. Magn.，1987，23（5）：3780-3782.

[6]Belahcen A，Singh D，Rasilo P，et al.Anisotropic and strain-dependent model of magnetostriction in electrical steel sheets[J].IEEE Trans Magn，2015，51（3）：1-4.

[7]Pfutzner H，Shilyashki G，Hamberger P，Aigner M，et al.Automatic 3-D building factor analyses of a grain-oriented model transformer core[J].IEEE Trans Magn，2014，50（4）：8400604.

[8]Zhang Y L，Wang J Y，Sun X G，et al.Measurement and modeling of anisotropic magnetostriction characteristic of grain-oriented silicon steel sheet under DC bias[J].IEEE Trans Magn，2014，50（2）：1-4.

[9]Shilashki G，Pfutzner H，Hofbauer F，et al.Magnetostriction distribution in a model transformer core[J].J Electr Eng，2010，61（7）：130-132.

[10]Weiser B，Pfützner H，Anger J.Relevance of magnetostriction and forces for the generation of audible noise of transformer cores[J].IEEE Trans Magn，2000，36（5）：3759-3776.

[11]祝麗花，楊慶新，閆榮格，等.考慮磁致伸縮效應(yīng)電力變壓器振動噪聲的研究[J].電工技術(shù)學(xué)報，2013，25（4）：1-6+19.

[12]Zhu L H，Yang Q X，Yan R G，et al.Numerical computation for a new way to reduce vibration and noise due to magnetostriction and magnetic forces of transformer cores[J].J Appl Phys，2013，113（17）：468.

[13]Wiak S，Witczak P，Kubiak W.Vibration analysis of small power transformer[J].COMPEL，2010，29（4）：1116-1124.

[14]Kitagawa W，Ishihara Y，Todaka T，et al.Analysis of structural deformation and vibration of a transformer core by using magnetic property of mangnetostriction[J].Electr Eng Jpn，2010，172（1）：19-26.

[15]Hsu C H，Liu C H，Hsiao Y C，et al.High frequency characteristics of magnetostriction on vibration and noise for single-phase transformer dependence of magnetic circuit method[C]//2014 International Symposium on Computer Consumer and Control（IS3C），2014.

[16]Zhuikov V，Kuznietsov N.Modeling of electrical and vibration signals of transformers with different magnetic properties[C]//IEEE Electronics and Nanotechnology（ELNANO），2013：373-377.

[17]Li Q，Wang X，Zhang L，et al.Modelling methodology for transformer core vibrations based on the magnetostrictive properties[J].IET Electr Power Appl，2012，6（9）：604-610.

[18]Pedra J，Corcoles F，Sainz L，et al.Harmonic nonlinear transformer modeling[J].IEEE Trans Power Delivery，2004，19（2）：884-890.

[19]Ghalamestani S G，Vandevelde L，Dirckx J J J，et al.Magnetostriction and the influence of higher harmonics in the magnetic field[J].IEEE Transactions on Magnetics，2012，48（11）：3981-3984.

[20]Ghalamestani S G，Vandevelde L，Dirckx J J J，et al.Magnetostrictive vibrations model of a three-phase transformer core and the contribution of the fifth harmonic in the grid voltage[J].Journal of Applied Physics，2014，115（17）：17A316-1-3.

[21]龍虎.零線電流過大致電氣火災(zāi)的防治[J].消防技術(shù)與產(chǎn)品信息，2013，3（1）：9-11.

[22]Electrical Steel—Methods of measurement of the magnetostriction characteristics by means of single sheet and epstein test specimens，Standard IEC/ TR 62581，2010.

[23]程志光，高橋則雄，博扎徳·弗甘尼.電氣工程電磁熱場模擬與應(yīng)用[M].北京：科學(xué)出版社，2009.

[責(zé)任編輯 代俊秋]

On influence of harmonic excitationon the transformer vibration

BEN Tong1，YANG Qingxin1，2，YAN Rongge1，ZHU Lihua2

（1.Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability,Hebei University of Technology,Tianjin,300130,China;2.Tianjin Key Laboratory of Advanced Technology of Electrical Engineering and Energy, Tianjin Polytechnic University,Tianjin 300387,China）

With development of the ultra-high voltage DC transmission system and the thyristor rectifier equipment in high voltage distribution network,theharmonic in power system is injected into transformer substation,which will lead to the abnormal operating of transformer.Transformer core is assembled by silicon-steel lamination.The silicon steel produces regular deformation due to the magnetostriction effect in an alternating magnetic field.Meanwhile,the magnetic and magnetostrictive characteristics of silicon steel will distort when harmonic voltages are applied to the transformer windings, which will influence the transformer vibration.However,the vibration characteristic of transformer under harmonic excitation has not been reported.This paper studies the influence of harmonic on the transformer vibration by considering Maxwell electromagnetic force and magnetostriction effect.Firstly,magnetic and magnetostrictive characteristic curves are tested when excitation magnetic source is superposed with different the third harmonics.Then,a three-dimensional magneto-mechanical coupled model of transformer is presented.The influence of the third harmonic on core stress distribution, vibration acceleration curves and frequency spectrum are analyzed,which can help lay the theoretical basis on the study of transformer vibration under different harmonic excitations.

harmonic;magneto-mechanical strongly coupled model;transformer core vibration;stress distribution of transformer core;magnetostriction

TM412

A

1007-2373（2017）03-0001-08

10.14081/j.cnki.hgdxb.2017.03.001

2017-02-18

國家自然科學(xué)基金重點(diǎn)項目（51237005）；國家自然科學(xué)基金（51507110，51177038）.

賁彤（1991-），女，博士研究生.