基于Gumbel Copula的高可靠性結構系統分析

吳金華，何軍

（上海交通大學船舶海洋與建筑工程學院，上海200240）

基于Gumbel Copula的高可靠性結構系統分析

吳金華，何軍

（上海交通大學船舶海洋與建筑工程學院，上海200240）

提出了一種基于Gumbel Copula的高可靠性結構系統失效概率計算方法.該方法采用移位廣義對數正態分布（SGLD）來估計結構反應的邊緣分布，采用Copula函數來估計系統反應的聯合分布函數，而Copula函數的參數估計采用矩方法.采用本文發展的方法，分析了地震作用下六層鋼框架結構系統的可靠度，結果表明該方法不僅可以給出精確的結構反應邊緣分布和聯合分布表達式，而且具有較高的數值精度和計算效率.

Copula函數；系統可靠度；移位廣義對數正態分布；概率分布；參數估計

結構系統可靠度分析是結構安全評估及設計的基礎，高可靠性問題是可靠度分析中的核心問題.針對這一問題的研究，人們已經發展出了多種方法，包括一次二階矩方法、二次二階矩方法、稀疏網格法、響應面法以及神經網絡法等[1-6].這些方法適用于處理低維度的可靠度問題，對于高維結構系統的可靠度，其精度和效率均無法達到工程要求.目前，常用的系統可靠度分析方法主要有數值模擬方法和邊界法.數值模擬方法包含蒙特卡洛方法、重要抽樣法[7]、子集模擬法[8-9]、線抽樣法[10]、方向抽樣法[11]等.這些方法的計算精度需要通過抽樣次數來保證，對于高可靠性問題，其效率低下.邊界法主要包含二階窄邊界法[12]、三階窄邊界法[13]、線性規劃邊界法[14]等，此3種方法由于各自應用范圍和效率的缺陷，均無法滿足高可靠性結構系統的分析要求.

基于以上現狀，對于高可靠性結構系統可靠度分析還缺少非常有效的方法.本文提出了一種基于Gumbel Copula模型的系統可靠度分析方法，該方法采用SGLD模型估計結構反應的邊緣分布，采用矩方法估計Copula模型的參數.一個6層鋼框架結構系統的地震響應分析說明了本文所建立方法的有效性和精確性.

1 Copula函數及其模型建立

Copula由Sklar[15]提出，是一種將多維隨機變量的聯合分布用其一維邊緣分布表示的函數.Copula函數最早被應用于金融分析領域，近年來逐漸被應用于結構可靠度和工程抗震、氣象和水文、統計和環境等諸多領域.多元Copula函數的定義如下：

定義1n維Copula是定義域為[0，1]n，值域為[0，1]的函數，即C[0，1]n→[0，1]，且滿足下列條件：

1）對任意u∈[0，1]n，如果存在某個分量uk=0（k=1，2，…，n），則C（u）=0；

2）對任意u∈[0，1]n，如果存在u1=…=uk-1=uk+1=un=1，則C（u）=1；

3）對于定義域[0，1]n中的任意2個向量，令

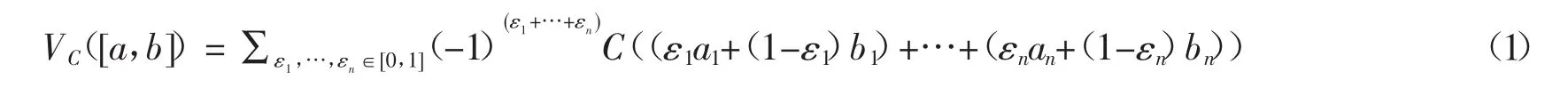
如果a≤b，那么VC（[a，b]）≥0.其中VC（[a，b]）稱為[a，b]的C容積.

定義2（n維Sklar定理）[15]設H是邊緣分布為u1，u2，…，un的n維聯合分布函數，那么一定存在一個Copula函數C，對于任意的x∈Rn，有

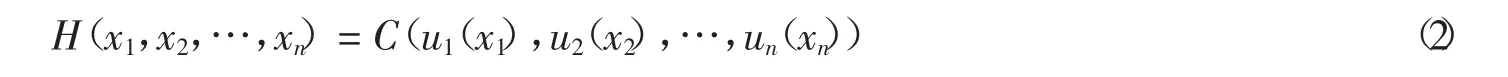
如果u1，u2，…，un是連續的，那么C是唯一的；否則，C在Ran（u1）×…×Ran（un）上是唯一的.反之，如果u1，u2，…，un是分布函數，則C（u1（x1），u2（x2），…，un（xn））是一個聯合分布，且其邊緣分布為u1，u2，…，un.

構造Copula函數有很多方法，包含幾何方法、代數方法、用Archimedean族[15]的生成元構造等.其中單一參數的Archimedean Copula函數構造簡單，適用性強且具有較好的性質，是工程結構可靠度分析中非常適用的方法，尤其是Gumbel Copula對串聯系統具有較好的適用性[16].

Gumbel Copula的表達式如下：

式中：ui，i=1，2，…，n表示結構反應的邊緣分布函數；θ是Gumbel Copula的模型參數.

由式（3）可知，Copula函數的建模包含2個過程，即邊緣分布模型的建立和Copula函數的參數估計.下面詳細介紹這2個過程.

2 Copula函數的邊緣分布建模及參數估計

2.1 Copula函數的邊緣分布建模

由于移位對數正態分布模型可以用來考慮不同的偏態系數的函數，指數冪分布模型可以用來考慮不同的峰度系數的函數，通過結合移位對數正態分布模型和指數冪分布模型可以得到廣義移位對數正態分布（SGLD）模型，該模型可以考慮廣闊的偏態-峰度系數空間，進而模擬各種不同的函數類型[17].

本文采用SGLD模型來估計結構系統反應的邊緣分布，其PDF表達式如下：

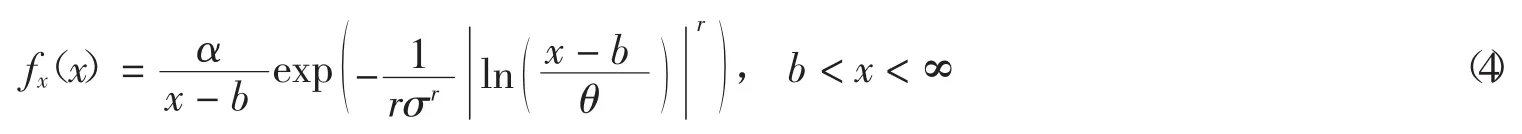
其中：σ、r為型參數；b為位置參數；θ為尺寸參數.

廣義對數正態分布的CDF表達式如下：

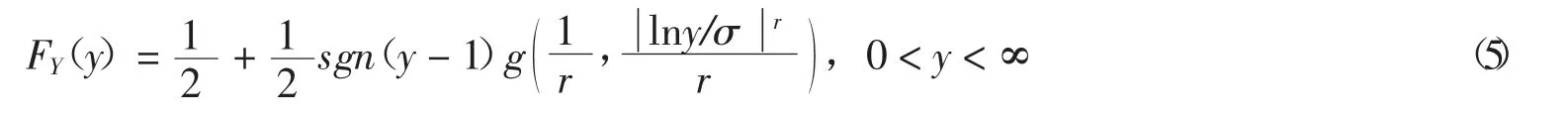
2.2 SGLD模型的參數估計

SGLD模型的參數估計常采用矩方法，該方法具有較高的精度，應用廣泛.SGLD的CDF表達式中Y的均值μy、方差偏態系數γy和峰度系數κy可以通過其原始矩E[Yk]求得.

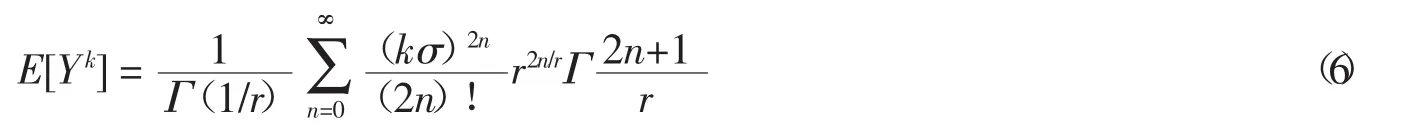
這里，σ、r為未知的模型參數.由于偏態系數γy和κy峰度系數都是型參數σ、r的函數，且Y=（X-b）/θ的變量變換并不改變偏態系數峰度系數的數值，因此可以得到如下關系式：

該關系式可以表達如下：

其中，μ為未知向量[σ、r]T.由于γX和κX可通過對隨機變量的樣本進行統計得到，通過求解式（9）可以得到未知變量σ、r.

在σ、r已知的情況下，通過如下關系式可以求解θ、b：

這里，μY和σY可以由型參數σ、r代入式（6）求得；μX和σX可以通過對隨機變量進行樣本統計得到.下面主要問題是求解μ.

為求得向量μ，用牛頓迭代方法求解式（9），迭代公式：

其中

3 Copula函數的參數估計

Gumbel Copula是一種工程中常用的Copula函數，對于本文采用的單一參數多變量Gumbel Copula，主要需要估計其參數.由文獻[18]可知，矩方法對阿基米德型Copula的參數估計具有較好的適用性，矩方法的基本思想是對于已知的充足樣本數，讓基于樣本的Kendell’s tau與基于總體的Kendell’s tau相等，進而通過等式計算求解出Copula參數.相比于傳統的最大似然法，基于Kendell’s tau的參數估計方法更簡單和靈活，具有更高的效率，對于單參數阿基米德型Copula具有很好的適用性[16].本文中阿基米德型Copula參數估計所需樣本可由用于SGLD模型估計參數時的反應樣本得到.

對于n維Gumbel Copula Cθ（u），u=（u1，u2，…，un），其樣本一致性系數Kendell’s tau的計算公式為[79]：

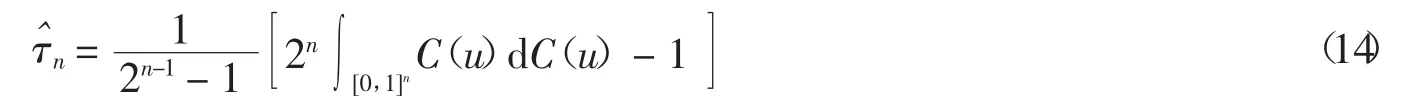
若樣本數N已知，該公式可以簡化如下：

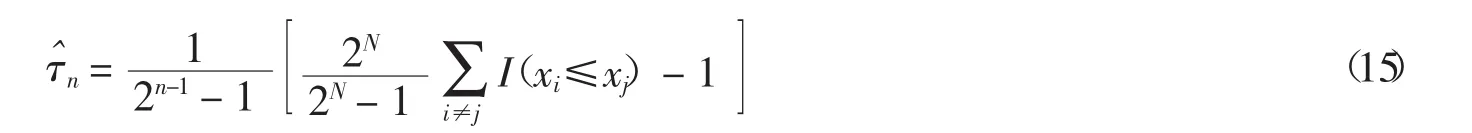
對于n維Gumbel Copula C（θu），u=（u1，u2，…，un），其總體的Kendell’s tau在n維串聯系統模型中的計算公式如下：

4 基于Copula函數串聯結構系統的聯合失效概率

對于n維串聯結構系統[19]，系統中任意一個元件的失效均會導致整個系統失效，其失效概率的計算公式如下：

式中：xi表示串聯結構系統中第i個元件的反應值；δi表示第i個元件反應的極限值.由Copula函數的定義[15]可知，上式可用Copula函數表述如下：

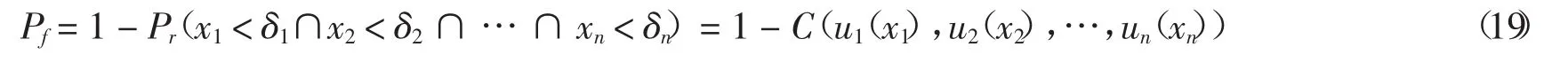
5 算例研究

為了檢驗本文所提出方法的計算精度和效率，本算例考慮一個如圖1所示的遭受水平方向地震作用的6層抗彎鋼框架.結構構件的截面形式如表1所示，各樓層的水平地震荷載如圖1所示.假設水平地震荷載為相互獨立的對數正態分布隨機變量，其均值從頂部的750 kN線性變化到底部的0，而變異系數均為δF= 0.2.假設所有構件的彈性模型E為對數正態分布隨機變量，均值μE=200 kN/mm2，變異系數δE=0.1.在本例中，7個基本輸入隨機變量分別為水平地震荷載F1，…，F6及彈性模量E.構件的失效概率定義為相應框架柱層間位移比θ大于層間位移比限值θC的概率，構件的功能函數為：

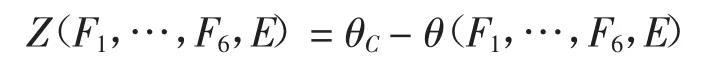
其中的θ（F1，…，F6，E）代表構件的層間位移比.對于該串聯結構體系，假設任意一個框架柱失效結構就失效，則結構失效概率可表示為

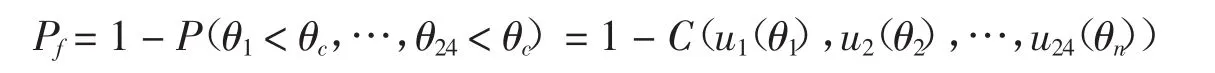
其中的θi，i=1，2，…，24代表第i根框架柱的層間位移比.

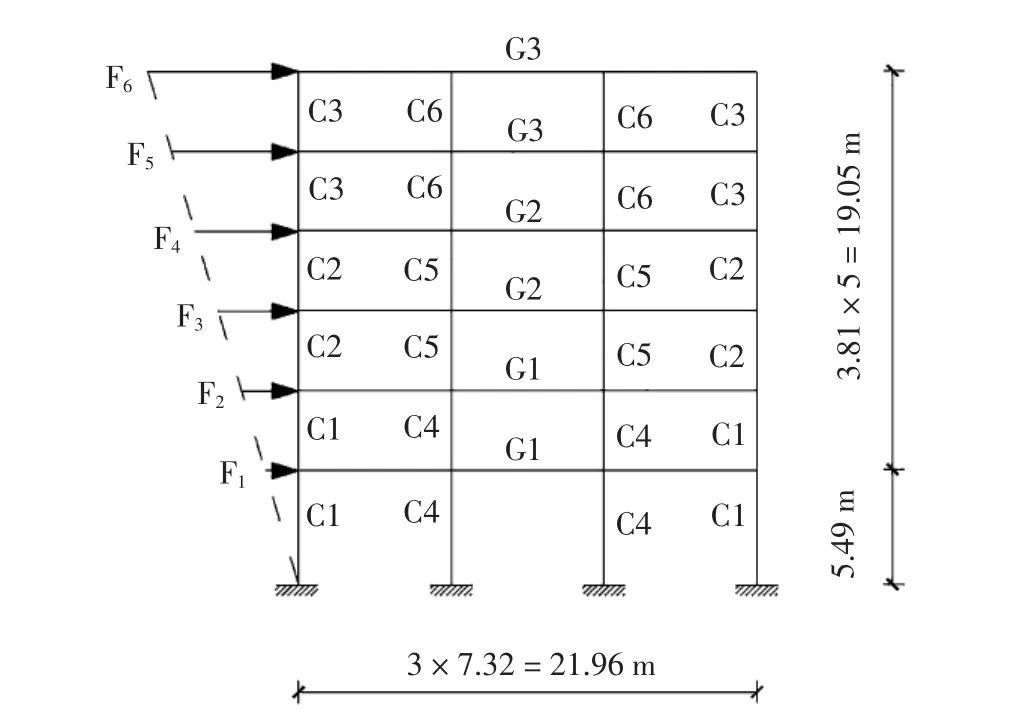
圖1 六層鋼框架結構分析模型Fig.1 A six-story steel-frame structure model

由基于3 000個樣本的矩方法可以估計出結構反應邊緣分布的SGLD模型尾部分布的近似值.圖2繪出了由反應X5和X6的尾部分布（SGLD）以及由基于30 000個樣本由Monte Carlo方法得到的尾部分布值.圖2表明：在X5和X6分布的中段，由矩方法得到的SGLD給出的超越概率與Monte Carlo結果幾乎一致，而在X5和X6分布的尾部，基于30 000個樣本的Monte Carlo方法不能給出相應的超越概率，但由矩方法得到的SGLD可以給出相當合理的結果.因此，基于矩方法的SGLD模型是可用于本結構反應分布的尾部估計的.

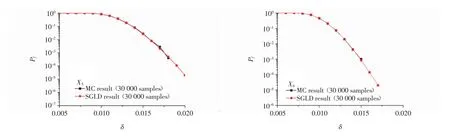
圖2 反應X5和X6的尾部分布Fig.2Tail distributions of X5and X6

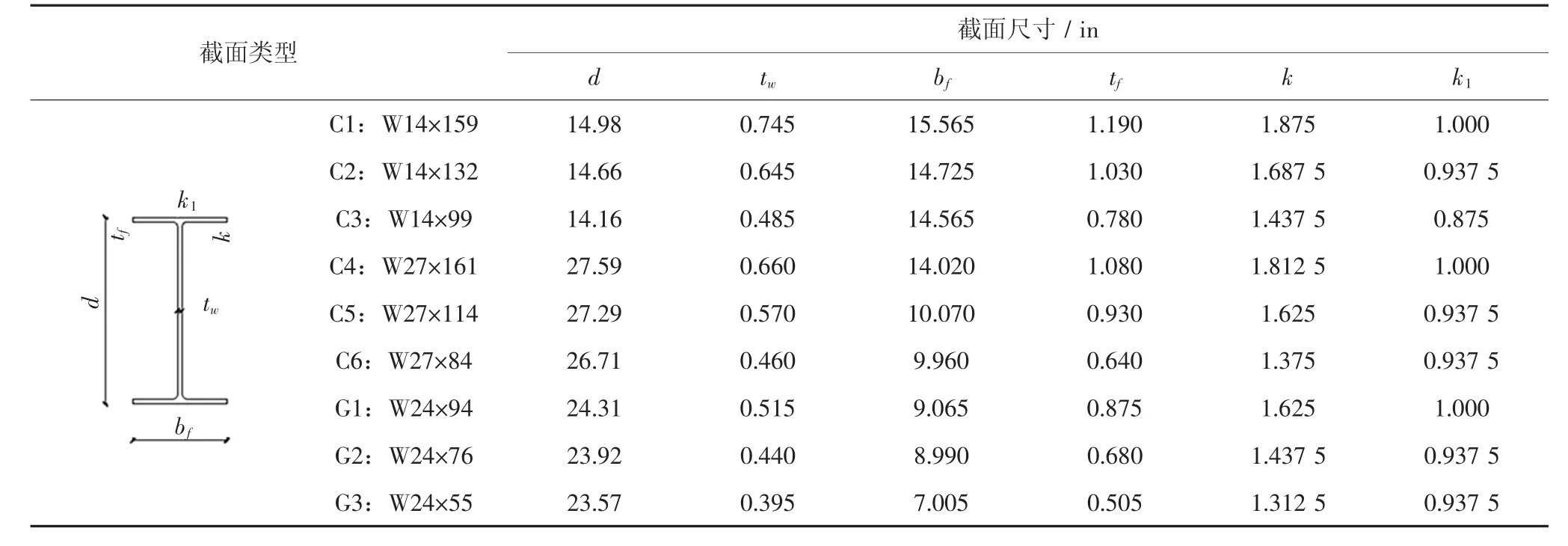
表1 框架構件截面形式Tab.1 Section for frame members

通過估計SGLD模型參數的3 000個樣本可以計算Gumbel Copula的參數值，其中，τ?n=0.738 0，θ=10.42.由此，可以確定結構反應聯合分布的Gumbel Copula，并得到本例所考慮結構體系的微小失效概率.結構體系微小失效概率的計算結果見圖3，圖3還給出了由基于30 000個樣本的Monte Carlo方法的計算結果.圖3中坐標系的橫軸表示各層的彈性位移比限值，縱軸表示結構微小超越概率.圖3表明：由Gumbel Copula得到的失效概率與Monte Carlo模擬結果幾乎完全吻合，說明Gumbel Copula是結構可靠度分析的可靠方法，其計算效率是Monte Carlo方法的5～10倍.

圖3 結構體系的微小失效概率Fig.3 Small failure probabilities of the structure

6 結論

本文建立了一種基于Copula函數和SGLD模型的結構系統可靠度分析方法，通過一個6層鋼結構系統的可靠度分析，驗證了本文所建立方法的有效性和精確性.

本項研究的主要結論為：

1）結構系統反應的分布尾部可由SGLD模型來近似，而矩方法可以精確地估計SGLD模型參數.

2）Gumbel Copula可被用于高維結構系統可靠度評估中的聯合失效概率計算，該方法的計算精度比Monte Carlo方法高，其計算效率是Monte Carlo方法的5～10倍.

3）本文方法需要利用一定容量的反應樣本來估計的SGLD模型和Copula模型的參數，反應樣本可由Monte Carlo方法生成，樣本容量可以在3 000～5 000之間.

4）本文方法適用于大多數具有確定性解的工程結構可靠度分析，同時對其他類型Copula函數的應用具有重要的參考價值.

[1]ZhaoYG，Ono T.A general procedure for first/second-order reliability method[J].Structural Safety，1999，21（2）：95-112.

[2]Rosenblueth E.Point estimation for probability moments[J].Proceedings of the National Academy of Science，1975，72（10）：3812-3814.

[3]Zhao YG，Ono T.Moment method for structural reliability[J].Structural Safety，2001，23（1）：47-75.

[4]XiongF，GreeneS，ChenW，etal.Anewsparsegridbasedmethodfor uncertaintypropagation[J].StructuralandMultidisciplinaryOptimization，2010，41（3）：335-349.

[5]Faravelli L.Response-surface approach for reliability analysis[J].Journal of Engineering Mechanics，ASCE，1989，115（12）：2736-2781.

[6]Deng J，Gu D，Li X，et al.Structural reliability analysis for implicit performance functions using artificial neural network[J].Structural Safety，2005，27（1）：25-48.

[7]Au S K，Beck J L.Important sampling in high dimensions[J].Structural Safety，2002，25（2）：139-163.

[8]Song S F，ZZ Lu，HW Qiao.Subset simulation for structural reliability sensitivity analysis[J].Reliability Engineering and System Safety.2009，94（2）：658-665.

[9]Miao F，Ghosn M.Modified subset simulation method for reliability analysis of structural systems[J].Structural Safety，2011，33（4）：251-260.

[10]Lu ZZ，Song SF，Yue ZF，et al.Reliability sensitivity method by line sampling[J].Structural Safety，2008，30（2）：517-532.

[11]Jinsuo N，Ellingwood BR.Directional methods for structural reliability analysis[J].Structural Safety，2000，22（3）：233-249.

[12]Ditlevsen O.Narrow reliability bounds for structural system[J].Journal of Structural Mechanics，1979，7（4）：453-472.

[13]Zhang Y C.High-order reliability bounds for series systems and application to structural systems[J].Computers&Structures，1993，46（2）：381-386.

[14]SongJH，KiureghianAD.Boundsonsystemreliabilitybylinearprogramming[J].JournalofEngineeringMechanics，ASCE，2003，129（6）：627-636.

[15]Nelsen RB.An introduction to copulas[M].New York：Springer：2006.

[16]Serkan E，Multivariate copula based dynamic reliability modeling with application to weighted-k-out-of-n systems of dependent components[J]. Structural Safety，2014，51：23-28.

[17]Low Y M.A new distribution for fitting four moments and its applications to reliability analysis[J].Structural Safety，2013，42：12-25.

[18]GenestC，NeslehovaJ，GhorbalNB.EstimatorsbasedonKendall’stauinmultivariablecopulamodels[J].JAustNZJStat，2011，53（2）：157-177.

[19]Nowak AS，Collins KR.Reliability of structures[M].New York：McGraw-Hill，2000.

[責任編輯 楊屹]

Estimation of the reliability of structural system based on Gumbel Copula

WU Jinhua，HE Jun

（College of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiaotong University,Shanghai 200240,China）

This paper aims to propose a method to estimate the failure probability of high reliability structural system based on Gumbel Copula.The marginal distributions of responses of structures are modeled by the shifted generalized lognormal distribution(SGLD)and the joint distribution is obtained by Copula functions.The parameter of Copula functions required can be estimated by the moment method.With this method,the estimation of reliability of a six-story steel frame structure system under earthquake loads shows that the marginal distribution expressions and joint distribution expressions of responses of structure system can be accurately given by the proposed method and the numerical precision and calculation effectiveness are high.

Copula function;the reliability of structural system;the shifted generalized lognormal distribution;probability distribution;parameter estimation

O241/O242

A

1007-2373（2017）03-0094-06

10.14081/j.cnki.hgdxb.2017.03.017

2016-12-26

上海市自然科學基金（16ZR1417300）；教育部留學回國人員啟動基金（14Z102050011）.

吳金華（1990-），男，碩士研究生，wjhsjtu@yeah.net.通訊作者：何軍（1968-），男，副教授，博士，junhe@sjtu.edu.cn.