海上大氣折射率的相似性研究

郭相明，康士峰，趙棟梁，張玉生

(1.中國海洋大學海洋與大氣學院，山東青島 266003；2.中國電波傳播研究所電波環境特性及模化技術重點實驗室，山東青島 266107)

海上大氣折射率的相似性研究

郭相明1,2，康士峰2，趙棟梁1，張玉生2

(1.中國海洋大學海洋與大氣學院，山東青島 266003；2.中國電波傳播研究所電波環境特性及模化技術重點實驗室，山東青島 266107)

基于邊界層相似理論，通過數值模擬的方法研究了大氣折射率的相似性，數值模擬結果顯示大氣折射率在不穩定大氣條件和近中性條件下大氣折射率近似滿足相似理論，在穩定大氣條件下大氣折射率不滿足相似理論假設。其次通過氣象梯度塔測量的水文氣象參數計算的大氣折射率剖面和開路渦度系統測量的數據計算的相似性特征量，實驗研究了大氣折射率的相似性，研究也表明大氣折射率在穩定大氣條件下不滿足相似性。

大氣折射率；相似理論；海洋大氣邊界層

1 引言

大氣中的微波傳播直接依賴大氣折射率的變化特征，為此通常采用大氣折射率來描述大氣無線電波傳播物理機制[1]。基于大氣折射率的垂直梯度特征可劃分為4類，即次折射、正常折射、超折射和波導折射。在微波波段，大氣折射率可以表達為大氣溫度、濕度和氣壓的非線性函數[2-3]，因此可以通過氣象傳感器測量大氣溫度、濕度和氣壓的方式確定大氣折射率的結構特征，例如氣象上常用的高空探測系統和低空系留探空系統成為探測大氣折射率的有效途徑。

從20世紀50年代邊界層相似理論的提出，對邊界層的研究具有開創性的意義，相似性理論在描述大氣邊界層，特別是近地層研究與應用中發揮了極大的作用[4-5]。基于相似理論，可以采用近地（海）面一層大氣溫度、濕度、氣壓和風速，以及海面溫度來確定近海面的大氣溫度、濕度和風速剖面，為近地海面大氣折射率剖面構建提供了理論基礎和方法支撐，同時認為近海面大氣壓近似靜態平衡，并滿足壓高公式，基于此提出了許多基于相似理論的近海面折射率剖面預測方法和蒸發波導模型[6-10]。由于大氣折射率為大氣溫度、濕度和氣壓的非線性函數，于是有研究者也認為大氣折射率或其位大氣折射率為相似量[11]，不過從20世紀90年代以來，Hill[12]指出，大氣折射率作為相似量是有一定的條件限制，Cook等[13]通過數值模擬的方式指出，大氣位折射率僅在不穩定和近中性條件下可以看作為相似量，在1993年，Sorbjan[14]指出當重新定義折射率特征量的情況下，折射率方差可以看作為相似量。

長期以來，雖然有學者指出大氣折射率不能看作為相似量，但在實際應用中又往往把其看作為相似量，同時由于條件限制，雖然通過數值模擬的方式指出不為相似量，但缺乏有效的實驗手段進行驗證，為此本文從數值模擬和實驗的角度全面闡述大氣折射率的相似性。

2 大氣折射率相似性原理

2.1 大氣折射率及其擾動

在無線電氣象學中大氣折射指的是電磁波在大氣介質中傳播的彎曲特性，其折射程度用折射指數n來衡量，定義為電波在自由空間中的傳播速度c（光速）與介質中的傳播速度v的比值：

地球表面大氣折射指數的正常值一般在1.000 25和1.000 4之間。對于電波傳播研究，由于數值較小，n值不方便實際應用。因此，定義了一個與折射指數可換算的量即通常使用的大氣折射率N。在微波及以下頻段，大氣折射指數n或大氣折射率N可由常規氣象要素確定，其關系為：

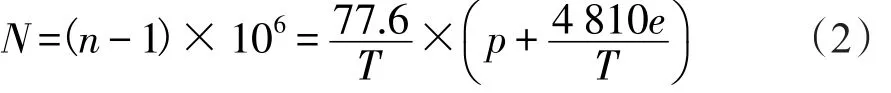
式中：p為氣壓（hPa），e為水汽壓（hPa），T為氣溫（K）。考慮水汽壓e和比濕q之間關系為：

式中：ε為氣體常數，通常取0.622。把上式代入式（2）得：

因此，大氣溫濕度和氣壓的變化或擾動將引起大氣折射率的變化或擾動。在固定高度，大氣折射率的擾動N'可以表達為[15]：

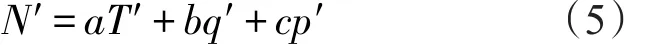
忽略氣壓擾動，則大氣折射率擾動可以表達為[12]：

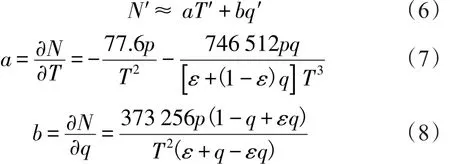
2.2 標量相似理論和原理

相似性理論是描述大氣邊界層，特別是近地層研究的有力工具。在近地層相似理論中，采用包括相似長度、摩擦速度、溫濕度的尺度參數和其它尺度參數，距離地面海面的高度，來描述邊界層大氣參數的變化特征。前蘇聯的莫寧最早在1946年采用白漢金Π定理[16]，將摩擦速度u*，感熱通量以及浮力因子進行組合得到一個具有長度量綱的特征量，現稱莫寧-奧布霍夫相似長度來描述的大氣的狀態，其定義為[17]：

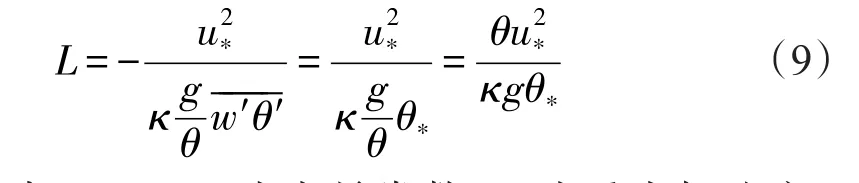
式中：k=0.4，為卡曼常數；g為重力加速度；w′和θ′分別為垂直風速和位溫脈動量；u*和θ*分別為摩擦速度和位溫的尺度參數，代表近地（海）面湍流垂直輸送的強度；“-”代表整體平均。莫寧-奧布霍夫長度反映了雷諾應力和浮力做功的相對大小，并定義L＞0時，大氣穩定，L＜0，不穩定，

|L|→∞，大氣中性。隨后，1954年莫寧和奧布霍夫最終提出了完善的近地層相似理論。其中尺度參數的定義：

式中：q′大氣比濕脈動量；q*為比濕的尺度參數。需要說明的是，在近地面層由于位溫和溫度相差很小通常假定T*≈θ*來定義溫度特征尺度。

與溫濕度尺度參數定義相似，大氣折射指數尺度參數或大氣折射率尺度參數定義為：

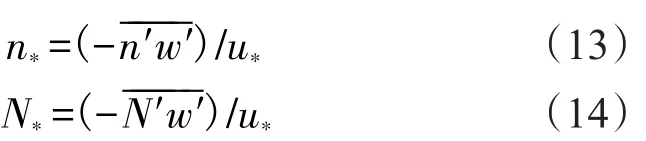
在近地（海）面，風速、溫度和濕度的無量綱化普遍廓線方程為：

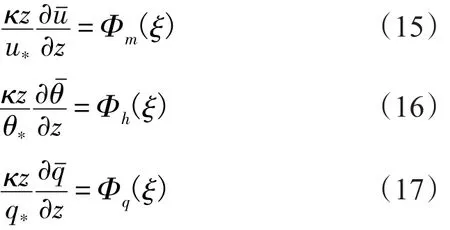
同樣，通常基于大氣折射率是溫度和濕度函數的原理，假定大氣折射率同樣滿足相似理論，即

3 基于數值模擬的大氣折射率相似性研究

3.1 數值模擬方法

首先采用數值模擬的方式確定大氣折射率是否可以看作為相似量，是否滿足相似理論。基于相似理論，式（15）—（17）對應的積分形式，即近地層內水平風速u、位溫θ、比濕q的垂直廓線表示為[18]：

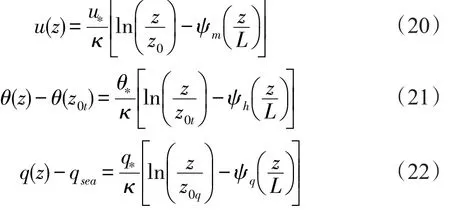
基于位溫剖面確定的溫度剖面為：

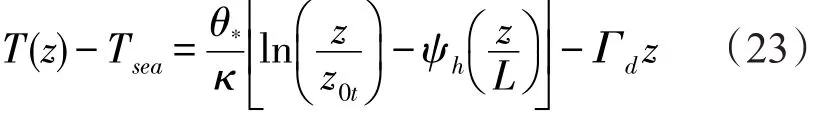
式中：u(z)、θ(z)、q(z)分別是高度z處的水平風速、位溫和比濕；z0t和z0q分別為溫度和濕度粗糙度；ψh和ψq分別位溫和濕度普適函數，通常取二者相等；Γd為干絕熱遞減率，約等于0.009 76 K/m；Tsea、qsea分別是海面溫度和比濕，且考慮海水鹽度對比濕的影響，qsea=0.98qsat(Tsea)、qsat(Tsea)為基于海面溫度計算的海面飽和比濕。目前主要采用海洋-大氣耦合響應試驗（Tropical Oceans Global Atmosphere，TOGA-Coupled Ocean Atmosphere Response Experiment，COARE）發展起來的海氣通量整體算法COARE進行位溫θ、比濕q的特征尺度θ?、q?的計算[19]，考慮到目前海氣通量整體算法已更新到3.0版本[20]，因此本文采用最新發布的COARE3.0算法確定海表層尺度參數和海面粗糙度，進行大氣溫濕剖面的計算。

為了確定近海面大氣折射率剖面，還要確定大氣壓剖面，通過聯立流體靜力學方程和理想氣體定律并積分得到，即[18]

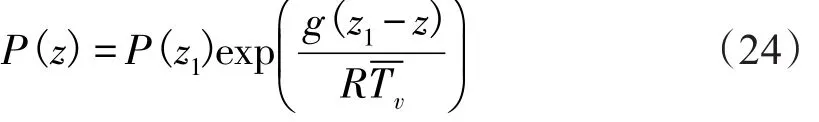
式中：R為干空氣氣體常數；g為重力加速度；P(z1)測量高度z1的氣壓，P(z)為計算高度z的氣壓；為高度z1和高度z處的平均虛溫。根據式（20）—（24）確定的溫度、比濕和氣壓剖面，代入折射率公式就可以確定大氣折射率剖面，進而可以確定不同的大氣穩定度條件下，不同高度的大氣折射率梯度。

3.2 數值模擬結果

假定在10 m高度處測量的空氣溫度從12℃變化到21℃，間隔0.25℃，相對濕度取80%，風速4 m/s，氣壓1 022.07 hPa，海表溫度18℃，按照上述方法分別計算大氣的穩定度和對應的式（18）的左端，結果見圖1。與圖1條件類似，圖2給出了相對濕度從40%變化到95%時，其它模擬條件不變時，大氣折射率相似函數的變化情況。

由圖1、2可見，所有的計算曲線并沒有完全在一條曲線上，但在不穩定或近中性大氣條件下，曲線近似在一條直線上，而在穩定大氣條件下，特別是強穩定條件下曲線更為發散。因此，可以初步確定大氣折射率在穩定大氣條件下不滿足相似理論。

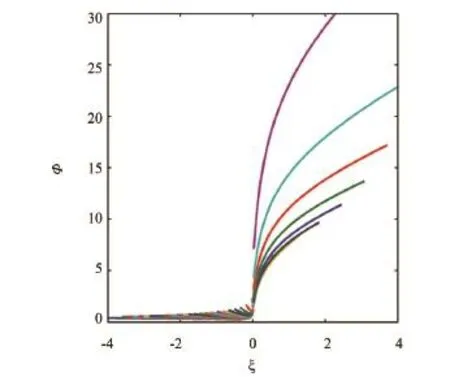
圖1 不同氣-海溫差下的大氣折射率相似函數ΦN變化

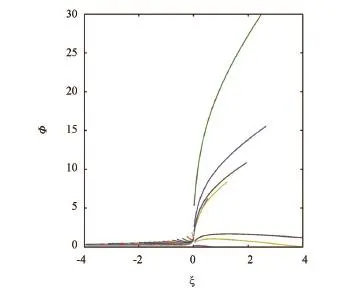
圖2 相對濕度變化時大氣折射率相似函數ΦN變化

4 基于實驗數據的大氣折射率相似性研究

4.1 實驗簡介與數據處理

為研究大氣折射率的相似性，在渤海某海域開展了實驗[18]。觀測儀器架設某小島岸邊的鐵塔上，鐵塔塔基大部時間被海水所淹沒，在海風作用下近似代表了附近海域大面積海洋下墊面的特性，在維薩拉海用自動氣象站MAWS420的基礎上進行了傳感器擴展[21]，在距離塔基平臺6、10、15、20、27、34 m處架設溫濕度傳感器，在6、15、27 m處架設風速傳感器，同時在第二層觀測平臺上（10 m）安裝了氣壓傳感器和紅外海溫傳感器，所有氣象傳感器采集的數據存儲在采集卡中，所有數據的采樣頻率為每分鐘一次，具有實時和連續的優點。在塔基高度10 m處，在鐵塔上架設渦動開路協方差系統，為了盡可能地避免塔體對測量的影響，CSAT3三維超聲風速儀和LI7500開路氣體分析儀盡量遠離塔體架設（距塔體約2 m）。渦動協方差系統采樣頻率為10 Hz，采樣時間每次30 min。基于原始觀測資料，經過去趨勢、坐標旋轉等處理后計算出近海層特征尺度（u*、θ?、q?）、穩定度參數ξ等，進而確定折射率特征尺度。

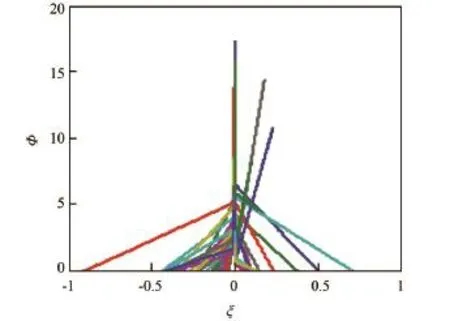
圖3 實驗期間大氣折射率相似函數ΦN剖面隨大氣穩定度ξ的變化

為了確定不同高度的大氣折射率梯度，基于氣象梯度塔測量的大氣參數和海面溫度，進行同時間段30 min的平均，在靜力平衡和理想氣體假設下，利用壓高公式將10 m處氣壓換算到其他高度層上，然后利用式（2）和（3），可以計算不同高度層上的M值，假定海面相對濕度為100%，確定海面大氣折射率，然后對7層修正折射率進行非線性最小二乘擬合，可以確定大氣修正折射率剖面所用的擬合公式為：

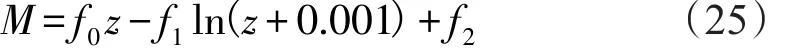
式中：M代表修正折射率；z代表高度；f0、f1、f2為擬合系數。在此需要指出的是在近海面大氣折射率的計算中，采用了海面為飽和水汽的假設，同時在實際的計算過程中，必須考慮潮位的影響，本文在數據處理過程中，利用潮汐數據對氣象傳感器的實際距離海面的高度進行了訂正。根據大氣折射率和修正折射率的關系則可確定對應的大氣折射率剖面，可確定不同高度的大氣折射率梯度值。

4.2 實驗結果

取對應時間段渦動開路協方差采集的數據和氣象梯度儀采集的數據計算大氣折射率特征量、大氣穩定性和對應高度的大氣折射率梯度值，計算不同穩定度條件下大氣折射率普適函數。圖3給出了實驗期間，海風影響下大氣折射率普適函數隨大氣穩定度變化情況。

由圖3可見，所有的曲線并沒有完全在一條曲線上，在不穩定大氣條件下與數值模擬結果不同，表現出更加的分散性，這可能受實驗條件的限制，在海岸區域受來自陸地氣流的影響，不能完全代表廣闊海域的實際海洋環境，雖然在數據處理過程中考慮了測量誤差，但是不可避免的也存在測量誤差和環境代表性問題，使得在不穩定大氣條件也顯示出很強的分散性。在穩定大氣條件下所有的曲線相對模擬結果表現出更強的分散性。不過在近中性條件下，曲線還是表現出一定的匯聚趨勢。因此，也可以初步確定大氣折射率在海上實驗環境下表現出不滿足相似量的假設，不滿足標量相似理論，特別是在穩定大氣條件下。

5 結論與討論

長期以來，考慮大氣折射率為溫度、濕度和氣壓的函數，以及大氣溫濕度在近地（海）面層滿足相似理論，將其看作為相似量，并在許多方面得到了廣泛的應用。例如折射率結構常數的確定和近海面蒸發波導模型的構建等。本文通過數值模擬和觀測實驗兩種途徑論述了大氣折射梯度是否滿足相似理論，大氣折射率是否可以看作為相似量，基于數值模擬和實驗結果顯示大氣折射率梯度在穩定大氣條件下不滿足相似理論，大氣折射率不為相似量。

在此需要指出，（1）由于受實驗條件的限制，試驗結果顯示在不穩定大氣條件下大氣折射率梯度也不滿足相似理論，與數值模擬結果不一致，需要開展海上實驗進一步驗證；（2）大氣折射率不僅是溫、濕度的函數，同時大氣壓強也是一個重要的量，在上述定義大氣折射率特征尺度量時忽略了大氣壓強的影響；（3）在折射率結構常數的定義中，考慮了溫度和濕度的相關性對折射率結構常數的影響，因此在定義大氣折射率特征尺度時考慮大氣溫度和濕度在不同的穩定度條件下相關性對大氣折射率的影響，大氣折射率梯度有可能滿足相似理論；（4）在相似函數的定義中，僅考慮了大氣穩定度對大氣參數梯度的影響，Fairall等[19]指出，除了大氣穩定度外，邊界層高度、地海面粗糙度等也是一個重要的因素，因此發展更為完善的相似理論也有可能使大氣折射率滿足相似理論。

致謝：感謝中科院大氣物理所王介民研究員編著的《渦動相關通量觀測指導手冊》2012版對實驗和數據處理的指導。

[1]Atkinson B W,Li J G,Plant R S.Numerical modeling of the propagation environment in the atmospheric boundary layer over the Persian Gulf[J].Journalof Applied Meteorology and Climatology,2000,40(3):586-603.

[2]Babin S M,Dockery G D.LKB-based evaporation duct model comparison with buoy data[J].Journal of Applied Meteorology and Climatology,2001,41(4):434-446.

[3]Bean B R,Dutton E J.Radio meteorology[M].Washington D.C.: United States,Government Printing Office,1966:435.

[4]Businger J A,Wyngaard J C,Izumi Y,et al.Flux-profile relationshipsin theatmospheric surface layer[J].Journalofthe Atmospheric Sciences,1971,28(2):181-189.

[5]Gryning S E,Batchvarova E,Brümmer B,et al.On the extension of the wind profile over homogeneous terrain beyond the surface boundary layer[J].Boundary-Layer Meteorology,2007,124(2): 252-268.

[6]Paulus R A.Practical application of an evaporation duct model[J]. Radio Science,1985,20(4):887-896.

[7]Babin S M,Young G S,Carton J A.A new model of the oceanic evaporation duct[J].Journal of Applied Meteorology,1997,36(3): 193-204.

[8]Ivanov V K,Shalyapin V N,Levadnyi Y V.Determination of the evaporation duct height from standard meteorological data[J]. Izvestiya,Atmospheric and Oceanic Physics,2007,43(1):36-44.

[9]Newton D A.COAMPS modeled surface layer refractivity in the roughness and evaporation duct experiment 2001[D].California: Naval Postgraduate School,2003:7-9.

[10]Ding J L,Fei J F,Huang X G,et al.Development and validation of an evaporation duct model.Part II:evaluation and improvement of stability functions[J].Journal of Meteorological Research, 2014,29(3):482-495.

[11]Gossard E E.The height distribution of refractive index structure parameter in an atmosphere being modified by spatial transition at its lower boundary[J].Radio Science,1978,13(3):489-500.

[12]Hill R J.Implications of Monin-Obukhov similarity theory for scalar quantities[J]Journal of the Atmospheric Sciences,1989,46 (14):2236-2244.

[13]Cook J,Burk S.Potential refractivity as a similarity variable[J]. Bound-Layer Meteorology,1992,58(1-2):151-159.

[14]Sorbjan Z.Monin-Obukhov similarity for refractive index revisited [J].Journal of the Atmospheric Sciences,1993,50(21):3677-3684.

[15]Gossard E E.Refractive index variance and its height distributionin different air masses[J].Radio Science,1977,12(1):89-105.

[16]郭相明,康士峰,張玉生,等.蒸發波導模型特征及其適用性研究[J].海洋預報,2013,30(5):75-83.

[17]盛裴軒,毛節泰,李建國,等.大氣物理學[M].北京:北京大學出版社,2003:247-250.

[18]郭相明,康士峰,韓杰,等.蒸發波導數據庫及中國海域的統計分析[J].電波科學學報,2013,28(6):1152-1157,1182.

[19]Fairall C W,Bradley E F,Rogers D P,et al.Bulk parameterization of air-sea fluxes for tropical ocean-global atmosphere coupledocean atmosphere response experiment[J].Journal of Geophysical Research:Oceans,1996,101(C2):3747-3764.

[20]Fairall C W,Bradley E F,Hare J E,et al.Bulk parameterization of air-sea fluxes:updates and verification for the COARE algorithm [J].Journal of Climate,2003,16:571-591.

[21]范建業,高山紅,康士峰,等.基于氣象梯度儀的蒸發波導探測[J].無線電工程,2012,42(11):32-33.

Study on the similarity of ocean atmospheric refractivity

GUO Xiang-ming1,2，KANG Shi-feng2，ZHAO Dong-liang1，ZHANG Yu-sheng2
（1.College of Oceanic and Atmospheric Sciences,Ocean University of China,Qingdao 266003 China; 2.National Key Laboratory of Electromagnetic Environment，China Research Institute of Radiowave Propagation,Qingdao 266107 China）

Based on Monin-Obukhov similarity theory,using the numerical method to validate whether the radio refractivity behave as a similarity variable,numerical results show that the vertical gradient of radio refractivity does not collapse to a single atmospheric stability universal function,but under unstable and near neutral conditions the radio refractivity approximately behave as a similarity variable.Using the hydrometeorology parameters measured by the meteorology grads tower to determine the radio refractivity profile,and with the turbulence data observed using the open path eddy covariance system,experiment results show that the vertical gradient of radio refractivity also does not collapse to a single atmospheric stability universal function when the atmosphere condition is stable.

radio refractivity;similarity theory;marine atmospheric boundary layer

P732.6

A

1003-0239（2017）03-0071-06

10.11737/j.issn.1003-0239.2017.03.009

2016-09-04；

2016-10-18。

國家自然科學基金（41175012）。

郭相明（1981-），男，工程師，博士在讀，主要從事海洋環境與電波傳播方面的研究。E-mail:xmguo08@163.com