基于GNSS信號信噪比觀測量的海平面高度變化研究

胡 媛，劉 衛，周 悅，王一津，俞子恒

（1.上海海洋大學 工程學院，上海 201306；2.上海海事大學 商船學院，上海 201306）

基于GNSS信號信噪比觀測量的海平面高度變化研究

胡 媛1，劉 衛2，周 悅1，王一津1，俞子恒1

（1.上海海洋大學 工程學院，上海 201306；2.上海海事大學 商船學院，上海 201306）

建立基于GNSS信號的海面測高數學模型，揭示基于載波和信噪比觀測量測高方法的內在聯系；提出利用造價便宜的GPS接收機以及普通接收機天線進行海平面高度變化監測的手段；進行海平面高度變化監測的實驗并與驗潮儀對比分析。結果表明：利用普通GPS接收機和天線進行海平面測高可以獲得厘米級的測量精度，24 h連續監測的均方根誤差為4.13 cm，GPS高度計與驗潮儀的測量結果相關系數為0.86；所布設的GNSS高度計與造價昂貴的大地測量型接收機監測結果相當，該造價便宜的高度計更適合用于未來大規模實際的海平面高度變化監測中。

GPS；信噪比；海平面高度；衛星導航

1 引言

隨著全球氣候變暖，海面平均高度的升高已經逐漸影響著各個沿海國家的經濟和社會發展情況；對海平面高度變化的長期和準確的監測具有很重要的現實意義[1-2]。傳統的海平面高度監測依靠布置在沿海各個站點的驗潮儀進行觀測和記錄海面變化情況。驗潮儀只監測海平面高度對于基準點的相對變化。即使很精確的驗潮儀，其監測結果不僅受海平面高度變化的影響，同時也受地殼運動的影響。地殼運動和變形等的影響使得傳統的驗潮儀很難實現對海平面高度變化的直接測量[3-4]。

隨著GPS（Global Positioning System）、GLONASS（Global Navigation Satellite System）、北斗（Bei Dou Navigation Satellite System，BDS）以及Galileo等全球衛星導航系統（Global Navigation Satellite System，GNSS）的迅速發展，利用GNSS反射信號進行海平面高度變化的監測已經成為可能[5-8]。1993年，Martin-Neira[9]首次提出利用GPS散射信號進行海平面高度測量的可能性。研究人員陸續開展了利用GPS反射信號進行海平面高度測量的研究，主要包括：（1）利用GPS的載波觀測量進行海平面高度測量的研究[10-11]；基于載波觀測量的測量需要布設兩個接收機天線，一個天線接收直射信號，另外一個天線接收來自于海面的反射信號。該方法精度相對較高，但是安裝麻煩、費用較高，隨著海面風速增高，測量精度嚴重下降；（2）利用大地測量型接收機所接收到的信號信噪比（SNR）進行海平面高度的測量研究[12-13]；這些研究所用的大地測量型接收機價格昂貴，接收機采用扼流圈天線并配置球形保護罩以提高天線增益高，很難進行大規模的海平面高度監測實際應用。另外，利用載波觀測量和信噪比SNR的兩種海面測高方法的內在聯系及測量機理也有待進一步研究。

本文研究利用GNSS觀測量進行海平面高度監測的方法；以GPS系統為例，建立基于載波觀測量和信噪比SNR的海面測高數學模型，研究兩種方法內在聯系和統一性問題；針對傳統監測方案造價高、安裝復雜，很難進行大規模應用的實際，本文構建了利用造價便宜的GPS接收機以及普通接收機天線進行海平面高度變化監測的手段，并進行實驗分析研究，可為未來海洋監測設備的更新換代和大規模實際應用提供技術參考。

2 GNSS海面測高方法

2.1 GNSS反射信號測高原理

傳統的GNSS接收機只是利用所直接接收到的導航信號進行定位和導航。GNSS導航信號屬于電磁波信號，其經過地面的反射會被天線接收而降低導航定位精度，這種現象稱為多路徑干擾[14-15]。而基于GNSS反射信號進行地面參數的測量正是利用導航信號的多路徑干擾效應，海平面高度變化的監測原理正是利用經過地面的反射的信號進行測量。假設接收機接收到第s顆衛星的信號，同時第s顆衛星的信號經過海面的反射也被天線接收到（見圖1）。信號在海面的反射點為O點；接收機天線距離海平面高度為h；信號的反射角為；反射信號與直接信號相比，額外的傳輸路徑為ρ，如圖中粗實線表示。

根據GNSS信號的傳輸原理，接收機天線接收到第s顆衛星的合成信號（包括直接信號和反射信號）為[16]：

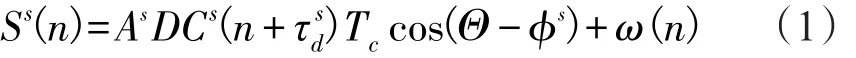
式中：

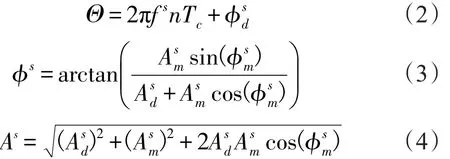
As和?s分別為接收機接收到的合成信號的幅度和相位角；D為信號的導航電文信息；Cs(·)為信號的偽隨機碼；Tc為偽隨機碼的周期；和分別為所接收到的直射信號和反射信號的幅值；?sd為直射信號的載波相位，為反射信號的載波相位；ω(n)為方差為1的高斯白噪聲。

2.2 SNR觀測量測高模型

假設接收到的信號噪聲為高斯白噪聲，As為正則化的幅值，因此As直接提供了信噪比的觀測量，即：

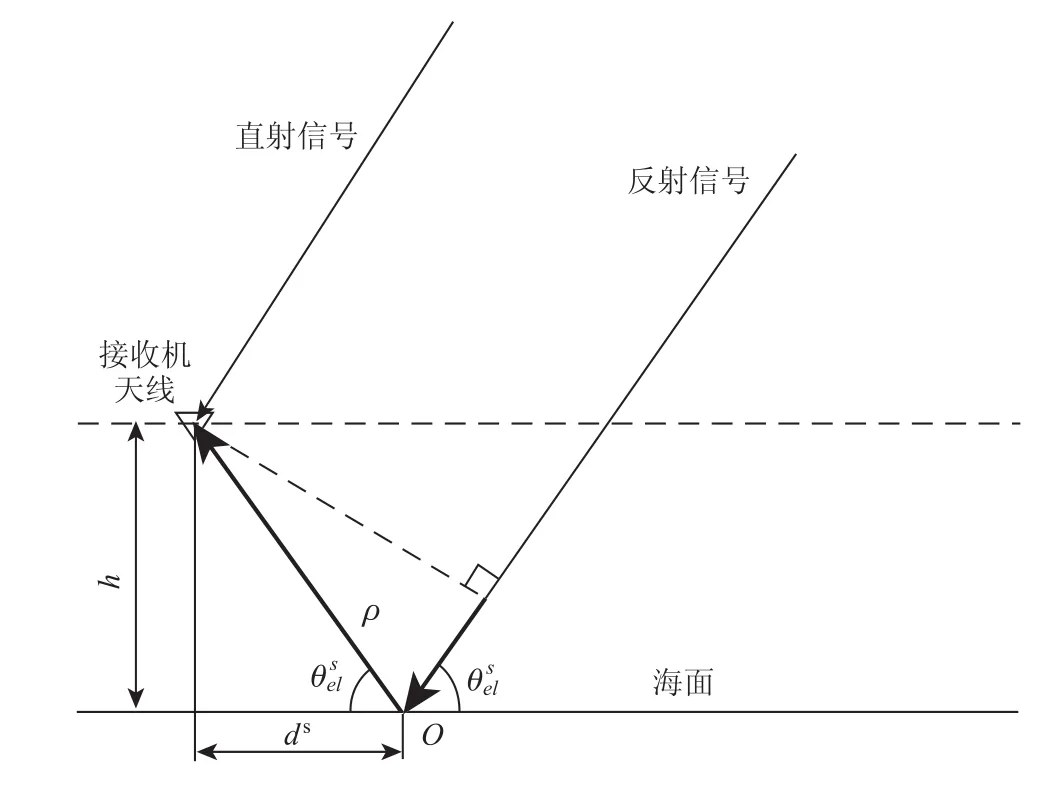
圖1 GNSS海面測高示意圖

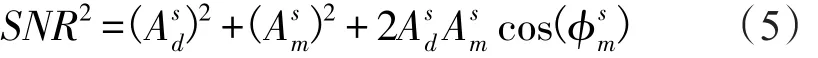
式（5）為基于GNSS信號信噪比SNR的海平面高度測量的基本數學關系式，利用接收機的SNR觀測值輸出時間序列就可以進行海平面高度的測量。可以看出，SNR的主要組成部分為直接信號的幅值，反射信號對SNR的影響主要是產生高頻的小幅度的變化，一般而言，這種小幅度的振蕩是在比較小的衛星仰角情況下產生的，因此在海面測高時仰角通常選用30°以下。

根據圖1的GNSS測高幾何關系，可以得到反射信號超過直接信號的額外傳輸距離ρ與接收機天線距離海平面高度h和信號反射角的關系為：

式（6）為利用載波觀測量進行海面測高的基本數學關系式[17-18]，通過獲得反射信號超過直接信號的額外傳輸距離和衛星的高度角，可以獲得接收機天線距離海平面高度h。

根據光速c、信號頻率 f0以及反射信號的載波相位的關系，式（6）可以變換為：

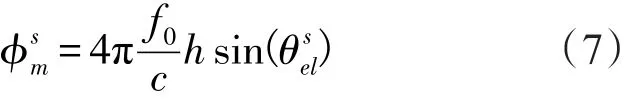
根據式（5）和式（7），無論是利用信噪比SNR或載波觀測量的海面測高方法，都是基于反射信號的載波相位進行測量的。基于載波觀測量的方法直接選用載波相位作為觀測量，測高接收機的輸出數據為載波相位，而基于信噪比SNR的方法在載波相位基礎上選用SNR作為觀測量，測高所利用的是接收機的SNR輸出時間序列。兩種方法的測量基礎是統一的，而且利用信噪比SNR的測量方法不需要改造傳統的接收機內部結構和安裝接收反射信號的天線，可以直接利用普通接收機的SNR輸出量就可以進行海平面高度的監測。

3 測高實驗與分析

3.1 實驗過程

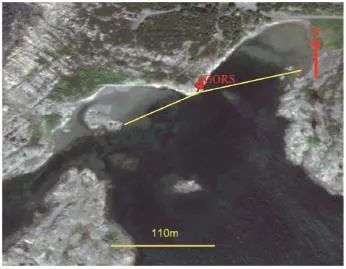
圖2 GPS海平面測高實驗區域

圖3 GPS海平面測高接收機

實驗場地為沿海區域，海面風速基本都在2 m/s以上，接收機所面向的海域無地形遮擋區域的方位角范圍為70°～210°（見圖2）。測站配置了佳瓦特普通GPS接收機（見圖3，GORS為接收機所在位置），接收機安裝在水泥墩上。與傳統配置有球形保護罩的扼流圈天線大地測量型接收機不同，本實驗中的接收機天線為普通型GPS接收機天線，由GPS接收機和采集數據裝置構成了GPS高度計。實驗時間為2015年7月1日00：00：00（世界時，下同）至7月2日00：00：00，連續記錄24 h的GPS L1信號的SNR觀測值，數據記錄時間間隔為1 s。實驗中接收機天線相位中心距離海平面高度大約3 m左右；為了實現連續有效的測量，衛星高度角設置為5°～30°。另外實驗還專門安裝了驗潮儀記錄海面變化情況，安裝位置離所配置的接收機大約為1 km左右，驗潮儀的測量結果可以與GPS所獲得結果進行對比。

實驗方案及流程見圖4，首先需要安裝實驗設備并進行數據采集，接收機所采集的數據為Rinex觀測值文件，同時利用GNSS星歷數據將o文件轉換為信噪比SNR數據，這些信噪比SNR時間序列按照不同衛星和接收時間進行排列。

3.2 SNR測高結果及分析

選擇不同衛星的時間序列將直接信號分量濾除，正如式（5）所描述，濾除的結果為包含相位信息的反射信號分量；將所濾除的信號按照衛星高度角進行序列重構，衛星高度角的范圍限制為5°～30°。圖5以碼段編號為PRN 5和PRN16的兩顆GPS衛星為例，表示SNR序列在濾除直接信號后的SNR分量隨衛星仰角變化情況。

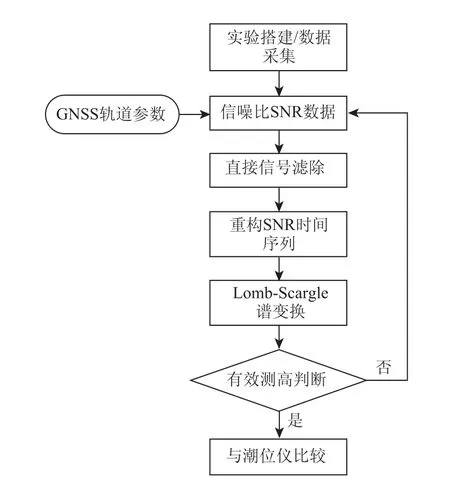
圖4 GNSS海面測高流程

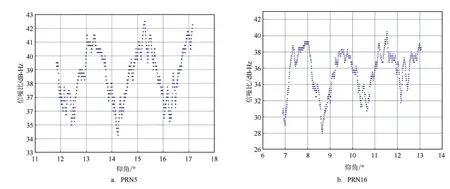
圖5 不同碼段GPS衛星信噪比SNR隨仰角變化情況

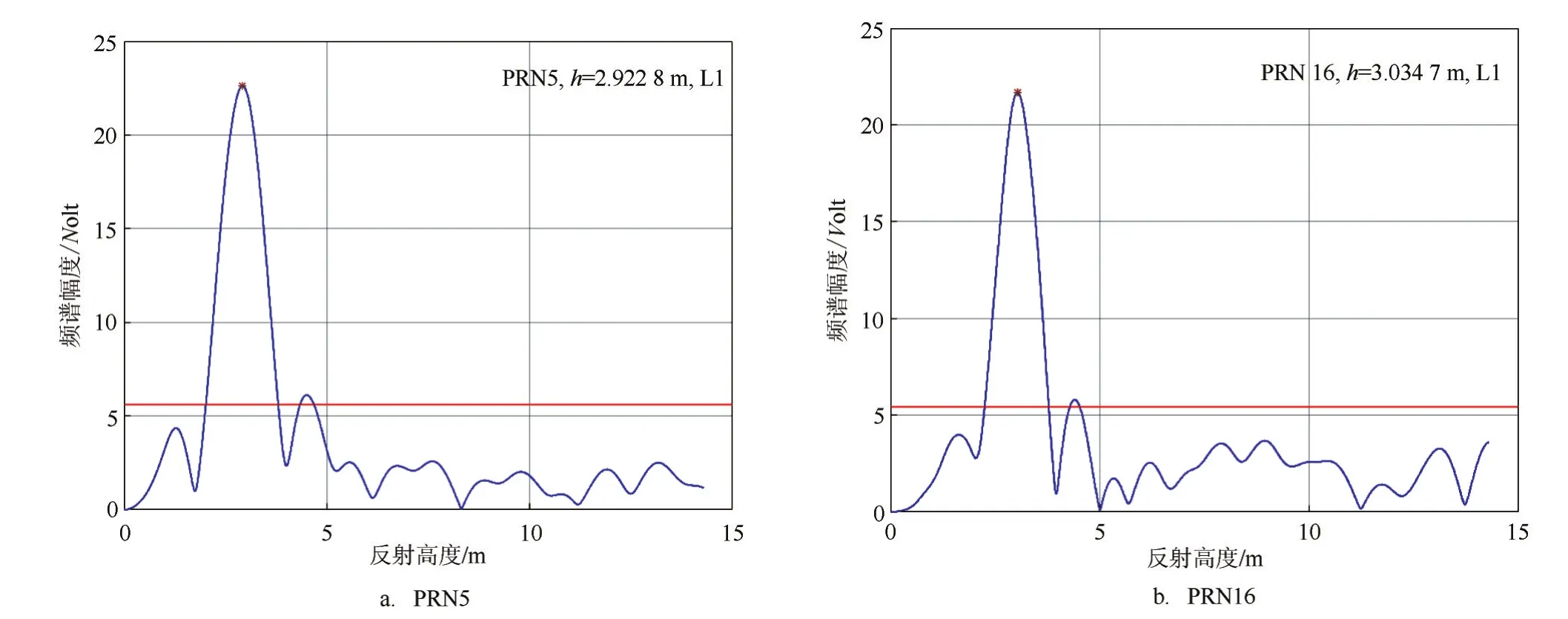
圖6 不同碼段編號的GPS衛星的LSP頻譜分布情況

根據濾除直接信號分量所獲得的信噪比重構序列，進行Lomb Scargle Periodograms（LSP）譜變換可以反演得到海平面高度，并利用下列準則進行有效測高的判斷：（1）LSP頻譜的最大幅度高于20 V（1 s的采樣數據）；（2）LSP頻譜的最大幅度高于2倍平均背景噪聲；（3）LSP頻譜的至少有10個以上的峰值；（4）LPS頻譜的最大幅度高于第二峰值幅度的2倍；若LSP譜變換不滿足以上條件，將根據圖2的流程重新進行信噪比序列的選擇。

圖6分別表示碼段編號為PRN 5和PRN16兩顆GPS衛星進行LSP頻譜變換后反演的接收機天線距離海平面高度h的情況；圖中紅色直線表示平均背景噪聲，藍色曲線表示LSP頻譜；其中，碼段編號為PRN的5衛星所獲取得到的接收機天線距離海平面高度h為2.922 8 m，平均背景噪聲為3.733 9 V，碼段編號為PRN 16的衛星所獲取得到的接收機天線距離海平面高度h為3.034 7 m，平均背景噪聲為3.629 4 V，需要指出的是根據這兩顆衛星SNR序列所得到接收機天線距離海平面高度是在不同時刻的結果。

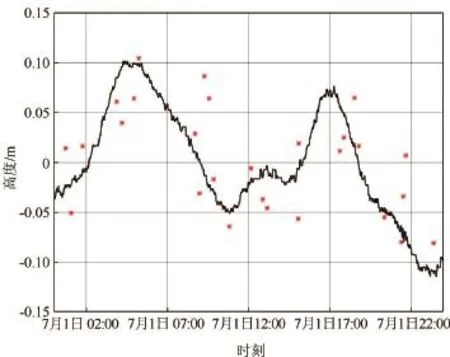
圖7 驗潮儀與GPS高度計海平面高度變化對比情況

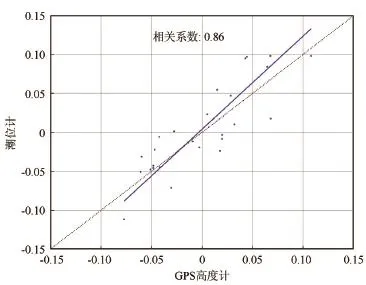
圖8 驗潮儀與GPS高度計測量結果的相關情況

根據不同衛星在24 h內的不同時間段所反演的接收機天線距離海平面高度情況，將高度變化與驗潮儀所測量的結果進行對比（見圖7）。其中，圖中的紅色星號為GPS高度計所獲取的海平面高度變化情況，黑色曲線為驗潮儀獲取的海平面高度變化情況。圖8表示驗潮儀和GPS高度計測量結果的相關情況。需要說明的是:由于GPS所測量的海平面高度是接收機天線相位中心到海平面的高度，驗潮儀所測量的是海平面高度對于所設定基準點的相對變化，兩者參考基準點不同，因此在GPS高度計測量結果與驗潮儀比較時，將GPS高度計和驗潮儀所測得的海平面高度減去各自的平均值后所得到的序列作為各自的海平面高度變化。

所進行的24 h實驗所獲得的GPS高度計海平面高度變化與驗潮儀所測得海平面高度變化的均方根誤差RMS為0.0413 m，即4.13 cm，GPS高度計與驗潮儀的測量結果相關系數為0.86。所獲得的結果與Larson等人[1]在2011年利用GPS大地測量型接收機并裝備高增益的帶球形保護罩的扼流圈天線進行海平面高度測量結果相當。實驗結果表明利用普通的接收機和天線進行海平面高度的測量也能獲得厘米級的精度。由于普通接收機和天線價格相對與大地測量型接收機便宜，未來可適合大規模應用于實際海面監測和海浪預報中。

4 結論與展望

本文建立了基于GNSS信號的海面測高數學模型，揭示了基于載波和信噪比觀測量測高方法的內在聯系；以GPS系統為例，提出了利用造價便宜的GPS接收機以及普通接收機天線進行海平面高度變化監測的手段；進行海平面高度變化監測的實驗并與驗潮儀對比分析，得到的結論如下：（1）利用普通GPS接收機和天線進行海平面高度的測量可以獲得厘米級的精度，24 h的均方根誤差為4.13 cm，GPS高度計與驗潮儀的測量結果相關系數為0.86；（2）所布設的GPS高度計與帶球形保護罩的扼流圈天線的大地測量型接收機測量結果相當，這表明該所構建的GPS高度計可以用于未來大規模實際海面監測和海浪預報中。

下一步將繼續進行GPS高度計的長時間觀測及分析，搭建基于北斗系統的海平面測高系統，實現測試站點自動化觀測預報功能，為未來大規模的沿海測高應用提供技術參考。

致謝：感謝德國地球科學中心Jens Wickert教授和上海海事大學劉衛副教授在數據分析方面的討論。

[1]Anderson K.A GPS tide gauge[J].GPS World Showcase,1995,6: 44.

[2]Cohen J,Small C,Mellinger A,et al.Estimates of coastal populations[J].Science,1997,278(5341):1209-1213.

[3]Stammer D,Ray R D,Andersen O B,et al.Accuracy assessment of global barotropic ocean tide models[J].Reviews of Geophysics, 2014,52(3):243-282.

[4]Larson K M,L?fgren J,Haas R.Coastal sea level measurements using a single geodetic GPS receiver[J].Advances in Space Research,2013,51(8):1301-1310.

[5]Zavorotny V U,Voronovich A G.Scattering of GPS signals from the ocean with wind remote sensing application[J].IEEE Transactions on Geoscience and Remote Sensing,2000,38(2):951-964.

[6]Park H,Valencia E,Camps A,et al.Delay tracking in spaceborne GNSS-R ocean altimetry[J].IEEE Geoscience and Remote Sensing Letters,2013,10(1):57-61.

[7]You H Z,Garrison J L,Heckler G,et al.The autocorrelation of waveforms generated from ocean scattered GPS signals[J].IEEE Geoscience and Remote Sensing Letters,2006,3(1):78-82.

[8]Ablain M,Cazenave A,Valladeau G,et al.A new assessment of the error budget of global mean sea level rate estimated by satellite altimetry over 1993-2008[J].Ocean Science,2009,5(2):193-201.

[9]Martin-Neira M.A pasive reflectometry and interferometry system (PARIS)application to ocean altimetry[J].ESA Journal,1993,17: 331-355.

[10]Martin-Neira M,Caparrini M,Font-Rossello J,et al.The PARIS concept:an experimental demonstration of sea surface altimetry using GPS reflected signals[J].IEEE Transactions on Geoscience and Remote Sensing,2001,39(1):142-150.

[11]Ruffini G,Soulat S,Caparrini M,et al.The Eddy Experiment: accurate GNSS-R ocean altimetry from low altitude aircraft[J]. Geophysical Research Letters,2004,31(12):L12306.

[12]Roussel N,Ramillien G,Frappart F,et al.Sea level monitoring and sea state estimate using a single geodetic receiver[J].Remote Sensing of Environment,2015,171:261-277.

[13]Roussel N,Ramillien G,Frappart F,et al.Enhancement in interference pattern technique foraltimetry and tide/wave measurements:Offshore 60-meter lighthouse case study[C]// Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium(IGARSS).Milan,Italy:IEEE, 2015:3894-3897.

[14]Bishop G J,Klobuchar J A,Doherty P H.Multipath effects on the determination of absolute ionospheric time delay from GPS signals[J].Radio Science,1985,20(3):388-396.

[15]Georgiadou P Y,Kleusberg A.On carrier signal multipath effects in relative gps positioning[J].Map Collector,1988,13(3):172-179.

[16]Gleason S,Gebre-Egziabher D.GNSS Applications and Methods [M].Boston:Artech House,2009.

[17]Carreno-Luengo H,Camps A,Ramos-Pérez I,et al.Experimental evaluation of GNSS-reflectometry altimetric precision using the p (y)and c/a signals[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2014,7(5):1493-1500.

[18]Rius A,Noqués-Correig O,Ribó S,et al.Altimetry with GNSS-R interferometry:firstproofofconceptexperiment[J].GPS Solutions,2012,16(2):231-241.

Study on sea level changes based on the observations of GPS signal to noise ratio

HU Yuan1，LIU Wei2，ZHOU Yue1，WANG Yi-jin1，YU Zi-heng1
（1.College of Engineering Science and Technology,Shanghai Ocean University,Shanghai 201306 China;2.Merchant Marine College,Shanghai Maritime University,Shanghai 201306 China）

The mathematical model of sea level altimetry based on GNSS signal carrier observables and the SNR is established,and the relation of two methods is studied in this paper.The scheme of sea level changes monitoring using inexpensive GPS receiver and off-shelf antenna is designed.Sea level monitoring experiment is conducted and the results of GPS measurement are compared with tide gauge data.The results show that centimeter accuracy of sea level changes can be archived using ordinary GPS receiver and antenna.The results of the 24 hours experiment show that the RMS error is 4.13 cm.The correlation coefficient of GPS altimeter and tide gauge measurements is 0.86.The GPS altimeter can obtain similar accuracy compared with the results of geodetic receiver equipped with a GPS antenna with a choke spherical equivalent protective cover.This indicates that the GPS altimeter can be used for future actual sea level forecasting.

GPS;signal to noise ratio;sea water level;satellite navigation

P228.4；P731.23

A

1003-0239（2017）03-0026-06

10.11737/j.issn.1003-0239.2017.03.004

2016-08-19；

2016-10-18。

國家自然科學基金（41506112,61304230）;上海教委科研創新項目（14YZ106,14YZ121）；上海海洋大學海燕計劃（A2_0209_ 14_200063）。

胡媛（1981-），女，講師，博士，主要從事衛星導航技術、GNSS-R技術以及海洋監測等研究。E-mail:y-hu@shou.edu.cn