滑動軸承承載量系數(shù)曲面擬合的高效實現(xiàn)

李玉龍， 鐘 飛， 文昌明

(成都大學 機械工程學院， 四川 成都 610106)

?

滑動軸承承載量系數(shù)曲面擬合的高效實現(xiàn)

李玉龍， 鐘 飛， 文昌明

(成都大學 機械工程學院， 四川 成都 610106)

為滿足滑動軸承優(yōu)化設(shè)計對承載量系數(shù)擬合方程之需要，結(jié)合MATLAB的擬合功能，將有限寬軸承的承載量系數(shù)的數(shù)據(jù)表，劃分為4個子數(shù)據(jù)表，針對第1個子數(shù)據(jù)表，采用擬合工具及擬合命令分別進行擬合，并就擬合誤差進行比較.結(jié)果表明：擬合工具的擬合誤差高達600%，不能用于承載量系數(shù)的曲面擬合；擬合命令的擬合誤差小于1%，符合工程實際需要；由擬合誤差中出現(xiàn)的奇異點，可有效判斷出原始數(shù)據(jù)中的錯誤之處等.所提供的3個擬合命令和擬合系數(shù)，可為滑動軸承優(yōu)化設(shè)計所直接采用，也為其他工程曲面的擬合提供一種高效的實現(xiàn)方法.

滑動軸承；承載量系數(shù)；曲面擬合；多項式系數(shù)；MATLAB

0 引 言

滑動軸承廣泛應(yīng)用于各種旋轉(zhuǎn)機械中，例如齒輪泵，其潤滑性能對旋轉(zhuǎn)機械的穩(wěn)定性、安全性以及經(jīng)濟性起著非常重要的作用[1-4].其中，承載量系數(shù)是基于雷諾方程的表征滑動軸承承載能力的一個無量綱量參數(shù)的多重積分式.由于該積分式非常困難，目前多采用數(shù)值積分的方法進行計算，并制作成相應(yīng)的線圖或表格供設(shè)計應(yīng)用[5].隨著現(xiàn)代機械向大型化、高速化方向的發(fā)展，滑動軸承的潤滑性能的分析和優(yōu)化也越來越重要[6].而在滑動軸承潤滑性能的優(yōu)化設(shè)計中，不可避免地會涉及到承載量系數(shù)的運用：一種方法是直接在優(yōu)化模型中內(nèi)嵌承載量系數(shù)的數(shù)值積分，但其效率低且計算速度慢；另一種方法是采用最小二乘法、回歸方程、NURBS曲面方程等擬合方法[7-8]，首先得到承載量系數(shù)的曲面擬合方程，然后供優(yōu)化模型調(diào)用.但這些方法的理論性相對較強，不便于工程技術(shù)人員直接采用.對此，本研究擬就承載量系數(shù)的曲面擬合的實現(xiàn)做進一步深入分析.

1 有限寬承載量系數(shù)

承載量系數(shù)是表征軸承承載能力的一個無量綱參數(shù).對于一個具體的軸承來說，在一定的外載荷作用下，軸頸將平衡在軸承中某個確定位置(一定的偏心距、一定的偏位角)，即處于穩(wěn)定工作狀態(tài).當外載荷改變時，軸頸又將遷移到新的平衡位置.所以說，承載量系數(shù)是軸頸在軸承中位置的函數(shù)，取決于軸承的包角(即入油口和出油口所包圍軸頸的夾角)、偏心率γ和寬徑比φ=B/d.其中，B為軸寬，d為軸直徑.

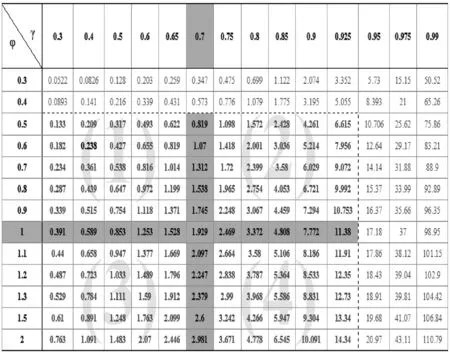
若軸承是在非承載區(qū)內(nèi)進行無壓力供油，且設(shè)液體動壓力是在軸頸與軸承襯的180 °弧內(nèi)產(chǎn)生時，則不同偏心率γ和寬徑比φ的承載量系數(shù)值如表1所示[9].同時，考慮到軸承的實際工況，將γ∈[0.3，0.925]和φ∈[0.5，2]的承載量系數(shù)值作為擬合的原始數(shù)據(jù).

表1 有限寬軸承的承載量系數(shù)表

2 原始數(shù)據(jù)的擬合分區(qū)

MATLAB作為一款用于算法開發(fā)、數(shù)據(jù)可視化、數(shù)據(jù)分析以及數(shù)值計算的計算語言和交互式環(huán)境的工具，在數(shù)值計算方面得到廣泛應(yīng)用.目前，MATLAB軟件能夠提供最高階次為5的多項曲面式擬合功能.不同階次擬合所需的原始數(shù)據(jù)點自然不同，例如，5×5多項式擬合至少需要21數(shù)據(jù)點，4×4至少需要15數(shù)據(jù)點，3×3 至少需要10數(shù)據(jù)點，2×2至少需要6數(shù)據(jù)點.

本研究擬采用5×5多項式的曲面擬合方法，為此，將表1中γ在0.3～0.925和φ在0.5～2的原始數(shù)據(jù)，以γ=0.7和φ=1作為分界點，分割為(1)、(2)、(3)、(4)的4個子表.其中，子表(1)，γ∈[0.3，0.7]和φ∈[0.5，1]；子表(2)，γ∈[0.7，0.925]和φ∈[0.5，1]；子表(3)，γ∈[0.3，0.7]和φ∈[1，2]；子表(4)，γ∈[0.7，0.925]和φ∈[1，2].那么，每一子表下的承載量系數(shù)擬合多項式，可表示為，

Cfit(φ,γ)

=p00+p10φ+p01γ+p20φ2+p11φγ+ p02γ2+p30φ3+p21φ2γ+p12φγ2+ p03γ3+p40φ4+p31φ3γ+p22φ2γ2+ p13φγ3+p04γ4+p50φ5+p41φ4γ+p32φ3γ2+ p23φ2γ3+p14φγ4+p05γ5

(1)

為便于原始數(shù)據(jù)導入MATLAB軟件中，首先將4個子表(1)、(2)、(3)、(4)中數(shù)據(jù)在Excel軟件中建立出相應(yīng)的數(shù)據(jù)表.

以子表(1)為例，其對應(yīng)的數(shù)據(jù)表如圖1所示，文件名設(shè)為Sub1.其中，A列為φ，B列為γ，C列為承載量系數(shù)的原始數(shù)據(jù)Cact.

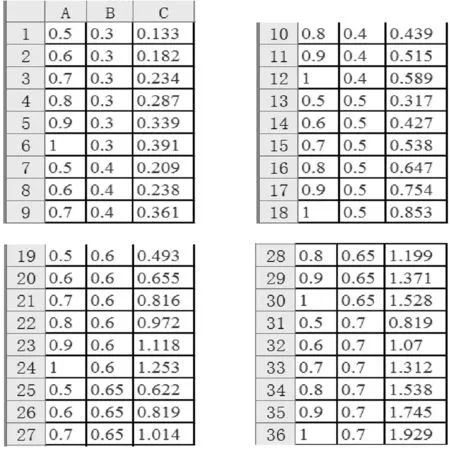
圖1 子表(1)的承載量系數(shù)Excel表

3 擬合工具的失敗擬合

在MATLAB的主頁中，依據(jù)“導入數(shù)據(jù)→Sub1→進入導入窗口→導入所選內(nèi)容→導入數(shù)據(jù)"，則生成VarName1～VarName3共3組36×1數(shù)組.在MATLAB應(yīng)用程序中，依據(jù)“CurveFitting→CurveFittingTool→VarName1(Xdata)→VarName2(Ydata)→VarName3(Zdata)→Polynomial→DegreeX：5Y：5”，則在Results窗口中顯示出對應(yīng)于95%置信度的多項式擬合方程式，其中，系數(shù)如表2所示.定義擬合誤差為，

η=(Cfit-Cact)/Cact×100%

(2)

式中，η為擬合誤差百分比；Cact為表1子表(1)中的原始數(shù)據(jù)值；Cfit為由式(1)計算出的對應(yīng)擬合值.

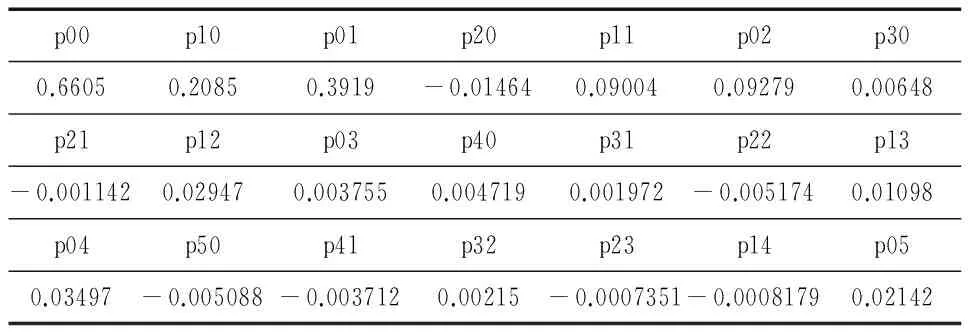
表2 子表(1)的Curve Fitting擬合多項式系數(shù)表

對應(yīng)于表1中36個原始數(shù)據(jù)下的擬合誤差，如圖2所示.結(jié)果顯示，誤差很大，說明擬合失敗.

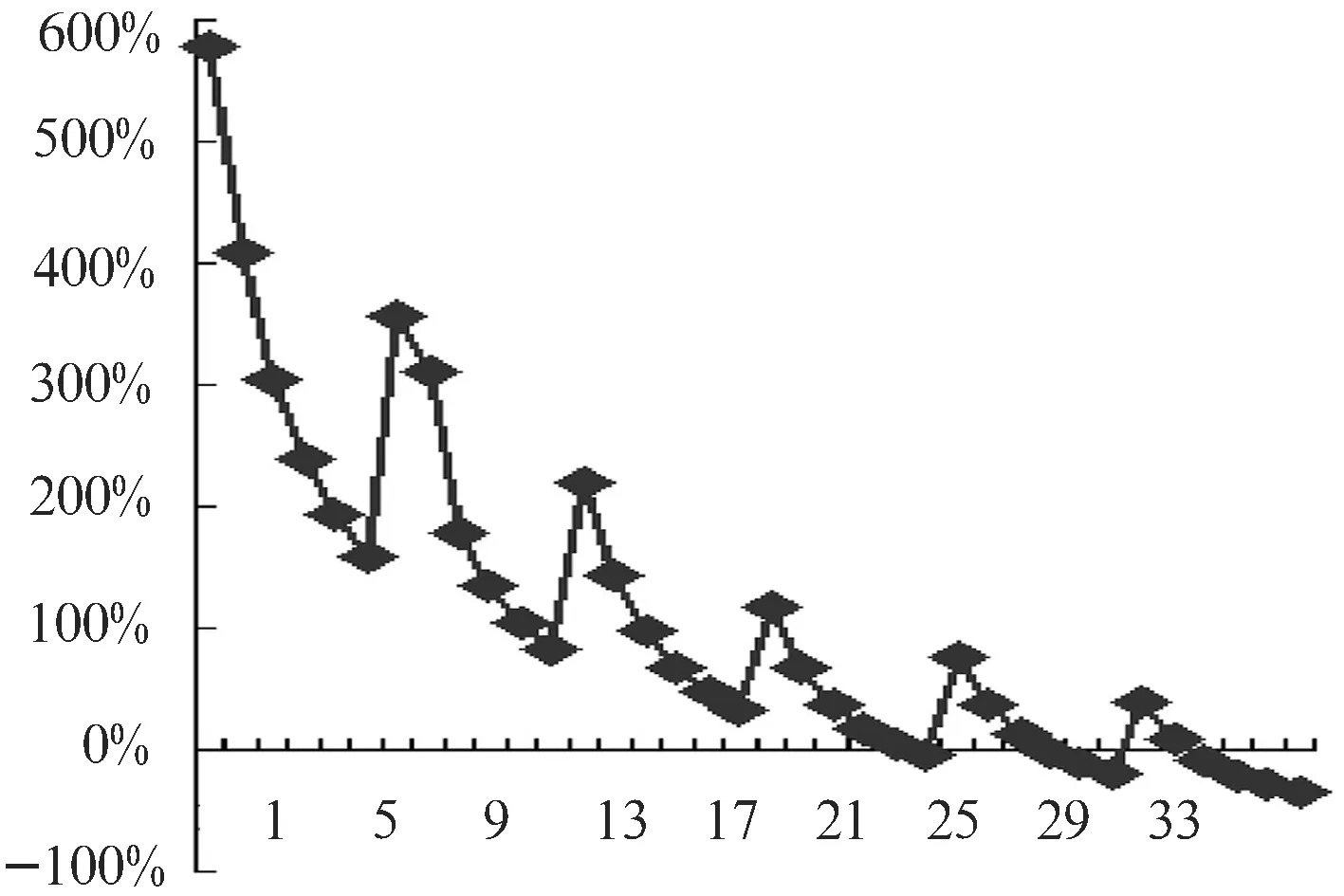
圖2FittingTool的擬合誤差率

4 擬合命令的正確擬合

由于直接采用MATLAB擬合工具不能得到正確的擬合多項式，本研究擬采用擬合命令的方式來解決該問題，具體步驟為：

首先，執(zhí)行如式(3)所示的命令語句，獲取承載量系數(shù)的多項式擬合曲面，

Poly-surface=fit([VarName1,VarName2],VarName3,′poly55′)

(3)

其次，執(zhí)行如式(4)所示的命令語句，獲取擬合多項式的系數(shù),結(jié)果如表3所示.

P=coeffvalues(Poly-surface)

(4)

最后，執(zhí)行如式(5)所示的命令語句，計算36個相應(yīng)的擬合值，其擬合誤差如圖3所示.

Cfit=feval(Poly-surface, [VarName1,VarName2])

(5)

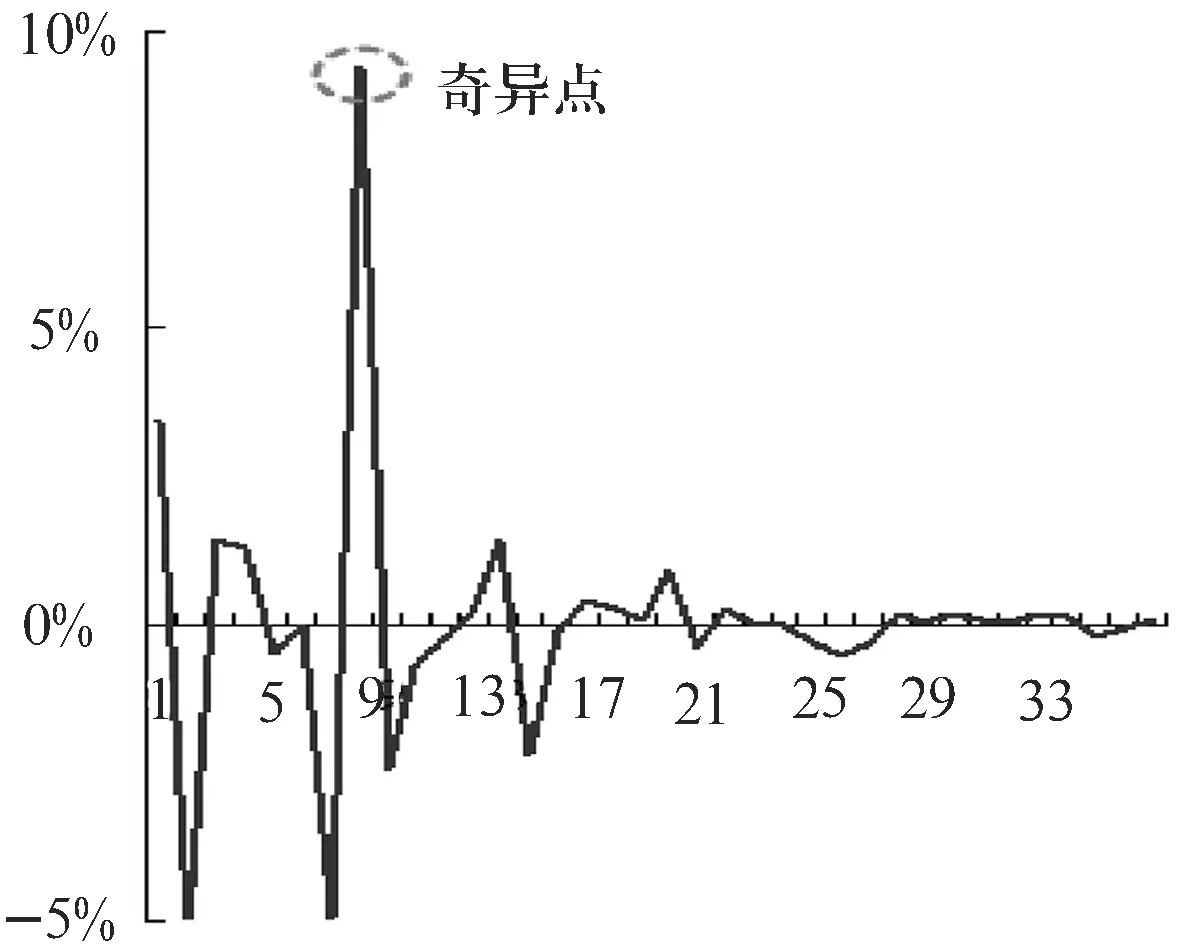
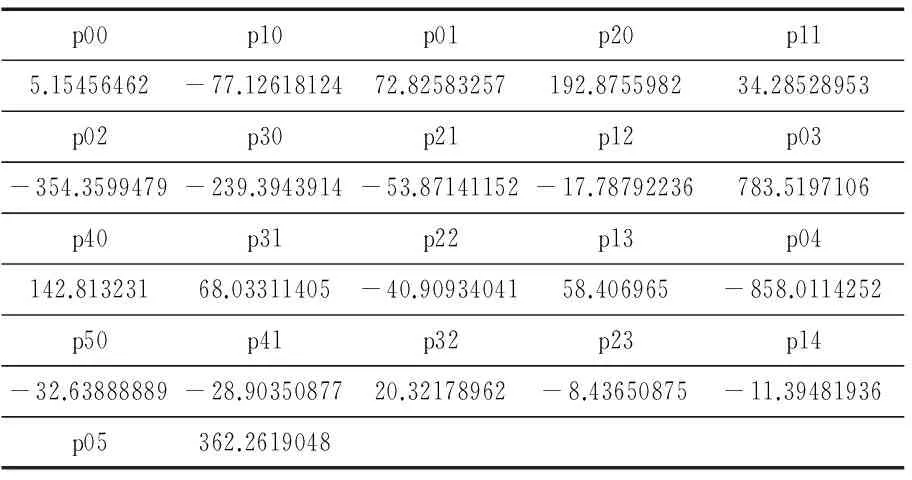
圖3 Fitting Command的擬合誤差率

從圖3可發(fā)現(xiàn)，對應(yīng)于γ=0.4、φ=0.6、Cact=0.238的擬合誤差接近10%，這與95%的擬合置信度相違背，為一奇異點.經(jīng)檢查，發(fā)現(xiàn)原始的0.238數(shù)據(jù)有誤，應(yīng)該為0.283[5].

5 承載量系數(shù)的曲面擬合

在表1中，將γ=0.4、φ=0.6時的Cact=0.238修改為0.283，并依照以上的命令擬合方式，依序執(zhí)行子表(1)～(4)多項式擬合的4組系數(shù)，結(jié)果如表4所示，承載量系數(shù)的擬合誤差如圖4所示.由表4及圖4可知，所有原始數(shù)據(jù)點的擬合誤差均小于1%，說明擬合精度相當高，完全符合工程實際需要.

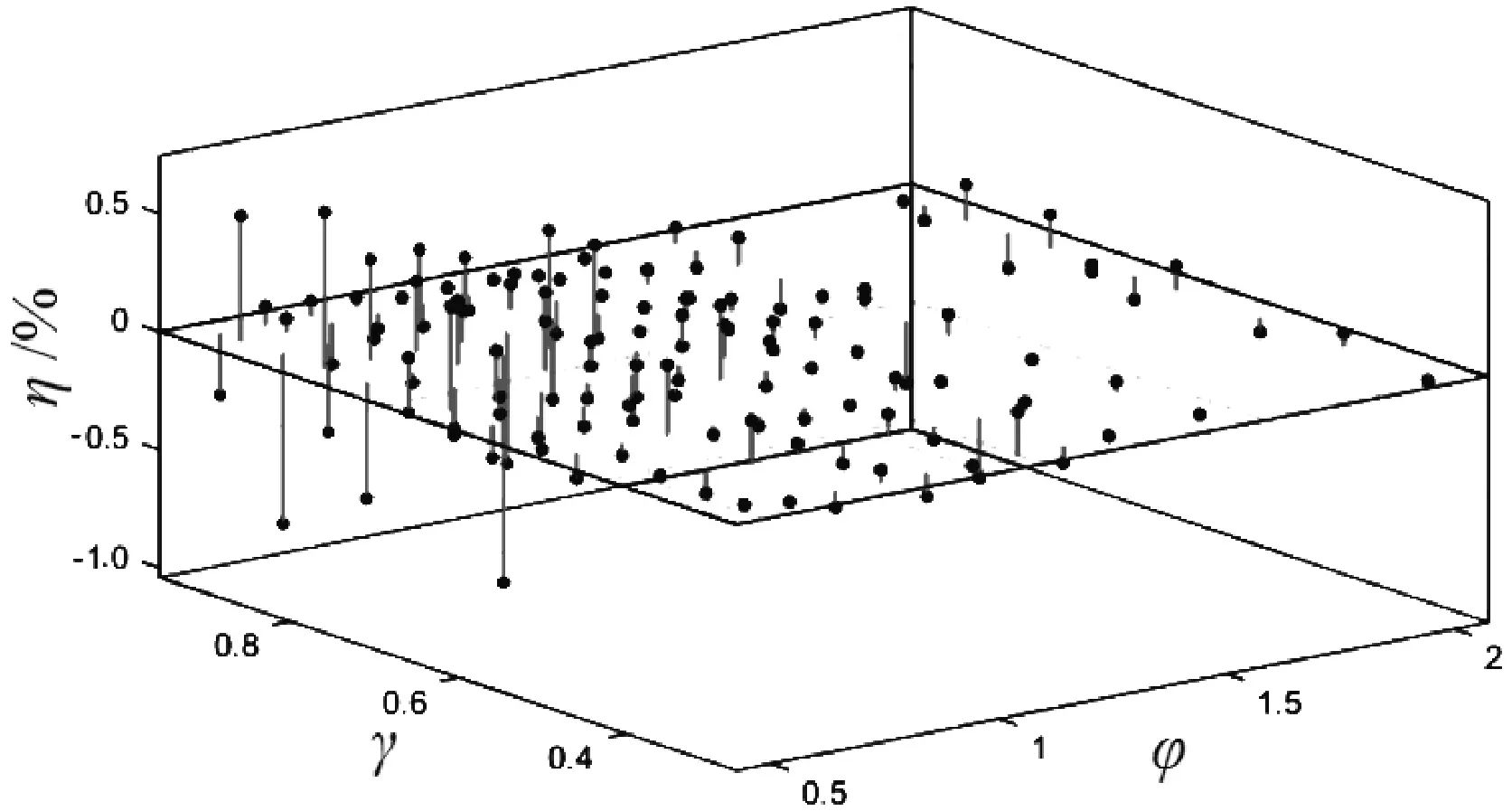
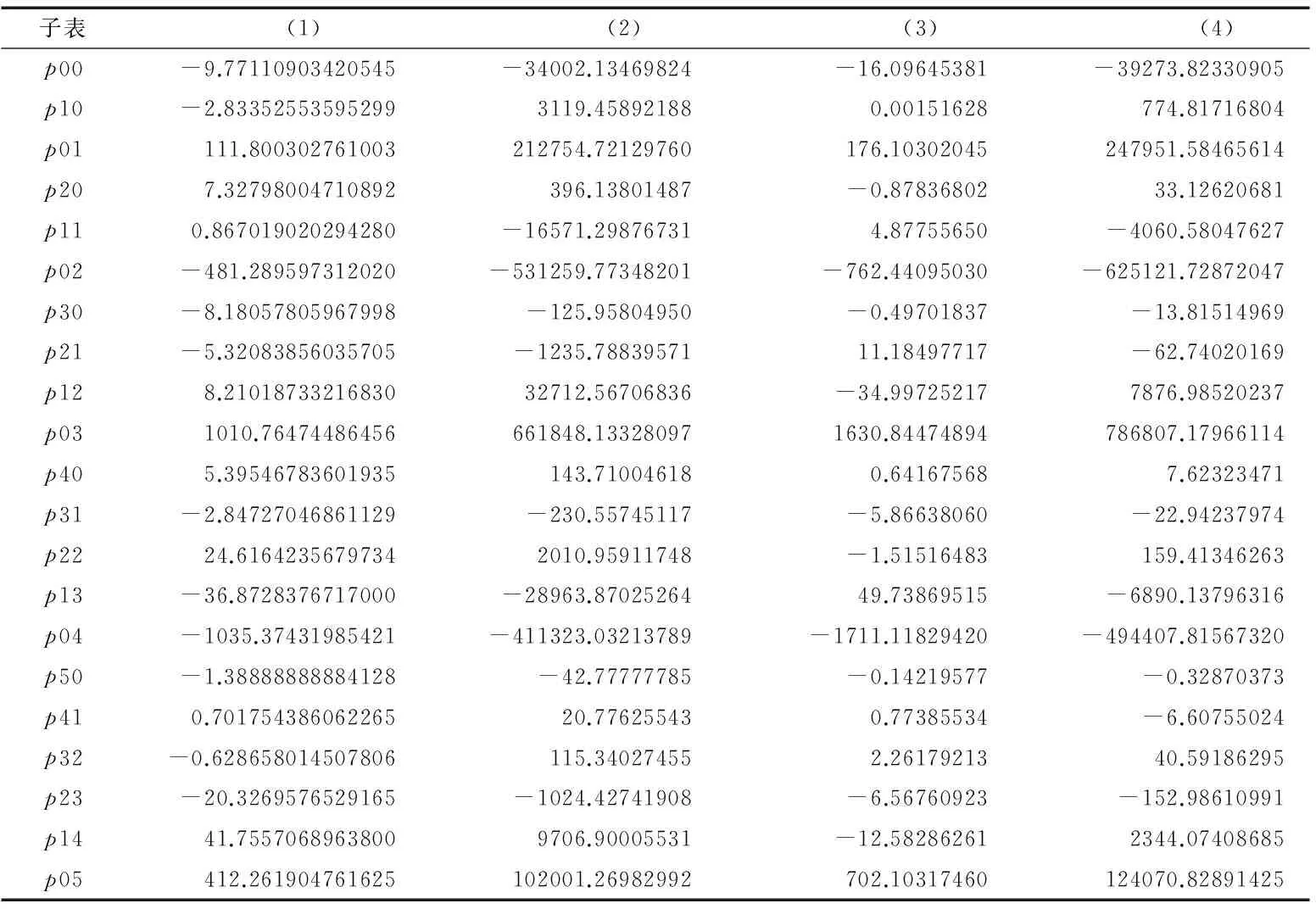
圖4 承載量系數(shù)的擬合誤差

6 結(jié) 論

采用MATLAB擬合工具的擬合誤差高達600%，不能直接用于承載量系數(shù)的曲面擬合.對此，本研究采用MATLAB擬合命令的擬合誤差小于1%，精度相當高，符合工程實際需要，同時，由擬合誤差中的奇異點，還能有效判斷出原始數(shù)據(jù)中的錯誤之處.

[1]劉維雄.滑塊軸承加速階段下潤滑性能的理論仿真與實驗研究[D].太原：中北大學，2015.

[2]米菲.活塞和曲軸軸承潤滑的數(shù)值仿真[D].哈爾濱：哈爾濱工業(yè)大學，2008.

[3]Fiebig W,Korzyb M.Vibrationanddynamicloadsinexternalgearpumps[J].Arch Civil Mech Eng,2015,15(3):680-688.

[4]何存興.液壓元件[M].北京:機械工業(yè)出版社,1982.

[5]《機械設(shè)計手冊》編委會.機械設(shè)計手冊——滑動軸承[M].北京：機械工業(yè)出版社,2007.

[6]王風斌.滑動軸承潤滑特性數(shù)值分析及優(yōu)化設(shè)計研究[D].杭州：浙江大學，2011.

[7]霍曉程,李小平.用最小二乘法擬合曲面方程[J].赤峰學院學報(自然科學版),2009,25(9):11-13.

[8]梁忠偉,馬正元,任建民.逆向工程中自由曲面測量規(guī)劃與重建研究[J].沈陽工業(yè)大學學報,2006,28(1):11-13.

[9]Liyue.徑向滑動軸承的幾何關(guān)系和承載量系數(shù)[EB/OL].[2013-09-11].http://www.iw168.cn/jixiesheji/jixiesheji/3705/.

Effective Realization of Surface Fitting of Sliding Bearing Capacity Coefficient

LIYulong,ZHONGFei,WENChangming

(School of Mechanical Engineering, Chengdu University, Chengdu 610106, China)

Fitted equation of bearing capacity coefficient is needed in the optimization design of sliding bearing.With the strong fitting function of MATLAB software，the data table of bearing capacity coefficient of the finite sliding bearing is divided into four sub-data tables. As for the first sub-data table,it is fitted by fitting tool and fitting command and then their fitting error percentage is compared.The results show that the fitting error percentage from fitting tool is as high as 600%,and thus it cann’t be used for the curved surface fitting of bearing capacity coefficient;the fitting error percentage from fitting command is as low as 1%,which is in accordance with the actual engineering demands，so it can be used for the curved surface fitting of bearing capacity coefficient;when singular points appear in fitting error percentage,the wrong data points can be effectively picked out from raw mass data.The three fitting commands and the fitting coefficient provided by sub-data tables can be directly used for sliding bearing optimization design,and provide references for a high-efficient fitting method for other curved surface fitting.

sliding bearing;bearing capacity coefficient;curved surface fitting;polynomial coefficients;MATLAB software

1004-5422(2017)02-0183-04

2017-03-19.

四川省教育廳自然科學重點課題(16ZA0382)資助項目.

李玉龍(1968 — )， 男， 博士， 教授， 從事齒輪泵理論與現(xiàn)代設(shè)計方法研究.

TH133.31

A