基于矩估計/最小二乘法的雜波模型參數估計方法

吳元偉，經富貴，2,王李波

(1.中國空空導彈研究院，河南 洛陽 471009； 2.航空制導武器航空科技重點實驗室，河南 洛陽 471009)

?

【信息科學與控制工程】

基于矩估計/最小二乘法的雜波模型參數估計方法

吳元偉1，經富貴1，2,王李波1

(1.中國空空導彈研究院，河南 洛陽 471009； 2.航空制導武器航空科技重點實驗室，河南 洛陽 471009)

針對傳統雜波模型的參數估計方法無法兼顧計算效率和精度的問題，提出了一種基于矩估計和最小二乘法的雜波統計模型混合參數估計方法，以矩估計法得到模型參數的初始值，使用最小二乘法迭代優化得到參數估計的最終值，數字仿真的結果證明了此方法的有效性和準確性；該混合模型參數估計方法可以在計算量不大、原理簡單的情況下實現模型參數的精確估計，且不局限于單一雜波模型的參數估計，具有很好的通用性和工程應用價值。

雜波分布模型；參數估計；矩估計；最小二乘法；混合估計

雜波統計模型的參數估計是雜波仿真、雷達信號處理與性能評估、目標檢測與識別的基礎[1-2]。根據雷達分辨率及地海面狀況，地海雜波的統計分析可分別用瑞利(Rayleigh)分布模型、萊斯(Rice)分布模型、對數正態(Log-normal)分布模型、威布爾(Weibull)分布模型和K分布模型等來表示[3]。對不同的模型來說，雜波分布描述的準確性取決于對模型參數估計的正確性。

目前，常用的雜波統計模型參數估計方法包括矩估計法、最大似然估計法、混合估計法等[4-11]。其中矩估計法利用各階矩的計算量與雜波幅度統計量的對比得到統計模型參數的估計值，計算方便，但精度較差；而最大似然估計是最優估計，精度高，但該方法對參數初始值敏感，且需要解高維非線性方程，計算過程復雜。常見的混合估計方法包括最大似然估計/矩估計法、矩估計/神經元網絡法。相對于單一估計法，混合估計方法可在某些方面簡化估計過程，提高計算精度，但仍然存在未解決：如最大似然估計/矩估計法無法避免求解非線性函數的問題；矩估計/神經元網絡法雖然能很好的處理噪聲問題、精度高且對初始值不敏感，但是需要較長的訓練時間，實現難度較大。

針對傳統估計方法無法兼顧計算效率和精度的問題，本文提出了一種基于矩估計/最小二乘法的雜波統計模型參數混合估計方法，即通過矩估計方法得到參數初始估值，再由最小二乘法對參數進行迭代優化得到精確的估計參數。數字仿真結果分析表明：該方法實現簡單，精度較高，具有通用性，是一種實用的雜波統計模型參數估計方法，并且不限于特定雜波模型的參數估計。

1 算法原理

對于試驗采集或仿真手段產生的雷達雜波數據，數據分析過程基于其概率密度分布的統計結果，設為p(x)。以下說明參數估計的算法流程，假設用以描述和分析數據的雜波統計模型分布的概率密度函數為f(x;a,b)，其中(a,b)為模型的兩個待估計參數。則有：

p(x) =f(x;a,b)

(1)

根據矩估計方法的原理，假設總體x的概率密度函數為x～f(x;θ1,θ2,…,θl)，θ1,θ2,…,θl為l個待估參數。若總體x的k階矩均存在，記為μk，則有：

(2)

將待分析數據作為數據總體x的樣本，設其k階矩為

(3)

由Ak=μk，在k≥l時可得到待估參數θ1,θ2,…,θl的矩估計量。矩估計方法計算簡單方便，在模型參數估計中廣泛應用。本文首先通過以上矩估計方法由式(1)得到各階矩μk與參量a,b的關系式，并與式(2)聯立形成包含k個方程的關于a,b變量的方程組，該方程的解作為雜波模型參數的值(a0,b0)。但此時計算的參數精度較差，需要進一步的優化。

將以上估計得到的參數(a0,b0)作為雜波模型參數的初始值，利用最小二乘法，控制參數的估計誤差。根據最小二乘法的原理，設

[p(x)-f(x;a0,b0)]2=min

(4)

對f(x;a,b)進行泰勒展開至一階，并由式(1)，可以得到：

(5)

對式(4)變形得到：

(6)

以差分代替上式中的微分，即

(7)

最小二乘法是通過最小化誤差的平方和找到實際數據的最佳函數匹配，可以簡便地優化估計參數。使用多元回歸的最小二乘算法，問題轉化為求解使式(7)中誤差函數最小的參數(a,b)，采用基于梯度搜索的LMS算法求解參數，即可得到(Δa,Δb)，進而得到雜波模型參數的修正值：

a1=a0+Δa;b1=b0+Δb

(8)

當誤差(Δa,Δb)不滿足閾值判斷條件時，將修正值(a1,b1)返回，繼續上述迭代優化過程，直到參數的修正值滿足設置的誤差閾值。

算法的流程圖如圖1所示。

圖1 算法流程

1) 根據試驗測量或者數字仿真的雜波數據，統計得到雜波概率密度函數p(x)；

2) 使用矩估計的方法計算數據序列的各階矩Ak，利用Ak與雜波模型的各階矩μk的關系，計算參數的初始值(a0,b0)；

3) 根據雜波模型參數現有估計值f(x;a0,b0)，得到其余實測數據分布密度函數的差值p(x)-f(x;a0,b0)以及f(x;a0,b0)對應偏微分的近似值(差分)；

4) 由最小二乘估計法的原理，結合式(7)，計算雜波模型參數的修正量(Δa,Δb)；

5) 判斷修正量是否小于閾值ξ，如果大于閾值，重復3)～5)步驟；若修正量小于閾值，即得到雜波模型參數的最終估計值(a,b)。

對于待分析的雜波數據，在事先無法確定描述其概率密度分布的最佳模型的情況下，可利用上述方法對可能的雜波模型進行擬合。最后根據計算的結果，評估各種模型與數據的匹配度，選擇出最佳的模型來描述相關數據，再進行后續的分析。

2 仿真驗證

本文以K分布雜波為例，通過數字仿真說明上述雜波參數估計算法實現過程，驗證其有效性。K 分布可以準確地描述高分辨雷達在低擦地角下回波幅度統計分布的拖尾現象，在雷達數據分析、地海雜波建模以及雷達信號檢測與識別中具有廣泛的應用，精確而快速的K分布模型參數估計方法一直是研究的熱點。

2.1 K分布雜波模型

K 分布可以看作散斑分量(快變化分量)和基本幅度調制分量(慢變化分量)兩個因子的乘積：前者表示大量散射體反射的相參疊加(服從Rayleigh分布)，后者表示與地海大面積結構相關的散射束平均功率(服從Gamma分布)，其概率密度函數為

(9)

其中， Γ(ν)為伽馬函數，Kν-1為ν階第二類修正貝塞爾函數，α為尺度參數，與雜波的強度相關，ν為形狀參數。典型條件下K分布的概率密度函數如圖2所示，由圖2中可以發現由于概率密度積分的固定為1，因此ν越大，K分布的峰位越偏大，相同α條件下導致K分布越平緩，拖尾現象更明顯；而α越大，幅度大雜波變多，相同ν條件下K分布越平緩。

使用矩估計方法，可以得到參數估計值為

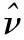
=(E(x4)/2E2(x2)-1)-1

(10)

(11)

其中E(x4)與E(x2)分別為K分布的四階矩/二階矩樣本的數量影響估值的精度。

2.2 仿真數據驗證

為驗證矩估計/最小二乘法混合估計算法，通過球不變隨機過程法仿真得到了一組K分布雜波數據，其實部與虛部的數據如圖3所示。

圖2 典型的K分布概率密度函數

圖3 K分布雜波數據

圖4 雜波數據的概率密度函數與功率譜密度

根據算法流程，統計得到雜波概率密度函數p(x)如圖4所示，并計算雜波數據的四階矩/二階矩。用矩估計方法根據式(10)、式(11)得到K分布參數估計初始值(v0,α0)，按照本文混合估計方法的算法流程計算參數的估計值。設最小二乘法中誤差的判斷閾值為0.02，仿真過程中χ2隨迭代次數變化情況如圖5所示，從結果上看，本文提出的方法經過8次迭代就實現了數據收斂，計算的效率較高。

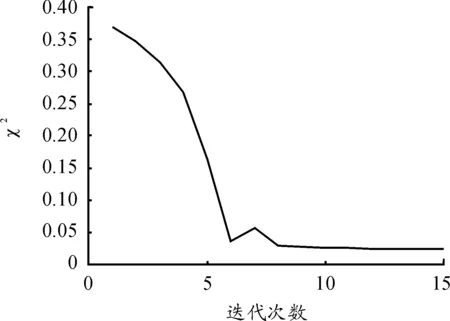
圖5 χ2隨迭代次數的變化

圖6中虛線為矩估計方法得到的概率密度分布函數，與雜波數據的統計結果偏差較大；雙劃線為混合估計方法得到的概率密度分布函數，從中可以發現混合估計方法對雜波模型的參數進行了優化，使其能夠準確地描述原始數據的統計結果。

圖6 不同估計方法得到的概率密度函數

3 結論

雜波統計模型的參數估計方法對雜波研究非常重要，本文提出了一種基于矩估計和最小二乘法的雜波統計模型混合參數估計方法，以矩估計法得到模型參數估計初始值，使用最小二乘法得到參數估計的修正量，通過迭代方法得到參數估計的最終值，在計算量不大、原理簡單的情況下實現了參數的精確估計。數字仿真數據的分析證明了本文提出的混合估計方法的有效性和準確性，本方法不局限于單一雜波模型的參數估計，具有很好的通用性。

[1] 司文濤,童寧寧,王強.海雜波背景中小目標檢測算法研究[J].信號處理,2014,30(1):106-111.

[2] 馬國哲,任麗莉,曹旭東.復雜波形體制下雷達導引頭地雜波分析[J].航空兵器,2011(1):38-42.[3] 斯科爾尼克.M.I.雷達手冊[M].北京：國防工業出版社,1978.

[4] 石志廣,周劍雄,付強.K分布海雜波參數估計方法研究[J].信號處理,2007,23(3):420-424.

[5] 徐偉,陳永森.一種K分布雜波參數估計方法[J].艦船電子對抗,2013,36(3):82-84.

[6] 蘇昭斌,陳紅衛.海雜波復合K分布模型的參數估計[J].計算機應用與軟件,2014,31(8):273-275.

[7] 任雙橋,劉永祥,黎湘,等.廣義K分布雜波模型參數估計[J].電子學報,2006,34(12):2278-2281.

[8] 朱人杰,陳紅衛.基于遺傳算法的海雜波K分布參數估計[J].艦船科學技術,2014(10):115-118.

[9] 劉川何.求解分裂可行問題的一種松弛投影算法[J].重慶工商大學學報(自然科學版)，2016,33(1):16-18.

[10]余慧,王巖飛,閆鴻慧.一種K分布雜波參數估計的快速算法[J].電子與信息學報,2009,31(1):139-142.

[11]鑒福升,曾浩.實測海雜波數據的統計擬合優度分析[J].雷達科學與技術,2013,11(3):276-280.

(責任編輯 楊繼森)

A Hybrid-Estimation Method of Clutter Distribution Models Based on MOM and Least Square Method

WU Yuan-wei1， JING Fu-gui1,2， WANG Li-bo1

(1. China Airborne Missile Academy, Luoyang 471009, China;2.Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons, Luoyang 471009, China)

The traditional parameter estimation methods of clutter distribution models can’t balance the calculation efficiency and accuracy. To solve this problem, a generalized hybrid-estimation method based on MOM(method of moments)and least square method is presented. MOM is utilized to obtain the initial values of model parameters, which are iteratively optimized with least square method. The simulation results confirm the validity and accuracy of the method. The hybrid method realizes the accurate estimation of clutter parameters with little computational cost, and is not confined to the parameter estimation of any particular clutter model. It can be generally used in engineering application.

clutter distribution models; parameter estimation; MOM; least square method; hybrid-estimation

2017-02-11；

2017-03-10

交叉眼干擾與抗干擾技術研究基金資助項目(2014C01407R)

吳元偉(1989—),男,碩士研究生,助理工程師,主要從事雷達目標與環境特性研究。

10.11809/scbgxb2017.06.021

format:WU Yuan-wei，JING Fu-gui，WANG Li-bo.A Hybrid-Estimation Method of Clutter Distribution Models Based on MOM and Least Square Method[J].Journal of Ordnance Equipment Engineering,2017(6):95-98.

TN957；TJ765

A

2096-2304(2017)06-0095-04

本文引用格式：吳元偉，經富貴,王李波.基于矩估計/最小二乘法的雜波模型參數估計方法[J].兵器裝備工程學報，2017(6):95-98.