近海油料輸轉系統管線排空模型及數值模擬

陳 暢,張 帆，張世富,張起欣

(后勤工程學院 a.軍事油料應用與管理工程系; b.機械電氣工程系; c.國家救災應急裝備工程技術研究中心; d.軍事供油工程系, 重慶 401311)

?

【后勤保障與裝備管理】

近海油料輸轉系統管線排空模型及數值模擬

陳 暢a,張 帆b，張世富c,張起欣d

(后勤工程學院 a.軍事油料應用與管理工程系; b.機械電氣工程系; c.國家救災應急裝備工程技術研究中心; d.軍事供油工程系, 重慶 401311)

針對近海油料輸轉系統管線排空作業，建立了管線排空數學模型，運用MATLAB軟件，計算了在不同工作壓力情況下，管線總的排空時間；分析了在不同時間間隔下，管線受到的摩擦阻力和速度分布情況；運用ANSYS軟件，構建了管線排空數值模型，分析了管線壓力分布、速度分布以及流體軌跡分布規律，對掌握管線排空作業過程中的力學規律具有指導意義。

近海油料輸轉系統；管線排空；數值模擬；ANSYS；MATLAB

軟質管線因其較大的抗拉強度和較小的抗彎剛度，具有儲存空間小和便于收展的特點，廣泛應用于近海油料輸轉和其他海洋工程領域。在近海進行油料輸轉作業后，為了實現管線快速撤收，必須先對管線實施排空作業。有關學者對管線排空進行了相關研究。甘文瀟等[1]對目前采用的自流排空、水頂法排空、氣頂法排空等工藝技術特點，進行了分析比較。吳秀全等[2]針對注汽鍋爐冬季點停爐排空管線凍堵問題，提出了解決對策并進行了改進。劉忠輝等[3]對聚酯裝置漿料配制罐排空管線的堵塞原因進行了分析。姜俊澤等[4]根據鋼質機動管線的結構特點，設計制作了雙絲電容探針持液率檢測裝置，并用該裝置對排空過程中管內的持液率進行了實測。程雪[6]針對油庫及管線系統油污水具有不連續性、油水密度差較大、含油污水中含油量較低、懸浮物較少的情況,研制了采用聚結分離技術的污水處理裝置。李正陽等[7]通過對機動管線水頂油排空作業終端混油切割流程、設備操作的分析,測量了三通球閥的流動特性,論證了三通球閥作為機動管線混油切割閥的可行性。從目前文獻檢索的情況看，對管線排空方面的研究較少，尤其是對管線排空的模型化分析和數值分析還未見報道。本文從工藝的角度出發，結合作業實際，構建了海上軟質管線排空模型，并進行了數值分析，對于分析管線排空過程規律有一定的意義。

1 管線排空工藝流程

在完成近海油料輸轉后，對管線進行快速撤收前，必須對海上軟質管線排空，由于所有都依托船載設備，必須在作業船設置排空單元，以實現對管線排空作業。排空單元可由空壓機、高壓儲氣罐、收發球裝置、高壓彈簧氣卷盤等組成，主要完成管線壓力試驗、氣頂排空和收發清管球作業。排空工藝流程如圖1所示。

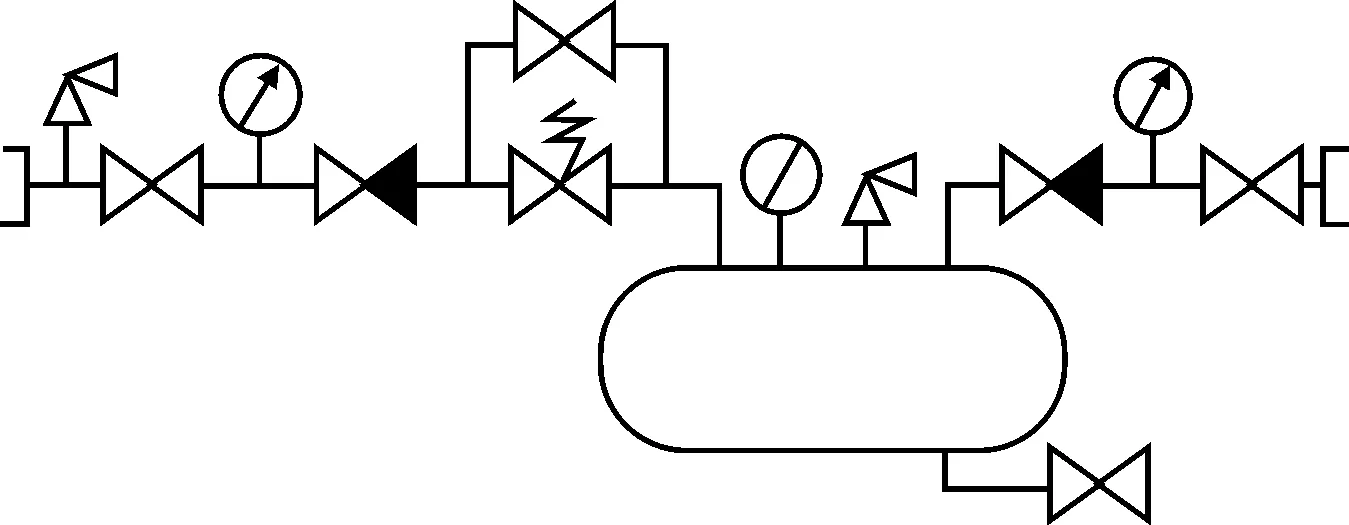
圖1 排空工藝流程

2 管線排空模型

根據管線排空的實際情況，建立管道排空模型[5]，排空模型示意圖如圖2。

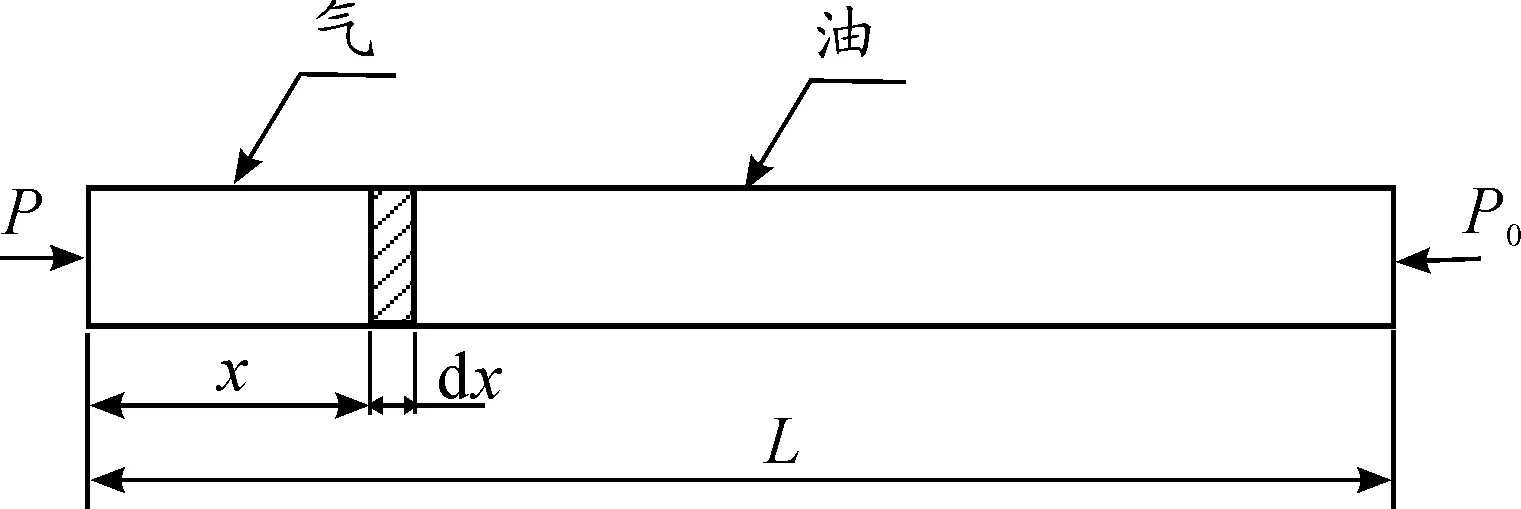
圖2 排空模型示意圖

在t時刻氣液混合面到達圖 2中所示的位置，即混合面距離進口距離為x，經過dt時刻向出口方向移動了dx的距離。

由普朗特公式結合雷諾數公式，可得

(1)

式(1)中λ為t時刻液體段的摩阻因數，Re為t時刻液體段的雷諾數，v為t時刻液體段的運動速度，υ為輸送液體的運動黏度。

以t時刻管道剩余的液體為對象，分析該段液體的受力情況：該段液體受到氣液混合面向出口方向的壓力P，受到管道出口處的壓力P0，同時受到摩擦阻力f，由牛頓定律可得：

(2)

式(2)中S為管道斷面積，ft為t時刻液體段受到的摩擦力，mt為t時刻液體段的質量，at為t時刻液體段的運動加速度，γ為輸送液體的重度。

由沿程摩阻損失公式得：

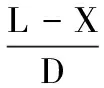
(3)

根據牛頓內摩擦定律得：

(4)

式(4)中τ為管道界面上的平均切應力，i為管道的能坡度，hw為總水頭損失，hf為沿程摩阻損失，hj為局部摩阻損失，K為比例系數。

將式(1)至式(4)聯立可得：

(5)

3 管線排空數值模擬

1) 幾何模型建立。根據氣頂排空的作業方式，系統為裝備補給完油料之后，在空壓機的作用下，將空氣注入管道內部，推動清管器向前運動，清管器推動管道內的余油排出管道。考慮到該模型是氣液混合模型，因此采用二維平面氣液混合VOF模型，即輸油管道軸向斷面，如圖3所示。

2) 網格劃分。由于采用二維平面模型，且模型為矩形，因此本文采用平面掃略(sweep)矩形網格劃分的方式，設置左端為模型出口(outlet)，右端為模型入口(inlet)，網格數量為30 354，節點數為4 560個，如圖4所示。

圖3 管道排空模型

圖4 管道排空模型網格劃分

3) 控制方程。其方程如下：

① 連續方程

用積分形式表示系統的質量，可得：

m=?V(t)ρdV

(6)

按照質量守恒定理，用數學方法表示，即

(7)

式(7)為連續方程的拉格朗日積分形式，結合輸運方程和高斯公式，可以得到歐拉形式的連續方程，即

+▽·(ρu)=0

(8)

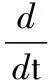
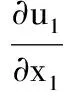
(9)

② 動量方程

運動的流體微元的動量可以表示為

udm=ρudV

(10)

動量守恒原理是流體系統的動量變化率等于系統受外力之和，即

?V(t)ρdV=∑F

(11)

式(11)中外力F主要包括體積力(質量力)和面積力，結合應力的張量形式、雷諾第二輸運方程、高斯公式等，簡化后的動量方程為

(12)

③ 能量方程

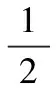
(13)

式中∑W為單位時間內外力對系統作功之和，∑Q為單位時間傳入系統的全部熱量。

4) 求解器與參數設置。選擇二維單精度基于壓力的瞬態VOF(Volume of Fluid) 模型，粘度方程選擇k-ε求解器方程；近壁面采用標準壁面函數的處理方法，選擇空氣(air)和柴油(diesel-liquid)作為研究的介質；選擇階段1為空氣，階段2為柴油；在邊界條件的設置中，選擇壓力入口(Pressure Inlet)，壓力出口(Pressure Outlet)；在求解方法的設置中，選擇SIMPLEC的壓強速度關聯形式，設置適當的松弛因子以及計算精度，選擇恰當的時間步長、反饋時間和迭代次數，進行迭代計算。

4 結果與分析

4.1 管線排空模型計算

式(5)可以整理成關于dx和dt的微分方程，按總長度L=1 350 m，管線內徑d=98 mm，利用Matlab軟件進行計算機編程，計算壓縮機工作壓力分別為：3.0 MPa、1.0 MPa、0.7 MPa情況下的排空總時間T，求解結果如表1所示。

表1 利用Matlab編程得到排空時間結果

運用Matlab編程，計算在不同時間間隔下，管道受到的摩擦阻力和速度分布情況，如圖5、圖6所示。

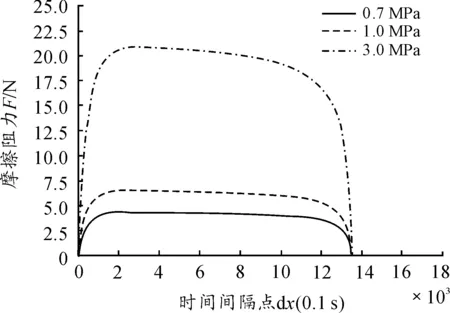
圖5 摩擦阻力隨排空時間變化情況

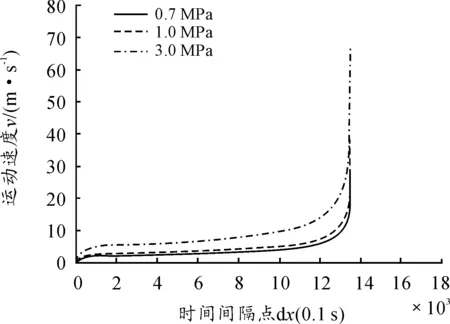
圖6 速度大小隨排空時間變化情況

從圖5、圖6可知：摩擦阻力隨著排空時間，開始急速增大到某個值，隨后以十分緩慢的速度減小，到了某個時間點急速降低至基本為零；排空速度的大小從零開始隨時間增大而逐漸增大，當接近排空末端時，速度急劇增大。這主要是由于排空剛開始階段管道內充滿液體，其摩擦阻力較大，排空速度較慢，隨著排空任務的進行，氣體段體積逐漸增大，液體段體積逐漸減小，摩擦阻力不斷減小，排空速度逐漸增大，當液體段全部排空時，管道內充滿了氣體，阻力基本為零，排空速度達到最大值。

4.2 數值模擬結果分析

1) 壓力分布規律。由迭代計算可以得到，管道排空時的壓力變化云圖，如圖7。

圖7 管道排空壓力云圖

從圖7可知：在進行排空任務時，與空壓機高壓儲氣罐出口相連接處的壓力較高，沿著排空方向靜壓力不斷減小，在出口處靜壓力最小；這是由于隨著排空的進行，空氣段摩擦阻力較小，柴油段摩擦阻力較大。在考慮管道的承壓能力以及承壓安全時，主要對排氣入口端的關鍵點進行排查。

2) 速度分布規律。通過迭代計算，得到排空管線速度分布矢量圖，如圖8。從圖8可知：沿著管道排空方向，內部流體的運動速度逐漸加大；從徑向進行比較，排氣入口處存在最小值，出口處存在最大值；這是由于空氣段的摩擦阻力較小，柴油段的摩擦阻力較大，隨著時間的推移，整段管道的摩擦阻力不斷減小，因此排空速度沿著排空方向不斷增大；同時由于管道近壁面處存在邊界層，因此靠近管道壁面的速度小，管道內部的速度大。

圖8 速度分布矢量圖

③ 流體粒子軌跡分布規律

通過迭代計算，得到內部流體的軌跡分布圖，如圖9所示。

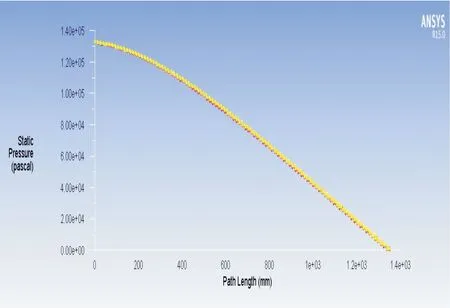
圖9 流體軌跡與靜壓力的關系

從圖9可知，在排空過程中，內部流體主要包括空氣和柴油以及二者氣液混合體，在進口段其壓力為最大值，即為壓縮機所能提供的最大壓力，隨著運動的進行，其靜壓力不斷減小，最終在出口處達到最小值。

5 結論

本文對軟質管線排空作業進行分析，建立了管線排空數學模型，結合實際情況計算出壓縮機工作壓力在3.0 MPa情況下，總的排空時間為194.58 s，分析了不同時間間隔下，管道受到的摩擦阻力和速度分布情況。運用ANSYS軟件，構建了軟管模型，分析了壓力分布、速度分布以及流體粒子軌跡分布規律，對檢測管道的承壓能力以及承壓安全具有指導意義。

[1] 甘文瀟,江崇林,劉佩,等.長江中上游浮動碼頭液態危化品管線排空工藝技術探討[J].中國儲運,2014(3):135-136.

[2] 吳秀全,申長云,鄭強,等.注汽鍋爐冬季點停爐排空管線凍堵問題探討[J].新疆石油科技,2015(1):73-74.

[3] 劉忠輝,張國躍,閔宇.聚酯裝置漿料配制罐排空管線堵塞原因分析[J].設備管理與維修,2013(3):64.

[4] 姜俊澤,張偉明,雍歧衛,等.機動管線氣頂排空過程持液率特性的實驗研究[J].實驗流體力學,2016(4):48-55.

[5] 姜俊澤，張偉明，段紀淼，等. 野戰輸油管線排空過程的氣體與液體兩相流瞬態模型[J]兵工學報，2016(8):1536-1542.

[6] 程雪.長輸管線試壓及排空污水的除油原理與處理裝置研究[D].北京：北京化工大學,2013.

[7] 李正陽,張偉明,賈鄧樂,等.機動管線水頂油排空油水混合物切割工藝研究[J].后勤工程學院學報,2013(6):30-35.

(責任編輯 唐定國)

Model and Numerical Simulation for Pipeline Evacuation of Offshore Oil Transportation System

CHEN Changa, ZHANG Fanb, ZHANG Shi-fuc, ZHANG Qi-xind

(a.Department of Military Oil Application and Management Engineering; b.Department of Mechanic and Electric Engineering; c.National Engineering Research Center for Disaster and Emergency Relief Equipment; d.Department of Petroleum Supply Engineering, Logistic Engineering University, Chongqing 401311, China)

This paper focuses on the pipeline evacuation of offshore oil transportation system. The mathematical model for pipeline evacuation was established, and the total emptying time under different working pressure was calculated by using MATLAB software. Frictional resistance and velocity distribution of the pipe under different time intervals was analyzed. The numerical simulation for the pipeline evacuation was carried out by using ANSYS software. The pressure distribution, velocity distribution and distribution law of the fluid trajectory are analyzed, which will make contribution to the analysis and control of the variation of the pipeline during the evacuation operation.

offshore oil transportation system; pipeline evacuation; numerical simulation; ANSYS; MATLAB

2017-01-25；

2017-02-26

軍需能源專業科研項目(YX213Z044)

陳暢(1990—)，男，博士研究生，主要從事油氣加注技術與裝備、油料勤務研究。

10.11809/scbgxb2017.06.017

format:CHEN Chang, ZHANG Fan, ZHANG Shi-fu, et al.Model and Numerical Simulation for Pipeline Evacuation of Offshore Oil Transportation System[J].Journal of Ordnance Equipment Engineering,2017(6):76-79.

TE97

A

2096-2304(2017)06-0076-04

本文引用格式：陳暢,張帆，張世富，等.近海油料輸轉系統管線排空模型及數值模擬[J].兵器裝備工程學報，2017(6):76-79.