一種復(fù)雜機(jī)電系統(tǒng)LE-SVDD異常監(jiān)測方法

亞森江·加入拉， 高建民， 高智勇， 姜洪權(quán)， 陳子勝

(1.西安交通大學(xué)機(jī)械制造系統(tǒng)工程國家重點(diǎn)實驗室 西安，710049)(2.新疆大學(xué)機(jī)械工程學(xué)院 烏魯木齊，830046)

?

一種復(fù)雜機(jī)電系統(tǒng)LE-SVDD異常監(jiān)測方法

亞森江·加入拉1，2， 高建民1， 高智勇1， 姜洪權(quán)1， 陳子勝1

(1.西安交通大學(xué)機(jī)械制造系統(tǒng)工程國家重點(diǎn)實驗室 西安，710049)(2.新疆大學(xué)機(jī)械工程學(xué)院 烏魯木齊，830046)

復(fù)雜機(jī)電系統(tǒng)生產(chǎn)過程監(jiān)測數(shù)據(jù)具有明顯的高維非線性和復(fù)雜分布特點(diǎn)，針對傳統(tǒng)的方法難以滿足復(fù)雜系統(tǒng)異常辨識的要求，提出一種拉普拉斯特征映射-支持向量數(shù)據(jù)描述(Laplacian eigenmaps-support vector domain description，簡稱LE-SVDD)的異常監(jiān)測方法。由于高維特征空間中距離很近的點(diǎn)投影到低維空間后距離應(yīng)該很近，因此改進(jìn)的LE方法使用一個有權(quán)無向圖來描述一個流行，用嵌入的方式找到高維數(shù)據(jù)的低維嵌入，從而能夠發(fā)現(xiàn)高維數(shù)據(jù)內(nèi)部的地位流行結(jié)構(gòu)。通過標(biāo)準(zhǔn)的田納西-伊斯曼過程(Tennessee Eastman process，簡稱TE過程)測試和訓(xùn)練數(shù)據(jù)進(jìn)行仿真實驗，給出了在非線性特征提取和不同時段異常辨識的準(zhǔn)確結(jié)果。平均漏報率和誤報率都比較低，分別為6.063，6和5.625，3.125，這表明LE-SVDD方法在狀態(tài)監(jiān)測中具有良好的非線性和高維數(shù)據(jù)處理能力，適用于工程系統(tǒng)的監(jiān)測診斷。

復(fù)雜機(jī)電系統(tǒng)； 異常監(jiān)測方法； 特征提取； 拉普拉斯特征映射-支持向量數(shù)據(jù)描述(LE-SVDD)； 田納西-伊斯曼(TE)過程

引 言

化工生產(chǎn)系統(tǒng)是有諸多大型機(jī)電和化工設(shè)備組成的龐大且分布式復(fù)雜系統(tǒng)，是典型的流程工業(yè)系統(tǒng)。對生產(chǎn)過程狀態(tài)有效地進(jìn)行監(jiān)測并及時排除故障因素是保證企業(yè)安全生產(chǎn)、提高產(chǎn)品質(zhì)量和經(jīng)濟(jì)效益的重要手段。在復(fù)雜機(jī)電系統(tǒng)這一特殊的設(shè)備群中，使用一種有用而合適的狀態(tài)監(jiān)測方法具有非常重要的研究意義。

國內(nèi)外學(xué)者提出的狀態(tài)監(jiān)測方法很多。Frank以先驗知識為基礎(chǔ)，將故障診斷方法分為三大類，分別為基于解析模型、基于專家知識的定性分析方法以及基于數(shù)據(jù)驅(qū)動的分析方法[1]，但是針對的都是特定的問題，未能考慮到系統(tǒng)的復(fù)雜性特性。對于復(fù)雜機(jī)電系統(tǒng)，由于難以建立準(zhǔn)確的數(shù)學(xué)模型，因此限制了基于模型的監(jiān)測診斷方法的應(yīng)用。在理論上，目前數(shù)據(jù)挖掘理論逐漸成熟，神經(jīng)網(wǎng)絡(luò)、支持向量機(jī)、一致性預(yù)測與支持向量隨機(jī)描述等方法逐漸在故障診斷領(lǐng)域被應(yīng)用[2-4]。文獻(xiàn)[5]提出了基于SVDD的機(jī)械故障的單分類新方法。如果目標(biāo)分類是有效的，該方法在離群值類未知情況下能夠區(qū)別離群值對象和目標(biāo)對象。文獻(xiàn)[6]對凝汽器結(jié)污(condenser fouling,簡稱CdF)和制冷劑泄漏(refrigerant leakage，簡稱RfL)兩種故障情況提出了主成分分析-殘渣-支持向量數(shù)據(jù)描述(principal component analysis-residual-support vector domain description，簡稱PCA-R-SVDD)基礎(chǔ)模型。與傳統(tǒng)的方法相比較，提出的方法具有更好的故障數(shù)據(jù)分布和更嚴(yán)格的統(tǒng)計檢測能力。其他相關(guān)的研究成果同樣采用基于改進(jìn)的SVDD方法，由于使用領(lǐng)域和設(shè)備不同，因此改進(jìn)的優(yōu)化方法也有所不同[7-10]。雖然這些方法充分考慮了非線性因素并較好地解決了因相關(guān)性造成的信息冗余，但是針對的是單臺設(shè)備或較簡單的工業(yè)過程，未能充分考慮到流程工業(yè)系統(tǒng)的復(fù)雜性特性。

復(fù)雜機(jī)電系統(tǒng)生產(chǎn)過程監(jiān)測數(shù)據(jù)具有明顯的高維非線性和分布復(fù)雜的特點(diǎn)，因此傳統(tǒng)的線性方法PCA和基于高斯分布假設(shè)核主元分析方法(kernel principal component analysis，簡稱KPCA)的故障監(jiān)測方法難以滿足復(fù)雜機(jī)電系統(tǒng)異常狀態(tài)監(jiān)測的要求。雖然KPCA能夠有效提取原始數(shù)據(jù)的非線性特征，但是核方法處理效果的好壞一方面依賴于核函數(shù)的類型，另一方面受核參數(shù)的影響。核函數(shù)通常選取常用的幾類核函數(shù)形式，核參數(shù)的選取無科學(xué)的理論指導(dǎo)，目前尚未出現(xiàn)有效的解決方法。

為了適應(yīng)復(fù)雜機(jī)電系統(tǒng)模式的復(fù)雜性和多樣性，解決非高斯分布樣本的異常監(jiān)測問題，筆者提出一種基于特征樣本建模的復(fù)雜機(jī)電系統(tǒng)LE-SVDD異常監(jiān)測方法。對海量數(shù)據(jù)進(jìn)行降維，用獲得的特征樣本來建立監(jiān)測模型，從而判斷系統(tǒng)的故障模式。

1 拉普拉斯特征映射

拉普拉斯特征映射(LE)是一種流行學(xué)習(xí)方法[11]，是局部線性嵌入(locally-linear embedding,簡稱LLE)方法的一個變種，其基本思想是在高維特征空間中距離很近的點(diǎn)投影到低維空間后距離也應(yīng)該很近，使用一個有權(quán)無向圖來描述一個流形，通過圖嵌入的方式找到高維數(shù)據(jù)的低維嵌入。流形屬于拓?fù)鋵W(xué)上的一個概念，表示一個局部處于歐幾里得的空間，該空間上任意一點(diǎn)都存在一個鄰域，在該鄰域內(nèi)，拓?fù)浣Y(jié)構(gòu)與空間中的單位圓相同。假設(shè)高維空間Rd中的樣本數(shù)據(jù)集X={x1,x2,…,xn}，xi∈Rd(i=1,2,…,n)，xj∈Rd(j=1,2,…,n)，且xi≠xj，高維樣本數(shù)據(jù)點(diǎn)xi和xj在原始空間中是距離較近的兩個樣本點(diǎn)，即xj是xi的k個近鄰點(diǎn)之一，點(diǎn)xi和xj之間的歐式距離定義為d(i,j)。LE方法基于圖譜理論，使用一個正的權(quán)值Wij來聯(lián)系點(diǎn)xi和點(diǎn)xj，通常使用熱核函數(shù)來設(shè)置權(quán)。熱核函數(shù)定義如下

(1)

其中：σ2為比例參數(shù)。

LE構(gòu)造的低維空間嵌入目標(biāo)函數(shù)為

(2)

在滿足流形結(jié)構(gòu)對域的約束yTDy=1和單點(diǎn)約束yTDy=0基礎(chǔ)上，最小化目標(biāo)函數(shù)，求解步驟相當(dāng)于求解式(3)的最小特征值問題

Ly=λDy

(3)

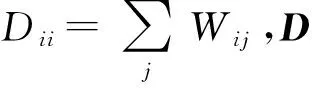
LE算法計算步驟總結(jié)如下。

1) 輸入樣本X={x1,x2,…,xn}，xi∈Rd(i=1,2,…,n)，近鄰點(diǎn)數(shù)為k，計算每個點(diǎn)xi的k個最近鄰點(diǎn)，1≤i≤N。

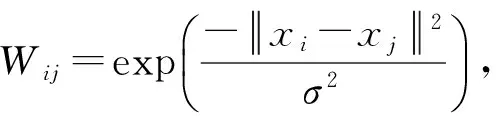
3) 求解目標(biāo)函數(shù)的最小誤差，相當(dāng)于求解拉普拉斯算子的廣義特征向量問題：求得式(3)最小r個非零特征值對應(yīng)的特征向量{φ1,φ2,…,φr}，嵌入結(jié)果表示為T=[φ1,φ2,…,φr]T。

從拉普拉斯特征映射的算法推導(dǎo)可知，拉普拉斯特征映射只需要很少的計算量，因此算法速度在流形學(xué)習(xí)的若干算法中最快。Belkin和Niyogi在理論上證明了LE算法的收斂性。流形學(xué)習(xí)的目標(biāo)是尋找數(shù)據(jù)集中的內(nèi)在關(guān)系，發(fā)現(xiàn)高維數(shù)據(jù)集存在的低維流形特征，將觀測數(shù)據(jù)在低維嵌入空間中進(jìn)行展開，在保證數(shù)據(jù)流形結(jié)構(gòu)不變的前提下實現(xiàn)數(shù)據(jù)降維。在目前常用的流形學(xué)習(xí)算法中，僅需要指定幾個變量即可實現(xiàn)數(shù)據(jù)的非線性降維，同時參數(shù)對于降維效果的影響較小，這樣就避免了核方法參數(shù)選取困難的問題。

2 SVDD算法

SVDD是Tax[12]基于支持向量機(jī)(support vector machine,簡稱SVM)提出的一種單類數(shù)據(jù)分類算法。其思想是將目標(biāo)樣本作為整體，在特征空間尋找一個超球面對目標(biāo)樣本全部或盡可能多的包裹，以結(jié)構(gòu)風(fēng)險為目標(biāo)對超球面大小進(jìn)行優(yōu)化，并對未知數(shù)據(jù)進(jìn)行分類。

假設(shè)Rd空間存在樣本集X={x1,x2,…,xn}，n為樣本數(shù)目，存在這樣一個非線性的映射函數(shù)φ，可以將樣本x映射為高維特征空間F中的Φ(x)，即

φ:x→Φ(x) (x∈Rd,Φ(x)∈F)

(4)

目標(biāo)是最小化結(jié)構(gòu)風(fēng)險，即在特征空間F中尋找一個最小的超球面，使得該超球面能夠盡可能地包裹{Φ(xi)}(i=1～n)中的特征樣本點(diǎn)。圖1為SVDD算法示意圖。

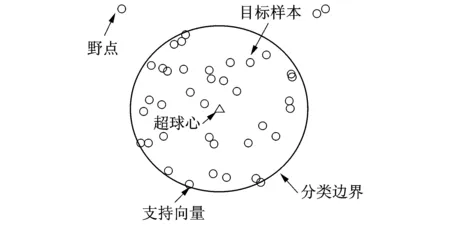
圖1 SVDD算法示意Fig.1 SVDD Algorithm diagram

SVDD算法與SVM類似，可以定義誤差函數(shù)最小化

F(R,a)=R2

(5)

約束為

‖xi-a‖2≤R2, ?i

(6)

為了允許異常值在訓(xùn)練集總存在，從xj到a的中心距離與R2不應(yīng)該完全一樣。大一點(diǎn)的距離應(yīng)該不利計算和辨識。因此這里引入松弛變量ζi≥0，最小化問題改為

(7)

其中：C為控制錯分的懲罰參數(shù)。

球體之內(nèi)所有對象的約束條件為

‖xi-a‖2≤R2+ζi(ζi≥0，?i)

(8)

其中：a為超球心坐標(biāo)；R為超球心到邊界距離；ζi≥0為松弛變量。

約束條件(8)使用拉格朗日泛函(Lagrange multiplier)并入式(7)得到

(9)

其中：ai≥0；λi≥0。

考慮到R,a,ζi時，L應(yīng)該是最小化；考慮到αi,γi時，L應(yīng)該是最大化。

SVDD中通常選取高斯核。在計算時，處于超球面上的樣本點(diǎn)滿足條件0≤ai≤C，這些點(diǎn)就是支持向量(support vector,簡稱SV)，超球球心a與半徑R由這些SV確定。

對于一個測試樣本點(diǎn)xtest，首先計算該點(diǎn)與超球心的距離

(10)

如果D≤R2，則接受測試點(diǎn)為目標(biāo)點(diǎn)，否則拒絕為目標(biāo)點(diǎn)。

3 基于特征樣本的LE-SVDD監(jiān)測方法

針對實際系統(tǒng)中存在的信號含噪和高維兩種問題，對降噪后的數(shù)據(jù)采用流行學(xué)習(xí)LE方法進(jìn)行降維，提取特征樣本，以特征樣本代替原始數(shù)據(jù)進(jìn)行建模，降低SVDD算法的復(fù)雜度。通過LE和SVDD組合應(yīng)用，并基于特征樣本的監(jiān)測方法應(yīng)用于本研究中。

3.1 SVDD訓(xùn)練樣本降維的必要性

實際工業(yè)系統(tǒng)監(jiān)測點(diǎn)位眾多，為了保證計量數(shù)據(jù)的正確性，同一監(jiān)測點(diǎn)位可能安裝若干計量設(shè)備，因此采集到的歷史數(shù)據(jù)集中就產(chǎn)生了大量的冗余信息。當(dāng)以這樣一種數(shù)據(jù)集進(jìn)行建模時，訓(xùn)練樣本的采樣總數(shù)可能數(shù)以萬計，且單一訓(xùn)練樣本又具有較高維度，這時冗余信息及對特征影響小的分量信息就會對建模產(chǎn)生較大影響，從而影響識別效果。

對訓(xùn)練樣本降維存在若干好處，其中最重要的一點(diǎn)是會使算法建模復(fù)雜度減少并提升識別效果。這是因為約簡訓(xùn)練樣本維度不僅會消除冗余信息造成的影響，同時會解決海量數(shù)據(jù)帶來的維數(shù)災(zāi)難問題。另外，維度約簡過程可獲取設(shè)備狀態(tài)的主要影響因素，使得模型能夠更好地被理解。

分析現(xiàn)有的數(shù)據(jù)挖掘模型，用于數(shù)據(jù)維數(shù)約簡的方法可歸納為兩種：特征選擇及特征提取。特征選擇能剔除不相關(guān)或冗余的特征，從而達(dá)到減少特征個數(shù)、提高模型精確度的目的。其計算過程是在全部特征集中產(chǎn)生一個特征子集，然后用評價函數(shù)對特征子集進(jìn)行評價，采用模擬退火、遺傳算法等算法對過程進(jìn)行優(yōu)化，直到挑選出符合評價指標(biāo)的結(jié)果。但是該方法計算時間較長，且提取的特征并非是一成不變的，因此不適應(yīng)于在線監(jiān)測。流形學(xué)習(xí)等數(shù)據(jù)特征提取方法是對原始數(shù)據(jù)進(jìn)行空間投影，把n維原始數(shù)據(jù)映射為m維特征數(shù)據(jù)，計算時間短，能夠處理非線性數(shù)據(jù)，因此在SVDD建模過程前的訓(xùn)練樣本維數(shù)約簡采用特征提取方法處理。

SVDD方法的訓(xùn)練過程實際上就是求解凸二次規(guī)劃問題，凸二次規(guī)劃問題的計算復(fù)雜度為O(n3)，因此降低訓(xùn)練樣本維度將會大大減少模型訓(xùn)練時間，降低了算法對計算機(jī)內(nèi)存和運(yùn)算時間的要求。

3.2 特征樣本LE-SVDD建模步驟

特征樣本建模的LE-SVDD異常監(jiān)測方法與原始SVDD異常狀態(tài)監(jiān)測方法的不同之處在于：新方法使用了流形降維后的特征樣本建立監(jiān)測模型；而傳統(tǒng)SVDD方法直接使用原始數(shù)據(jù)。

離線訓(xùn)練時，首先，對訓(xùn)練樣本進(jìn)行小波包分解重構(gòu)，消除高斯噪聲影響，對消噪后的數(shù)據(jù)進(jìn)行指數(shù)加權(quán)移動平均；然后，對處理得到的數(shù)據(jù)歸一化，消除量綱影響，記錄訓(xùn)練樣本的均值和方差，對歸一化后的數(shù)據(jù)進(jìn)行非線性降維，減少SVDD算法的計算復(fù)雜度，節(jié)省計算和存儲資源；最后，使用降維得到的特征樣本進(jìn)行LE-SVDD建模，對異常樣本進(jìn)行監(jiān)測。

在線監(jiān)測時，采集新的數(shù)據(jù)樣本，進(jìn)行歸一化，利用LE算法的線性近似映射矩陣求得降維后的低維樣本點(diǎn)，計算低維樣本點(diǎn)與SVDD超球中心的距離。若處在SVDD超球面外，則可判定為系統(tǒng)狀態(tài)發(fā)生異常，后續(xù)轉(zhuǎn)入系統(tǒng)異常狀態(tài)識別階段；否則認(rèn)為系統(tǒng)處于正常工況條件，繼續(xù)對系統(tǒng)狀態(tài)進(jìn)行監(jiān)測。基于特征樣本SVDD的系統(tǒng)狀態(tài)在線監(jiān)測流程如圖2所示，可分為離線建模及在線監(jiān)測兩部分。

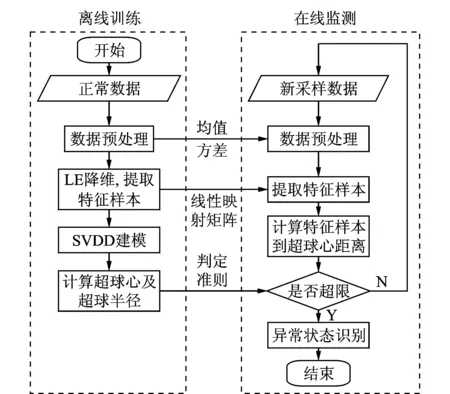
圖2 特征樣本LE-SVDD狀態(tài)監(jiān)測流程圖Fig.2 Characteristic sample LE-SVDD condition monitoring flow chart

算法步驟如下：

1) 獲取訓(xùn)練樣本X={x1,x2,…,xn}，xi∈Rd，小波包分解去噪，進(jìn)行指數(shù)加權(quán)移動平均，歸一化消除量綱影響；

2) 使用LE對處理后的數(shù)據(jù)進(jìn)行非線性降維，獲取特征樣本集，計算線性近似映射矩陣T；

3) 在特征樣本集上進(jìn)行SVDD建模；

4) 對于新進(jìn)數(shù)據(jù)進(jìn)行歸一化處理，投影后得到特征空間樣本Y=Tx，監(jiān)測是否超出判定值。

3.3 狀態(tài)監(jiān)測結(jié)果評價標(biāo)準(zhǔn)與指標(biāo)

為了保證復(fù)雜機(jī)電系統(tǒng)狀態(tài)監(jiān)測效果的準(zhǔn)確性和有效性，首先要確定評價標(biāo)準(zhǔn)。筆者通過對比選用最優(yōu)的參數(shù)作為標(biāo)準(zhǔn)，參考的數(shù)據(jù)信號包括溫度、壓力、振動和流量等。

流程工業(yè)復(fù)雜系統(tǒng)狀態(tài)監(jiān)測模型的建立依賴于預(yù)先提取的系統(tǒng)正常工況下的離線歷史數(shù)據(jù)。為了給出一種可信的綜合性故障或異常監(jiān)測評價指標(biāo)，兼顧統(tǒng)計學(xué)中的兩種錯誤類型，使用異常狀態(tài)下的漏報率(missed detection rate，簡稱MDR)及正常工況下的誤報率(false alarm rate，簡稱FAR)作為衡量監(jiān)測結(jié)果可信度的指標(biāo)。

MDR和FAR的數(shù)學(xué)表達(dá)式為

(11)

其中：NN,F為測試樣本集中正常狀態(tài)數(shù)據(jù)被判定為異常點(diǎn)的個數(shù)；NM為測試樣本集中異常狀態(tài)數(shù)據(jù)被判定為正常點(diǎn)的個數(shù)；NN為測試樣本集中正常樣本總數(shù)；NF為測試樣本集中異常樣本總數(shù)。

4 仿真實驗

4.1 TE過程故障模式

TE過程是以Eastman化學(xué)公司的一個實際生產(chǎn)流程為基礎(chǔ)提出的一個標(biāo)準(zhǔn)測試過程[13]，它是一個分布式復(fù)雜機(jī)電系統(tǒng)的典范，包括5個主要操作單元：反應(yīng)器、冷凝器、汽液分離器、循環(huán)壓縮機(jī)和汽提塔(解吸塔)。

TE過程一共預(yù)設(shè)了21種故障模式。這些故障模式內(nèi)故障(identity value，簡稱IDV)中的IDV(3)，IDV(9)，IDV(15)對于數(shù)據(jù)變化影響較小，多元統(tǒng)計方法對于這幾種故障的檢出率很低，本研究就不再將這幾種故障模式作為仿真對象。TE過程故障如表1所示。

表1 TE過程故障

4.2 異常監(jiān)測效果對比

本研究仿真中選取了故障5，10，16和20共計4種故障模式作為研究對象，進(jìn)行若干組實驗，對比組合方法和單一方法在異常狀態(tài)識別效果上的差別。由于訓(xùn)練樣本進(jìn)行歸一化并消除量綱影響，因此以下分析圖中均無量綱。

1) 圖形對比。首先，使用傳統(tǒng)SVDD方法進(jìn)行異常狀態(tài)監(jiān)測。核函數(shù)采用高斯核函數(shù)，核參數(shù)取值為18，各故障模式的異常檢出效果如圖3所示。從圖中可以看出，傳統(tǒng)SVDD方法對于第5類故障能夠在故障出現(xiàn)的第一時刻監(jiān)測到異常狀態(tài)的發(fā)生，但是過了一段時間之后，又無法監(jiān)測到異常；而對于故障10，16，20的識別效果很不理想。

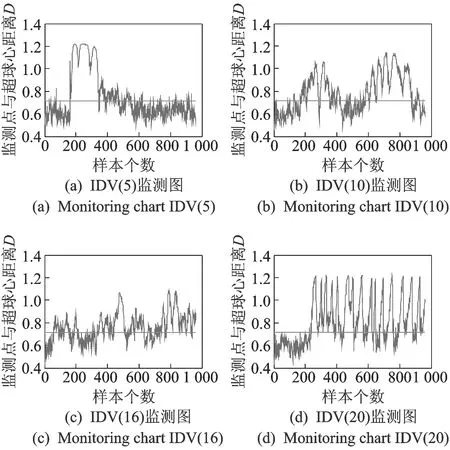
圖3 基于SVDD的故障監(jiān)測效果圖Fig.3 SVDD-based fault monitoring effect picture

出現(xiàn)上述結(jié)果是因為故障5由冷凝器冷卻水入口溫度發(fā)生階躍性變化引起的。故障5是一類對過程影響較小的故障模式。控制系統(tǒng)通過調(diào)節(jié)冷卻水的流量變化對系統(tǒng)進(jìn)行補(bǔ)償控制。大約在第360個采樣點(diǎn)開始，補(bǔ)償起到調(diào)節(jié)作用，將變量值恢復(fù)到正常值，但是故障確實是存在的，因此故障5的異常監(jiān)測失效。其他幾類故障模式的監(jiān)測雖未失效，但漏報率和誤報率均較高。綜上所述，單獨(dú)使用SVDD方法對TE過程進(jìn)行異常監(jiān)測未取得良好效果。

為了得到更準(zhǔn)確的異常狀態(tài)識別結(jié)果，按照以上提到的特征樣本LE-SVDD監(jiān)測方法步驟，重新對上述所選故障模式進(jìn)行狀態(tài)預(yù)測。這里SVDD仍然選取與之前相同的核函數(shù)形式及核參數(shù)大小，數(shù)據(jù)處理及消噪方法也完全相同。

實際工業(yè)過程監(jiān)測變量因存在關(guān)聯(lián)性，使得當(dāng)前時刻的系統(tǒng)狀態(tài)會收到歷史數(shù)據(jù)影響，因此，在系統(tǒng)出現(xiàn)異常或故障時，異常狀態(tài)會隨著時間進(jìn)行推移。指數(shù)權(quán)重移動平均(exponentially weighted moving average，簡稱EWMA)是一種常見的處理工業(yè)系統(tǒng)動態(tài)行為的方法。對數(shù)據(jù)進(jìn)行EWMA處理，可以提高監(jiān)測結(jié)果的準(zhǔn)確性及可靠性，減少誤報和漏報。EWMA若選擇較大的權(quán)重，可對當(dāng)前狀態(tài)進(jìn)行及時反應(yīng)；若選擇小的權(quán)重，可監(jiān)測系統(tǒng)變化趨勢。本研究中權(quán)重系數(shù)選為0.5。

采用本方法對選定故障類型進(jìn)行監(jiān)測，統(tǒng)計量預(yù)先進(jìn)行EWMA處理，監(jiān)測效果如圖4所示。

2) 參數(shù)對比。為了更清晰的比較兩種降維方法對于監(jiān)測結(jié)果的影響，計算出了兩種故障模式下分別采用局部保持投影(locally preserving projection，簡稱LPP)和LE降維后SVDD監(jiān)測方法的漏報率和誤報率，結(jié)果如表2所示。從圖表中可以看出，對于具有很強(qiáng)非線性的故障5和故障16，LE降維方法的優(yōu)勢體現(xiàn)在其非線性特征提取之上，LPP算法在非線性數(shù)據(jù)的處理方面則略有不足。

雖然LE的漏報率偏高，但是誤報率遠(yuǎn)遠(yuǎn)小于LPP方法。因此，本研究選擇LE方法進(jìn)行非線性降維，提取數(shù)據(jù)特征。選定的故障類型漏報率及誤報率見表3。

圖4 提出方法的監(jiān)測效果圖Fig.4 Proposed method’s monitoring effect picture

Tab.2 Comparisons of monitoring results of LPP and LE dimensionality reduction methods

故障模式LPP(r=18,k=12)LE(r=18,k=12)漏報率/%誤報率/%漏報率%誤報率%故障5010.62500.625故障162.540.00013.8752.500

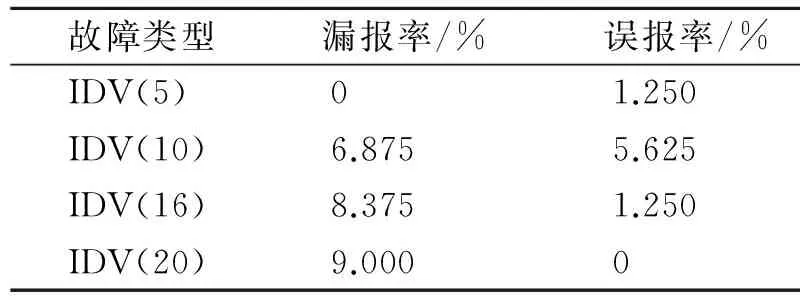
表3 特征樣本LE-SVDD監(jiān)測結(jié)果

根據(jù)經(jīng)驗，在復(fù)雜機(jī)電系統(tǒng)故障監(jiān)測過程中，如果大部分情況下漏報率和誤報率低于10%，則可以得出準(zhǔn)確的結(jié)果。分析結(jié)果可知，對于TE過程幾種類型的故障模式，筆者提出的方法的漏報率和誤報率均較低，說明該方法具有很好的應(yīng)用效果。

為了說明所采用方法的適用性，筆者對比了其他異常檢測方法在TE過程數(shù)據(jù)中的結(jié)果。文獻(xiàn)[14]提到了兩種異常數(shù)據(jù)監(jiān)測分析方法，即多維主成分分析-支持向量數(shù)據(jù)描述(multidimensional PCA-SVDD,簡稱MDPCA-SVDD)和局部切空間算法-特征樣本的支持向量數(shù)據(jù)描述(local tangent space alignment-feature samples SVDD,簡稱LTSA-FSSVDD)的混合模型。將本研究方法的監(jiān)測結(jié)果與以上兩種方法結(jié)果進(jìn)行對比，以漏報率作為評價標(biāo)準(zhǔn)，得到了對比結(jié)果如表4所示，其中：Ω為統(tǒng)計量。

表4 TE過程故障監(jiān)測結(jié)果(漏報率)的對比

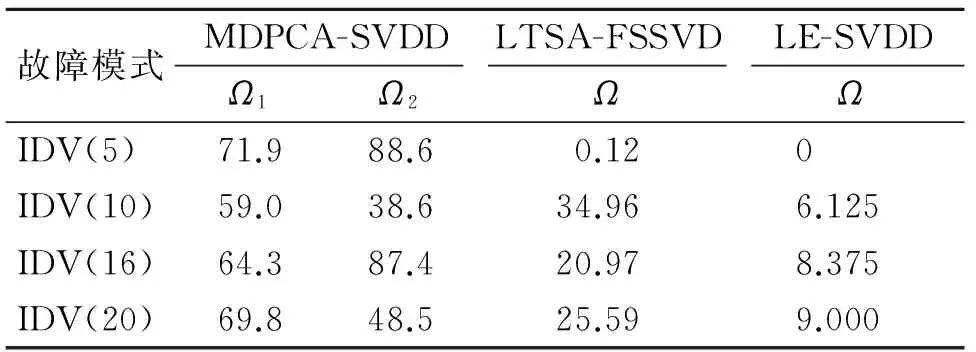
Tab.4 Comparison of fault monitoring results in TE process (false negative rate) %

文獻(xiàn)[15]提出了一種基于集成熵的核主成分分析(integrated entropy kernel principal component analysis,簡稱IEKPCA)故障監(jiān)測方法，以誤報率和漏報率作為評價指標(biāo)進(jìn)行對比，得到對比結(jié)果如表5所示。雖然故障IDV(11)的LE-SVDD方法的誤報率比IEKPCA方法偏高，但是比重小，不能影響總體的比率。

表5 IEKPCA與LE-SVDD對比結(jié)果

以上對比得到的結(jié)果均顯示了本研究方法在復(fù)雜機(jī)電系統(tǒng)異常監(jiān)測上的有限性和優(yōu)越性，即單獨(dú)使用SVDD方法具有一定的局限性，漏報率升高，效果不佳。LE方法具有很好的降維能力，降維后通過SVDD進(jìn)行監(jiān)測能夠得到很好的故障識別效果，并能夠顯示出識別的優(yōu)越性。這說明降維和異常點(diǎn)監(jiān)測方法的組合技術(shù)是合理的，能夠大大提高故障監(jiān)測的準(zhǔn)確性。

5 結(jié)束語

提出了一種基于特征樣本的復(fù)雜機(jī)電系統(tǒng)LE-SVDD狀態(tài)監(jiān)測方法。通過在TE仿真過程中進(jìn)行實驗，結(jié)果表明該方法在狀態(tài)監(jiān)測中具有良好的非線性和高維數(shù)據(jù)處理能力。同其他方法對比表明，該方法具有一定的優(yōu)越性。筆者以異常狀態(tài)監(jiān)測和故障模式識別方法為基礎(chǔ)，研究了系統(tǒng)異常狀態(tài)監(jiān)測診斷集成模型構(gòu)建方法。以調(diào)研企業(yè)壓縮機(jī)組系統(tǒng)為研究對象，以生產(chǎn)設(shè)備長期運(yùn)行的集散控制系統(tǒng)的監(jiān)測數(shù)據(jù)為基礎(chǔ)，根據(jù)企業(yè)記錄的事故案例建立異常案例庫，采用LE-SVDD集成方法研究復(fù)雜機(jī)電系統(tǒng)異常狀態(tài)監(jiān)測問題，結(jié)果表明組合式異常狀態(tài)識別方法可以有效監(jiān)測到系統(tǒng)運(yùn)行過程中異常事件的發(fā)生。

[1] Frank P M. Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy: a survey and some new results[J]. Automatica, 1990, 26(3): 459-474.

[2] Bansal S, Sahoo S, Tiwari R, et al. Multiclass fault diagnosis in gears using support vector machine algorithms based on frequency domain data[J]. Measurement, 2013, 46(9): 3469-3481.

[3] Naimul M K, Riadh K, Imran S A, et al. Covariance-guided one-class support vector machine[J]. Pattern Recognition, 2014, 47(6): 2165-2177.

[4] Diego F F, David M R, Oscar F R, et al. Automatic bearing fault diagnosis based on one-class v-SVM[J]. Computers & Industrial Engineering, 2013, 64(1): 357-365.

[5] Jiang Zhiqiang, Feng Xilan, Feng Xianzhang, et al. A study of SVDD-based algorithm to the fault diagnosis of mechanical equipment system[J]. Physics Procedia，2012, 33: 1068-1073.

[6] Li Guannan, Hua Yunpeng, Chen Huanxin, et al. An improved fault detection method for incipient centrifugal chiller faults using the PCA-R-SVDD algorithm[J]. Energy and Buildings, 2016, 116 (15): 104-113.

[7] Issam B K, Claus W, Mohamed L. Kernel k-means clustering based local support vector domain description fault detection of multimodal processes[J]. Expert Systems with Applications, 2012, 39(2): 2166-2171.

[8] 陳偉，賈慶軒，孫漢旭. 利用小波包和 SVDD的分揀機(jī)軸承故障診斷[J]. 振動、測試與診斷，2012，32(5)： 762-766.

Chen Wei，Jia Qingxuan，Sun Hanxu. Bearing fault detection for forting machine using wavelet packet and SVDD[J]. Journal of Vibration，Measurement & Diagnosis，2012，32(5)：762-766. (in Chinese)

[9] 孫文柱，曲建嶺，袁濤，等. 基于改進(jìn) SVDD 的飛參數(shù)據(jù)新異檢測方法[J]. 儀器儀表學(xué)報，2014，35(4)： 932-939.

Sun Wenzhu，Qu Jianling，Yuan Tao， et al. Flight data novelty detection method based on improved SVDD[J]. Chinese Journal of Scientific Instrument, 2014，35(4)：932-939. (in Chinese)

[10]Zhao Yang, Wang Shengwei, Xiao Fu. Pattern recognition-based chillers fault detection method using support vector data description (SVDD)[J]. Applied Energy, 2013, 112: 1041-1048.

[11]Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6): 1373-1396.

[12]Tax D M J, Duin R P W. Support vector data description[J]. Machine Learning, 2004, 54(1): 45-66.

[13]Downs J J, Vogel E F. A plant-wide industrial-process control problem[J]. Comuters & Chemical Engineering, 1993,17(3): 245-255.

[14]張少捷，王振雷，錢鋒. 基于 LTSA 的 FS-SVDD 方法及其在化工過程監(jiān)控中的應(yīng)用[J]. 化工學(xué)報，2010, 61(8)：1894-1900.

Zhang Shaojie，Wang Zhenlei，Qian Feng. FS-SVDD based on LTSA and its application to chemical process monitoring[J]. CIESC Journal，2010，61(8)：1894-1900. (in Chinese)

[15]梁銀林. 基于集成熵KPCA-SSVM的復(fù)雜機(jī)電系統(tǒng)狀態(tài)監(jiān)測診斷方法研究[D]. 西安：西安交通大學(xué)，2014.

10.16450/j.cnki.issn.1004-6801.2017.03.008

國家自然科學(xué)基金資助項目(51375375)；機(jī)械制造系統(tǒng)工程國家重點(diǎn)實驗室(西安交通大學(xué))開放課題資助項目(sklms2015009)

2016-05-30；

2017-02-20

TH17； TH165+.3

亞森江·加入拉，男，1972年9月生，在職博士生。主要研究方向為復(fù)雜機(jī)電系統(tǒng)狀態(tài)監(jiān)測與診斷。曾發(fā)表《基于時間序列分析的復(fù)雜機(jī)電系統(tǒng)狀態(tài)數(shù)據(jù)的檢驗方法》(《新疆大學(xué)學(xué)報：自然科學(xué)維吾爾文版》2014年第35卷第1期)等論文。 E-mail:yasenjiang@stu.xjtu.edu.cn