求解矩陣方程的一種迭代法

張 騫, 周 蕾, 袁永新

(湖北師范學院數學與統計學院, 湖北 黃石 435002)

求解矩陣方程的一種迭代法

張 騫, 周 蕾, 袁永新

(湖北師范學院數學與統計學院, 湖北 黃石 435002)

考慮一類矩陣方程AXB+CYD+E的解, 其中X是未知的對稱矩陣,Y是未知的反對稱矩陣. 當矩陣方程是相容時, 建立了共軛梯度法去求解矩陣方程, 并且證明通過有限次的迭代可以得到矩陣方程的解. 同時通過選擇一些特殊的初始矩陣, 可以得到它的最小范數解.

矩陣方程; 共軛梯度法; 對稱解; 反對稱解

0 引言

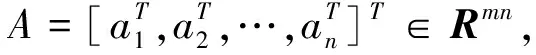
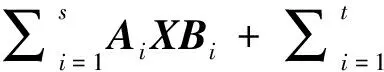
設矩陣A,C∈Rm×n,B,D∈Rn×p,E∈Rm×p是已知的, 找到矩陣X∈SRn×n,Y∈SSRn×n滿足下面矩陣方程

(1)

1 主要結果

下面我們將給出求解方程(1)的一種迭代算法.

算法Ⅰ.

1) 輸入矩陣A,B,C,D,E和任意的初始矩陣X1∈SRn×n,Y1∈SSRn×n.

2)R1=E-AX1B-CY1DPX,1=ATR1BT,PY,1=CTR1DT

3) 如果Rk=0或者Rk≠0,QX,k=0,QY,k=0停止; 否則進行(4).

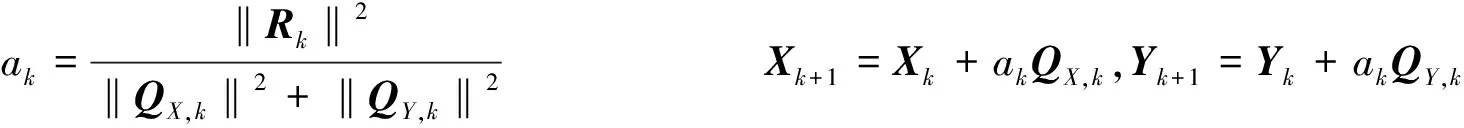
顯然, 對所有的Xk,QX,k∈SRn×n,Yk,QY,k∈SSRn×n.

引理1 由算法Ⅰ產生的{Ri}, 有

(2)

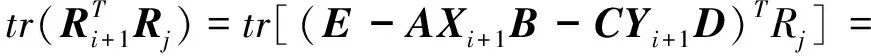
tr[(E-A(Xi+aiQX,i)B-C(Yi+aiQY,i)D)TRj]=

引理2 由算法Ⅰ產生的{Ri},{QX,i},{QY,i}有

(3)

證明 我們用數學歸納法證明引理2.

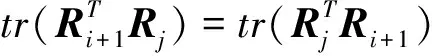
對i=j=1,由式(2)可得

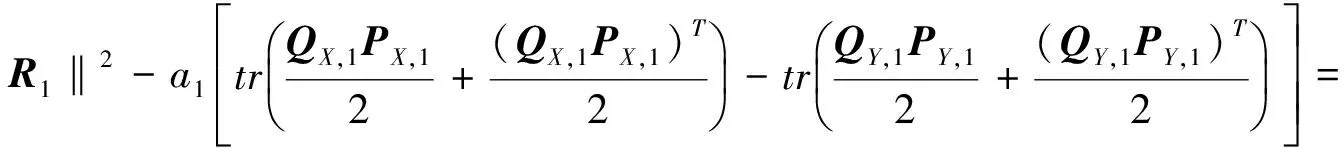
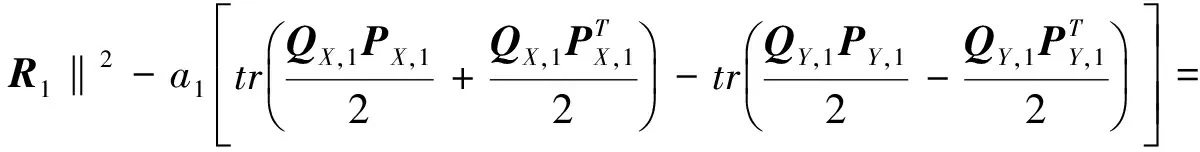
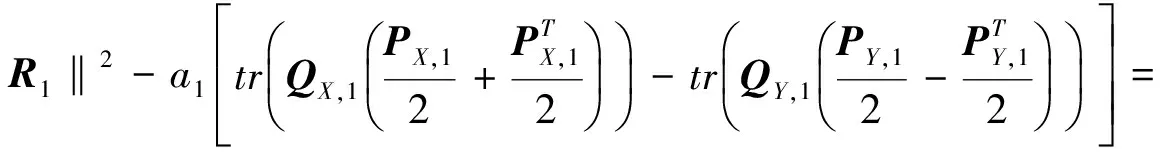
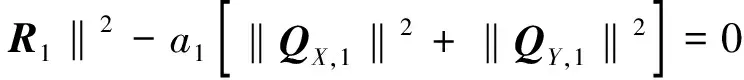
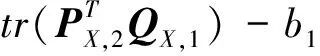
假設對i=s-1時, 關系式(3)成立, 下面證明i=s時結論也成立.

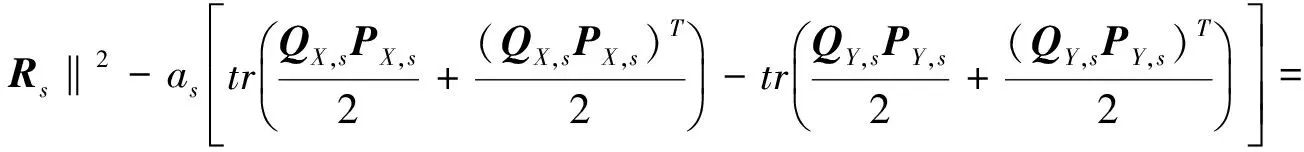
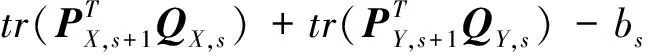
所以, 對任意i=s, 關系式(3)都是成立的.

-as[tr(QX,sPX,j)-tr(QY,sPY,j)]=

所以

由數學歸納法可知, 引理2得到了證明.

引理3 設(X*,Y*)是方程(1)的任意一個解, {Xk},{Yk}是由算法Ⅰ得到的, 則

(4)

證明 我們用數學歸納法來證明這個引理.

當k=1時,

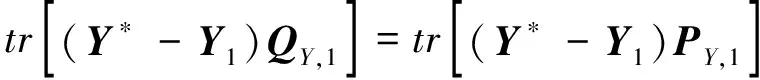
所以

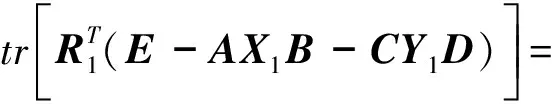
當k=s時, 式(4)成立, 下面我們證明k=s+1也成立.

因為

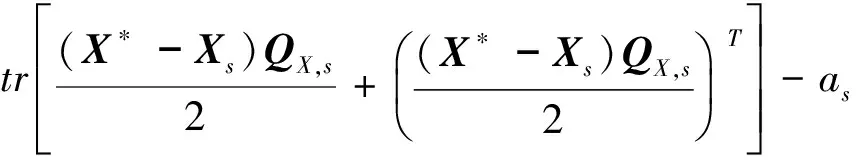
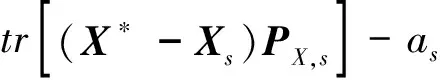
同理可得

所以

可得

由數學歸納法可知, 引理3得到了證明.

定理1 假設方程(1)是相容的, 那么對于任意的初始矩陣X1∈SRn×n,Y1∈SSRn×n. 在誤差范圍內,方程(1)的解可以通過算法Ⅰ進行有限次迭代得到.

引理4[13]設x是方程Ax=b的一個解, 如果x∈R(AT), 則x是方程Ax=b唯一的最小范數解.

由引理4和方程(1), 可得

假設S,H是任意的矩陣, 我們可得

我們選擇X1=ATHBT+BHTA,Y1=CTSDT-DSTC,則由算法Ⅰ產生的{Xi},{Yi}滿足

由引理4和上面的討論, 我們可以得到下面的結果.

定理2 假設方程(1)是相容的, 如果我們選擇初始矩陣

X1=ATHBT+BHTA,Y1=CTSDT-DSTC

其中S,H是任意的矩陣, 特別S=H=0, 則由算法Ⅰ, 通過有限步迭代可以得到方程(1)唯一的最小范數解.

2 數值例子

例. 設

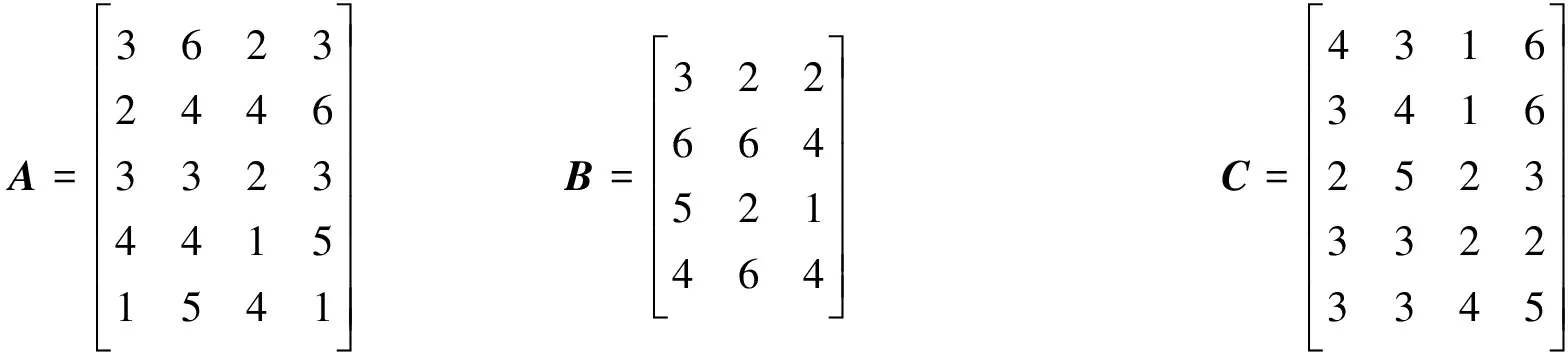
1) 求矩陣方程AXB+CYD=E最小范數解, 其中X1∈SR4×4,Y1∈SSR4×4.

令初始矩陣X=Y=0,由于計算過程中會產生誤差, 我們令誤差‖Rk‖≤10-10.時, 迭代停止. 由算法Ⅰ, 迭代51次后可得到

此時誤差‖R51‖=3.4864e-011. 所以在誤差范圍內, 通過算法Ⅰ得到了問題(1)的解.

[1]Chen W, Wang X, Zhong T. The structure of weighting coefficient matrices of Harmonic differential quadrature and its application, Commun[J]. Numer Methods Eng. 1996, 12: 455～460.

[2]Datta L, Morgera S. Some results on matrix symmetries and a pattern recognition application[J]. IEEE Trans. Signal Process, 1986, 34:992～994.

[3]Weaver J. Centrosymmetric (cross-symmetric) matrices, their basic properties, eigenvalues, and eigenvectors[J]. Amer. Math. Monthly, 1985, 92: 711～717.

[4]Datta L, Morgera S. On the reducibility of centrosymmetric matrices-applications in engineering problems[J]. Circuits Systems Signal Process, 1989, 8:71～96.

[5]Delmas J. On adaptive EVD asymptotic distribution of centro-symmetric covariance matrices[J]. IEEE Trans. Signal Process, 1999, 47:1402～1406.

[6]Baksalary J K, Kala R. The matrix equationAXB+CYD=E[J]. Linear Algebra Appl, 1980, 30: 141～147.

[7]Wang Q W, Zhang H S, Yu S W. On solutions to the Quaternion matrix equationAXB+CYD=E[J]. Electronic Journal of Linear Algebra, 2008, 17:343～358.

[8]Xu G P, Wei M S, Zheng D S. On the solution of matrix equationAXB+CYD=F[J]. Linear Algebra Appl, 1998, 279:93～109.

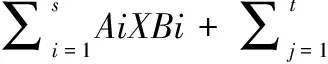
[10]彭振贊.幾類矩陣擴充問題和幾類矩陣方程問題[D]. 長沙: 湖南大學, 2003.

[11]Peng Y X, Hu X Y, Zhang L. An iteration method for the symmetric solutions and the optimal approximation solution of the matrix equation AXB=C[J]. Appl. Math. Comput, 2005, 160:763～777.

[12]Huang G X, Yin F, Guo K. An iterative method for the skew-symmetric solution and the optimal approximate solution of the matrix equation[J]. Computational and Applied Mathematics , 2008, 212:231～244.

[13]Ben-Israel A, Greville T N E. Generalized inverse: theory and applications[J]. Wiley, New York,1974.

An iterative method for solution of the matrix equationAXB+CYD=E

ZHANG Qian, ZHOU Lei, YUAN Yong-xin

(College of Mathematics and Statistics, Hubei Normal University, Huangshi 435002, China)

We consider the solution ofAXB+CYD=E, whereXis a unknown symmetric matrix,Yis a unknown skew-symmetric matrix. When the matrix equation is consistent, we propose a conjugate gradient method to solve the equation and prove that a solution (X*,Y*) can be obtained within finite iterative steps. Furthermore, we show that the minimum-norm solution of the equation can be obtained by choosing a special kind of initial matrices.

Matrix equation; conjugate gradient method; symmetric solution; skew-symmetric solution

2016—10—11

張騫(1989— )，男，河南省項城市人，碩士研究生，主要研究方向為代數學.

O246

A

2096-3149(2017)01- 0061-06

10.3969/j.issn.2096-3149.2017.01.013