十一種技巧破解導數所有難題

■陜西省洋縣中學 何記英

十一種技巧破解導數所有難題

■陜西省洋縣中學 何記英

導數的工具性和應用性一直是高考考查的熱點,主要題型有：利用導數研究函數的圖像和性質進而比較大小關系、求和、求證不等式、求解參數范圍、研究零點、求解探索性和新定義問題、研究變化率的實際問題以及簡化證明數列求和的不等式等。下面歸類分析導數應用的新穎試題。

一、利用導數研究函數的單調性及極值

(1)求a的值及f(x)的單調區間;

(2)?x∈[0,3],使f(x)＜b2,求b的取值范圍。

解析：(1)f'(x)=3a x2-3(a+2)x+6,

則f'(2)=0,故a=1。所以f'(x)=3x2-9x+6=3(x2-3x+2)=3(x-1)(x-2)。

令f'(x)＞0,則x＜1或x＞2;

令f'(x)＜0,則1＜x＜2。

所以f(x)的單調增區間為(-∞,1), (2,+∞),單調減區間為(1,2)。

(2)由(1)知f(x)的極小值為f(2)=b +2,f(x)的極大值為

所以f(x)min=b＜b2,解得b＜0或b＞1。故b的取值范圍為(-∞,0)∪(1,+∞)。

點評：求函數極值的方法步驟：①求出函數的定義域。②求出函數的導函數f'(x),解方程f'(x)=0,求出x的值。③判定在定義域內導函數為0的點兩側的單調性;并求出在該點的原函數值。④先增后減,為極大值點,先減后增為極小值點;兩側單調性相同,則該點不是極值點。

二、運用導數運算法則構造函數，研究單調性比較大小

例2 已知函數f(x)在R上可導,且?x∈R,均有f(x)＞f'(x),則有( )。

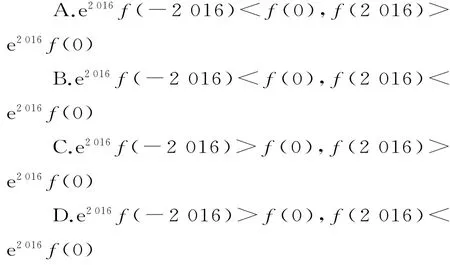
解析：從f(x)＞f'(x)這個條件,無法著手,此時我們要借助于選擇題中選項的提示功能。結合所學知識分析可知,要引入函數y=ex。由f(x)＞f'(x)?f(x)-f'(x)

點評：根據導數法則和題設條件,將題設條件合理變形,然后對照法則和導數公式構造新函數,如本題f(x)-f'(x)＞0,注意商的導數和y=ex的導數特征可構造h(x)=,研究其性質比較大小。

三、構建輔助函數用導數研究圖像求解不等式

例3 已知定義在R上的函數f(x),滿足f(x)+2f'(x)＞0恒成立,且f(2)=為自然對數的底數),求不等式exf(x)的解集。

點評：超越不等式求解,先化簡通過移項變形為h(x)＞0,進而構造函數h(x),研究其圖像與x軸的交點位置,即可求得不等式的解集,這也是導數的一個重要應用。

四、構建輔助函數研究函數的奇偶性和單調性，求參數范圍

例4 設函數f(x)在R上存在導函數f'(x),?x∈R,有f(-x)+f(x)=x2,在(0,+∞)上f'(x)＜x。若f(4-m)-f(m)≥8 -4m,則實數m的取值范圍是( )。

A.-2,2[]

B.2,+∞[)

C.0,+∞[)

D.-∞,-2 ( ]∪2,+∞[)

解析：由題設f(4-m)-f(m)≥8-4m和f'(x)＜x構造輔助函數g(x)=f(x)-,注意到f(-x)+f(x)=x2,g(-x)所以g(-x)+g(x)=0,即g(x)為奇函數,且g(0)=0。

g'(x)=f'(x)-x＜0在(0,+∞)上恒成立,則g(x)為奇函數且在(0,+∞)上為遞減函數,于是f(4-m)-f(m)≥8-4m可轉化為依據單調性有4-m≤m,所以m≥2,選B。

點評：由題設f(4-m)-f(m)≥8-4m和f'(x)＜x及f(-x)+f(x)=x2,可構造輔助函數,證明g(x)為奇函數且在(0,+∞)上單調遞減是求解的關鍵。

五、構造函數用導數證明不等式

例5 已知函數f(x)=(x-1)l nx+ xl n(1-x)。

(1)證明函數f(x)=(x-1)l nx+ xl n(1-x)在定義域內是單調減函數;

(2)設0＜a＜b＜1,求證bb-1(1-b)b＜aa-1(1-a)a

因為x∈(0,1),所以l n[x(1-x)]＜0,所以f'(x)=l n[x(1-x)]-則函數f(x)= (x-1)l nx+xl n(1-x)在(0,1)上是單調減函數。

(2)注意0＜a＜b＜1和不等式的意義,要證bb-1(1-b)b＜aa-1(1-a)a,取對數只需證(b-1)l nb+bl n(1-b)＜(a-1)l na+ al n(1-a)成立。

由(1)知函數f(x)=(x-1)l nx+ xl n(1-x)在(0,1)上是單調減函數。

因為0＜a＜b＜1,所以f(a)＞f(b),即原不等式成立。

點評：利用導數研究函數的單調性,再用單調性來證明不等式是函數、導數、不等式綜合問題中的一個難點,注意試題的特征,對不等式要合理變形,如本題取對數(b-1)l nb+ bl n(1-b)＜(a-1)l na+al n(1-a),用已證函數的單調性,從而證得不等式。

六、構建函數，用導數求解不等式恒成立問題

解析：將不等式m [g(x1)-g(x2)]＞x1f(x1)-x2f(x2)轉化為m g(x1)-x1f(x1)＞m g(x2)-x2f(x2)。觀察不等式左右結構的對稱性,可以構造輔助函數＞0。

當x＞0時,函數q(x)嚴格單調遞增,即有q'(x)=m x-l nx-1≥0恒成立。

于是h(x)max=h(1)=1,故有m≥1。

因為m∈Z,m≤1,所以m=1。

點評：把不等式m g(x1)-g(x2) [

]＞x1f(x1)-x2f(x2)變形為m g(x1)-x1f(x1)＞m g(x2)-x2f(x2),使得x1僅出現在不等式左邊,而x2僅出現在不等式右邊,呈現出不等式左右兩邊形式一樣的對稱關系式,便于轉化為函數模型去解決問題。

七、利用導數幾何意義構造相切條件，確定變量所在位置

例7 已知函數f(x)=x2的圖像在點(x0,)處的切線為l,若l也與函數y =l nx,x∈(0,1)的圖像相切,則x0所在的區間是( )。

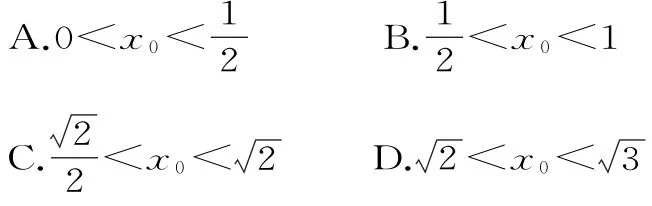
解析：由題意知f'(x)=2x,f(x0)= x20,所以l的方程為y=2x0(x-x0)+x20= 2x0x-x20。因為l也與函數y=l nx的圖像相切,令切點坐標為,所以l的方程為,所以因為x1∈(0,1),所以1+令g(x)=x2-l n 2x-1,x∈(1,+∞),則該函數的零點就是x0,排除A、B選項。又因為g'(x)=2x,所以g(x)在(1,+∞)上單調增。又g(1)=-l n 2＜0,g(2)=1-l n 22＜0,g(3)=2-l n23＞0,從而2＜x0＜。故應選D。

點評：兩曲線有公切線,借助導數的幾何意義構建兩切點之間的關系,再降元構建輔助函數,用導數研究其單調性,用零點存在性定理確定所求變量所在的區間,將導數的幾何意義和工具性以及構造函數與函數零點的判斷有機地交匯,探究過程耐人回味。

八、利用導數求解函數探索性問題

(1)當m=1時,求函數f(x)的單調性和極值。

(3)某同學發現：總存在正實數a、b(a＜b),使ab=ba。試問：他的判斷是否正確?若不正確,請說明理由;若正確,請求出a的取值范圍。(不需要解答過程)

解析：(1)易求函數定義域為(0,+∞),因為f(x)=x-l nx,,所以當0＜x＜1時,f'(x)＜0,此時f(x)單調遞減;當x＞1時,f'(x)＞0,此時f(x)單調遞增。

故f(x)只有極小值,且極小值為f(1)=1。

(2)由(1)知f(x)min=1。因為g'(x)=,所以當0＜x＜e時,g'(x)＞0, g(x)在(0,e]上單調遞增,所以g(x)max=

f(x)-g(x)≥f(x)min-故在(1)的條件下,

(3)正確,a的取值范圍是(1,e)。

理由如下,考慮數形結合。因為g(x)在 (0,e)上單調遞增,在(e,+∞)上單調遞減,且當x→0時,g(x)→—∞,當x→+∞時,g(x)→0,所以易知函數g(x)的大致圖像如圖1所示。

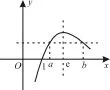
圖1

故總存在正實數a、b且1＜a＜e＜b,使得g(a)=g(b),即

點評：利用導數研究單調性可以證明不等式,再結合函數的性質作出其大致圖像,借助圖像就可以解決探索性問題,這是導數的又一個應用。

九、利用導數研究函數的新定義問題

(1)若函數f(x)與g(x)在公共定義域上具有相同的單調性,求實數m的值。

(2)若函數m(x),m1(x),m2(x)在公共定義域內滿足m1(x)＞m(x)＞m2(x)恒成立,則稱m(x)為從m1(x)至m2(x)的“過渡函數”。

(ⅰ)在(1)的條件下,探究從f(x)至g(x)是否存在無窮多個“過渡函數”,并說明理由。

(ⅱ)是否存在非零實數m,使得f(x)是從p(x)至g(x)的“過渡函數”?若存在,請求出非零實數m的取值范圍;若不存在,請說明理由。

解析：(1)易知f(x)與g(x)的公共定義域為(0,+∞),且在(0,1)上單調遞減,在(1,+∞)上單調遞增。又f'(x)則f'(1)=0,即m=-1。經檢驗,當m=-1時f(x)與g(x)在公共定義域上具有相同的單調性,故所求實數的值為-1。

令F(x)=f(x)-g(x)=x-l nx, x∈(0,+∞),則。故F(x)在(0,1)上單調遞減,在(1,+∞)上單調遞增,故F(x)min=F(1)=1,因此f(x)-g(x)≥1,即f(x)≥g(x)+1。

令h(x)=g(x)+t,t∈(0,1),則f(x)＞h(x)＞g(x)在(0,+∞)上恒成立。

故存在無窮多個從f(x)至g(x)的“過渡函數”。

(ⅱ)假設存在實數m,使得f(x)是從p(x)至g(x)的“過渡函數”,則在(0,+∞)上恒成立。令H(x)=f(x)-g(x)=ml nx+x,x∈(0, +∞),則

①當m＞0時,H'(x)＞0,故H(x)在(0,+∞)上單調遞增,且值域為R,此時f(x)-g(x)＞0不恒成立,故m＞0與假設不符。

②當m＜0時,令H'(x)=0,解得x= -m,可知H(x)在(0,-m)上單調遞減,在(-m,+∞)上單調遞增,故H(x)min= H(-m)=ml n(-m)-m,依題意知, ml n(-m)-m＞0,解得m＞-e,故-e＜m＜0;所以,當-e＜m＜0時,f(x)＞在g(x)上(0,+∞)恒成立。

綜上可知,不存在非零實數m,使得f(x)是從p(x)至g(x)的“過渡函數”。

點評：新定義的過渡函數,定義域相同且三個函數的大小關系滿足m1(x)＞m2(x)＞m3(x),實質是怎樣探究和應用這種不等關系。可以作差構建兩個輔助函數研究單調性尋求極值切入,構造這種不等關系,也可以由這種不等關系構建兩個輔助函數判斷是否有同時存在的條件。

十、利用“二次求導”求解綜合問題

當x＞1時,h'(x)＞0,則h(x)遞增,所以h(x)＞h(1)=-1。

因為h(3)=1-l n3＜0,h(4)=2-l n4＞0,故存在唯一x0,x0∈(3,4),使得h(x0) =0。

當1＜x＜x0時,h(x)＜0,x＞x0時, h(x)＞0,從而g'(x0)=0。

于是,當1＜x＜x0時,g'(x0)＜0,當x＞x0時,g'(x0)＞0。

g(x)在x=x0時取得最小值,即

由h(x0)=0得l nx0=x0-2,代入上式,得g(x)min=x0,即k＜g(x)min=x0。

由于k∈Z,x0∈(3,4),所以kmax=3。

點評：當f'(x)=0無法用初等方程求解時,可二次求導。二次求導與設而不求聯袂,化解一次求導函數零點“求之不得”的問題,用零點存在定理估算以及零點適合方程l nx0=x0-2的應用,都是求解超越函數不等式的常用方法。

十一、利用定積分求解數列和的不等式

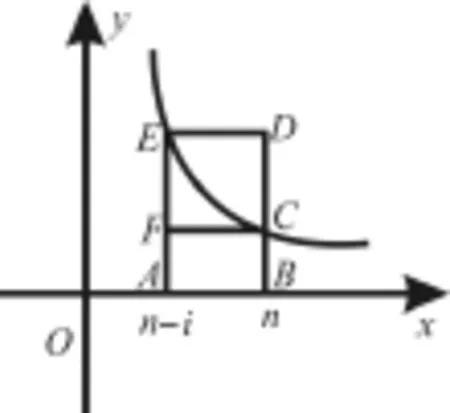
圖2

SABCF,從而=l nn-l n(n-i)。

相加后可以得到：

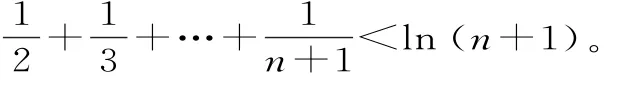
點評：挖掘待證不等式為數列和的不等式左右兩邊的幾何意義,通過構造函數利用定積分的幾何意義來解決問題,解法雖然綜合性強,但由于數形結合解法直觀便于操作。積分法證明不等式是一個新方法、新亮點,很值得品味。

(責任編輯 徐利杰)