基于數學名題的思維課堂實踐研究

◎蔣巧君

基于數學名題的思維課堂實踐研究

◎蔣巧君

“知識是手段，不是目的。思維才是最有效的。”但思維的隱形性增加了思維培養的難度。數學課堂上很多學生學習“抄近路”，回答問題只說答案。教師追問思考過程，學生表述不清，缺乏表達思考過程的能力。正因為抽象的思維隱形于學生的學習活動中，教師不能準確地把握學生的思維動態。更何況學生思維品質的提升，不是一朝一夕的事，是一個長期積累的過程。一節課的效果不能立竿見影，所以思維品質的培養容易被教師們忽視。如何建構思維課堂，提升學生思維品質呢？

一、為學生提供有思考價值的素材

數學名題是數學發展史中有一定的歷史故事與情節，有數學著作記載或民間流傳的有代表性的數學問題。如雞兔同籠、李白喝酒、以碗知僧、百錢白雞、韓信點兵……數學題之所以能成為名題 ,大多數是因富含哲理且寓于生活之中 ,讀之妙趣橫生而又回味無窮，因此很多名題都是大家所喜聞樂見的。教師要以數學名題為載體，適當介紹有關的背景知識，幫助學生感悟深厚的數學文化，體會數學在人類發展史中的作用。思維課堂要實現的條件是教師要掌握核心技術：教師自身提問的技術和激發學生提問的技術。一名優秀的教師，應該是學生思維的激發者，要讓學生有適當的時間和空間自主發問“為什么”。這樣才能引出學生更多的想法。如果教師的提問馬上能讓全體學生舉手回答，那不是好問題。主題式的數學名題往往是個大問題，能讓學生進入探究之中。

二、促使學生從低階思維邁向高階思維

“小先生學習模式”是最高品質的學習。基于“數學名題”經典的學習載體，通過學生“獨立自主研讀——小組交流合作探究——小先生匯報解說——同伴認真傾聽質問——全班師生多維互動研討”，不斷刺激學生的大腦，改變學生的線性思維，實現網狀聯結，形成高階思維。思維層次有高低之分，而思維方法沒有好壞之分，運用哪種思維方法解決什么問題卻有決策優劣之別。羅列出可解決問題的種種方法，選用最合理的思維方法解決問題，這是思維動態的決策能力。久而久之，這種思維能力漸漸成為不容易改變的一種慣性，即思維品質。思維的獨創性、靈活性、敏捷性、深刻性、批判性……影響學生一生的學習、工作與生活。這就是我們所要追求的學生的核心素養。不唯書，不唯師，不唯上的批判性思維的培養，能讓學生張開創造、想象的思維翅膀。

三、指導學生學會表示思考過程的方法

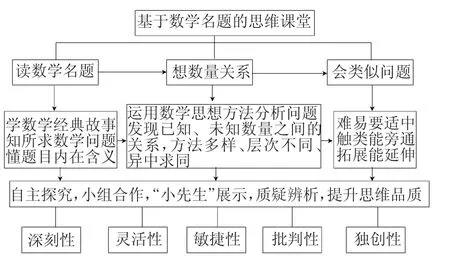
根據以上要素的理論分析與課堂實踐，筆者經過幾年來的總結，提煉形成了“基于數學名題的思維課堂”模式。

（一） 讀有價值的數學名題

“雞兔同籠”問題是我國民間廣為流傳的數學趣題，最早出現在《孫子算經》中，如今被編入到北師大版、蘇教版、人教版、北京版等不同版本不同年級的教材中。如何充分利用數學名題“雞兔同籠”在不同年級進行不同思維方法的有效引導呢？要遵循兒童的認知規律，科學合理地品讀數學名題。我們安排了三、四、五、六年級學生讓四位教師同課異構，根據各個層次的年齡特征定位不同的學習目標。三年級目標為畫圖策略；四年級的目標為從逐一列表假設拓展到跳躍列表假設；五年級的目標定位為靈活運用逐一、折中和跳躍假設法，并學會用兩步假設來推理出正確答案，過渡到算術假設法；六年級的目標則定位為方法上的求聯，通過比較畫圖、列表、算術推理、方程假設等各種方法，把所有的方法上升為一種假設的上位思想。學生思維發展由具體到抽象的過程顯露無疑，充分體現了雞兔同籠的思維價值。由此可見，不同年級確定不同目標，采用不同方法品讀數學名題，符合學生的認知特點，也能真正讀懂數學名題。

（二） 想已知與未知數量之間的關系

引導學生合理選用分析法、綜合法、假設法等數學思想方法發現數量之間的關系。《雞兔同籠》這一數學名題的關鍵是讓學生“自主探究、小組合作、小先生展示、質疑辨析”，引導學生在運用假設法的同時，要化無形的思維為有形思維，理清已知與未知之間的數量關系。思維本身就是無形的，如果教師能在實施過程中化無形為有形，勢必會讓學生的思維增量。如三年級的課中采用畫圖的策略來解決問題，針對畫圖一次不能到位而需要調整時，教師可用不同顏色的粉筆標出腳太多時把兔調整為雞，或者可以用圈的方法在旁邊標注調整的過程，這樣學生的思維過程就表達出來了。四年級的課中，學生出現圖1情況，教師應該適時地讓孩子回到雞兔畫圖的過程，來理解“腳少了怎么辦？加兔減雞。”

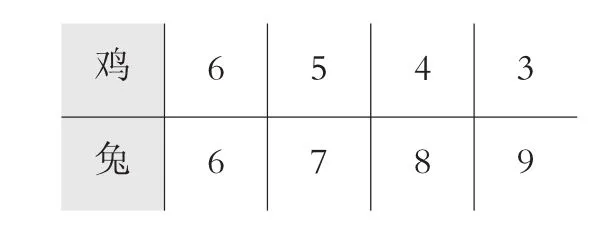
圖1

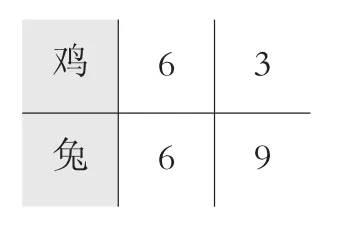
圖2

如圖2，學生的回答是通過2次折中假設得出正確答案，此時，教師可順勢質疑，為什么雞的只數再次取半，而不往上推理呢？因為腳數太少，要增加兔的數量，從而發展學生的邏輯推理能力。

五年級的課堂如圖3：通過教師的表格數據比對，調整過程用箭頭顯現，學生調整的過程一目了然，理解起來顯得輕松。兩步列表法發展到算術法只差臨門一腳，因此，通過兩步列表法理解過程，算術法來總結，思維過程就水到渠成了。

圖3

從課初的隨意猜想到表格中的有序猜想，從一般驗證到表格中數據變化規律的發現，從列表法自然聯想到假設法，學生的思維經歷了從無序到有序、從特殊到一般、從借鑒到創新、從膚淺到深刻的巨大變化，學生的思維能力也隨之得到了極大的提升。

（三） 能觸類旁通和拓展延伸

三、四、五年級的課堂中呈現了大量的素材，教師需要幫助學生舉一反三建立雞兔同籠的模型，如：日本的龜鶴算、三輪車和自行車同輪分配、人民幣混裝問題都屬于雞兔同籠模型下的思維拓展。面對這些問題，引導學生給“雞兔同籠”重新取名。不經意的點撥，適時的追問，讓學生一次次跳出那只有形的“籠子”，超越具體的解題方法，上升為一種更具有普適性的思想方法與策略——假設，從而建構起解決這類問題的更具有一般性的“數學模型”，通過方法遷移，會一題，通一類。

（作者單位：浙江省義烏復旦實驗學校）

（責任編輯：楊強）