計數原理、二項式定理單元過關測試
■福建省龍巖市永定區城關中學 童其林(特級教師)
計數原理、二項式定理單元過關測試
■福建省龍巖市永定區城關中學 童其林(特級教師)
一、選擇題(共12小題,每小題5分,共60分。在每個小題給出的四個選項中,只有一項是符合題目要求的)
1.n∈N*,則(20-n)(21-n)…(100-n)等于( )。
A.A80100-nB.A20-n100-n
C.A81100-nD.A8120-n
2.將甲、乙、丙、丁、戊5本不同的書擺成一排,若甲書與乙書必須相鄰,而丙書與丁書不能相鄰,則不同的擺法種數為( )。
A.48 B.24 C.20 D.12
3.一個盒子里有3個分別標有號碼1,2, 3的小球,每次取出1個,記下它的標號后再放回盒子中,共取3次,則取得小球標號最大值是3的取法有( )。
A.12種 B.15種
C.17種 D.19種
4.將5位同學分別保送到北京大學、上海交通大學、廈門大學這3所大學就讀,每所大學至少保送1人,則不同的保送方法共有( )。
A.150種 B.180種
C.240種 D.540種
5.若(2x-1)2016=a0+a1x+a2x2+… +a2016x2016,x∈R,則
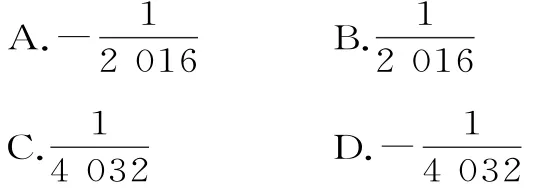
6.有10個乒乓球,將它們任意分成兩堆,求出這兩堆乒乓球個數的乘積,再將每堆乒乓球任意分成兩堆并求出這兩堆乒乓球個數的乘積,如此下去,直到不能再分為止,則所有乘積的和為( )。
A.45 B.55 C.10! D.1010
7.若x10=a0+a1(x-1)+a2(x-1)2+…+a10(x-1)10,則a8的值為( )。
A.-45 B.-9 C.10 D.45

圖1
8.如圖1所示,平面α中有梯形ABCD與梯形A1B1C1D1分別在直線l的兩側,它們與l無公共點,并且關于l對稱,現將α沿l折成一個直二面角,則A,B,C,D,A1,B1,C1,D18個點可以確定平面的個數是( )。
A.56 B.44 C.42 D.40
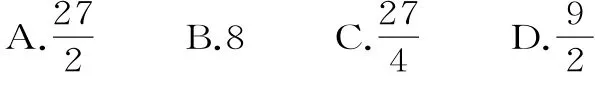
10.已知函數f(x),x∈1,2,3{},其函數值在集合1,2,3{}中,且滿足f(f(x))= f(x),則這樣的函數的共有( )。
A.1個 B.4個
C.8個 D.10個
11.我們把各位數字之和為6的四位數稱為“六合數”(如2013是“六合數”),則“六合數”中首位為2的“六合數”共有( )。
A.18個 B.15個
C.12個 D.9個
12.已知m是一個給定的正整數,如果兩個整數a,b除以m所得的余數相同,則稱a與b對模m同余,記作a≡b(modm)。例如,5≡13(mod4)。若22015≡r(mod7),則r可能等于( )。
A.2013 B.2014
C.2015 D.2016
二、填空題(本大題共四小題,每小題5分,共20分)
13.有3張標號分別為1,2,3的紅色卡片,3張標號分別為1, 2,3的藍色卡片,現將全部的6張卡片放在2行3列的格內(如圖2所示)。若顏色相同的卡片放在同一行,則不同的放法種數為____。(用數字作答)

圖2
14.已知(1+x)+(1+x)2+…+(1+ x)n=a0+a1x+a2x2+…+anxn,若a1+a2+…+an-1=29-n,則n=_____。
15.定義“自傳數”為滿足以下條件的自然數:第一位數(從左到右)是所有數位中“0”的個數,第二位數是所有位數中“1”的個數,第三位數是所有數位中“2”的個數,…(例6210001000是一個“自傳數”)。則最小的“自傳數”等于____。
16.已知n,k∈N*,且k≤n,,則可推出:

由此,可推出C1n+22C2n+32C3n+…+ k2Ckn+…+n2Cnn=____。
三、解答題(解答應寫出文字說明、證明過程或演算步驟,共70分)
17.(本小題滿分10分)
已知集合M={-3,-2,-1,0,1,2}, P(a,b)表示平面上的點,a,b∈M,問:
(1)P可表示平面上多少個不同的點?
(2)P可表示平面上多少個在第二象限內的點?
(3)P可表示多少個不在直線y=x上的點?
18.(本小題滿分12分)
解答下列各題:
(2)求證:3n>(n+2)·2n-1(n∈N*,n>2)。
19.(本小題滿分12分)
有4個不同的球,4個不同的盒子,把球全部放入盒內。
(1)共有多少種放法?
(2)如果恰有1個盒子不放球,有多少種放法?
(3)如果恰有1個盒子內放2個球,有多少種放法?
(4)恰有2個盒子不放球,有多少種放法?
20.(本小題滿分12分)
21.(本小題滿分12分)
已知數列{an}通項公式為an=Atn-1+ Bn+1,其中A,B,t為常數,且t>1,n∈N*。等式(x2+2x+2)10=b0+b1(x+1)+ b2(x+1)2+…+b20(x+1)20,其中bi(i=0, 1,2,…,20)為實常數。
22.(本小題滿分12分)
設A,B均為非空集合,且A∩B=?,A∪B=1,2,3,…,n
{ },n≥3,n∈N*。
記A,B中元素的個數分別為a,b,所有滿足“a∈B,且b∈A”的集合對(A,B)的個數為an。
(1)求a3,a4的值;
(2)求an。
1.C 2.B 3.D 4.A 5.C 6.A 解析:積為定值,可取特殊情況分析,10分為1和9,9再分為1和8,…,2再分為1和1,計算得值為45。
7.D 8.B 9.D
10.D 解析:當f(x)=x時,顯然滿足f(f(x))=f(x),此時有一個這樣的函數,即若f(1),f(2),f(3)中有兩個為同一個值,一個為f(1)=1,或f(2)=2,或f(3)=3,也滿足:
11.B 12.A 13.72 14.4 15.1210 16.n(n+1)·2n-2
17.(1)確定平面上的點P(a,b)可分兩步完成:第一步確定a的值,共有6種確定方法;第二步確定b的值,也有6種確定方法。根據分步計數原理,得到所求點的個數是6×6=36(個)。
(2)確定第二象限的點,可分兩步完成:第一步確定a,由于a<0,所以有3種確定方法;第二步確定b,由于b>0,所以有2種確定方法。由分步計數原理,得到第二象限的點的個數是3×2=6(個)。
(3)點P(a,b)在直線y=x上的充要條件是a=b。因此a和b必須在集合M中取同一元素,共有6種取法,即在直線y =x上的點有6個。結合(1)可得不在直線y=x上的點共有36-6=30(個)。
18.(1)由組合數的性質可得:
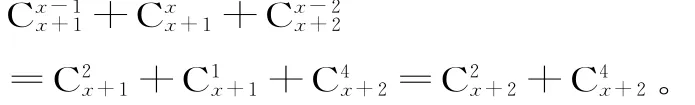
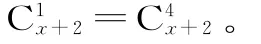
4=x+2-1,x=3。經檢驗知x=3符合題意,所以x=3。
(2)證明:因為n∈N*,且n>2,所以3n=(2+1)n展開后至少有4項。
(2+1)n=2n+C1n·2n-1+…+Cn-1n· 2+1≥2n+n·2n-1+2n+1>2n+n·2n-1=(n+2)·2n-1,故3n>(n+2)·2n。
19.(1)1個球1個球地放到盒子里去,每只球都可有4種獨立的放法,由分步乘法計數原理,放法共有:44=256(種)。
(2)為保證“恰有1個盒子不放球”,先從4個盒子中任意拿出1個,即將4個球分成2,1,1的三組,有C24種分法;然后再從3個盒子中選1個放2個球,其余2個球,2個盒子,全排列即可。共有放法: C14C24C13A22=144(種)。
(3)“恰有1個盒內放2個球”,即另外3個盒子中恰有1個空盒。因此,“恰有1個盒內放2球”與“恰有1個盒子不放球”是一回事,也有144種放法。
(4)先從4個盒子中任意拿走2個,有C24種方法,問題轉化為:“4個球,2個盒子,每盒必放球,有幾種放法?”從放球數目看,可分為(3,1),(2,2)兩類。第一類:可從4個球中先選3個,然后放入指定的1個盒子中即可,有C34C12種放法;第二類:有C24(種)放法。因此共有C34C12+C24=14種。由分步乘法計數原理得“恰有2個盒子不放球”的放法有:C24·14=84(種)。也可這樣求解:確定2個空盒有C24種方法。4個球放進2個盒子可分成(3,1),(2,2)兩類,第一類為有序不均勻分組,有C34C11A22種放法,第二類為有序均勻分組,有種放法,故共有84(種)放法。
20.由題意知,22n-2n=992。
即(2n-32)(2n+31)=0。
解2n=32,得n=5。
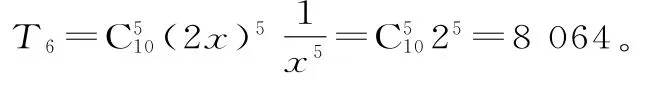
(2)設第r+1項的系數最大。
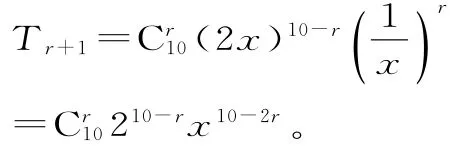
因為r∈N*,所以r=3。故系數最大的項是第4項,T4=15360x4。
21.(1)(x2+2x+2)10=(1+(x+1)2)10
=C010+C110x+1()2+C210x+1()4+…+ C1010x+1()20
=b0+b1x+1()+b2x+1()2+…+ b20x+1()20。
比較可知:b2n=Cn10,n=1,2,…,10。
而A=0,B=1時,an=n+1。
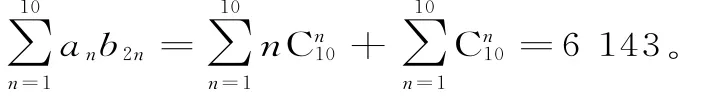
(2)當A=1,B=0時,an=Atn-1+Bn+ 1=tn-1+1,結合①中結論可知:
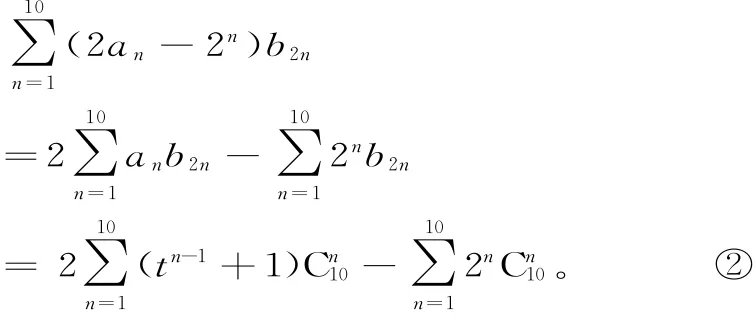
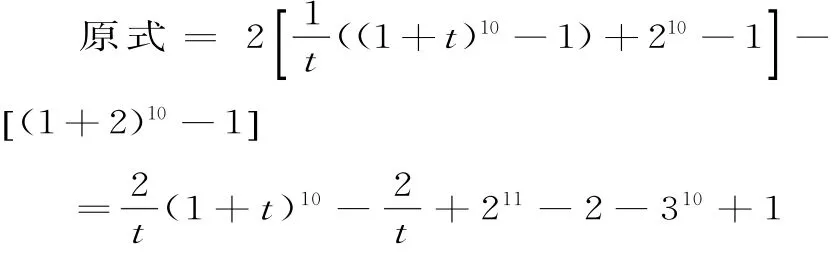
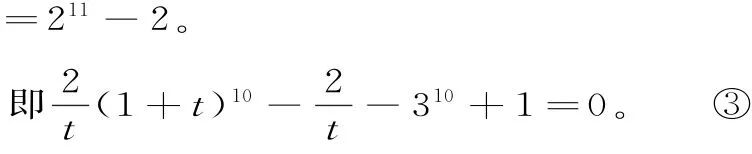
因為②為關于t的遞增的式子,所以關于t的方程最多只有一解,而觀察③可知,有一解t=2,綜上可知t=2。
22.(1)當n=3時,A∪B={1,2,3},且A∩B=?。若a=1,b=2,則1∈B,2∈A,有C01種情況;若a=2,b=1,則2∈B,1∈A,共有1種情況,所以a3=2。
當n=4時,A∪B={1,2,3,4},且A∩ B=?,若a=1,b=3,則1∈B,3∈A,有種情況;若a=2,b=2,則2∈B,2∈A,這與A∩B=?矛盾;若a=3,b=1,則3∈B,1∈A,共有C22種情況,所以a4=C02+C22=2。
(2)當n為偶數時,A∪B={1,2,3,…, n},且A∩B=?。
若a=1,b=n-1,則1∈B,n-1∈A,共C0n-2種(考慮A);
若a=2,b=n-2,則2∈B,n-2∈A,共C1n-2種(考慮A);
…
A∩B=?矛盾;
…
(責任編輯 徐利杰)

