基于改進二維分形模型的海面模擬方法

何四華，吳春光，叢 濱

(中國人民解放軍92941部隊 91分隊， 遼寧 葫蘆島 125000)

【基礎理論與應用研究】

基于改進二維分形模型的海面模擬方法

何四華，吳春光，叢 濱

(中國人民解放軍92941部隊 91分隊， 遼寧 葫蘆島 125000)

針對粗糙海面的非線性和自相似性特點，在帶限Weierstrass分形函數的基礎上，建立了改進二維分形模型，描述了表面譜與空間波數之間的正冪率和負冪率關系，針對P-M海譜給出了分形參數的定量描述，實現了對粗糙海面的模擬。仿真結果表明，模型能夠生成不同風速下的海面模型，反映了小尺度波浪的細微結構和大尺度波浪的浪涌特性，不同尺度的組成波之間具有較好的自相似性，可以較好地模擬粗糙海面背景。

Weierstrass分形函數；P-M海譜；改進二維分形模型；粗糙海面

海面背景下艦船目標的電磁散射特性是反艦武器系統試驗鑒定結果評定的重要依據，也是水面靶標設計的基礎。幾何建模是電磁散射特性仿真分析的基礎和前提，幾何模型的可靠性和建模精度直接決定了電磁散射計算的精度。除了艦船目標外，如何精確地建立粗糙海面背景的幾何模型是電磁散射特性仿真分析的重要前提[1]。由于影響海面形態的動力因素復雜多變，建立一個完全準確的數學模型十分困難，因此海面模擬的方法通常都是基于一定的假設前提，而且諸多技術仍處于發展中。由于實際海面具有非線性和自相似性等分形結構的特點，基于分形理論實現對粗糙海面的建模具有獨特的優勢。

1 海面狀態的描述

為了研究粗糙海面的幾何特征，需要了解海浪的形成過程、影響海面形狀變化的動力因素和海面狀態的描述方式。有3種數值方式描述海面狀態[2]，分別是Doglsas級數、國際氣象組織(WMO)代碼75和蒲福風級。其中Doglsas級數應用廣泛，但后來被WMO代碼75代替了，而蒲福風級是用風速來劃分海面狀態。表1所示為Doglsas級數和WMO的劃分尺度，表2為蒲福風級的劃分尺度。

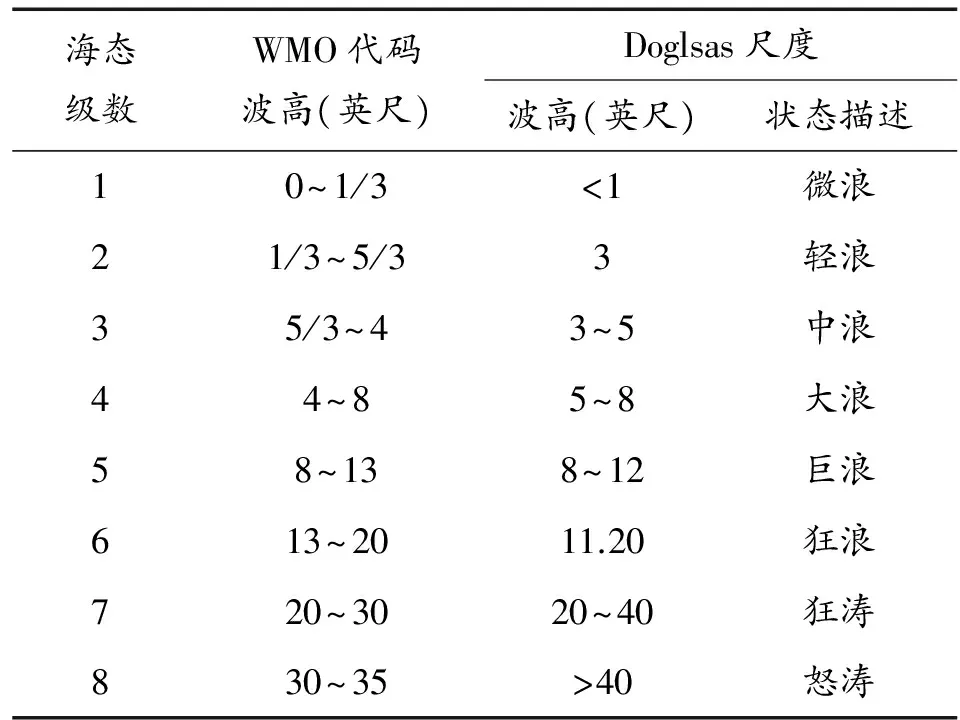
表1 WMO和Doglsas劃分尺度

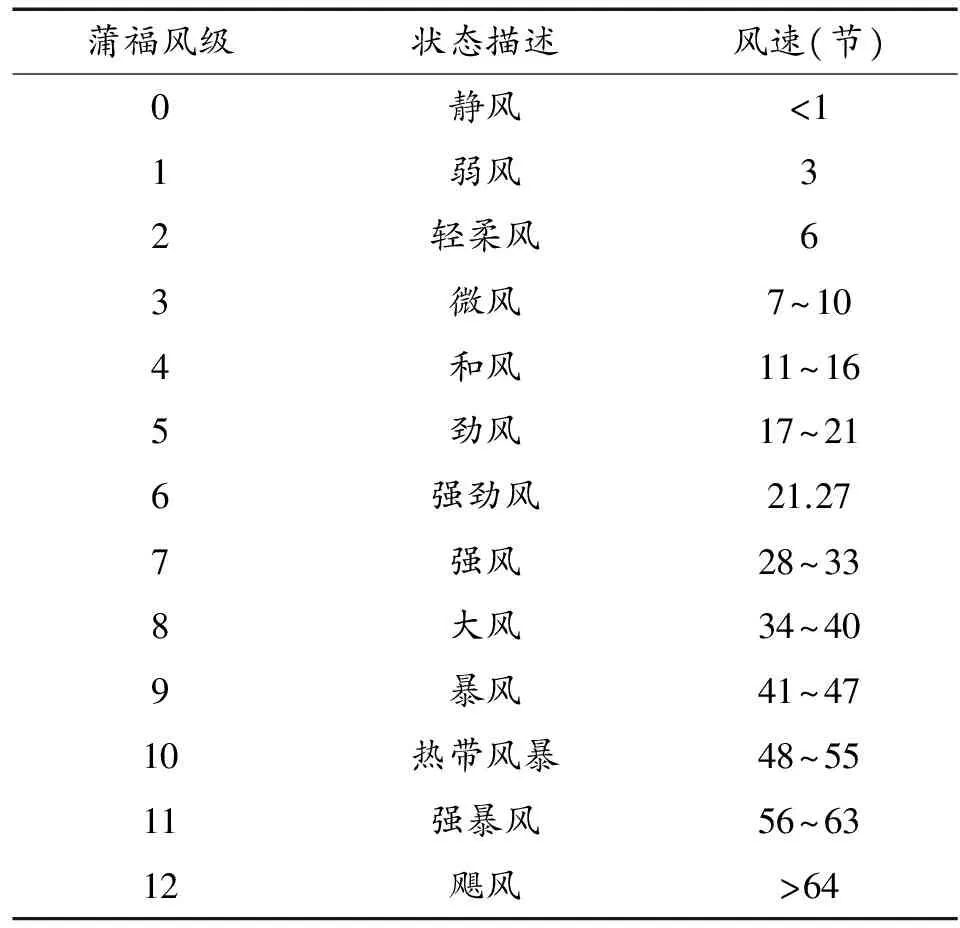
表2 蒲福風級的劃分尺度

2 海面模擬

海面可視作由無限多個振幅不同、頻率不同、方向不同、相位雜亂的海浪波組成的隨機過程。海譜是功率譜，代表海浪能量相對于組成波各空間頻率或各空間波數的分布，已經成為模擬海面的基礎和檢驗標準[3]。

2.1 海譜

將海浪視為隨機過程，通過海譜來描述海浪已成為主要的研究途徑，因此確定譜的形式是研究隨機海浪的重要內容。海譜可表示為頻譜S(ω)或者波數譜S(k)，它們之間滿足如下關系

(1)

其中，σ2是海面相對于參考面的均方根。

對于二維海面，功率譜不僅與頻率(波數)有關，還與方向有關。引入角度分布函數后，功率譜是二維的，稱為方向譜。方向譜的表示形式有S(ω,θ)，S(k,θ)和S(kx=kcosθ,ky=ksinθ)，其中θ為觀測方向與逆風方向之間的夾角。這3種方向譜滿足如下關系

(2)

忽略波浪間的非線性相互作用，海水中k和ω的關系式為

(3)

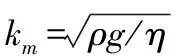
完成年度公益性水利工程維修養護資金合規性審核。對24個中西部地區、貧困地區省份的縣級國有管理單位及其所屬單位申報的2013年度中央財政補助資金項目，從項目范圍、項目類別、維修養護內容、維修養護經費等方面進行合規性審核，涉及承擔防洪、排澇、抗旱、灌溉等公益性任務的水庫、水閘、堤防、控導工程、泵站、淤地壩等6類工程6 000多個項目。

(4)

海譜可分為重力波譜和張力波譜。到目前為止，眾多學者已提出了多種形式的海譜模型。其中，P-M譜是一種比較經典且應用廣泛的重力波譜；Fung的半經驗海譜是最早的完全海譜(包含重力波和張力波)，根據該譜模型計算出的散射結果與測量值吻合較好；D-B-J譜是一種最新的完全海譜，并且有效地區分了順風和逆風的情形；JONSWAP譜是一種非穩態海譜，被認為是國際標準海洋譜。

2.2 帶限Weierstrass分形函數的海面模擬

自1982年Mandelbrot首次提出“分形”的概念后，分形理論在眾多領域內得到了廣泛應用。由于實際海面具有非線性和自相似性等分形結構的特點[4]，因此，不少學者近年來開始研究模擬海面的分形模型。通常用經典的帶限Weierstrass分形函數來模擬二維動態海面，該模型表示為

(5)

式中：σ為海面的高度起伏均方根；C為歸一化因子；Nf為諧波數量；s是分形模型的分維數(21)；K0為海表面的空間基波數；θn為主方向角；βn(t)為相對于主方向角(風向)的偏角；Ωn為第n個譜分量的圓頻率；φn是[-π,π]上均勻分布的隨機相位；Vx和Vy分別是雷達平臺沿x和y方向的運動速度。

可見，該分形模型需要設置的參數較多，約束關系復雜，參數的變化可直接在該譜的變化中反映出來，可較好地反映海面的實際情況。但該模型表面譜與空間波數之間僅包含負冪率部分[5]，而實際海面既包括正冪率部分又包括負冪率部分，因此只能部分與海譜模型吻合。

針對帶限Weierstrass分形函數模型存在的問題[6]，提出了一種改進的二維分形模型，增加了表面譜與空間波數之間正冪率部分的描述，并通過推導對各項參數進行了定量說明。改進后的模型表示為

(6)

可見，改進后的模型在原有模型等式右邊新增了一項，保留項中所有參數定義與原有模型一致[7]。受新增項的影響，歸一化因子C表示為

(7)

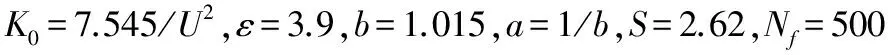
3 仿真分析

3.1 仿真方法

1) 設定海面大小，劃分波面網格；

2) 選定海譜，對頻率空間和方向空間進行分割離散，求出不同頻率和不同方向下的波幅；

3) 根據式(6)確定波浪的造型；

4) 設定時間步長Δt，依次改變時間t，得到時變動態海面。

3.2 仿真結果

采用P-M海譜和改進二維分形模型等兩種方法進行動態海面生成,分別設置風速U=2 m/s,U=4 m/s和U=6 m/s, 結果如圖1～圖3所示，其中圖1(c)、圖2(c)、圖3(c) 均為動態海面中的一組抽樣數值。

統計3種條件下的實驗數據，對P-M海譜和改進二維分形模型生成的動態海面進行均值和方差統計，比較分析模型的一致性，對動態海面的抽樣數據的拐點數進行統計，比較分析模型對動態海面細節的描述程度，結果如表3所示。

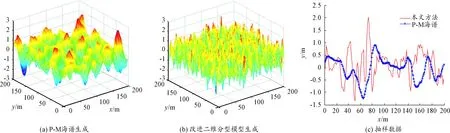
圖1 風速U=2 m/s條件下生成的動態海面

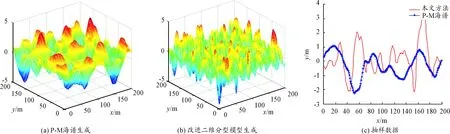
圖2 風速U=4 m/s條件下生成的動態海面

圖3 風速U=6 m/s條件下生成的動態海面

方法風速U=2m/s均值方差拐點數風速U=4m/s均值方差拐點數風速U=6m/s均值方差拐點數P?M海譜00．60151201．1670902．33259改進二維分形模型00．58393501．15892101．982614

3.3 數據分析

數據結果分析對比表明：

1) 改進二維分形模型和P-M海譜生成動態海面高度的均值和方差比較接近，表明兩種動態海面生成模型具有較好的一致性。

2) 相同風速條件下，改進二維分形模型能夠更好地表現小尺度波浪細微結構的動態變化，生成動態海面的細節信息較P-M海譜豐富，可以取得較好的模擬效果。

3) 隨著風速增大，海面大尺度波開始起主導作用，小尺度波漸漸被忽略，能夠更好地表現大尺度波浪的浪涌特性，動態海面也表現出了很明顯的分形特點，即不同尺度的組成波之間的自相似性。

4 結論

提出了一種基于改進二維分形模型的海面模擬方法，更好地描述了表面譜與空間波數之間的負冪率部分和正冪率部分，給出了分形模型的具體參數，與P-M海譜進行了比對，仿真結果表明分形方法更加具體的表達了粗糙海面的非線性幾何特性。模型與實際測量結果的吻合程度需要大量的數據進行驗證，這項工作有待后續開展。

[1] 方重華.復雜的二維海面電磁散射模型[J].哈爾濱工程大學學報,2008,29(8):779-782.

[2] 齊國雷,周東方,饒育萍,等.FDTD方法分析高功率微波粗糙地面散射特性[J].強激光與粒子束,2010,22(9):2092-2096.

[3] 郭立新，官秀國，徐英霞.分形粗糙面單站散射的遮蔽效應研究[J].西安電子科技大學學報,2003,30(5):617-622.

[4] 陳勇,侯德亭,齊國雷,等.分形海面電磁散射特性的基爾霍夫近似[J].信息與電子工程,2009,7(5):409-412.

[5] 王運華,郭立新,吳振森.改進的一維分形模型在海面電磁散射中的應用[J].電子學報,2007,35(3):478-483.

[6] 侯德亭,宋航,陳勇,等.分形海面的微波電磁散射計算模型[J].強激光與粒子束,2010,22(9):2119-2123.

[7] 楊俊嶺,郭立新,萬建偉.基于未充分發展海譜的分形海面模型及其電磁散射研究[J].物理學報,2007,56(4):2106-2114.

(責任編輯 唐定國)

Simulation Method of Sea Surface Based on Improved Two-Dimensional Fractal Model

HE Si-hua, WU Chun-guang, CONG Bin

(91 Element of No.92941stTroop of PLA, Huludao 125000, China)

According to the nonlinear and self-similarity characteristics of rough surface, based on the band-limited Weierstrass fractal function, the improved two-dimensional fractal model was set up, and the relationship between the positive power and negative power of surface spectrum and space wave number was described. According to that P-M sea spectrum the quantitative description of fractal parameters was given, the simulation of rough sea surface was realized. Simulation results indicated that the model can generate the surface of the model under different wind speed, and the fine structure of small scale waves and the surge characteristics of large scale waves were showed, and the composition of the different scale had a good self-similarity between wave, which could better simulate the rough sea surface background.

Weierstrass fractal function; P-M sea spectrum; the improved two-dimensional fractal model; rough sea surface

2016-12-26；

2017-01-25 基金項目：國家自然科學基金資助項目(61673129)

何四華(1979—)，男，博士，主要從事目標特性、非線性信號處理研究。

10.11809/scbgxb2017.05.036

format:HE Si-hua, WU Chun-guang, CONG Bin.Simulation Method of Sea Surface Based on Improved Two-Dimensional Fractal Model[J].Journal of Ordnance Equipment Engineering,2017(5):155-158.

TP15

A

2096-2304(2017)05-0155-04

本文引用格式：何四華,吳春光,叢濱.基于改進二維分形模型的海面模擬方法[J].兵器裝備工程學報，2017(5):155-158.