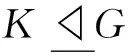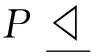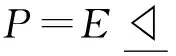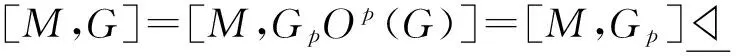弱S-嵌入子群與有限群的p-冪零性

郭桂容，趙 濤，陳云坤

(1.貴州商學(xué)院基礎(chǔ)部，貴州 貴陽 550014；2.六盤水師范學(xué)院數(shù)學(xué)系，貴州 六盤水 553004；3.山東理工大學(xué)理學(xué)院，山東 淄博 255049；4.貴州師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，貴州 貴陽 550001)

弱S-嵌入子群與有限群的p-冪零性

郭桂容1，2，趙 濤3，陳云坤4

(1.貴州商學(xué)院基礎(chǔ)部，貴州 貴陽 550014；2.六盤水師范學(xué)院數(shù)學(xué)系，貴州 六盤水 553004；3.山東理工大學(xué)理學(xué)院，山東 淄博 255049；4.貴州師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院，貴州 貴陽 550001)

研究了群G的某些弱S-嵌入子群對其p-冪零性的影響，得到了幾個新結(jié)果，同時也推廣了原有的一些眾所周知的結(jié)論.

s-可換子群；弱S-嵌入子群；p-冪零群；群系

1 預(yù)備知識

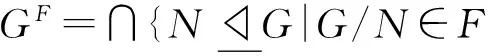
定義1.1[14]G的子群H稱為是弱S-嵌入于G的，如果G有正規(guī)子群T滿足HT是G的s-置換子群且H∩T≤Hse，其中Hse表示G的包含在H中的s-置換嵌入子群.

文獻(xiàn)[13-14]得到了一些關(guān)于G的弱S-置換子群的有趣結(jié)果，本文繼續(xù)研究弱S-置換子群對G的p-冪零性的影響并推廣了一些現(xiàn)有結(jié)果.

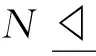
(1) 如果H≤K≤G，則H在K中是s-置換的；

(2) 如果HN與H∩N在G中s-置換，則HN/N在G/N中s-置換；

(3)H是G的次正規(guī)子群；

(4) 如果H是一個p-群，則NG(H)≥Op(G).

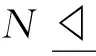
(1) 如果H≤K，則H是K的s-置換嵌入子群；

(2)HN是s-置換嵌入于G的，且HN/N是s-置換嵌入于G/N.

引理1.3[15]假設(shè)H是s-置換于G的，P是H的Sylowp-子群，其中p是素數(shù).如果HG=1，則P是s-置換于G的.

引理1.4[14]設(shè)G是群且H≤K≤G.那么：

(1) 若H是G的正規(guī)子群，則K/H是G/H的弱S-置換子群，當(dāng)且僅當(dāng)K是G的弱S-嵌入子群；

(2) 如果H是弱S-置換于G的，則H弱S-置換于K；

(3) 假設(shè)H是G的正規(guī)子群，那么對于G的每個滿足(|H|，|N|)=1的弱S-嵌入子群N，NH/H弱S-置換于G/H；

(4) 如果H弱S-置換于G且K是G的正規(guī)子群，那么G有包含在K中的正規(guī)子群T，滿足HT是S-置換于G且H∩T≤Hse.

引理1.5[16]設(shè)G是一個群且p是一個滿足pn+1|G|的素數(shù).對某個n≥1，如果(|G|，(p-1)(p2-1)…(pn-1))=1，則G是p-冪零的.

2 主要結(jié)果

定理2.1設(shè)P是G的Sylowp-子群，其中p是|G|的素因子，且(|G|，(p-1)(p2-1)…(pn-1))=1.如果P的每個在G中無p-冪零補的n-極大子群(如果存在)都弱S-嵌入于G，則G是p-冪零的.

證明 假設(shè)結(jié)論錯誤并設(shè)G是極小階反例.分以下幾步證明：

(1) |P|≥pn+1且P的每個n-極大子群都是弱S-嵌入于G的.

由引理1.5，假設(shè)|P|≥pn+1.如果存在P的n-極大子群P1在G中有冪零補T，則說明G是p-冪零的.否則，設(shè)H是G的包含P的非p-冪零子群且H的每個真子群是p-冪零的，那么由文獻(xiàn)[5]之定理5.4，H是極小非冪零群.從而H有以下性質(zhì)：

(ⅰ) |H|=paqb，其中p與q是不同素數(shù)；

(ⅱ)H=[Hp]Hq，其中Hp=P是H的正規(guī)Sylowp-子群，且Hq是H的循環(huán)Sylowq-子群；

(ⅲ)P/φ(P)是H的主因子.

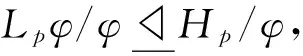
(2)G不是一個非交換單群.

由步驟(1)的結(jié)果可知P有非平凡的n-極大子群P1弱S-嵌入于G，于是存在G的正規(guī)子群T使得P1T在G中是s-置換的，且P1∩T≤(P1)se.如果G是一個非交換單群，則T=1或G.如果T=1，那么P1=P1T在G是s-置換的，從而P1是G的次正規(guī)真子群，矛盾.故T=G，從而P1=(P1)se是s-置換嵌入G，P1是某個s-置換嵌入子群K的Sylowp-子群，K在G中次正規(guī).因為G是單群，于是K=G且P1是G的Sylowp-子群，矛盾.故G不是非交換單群.

(3)G有唯一一個極小正規(guī)子群N且φ(G)=1.

設(shè)N是G的一個極小正規(guī)子群，證明假設(shè)對于G/N仍成立.如果G/N的Sylowp-子群PN/N是循環(huán)的，那么由文獻(xiàn)[17]之引理2.2知G/N是p-冪零的，因此假設(shè)PN/N是非循環(huán)的且|PN/N|≥pn+1，從而P是非循環(huán)的.設(shè)M/N是PN/N的一個n-極大子群，易知存在P的n-極大子群P1使得M=P1N，且P∩N=P1∩N是N的Sylowp-子群.由假設(shè)與結(jié)論(1)，可設(shè)P1弱S-置換于G，從而存在G的正規(guī)子群T使得P1T是s-置換于G且P1∩T≤(P1)se.顯然，TN/N在G/N中正規(guī)且P1N/N，TN/N=P1TN/N在G/N中是s-置換的.注意到P1∩N是N的Sylowp-子群，所以

|(P1∩N)(T∩N)|p=|P1∩N|=|N|p=|N∩P1T|p.

由P1是p-群，則

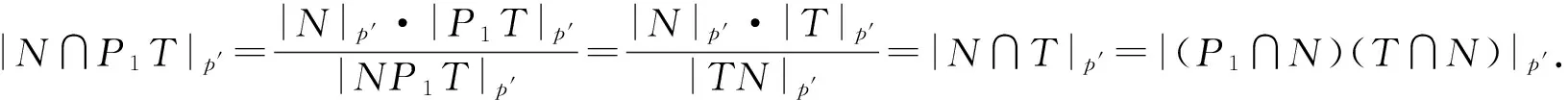
上面兩式意味著(P1∩N)(T∩N)=P1T∩N，于是由文獻(xiàn)[18]可知P1N∩TN=(P1∩T)N.由引理1.2，P1N/N∩TN/N=(P1∩T)N/N≤(P1)seN/N是s-置換于G/N的，因此M/N弱S-置換于G/N，從而G/N滿足定理假設(shè)，再由G的選擇知G/N是p-冪零的.因為所有p-冪零群類是飽和群系，所以N是G的唯一極小正規(guī)子群且φ(G)=1.

(4)Op′(G)=1.

如果Op′(G)≠1，那么N≤Op′(G)，且由結(jié)論(3)知G/Op′(G)是p-冪零的，因此G是p-冪零的，矛盾.

(5)Op(G)=1且N不是p-冪零的.

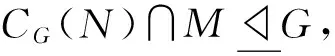
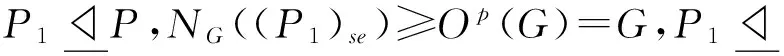
(6)G=PN.

由引理1.4，PN滿足定理假設(shè).由G的選擇可知如果PN

最后，如果P∩N≤φ(P)，那么由Tate定理[1]可知N是p-冪零的，與結(jié)論(5)矛盾.因此，存在P的極大子群P1滿足P=(N∩P)P1.設(shè)P2是P的包含在P1中的n-極大子群，因為P2弱S-嵌入于G，故存在G的正規(guī)子群T使得P2T是s-置換于G且P2∩T≤(P2)se.

如果T=1，則P2是s-嵌入于G的，因此Op(G)≠1，與結(jié)論(5)矛盾.于是可設(shè)T≠1且N≤T.如果(P2)se=1，則|T|p≤pn，由引理1.5知T是p-冪零的，N也是p-冪零的，這個矛盾說明(P2)se≠1.從而存在G的s-置換子群K使得(P2)se是K的Sylowp-子群.如果KG≠1，則N≤KG≤K且(P2)se∩N是N的Sylowp-子群.另一方面，P∩N是N的Sylowp-子群且(P2)se∩N≤P∩N，則(P2)se∩N=P∩N.這意味著P=(N∩P)P1=P1，矛盾.因此，KG=1.由引理1.3知(P2)se是G的s-置換子群，(P2)se≤Op(G)，與結(jié)論(5)矛盾.定理證畢.

定理2.2 設(shè)p是|G|的素因子且P是G一個p-子群.如果NG(P)是p-冪零群，且P的每個在G中無p-冪零補的極大子群都弱S-嵌入于G，則G是p-冪零群.

證明 如果p=minπ(G)，由定理2.1知G是p-冪零的，故只需考慮p不是G的最小素因子(因而是奇數(shù))的情況.假設(shè)結(jié)論不真且設(shè)G為極小階反例，則：

(1)P的每個極大子群都是弱S-嵌入于G的.

類似于定理2.1步驟(1)的證明.

(2)Op′(G)=1.

假設(shè)Op′(G)≠1，考慮G/Op′(G).顯然POp′(G)/Op′(G)是G/Op′(G)的Sylowp-子群且NG/Op′(G)(POp′(G)/Op′(G))=NG(P)Op′(G)/Op′(G)是p-冪零群.設(shè)T/Op′(G)是POp′(G)/Op′(G)的極大子群，則對于P的某個極大子群P1，T=P1Op′(G).由結(jié)論(1)與引理1.4之結(jié)論(3)，P1Op′(G)/Op′(G)弱S-嵌入于G/Op′(G)，從而G/Op′(G)滿足定理的假設(shè).于是由歸納法，G/Op′(G)是p-冪零的，從而G是p-冪零的，矛盾.

(3) 如果M是G的包含P的真子群，則M是p-冪零的.

因為NM(P)≤NG(P)是p-冪零的，由結(jié)論(1)與引理1.4之結(jié)論(1)，M滿足定理假設(shè)，從而G的極小性意味著M是p-冪零群.

(4)G=PQ可解且1

因為G不是p-冪零群，由Thompson定理[19]，存在P的非平凡特征子群H使得NG(H)不是p-冪零群.因為NG(P)是p-冪零的，選擇H使得NG(H)不是p-冪零，但對P的包含H的每個特征子群K，NG(K)是p-冪零的.顯然Ng(P)≤NG(H)，則由結(jié)論(3)，NG(H)=G.故H≤Op(G)≠1且Op(G)

(5)G有唯一極小正規(guī)子群N滿足G=[N]M，其中M是G的極大子群且N=Op(G)=F(G).

設(shè)N是G的極小正規(guī)子群，那么由結(jié)論(2)與(4)，N是初等交換p-群且N≤Op(G).容易看到G/N滿足假設(shè)，G的極小性的意味著G/N是p-冪零群.因為所有p-冪零群類是飽和群系，所以N是G的唯一正規(guī)子群且N≤≠φ(G)，結(jié)論(5)成立.

(6) |N|=p.

定理2.3 設(shè)p是一個素數(shù)，F(xiàn)是包含所有p-冪零群類Np的飽和群系，G是一個群且對某個整數(shù)n≥1滿足(|G|，(p-1)(p2-1)…(pn-1))=1.則G∈F，當(dāng)且僅當(dāng)G有正規(guī)子群E滿足G/E∈F，且對E的某個Sylowp-子群P，P的每個在G中無p-冪零補的n-極大子群-如果存在)都弱S-嵌入于G.

必要性是顯然的，下證充分性.假設(shè)結(jié)論錯誤且G是極小階反例.顯然(|E|，(p-1)(p2-1)…(pn-1))=1，且對于P∈Sylp(E)的每個n-極大子群H，或者H在E有p-冪零補，或者H是弱S-嵌入于E的.由定理2.1知，E是p-冪零群，E∈F.設(shè)T是E的正規(guī)p-補，則T在G中正規(guī).現(xiàn)將證明分成如下幾步：

(1)T=1.

如果T≠1，則斷言G/T(關(guān)于E/T)滿足定理假設(shè).事實上，(G/T)/(E/T)?G/E∈F.設(shè)H/T是PT/T=E/T的任意n-極大子群，則存在P的n-極大子群L滿足H=LT.由假設(shè)，或者L在G中有一個p-冪零補K，或者L弱S-嵌入于G.這意味著或者H/T=LT/T在G/T中有一個p-冪零補KT/T，或者H/T弱S-嵌入于G/T，故G/T滿足定理的假設(shè).G的階的極小性意味著G/T∈F.如果f與F分別是Np與F的典型定義，因為T是G的正規(guī)p′-子群，所以對G的任何主因子Ti+1/Ti，其中Ti≤T，有G/CG(Ti+1/Ti)∈f(q)，且每個整除于jTi+1=Tij的q，因為NpμF，f(q)μF(q)，由文獻(xiàn)[18]之命題3.11，G/CG(Ti+1/Ti)∈F(q).故由G/T∈F得G∈F，矛盾.從而T=1.

(2)CG(P)≥Op(G).

[1] HUPPERT B.Endliche gruppen[M].New York：Springer，1967：110-115.

[2] GORENSTEIN D.Finite groups[M].New York：Chelsea，1968：89-93.

[3] KEGEL O H.Sylow-gruppen und sbnormalteiler endlicher gruppen[J].Math Z，1962，78：205-221.

[4] DESKINS W E.On quasinormal subgroups of finite groups[J].Math Z，1963，82(2)：125-132.

[5] BALLESTER A，BOLINCHES M C， PEDRAZA-AGUILERA.Sucient conditions for supersolvability of finite groups [J].J Pure Appl Algebra，1998，127：113-118.

[6] WEI H，WANG Y.Onc*-normality and its properties[J].J Group Theory，2007，10：211-223.

[7] SKIBA A N.On weaklys-permutable subgroups of finite groups [J].J Algebra，2007，315：192-209.

[8] LI Y，QIAO S，WANG Y.On weaklys-permutably embedded subgroups of finite groups[J].Commun Algebra，2009，37：1086-1097.

[9] ZHAO T，LI X，XU Y.Weaklys-supplementally embedded minimal subgroups of finite groups[J].P Edinburgh Math Soc，2011，54：799-807.

[10] GUO W，WANG Y，SHI L.Nearlys-normal subgroups of finite group[J].J Alg Disc Struc，2008，6(2)：95-106.

[11] GUO W，SHUM K P，SKIBA A N.On solubility and super solubility of some classes of finite groups [J].Sci China Ser A，2009，52(2)：272-286.

[12] WANG Y，GUO W.Nearlys-normality of groups and its properties[J].Commun Algebra，2010，38：3821-3836.

[13] MALINOWSKA I A.Finite groups withsn-embedded ors-embedded subgroups[J].Acta Math Hung，2012，136(1)：76-89.

[14] LI J，CHEN G，CHEN R.On weaklyS-embedded subgroups of finite groups[J].Sci China Math，2011，54(9)：1899-1908.

[15] LI Y，WANG Y，WEI H.Onp-nilpotency of finite groups with some subgroupsπ-quasinormally embedded[J].Acta Math Hung，2005，108(4)：283-298.

[16] GUO W，SHUM K P，XIE F.Finite groups with some weaklys-supplemented subgroups [J].Glasgow Math J，2011，53：211-222.

[17] WEI H，WANG Y.Thec-supplemented property of finite groups[J].Proc Edinburgh Math Soc，2007，50：493-508.

[18] DOERK K，HAWKES T.Finite soluble groups[M].New York：Walter de Gruyter，1992：114-115.

[19] ROBINSON D J S.A course in the theory of groups [M].New York：Springer-Verlag，1993：115-117.

(責(zé)任編輯：李亞軍)

On thep-nilpotency and weaklyS-embedded subgroups of finite groups

GUO Gui-rong1，2，ZHAO Tao3，CHEN Yun-kun4

(1.Department of Basic Course，Guizhou University of Commerce，Guiyang 550014，China；2.Mathematics Department，Liupanshui Normal University，Liupanshui 553004，China；3.School of Sciences，Shandong University of Technology，Zibo 255049，China；4.School of Mathematics Science，Guizhou Normal University，Guiyang 550001，China)

The influence of some weaklyS-embedded subgroups on thep-nilpotency of a finite groupGis investigated.Some new results are obtained which generalize some known results.

s-permutable subgroup；weaklyS-embedded subgroup；p-nilpotent group；formation

1000-1832(2017)02-0006-05

10.16163/j.cnki.22-1123/n.2017.02.002

2015-09-22

國家自然科學(xué)基金資助項目(11171243)；貴州省科學(xué)技術(shù)基金資助項目(黔科合J字LKLS[2013]31號).

郭桂容(1974—)，女，教授，主要從事基礎(chǔ)代數(shù)的教學(xué)和研究；通信作者：趙濤(1981—)男，博士，主要從事群論研究.

O 152 [學(xué)科代碼] 110·21

A