時間分數階KdV方程的級數解
高憶先,李金玉,徐 飛
(東北師范大學數學與統計學院,吉林 長春 130024)
時間分數階KdV方程的級數解
高憶先,李金玉,徐 飛
(東北師范大學數學與統計學院,吉林 長春 130024)
主要考慮Riemann-Liouville積分和Caputo導數意義下的分數階KdV方程初值問題,通過一類迭代法構造分數階KdV 方程在實數域上的級數解,并將這類迭代法推廣到復空間上,建立了分數階KdV方程在復數域上的級數解.這類迭代法只依賴于初值的選取,對于非線性分數階偏微分方程,甚至是耦合系統,都能有效地建立級數解.
時間分數階KdV方程;Riemann-Liouville積分;Caputo導數;迭代法;級數解
0 引言
1895年,荷蘭數學家 Korteweg和de Vries在研究淺水中小振幅長波運動時共同發現了一種單向運動淺水波偏微分方程
(1)
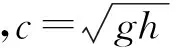
這就是歷史上經典的Korteweg-de Vries方程,簡稱KdV方程.[1]近年來由于在電磁學、光學、彈性力學、電子化學、材料科學等領域有很多現象均由分數階微分方程描述,因此尋找分數階微分方程的數值解和近似解成為了眾多學者的研究目標.[2-3]雖然關于經典的KdV方程目前已經有了大量的、有意義的成果,但對于非線性分數階KdV方程的研究目前還處于起步階段,已有方法主要有區域分解法[4]、同倫攝動法[5]、變分迭代法[6]等.
本文主要針對給定初值的時間分數階KdV方程,利用迭代法建立了在實空間內分數階KdV方程的級數解.在此基礎上首次考慮了復數域上的時間分數階復KdV方程,通過分解的方法將分數階復微分方程等價地轉化成實數域上相應的耦合系統,然后利用迭代法建立了分數階KdV方程在復數域上的級數解.
1 預備知識
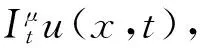
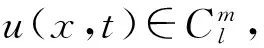
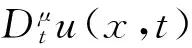

由上述定義可以得到以下性質:
2 迭代法
定理1 考慮非線性泛函方程
u(x,t)=f(x,t)+L(u(x,t))+N(u(x,t)),
(2)
其中f(x,t)是已知函數,L和N分別是定義在Banach空間B上的線性算子和非線性算子.假設方程(2)的解關于t是解析的,且算子L和N是壓縮的,那么方程(2)的解可以表示為
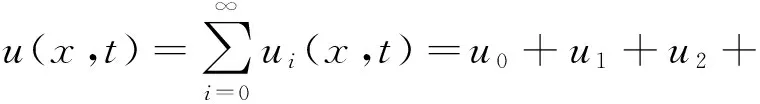
其中
u0=f,u1=L(u0)+N(u0),
um+1=L(um)+(N(u0+u1+…+um)-N(u0+u1+…+um-1)),m=1,2,….
證明 由假設可知方程的解可進行如下分解:
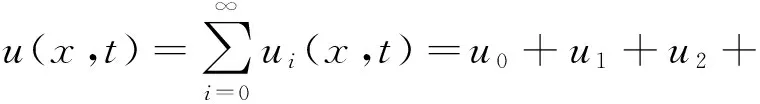
由于算子L是線性的,所以有
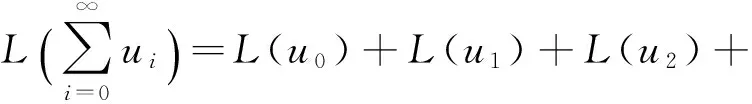
關于非線性算子N做如下分解:
從而方程(2)等價于
進一步得到
定義算子M:
M(u(x,t))=L(u(x,t))+N(u(x,t)).
定義迭代過程:
u0=f,u1=M(u0),
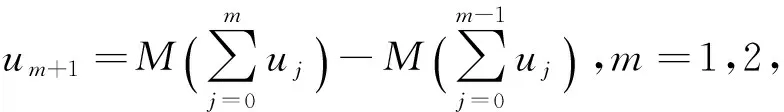
由于算子L和N是壓縮的,則M也是壓縮的,再根據文獻[7]中定理7,存在常數0 ‖M(vi)-M(vj)‖≤c‖vi-vj‖, 其中‖·‖定義為Banach空間的范數.進一步有 這里利用定理1的迭代法,分別給出時間分數階實KdV方程與復KdV方程的級數解. 3.1 時間分數階實KdV方程 考慮滿足一定初值條件的R上的時間分數階KdV方程 (3) 其中0<α≤1,u(x,t)∈R,(x,t)∈R×R. 假設u(x,t)關于t是解析的,那么u(x,t)可以表示為 1)_____Do all the risks have possible negative results? 再由初值 u0=ex, 從而由定理1迭代法有 進一步有 依次進行下去可得 所以方程(3)的級數解為 3.2 分數階復KdV方程 考慮時間分數階復KdV方程 (4) 其中0<α≤1,u(x,t)∈R,(x,t)∈R×R. 由于u是復函數,那么u可以寫成復數的一般形式 u=v1+iv2, 其中v1=v1(x,t),v2=v2(x,t)分別表示復數u的實部和虛部. 假設v1(x,t)和v2(x,t)關于t是解析的,那么v1(x,t)和v2(x,t)可改寫為 從而方程(4)等價于下面帶有初值條件的耦合方程組: (5) 再由初值 從而根據定理1迭代法有 f1(x,t)=ex,f2(x,t)=ex, 進一步有 依此進行下去,有 從而得到 u0=ex+iex, 所以方程(4)的級數解為 (6) 本文通過迭代法構造了分數階實(復)KdV方程初值問題的級數解,通過構造過程可以表明迭代法可以有效地構造分數階偏微分方程(組)初值問題的級數解. [1] 谷超豪,李大潛,沈瑋熙.應用偏微分方程[M].高等教育出版社,2014:38-186. [2] MILLER K S,ROSS B.An introduction to the fractional calculus and fractional differential equations [M].New York:Wiley,1993:8-146. [3] CAPUTO M.Linear models of dissipation whoseQis almost frequency independent:Ⅱ [J].J Roy Astr Soc,1967,13:529-539. [4] MOMANI S.An explicit and numerical solutions of the fractional KdV equation [J].Math Comput Simulation,2005,70(2):110-118. [5] WANG Q.Homotopy perturbation method for fractional KdV equation [J].Appl Math Comput,2007,190(2):1795-1802. [6] MOMANI S,ODIBAT Z,ALAWNEH A.Variational iteration method for solving the space-time-fractional KdV equation [J].Numer Methods Partial Differential Equations,2008,24(1):262-271. [7] XU F,GAO Y X,ZHANG W P.Construction of analytic solution for time-fractional boussinesq equation using iterative method [J/OL].Adv Math Phys,2015[2015-12-10].http://dx.doi.org/10.1155/2015/506140. (責任編輯:李亞軍) Series solutions of the time fractional KdV equations GAO Yi-xian,LI Jin-yu,XU Fei (School of Mathematics and Statistics,Northeast Normal University,Changchun 130024,China) The construction of series solution to the KdV equations in the sense of Riemann-Liouville integral and Caputo derivative is considered.For given initial value,by an iterative method,it can be successfully obtained the approximate series solutions of the real and complex KdV equations.By the construction process,it shows the iteration is an efficient method,which can be used to other fractional differential equations and even coupled systems. time fractional KdV equation;Riemann-Liouville integral;Caputo derivative;iterative method;series solution 1000-1832(2017)02-0001-05 10.16163/j.cnki.22-1123/n.2017.02.001 2015-12-10 國家自然科學基金資助項目(11471067);吉林省科技發展計劃資助項目(20160520094JH). 高憶先(1981—),男,博士,副教授,主要從事動力系統研究. O 193 [學科代碼] 110·51 A
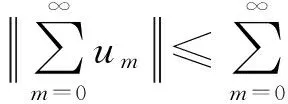

3 時間分數階KdV方程初值問題的級數解
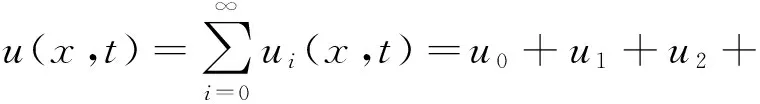
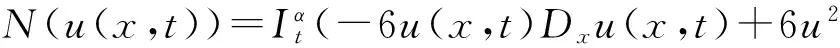
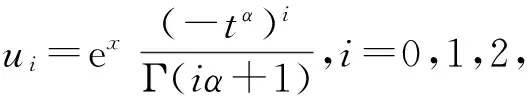
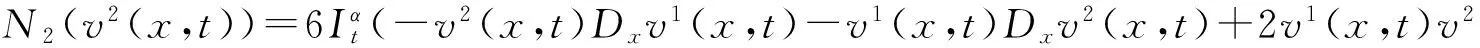
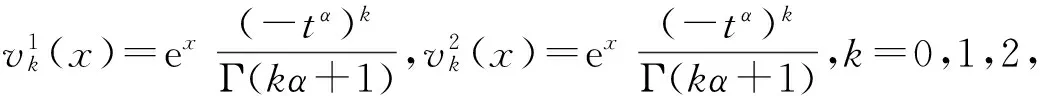
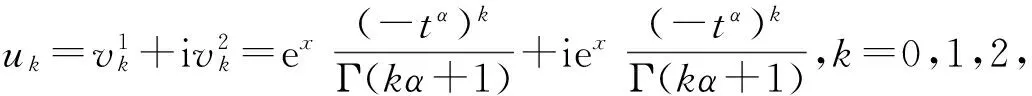
4 結論

