不同磁致伸縮方程下永磁電機的應力、應變研究

劉現偉，耿躍華

(河北工業大學，天津300130)

0 引 言

由于電機的振動噪聲不僅會影響環境質量而且還會使電機的使用壽命折損，因此電機中的振動噪聲一直是研究的熱點問題［1］。電機中的定子硅鋼片是一種磁導率很大的磁性材料，因此，當其處于變化的磁場下會出現沿磁場方向上的應力和由此引起的形變，由于上述情況的出現，就會導致電機定子出現整體的振動并產生噪聲。

電機振動噪聲的來源一般分為機械噪聲、空氣動力噪聲和電磁噪聲等［2］。以往認為電磁噪聲中的電磁力是其噪聲的主要來源，而隨著近些年的研究發現磁致伸縮效應對于電機的振動噪聲的影響也有著很大的比重。現階段磁致伸縮效應的應用大多都是磁致伸縮制動器、傳感器的方面，而關于磁致伸縮對電機噪聲影響研究還不太成熟［3］。2009 年，Sakda Somkun，Anthony J．Moses對磁致伸縮的各向異性和非取向電工鋼的機械特性進行了研究。通過測量研究發現磁致伸縮的各向異性對感應電機定子齒的非對稱形變有很大的影響［4］。韓雪巖等人也研究了理想電流和實驗電流供電下由電磁力和磁致伸縮效應單獨和共同作用下的電機振動［5］，實驗條件下得到的定子磁致伸縮位移大約為3．96×10－7m。2015年，沈陽工業大學的張艷麗，李強等人研究了諧波磁場下硅鋼片的磁致伸縮特性，得出了結論是諧波磁場下單片硅鋼片磁致伸縮引起的噪聲明顯增大［6］。因此研究磁致伸縮效應對電機振動噪聲的影響是有著重要的意義。

為了能準確地研究磁致伸縮效應對電機振動噪聲的影響，需要選取合適的方程來進行預測和分析。而應用不同的磁致伸縮本構方程對電機振動噪聲的預測分析結果也可能會有所不同。因此本文以單相永磁同步電機為例，研究了幾種本構方程對電機振動仿真結果的異同，對于永磁電機主要研究的是磁致伸縮效應對其定子硅鋼片的影響。

1 永磁電機的建模與分析

1． 1永磁電機模型

由于所研究的永磁同步電機的模型是軸對稱的，并且是可以旋轉拉伸的。因此在有限元軟件中可以對永磁同步電機由三維模型簡化為二維模型，從而可以減少計算量，節約計算時間。利用有限元軟件建立的二維永磁同步電機模型和研究中所使用的永磁同步電機相關的參數和參考點如圖1和表1所示。

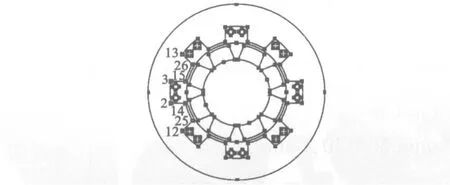
圖1 永磁電機模型及參考點

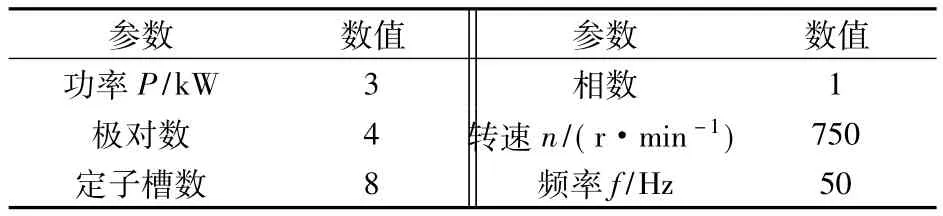
表1 電機主要參數

1． 2模型分析方法

模型分析采用有限元軟件COMSOL來實現的，通過軟件中的旋轉機械－磁與結構力學模塊進行耦合，實現電機中的磁－力耦合，得到由磁致伸縮效應引起的電機定子硅鋼片的應力與形變的結果。

磁－力耦合分析可以通過兩種形式來實現，一種是強耦合形式，通過直接對旋轉機械－磁和結構力學模塊相應的邊界條件和域的設置來直接耦合求解，得到相應的磁通密度、應力、形變等結果，一種是弱耦合形式，即先通過對旋轉機械－磁模塊的求解得到磁場的結果，再通過找到旋轉機械－磁與結構力學模塊之間的耦合關系來求解應力與應變。本文采用強耦合的形式來研究不同的磁致伸縮本構方程對永磁電機的振動噪聲的影響。

1． 3磁致伸縮本構方程

通過COMSOL軟件可以對二維電機模型進行有限元分析求解。應用軟件中的旋轉機械－磁與結構力學模塊對其進行強耦合求解。通過A－φ的方法(A是磁矢勢，φ是標量電位)求解電機內部的磁場分布及大小。然后由磁－力耦合得到由磁致伸縮效應引起的應力與形變。磁－力耦合是通過相應的磁致伸縮本構方程來實現的。

對電機硅鋼片有限元分析所使用的第一種磁致伸縮本構關系是基于線性壓磁方程描述的。方程是由應變和磁通密度方程組成。應變方程包括由應力和外加磁場共同作用時引起的應變。磁通密度方程是由應力和外加磁場產生的磁通密度［7］。當只考慮單一方向上的磁致伸縮時方程可表示:

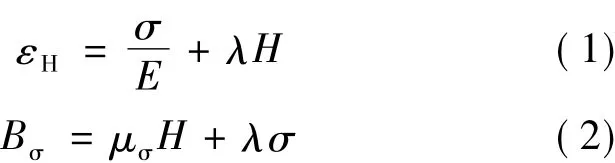
式中:εH為硅鋼片在磁場強度為H時的總應變;E為楊氏模量;σ為應力;λ為磁致伸縮系數;H為磁場強度;Bσ為應力作用下的磁感應強度;μσ為應力作用下的磁導率。

對于二維彈性材料而言，應力與應變之間的關系式為σ=Dε，其中D為剛度矩陣，剛度矩陣表達式:

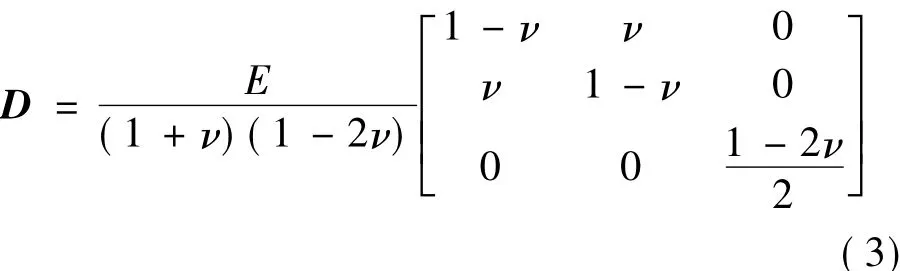
隨著對磁性材料中磁致伸縮效應研究的廣泛深入，研究者們所提出的磁致伸縮本構關系也不僅限一種。假定定子硅鋼片中的磁致伸縮效應是各向同性的，并用等效節點力來模擬磁致伸縮力。利用有限元分析方法對電機進行單元剖分，則每個單元節點在磁場的作用下，由于磁致伸縮效應在節點處產生磁致伸縮力。當定子硅鋼片受到磁場的作用時，由于磁致伸縮效應產生的應變是由平行于磁場方向和垂直于磁場方向上的應變組成，此時應力與應變的之間關系應用的是胡克定律，其表達式如下［8］:

式中:σ為應力;α為材料常數;ε為應變;εP為平行于磁場方向上的應變變;εv為垂直于磁場方向上的應變;ν為泊松比;E為楊氏模量。

假設在剖分單元ie上的等效節點ip上磁致伸縮力和位移分別為fip和uip。在單元上的節點的ip位移示意圖如圖2所示。則在單元節點上的位移和

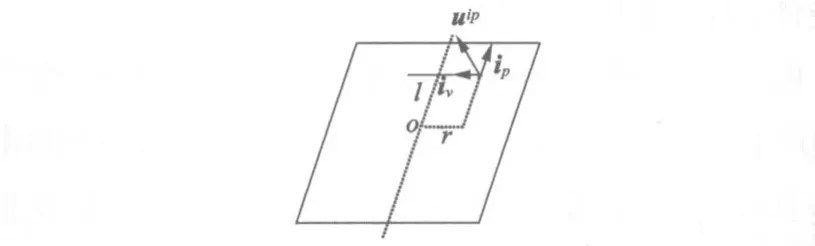
圖2 等效節點位移示意圖

磁致伸縮力:

式中:K為剛度矩陣，iv為垂直于磁場強度的單位矢量，ip為平行于磁場強度的單位矢量。

第三種磁致伸縮本構方程是從硅鋼片被磁化的角度來研究。在二維電機中主要研究電機定子齒徑向和垂直于徑向方向上的磁致伸縮。它在任意方向的磁致伸縮量的表達式如下［9］:

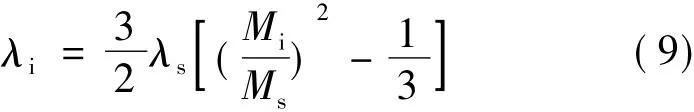
式中:λi為i方向上的磁致伸縮量;λs為磁致伸縮常數;Mi為i方向上磁性材料的磁化強度;Ms為磁性材料的飽和磁化強度項表明當沒有任何磁場存在的情況，磁性材料中的磁矩是隨機取向的。當假設的材料有足夠的預應力，使得所有的磁矩都垂直于磁化過程開始時的磁場方向時可以將式(9)中的忽略掉，從而簡化為下式:

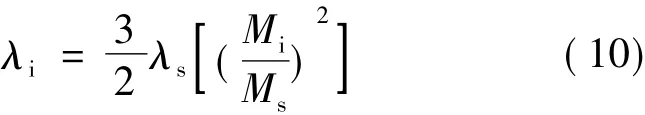
應用以上3種不同的磁致伸縮本構方程來仿真永磁電機在變化的磁場作用下，定子硅鋼片受磁致伸縮效應影響的磁通密度、應力和應變。在電機圖中分別選取定子齒根部、齒頂部的幾個點來研究相關參量。通過比較這3種本構方程作用下的結果，得出幾種不同本構方程的異同和對結果產生的影響。

2 結果分析

應用3種本構關系方程式對永磁電機仿真得到的0．01 s時的磁通密度結果分布圖和采樣點13在0～0．005 s處的3種本構關系下參考點的磁通密度B1，B2，B3分別如圖3和表2所示。

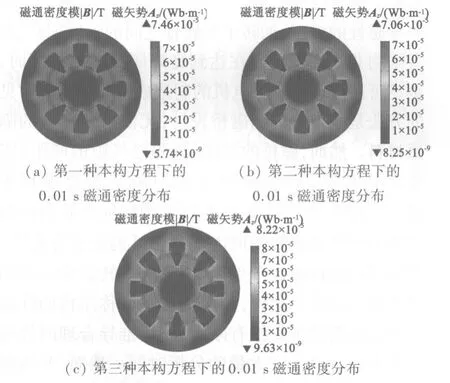
圖3 永磁同步電機磁通密度分布圖

應力在0～0．01 s之間的磁致伸縮力密度均值如表3所示。

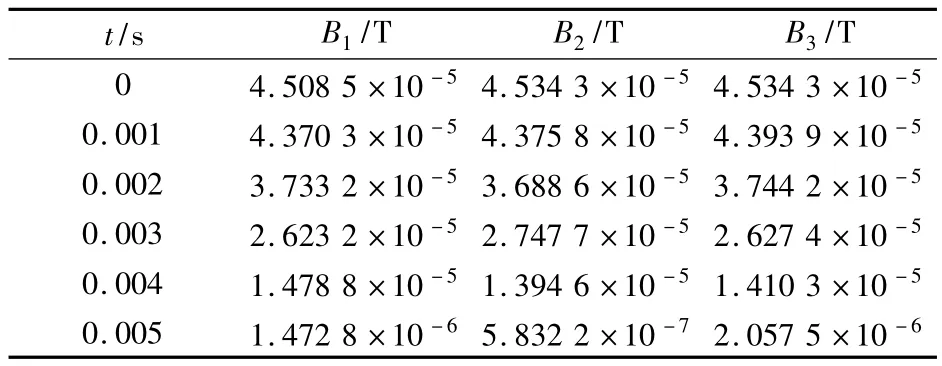
表2 采樣處0～0．005 s時的磁通密度

表3 樣點磁致伸縮力密度均值

通過對比3種本構關系下的磁通密度圖和采樣處0～0．01 s時的磁通密度值表明:應用3種不同的磁致伸縮本構關系仿真得出的電機的內部磁通密度的分布及大小并無太大的差別。同時也可以直觀地看到在電機中磁通密度模值較大的部分是定子硅鋼片的定子齒部。因此磁致伸縮效應引起的應力較大的分布位置主要是在定子齒根部、齒頂部的部位。

另外，通過仿真還得到了8個參考點處隨時間變化的磁致伸縮力密度時域圖，以及樣點13處0～0．02 s之間的位移數值大小。由此可以了解電機磁致伸縮力隨時間變化的大小、規律和位移大小。應用3種本構關系仿真得到的磁致伸縮力密度隨時間變化的時域圖和位移數值如圖4、表4所示。

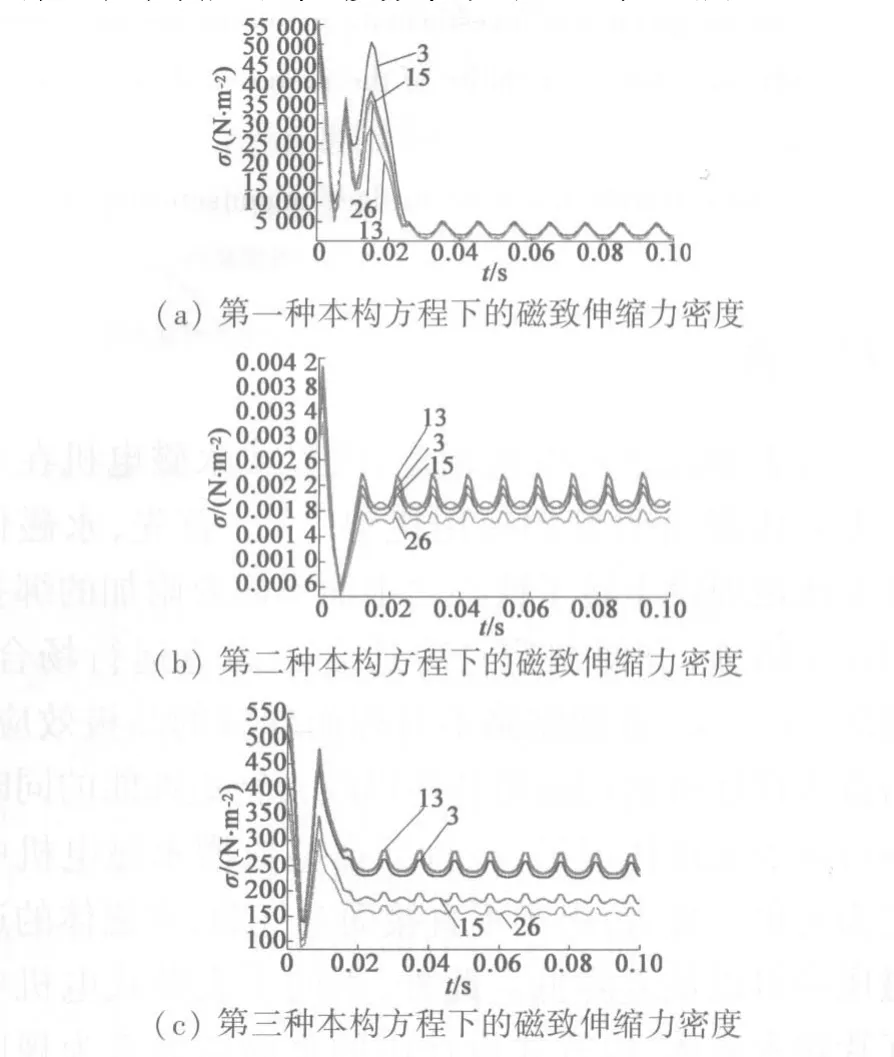
圖4 永磁同步電機磁致伸縮力密度

表4 樣點13 3種本構方程下的位移數值

通過對應力密度均值的對比分析可知，電機定子硅鋼片在磁場的作用下定子齒根部的應力模值要大于齒頂部的應力模值，因此由磁致伸縮效應引起的應力會導致電機定子硅鋼片的振動和形變。了解磁致伸縮效應對電機產生的應力，并由此引起的振動對解決電機中振動噪聲問題提供了研究的方向。

通過數據比較得出：應用不同的磁致伸縮本構方程仿真得出的應力的變化頻率隨時間基本成周期性變化關系，而且變化的頻率約為供電頻率的2倍關系，且在大約100 Hz處達到最大值。并且，3種本構方程下的電機應力和位移數值大小卻有著數量級的差異。經對比分析發現，利用線性壓磁方程得到的振動位移數據與從磁化角度得到的數據較為接近。

3 結 語

應用不同磁致伸縮本構方程仿真得到的電機磁通密度的大小及分布大體上是相同的，而且都表現出來的是在定子的齒根部和齒頂部磁通密度比較大。

結果表明，永磁電機受磁致伸縮效應影響產生的應力和應變主要是定子齒根部和齒頂部較大。而且應力的變化的頻率是電機供電頻率的2倍。且齒根部的應力模值大于齒頂部應力模值。3種方程所得出的磁通密度的模值及分布無明顯差別，而應力、位移的模值卻有著數量級的差異。且線性壓磁方程下得到的數據與先前研究者們實驗條件下得到的磁致伸縮數據更為接近，考慮電磁－機械之間的相互耦合使預測的結果更接近于實際。通過對不同本構方程的研究為預估分析電機中由磁致伸縮效應引起的應力、應變等提供了合適的耦合方程與方法。

［1］ 祝麗花，楊慶新，閆榮格，等．考慮磁致伸縮效應電力變壓器振動噪聲的研究［J］．電工技術學報，2013，28（4）：1－7．

［2］ 劉鳴，景建方．降低電機噪聲的方法研究［J］．船電技術，2011，31（12）：21－24．

［3］ BELA HCEN A ．Vibr ation of r otating electrical machines due to magnetomechanical coupling and magnetostriction ［J］．IEEE Tr ansactions on Magnetics，2006，42（4）：971－974．

［4］ SOMKUN S，Anthony J．Moses，Philip I．Anderson．Ef f ect of magnetostriction anisotr opy in Nonoriented electrical steels on def or mation of Induction motor stator cores［J］．IEEE Tr ansactions on Magnetics，2009，45（10）：4744－4747．

［5］ 韓雪巖，張哲，吳勝男，陳健．考慮磁致伸縮效應永磁電機的振動噪聲研究［J］．電工電能新技術，2015，34（1）：28－34．

［6］ 張艷麗，李強，王洋洋，等．諧波磁場下硅鋼片磁致伸縮特性分析［J］．電工技術學報，2015，30（14）：544－549．

［7］ 張艷麗，孫小光，謝德馨，等．無取向電工鋼片磁致伸縮特性測量與模擬［J］．電工技術學報，2013，28（11）：176－182．

［8］ GAO Yanhui，MURA MATSU K，et al．Vibr ation anal ysis of a reactor driven by an inverter power suppl y considering electro magnetism and magnetostriction ［J］．IEEE Tr ansactions on magnetics，2009，45（10）：4789－4792．

［9］ ZHANG Xin，YANG Qingxin，ZHANG Xian．Nu merical anal ysis of stress in the l ar ge per manent magnet motor stator cores incl uding magnetostriction ef f ects［J］．Inf or mation Technology Jour nal，2013，12（12）：8235－8241．