基于加權矢量場的軌跡層次聚類*

陳 琳， 王 蒙

(昆明理工大學 信息工程與自動化學院，云南 昆明 650500)

基于加權矢量場的軌跡層次聚類*

陳 琳， 王 蒙

(昆明理工大學 信息工程與自動化學院，云南 昆明 650500)

傳統的軌跡聚類方法存在定義軌跡相似度難度大，聚類過程中容易忽略軌跡細節等問題。基于矢量場的軌跡聚類(VFC)在保持軌跡原始運動特征的基礎上，利用矢量場的幾何結構可以很好地度量軌跡相似度。引入加權擬合方法，降低噪聲對聚類的影響，以解決VFC魯棒性較差問題。采用層次聚類動態地決定聚類類別數，以解決聚類類別數不能自適應的問題，提高聚類有效性。采用亞特蘭大颶風數據作為實驗原始軌跡數據，分別使用經典矢量場的軌跡聚類，k-means聚類，k-mediods聚類以及提出的方法進行實驗，實驗結果證明了加權擬合矢量場的層次聚類算法的有效性。

軌跡； 矢量場聚類； 加權擬合； 層次聚類

0 引 言

軌跡是對一個移動對象位置和時間的記錄序列。作為一種重要的時空對象數據類型和信息源，軌跡的應用范圍涵蓋了人類行為、交通物流、應急疏散管理和動物習性等諸多方面。生態學家通過學習動物的運動，來獲取動物種群的增長，遷徙模式[1]。氣象學家通過軌跡數據來幫助預測風暴的路徑[2]。

目前，軌跡聚類的方法主要包括兩類，一類是將軌跡嵌入到一個度量空間中，定義軌跡的相似度概念，使用基于軌跡點的聚類。Lee J G等人[3]提出關于軌跡聚類的新的分割與群組的框架，將一條軌跡劃分成不同的段，然后將相似的段聚到一類中。Gudmundsson J等人[4]將多個領域的軌跡數據嵌入運動空間進行概念建模,該方法的缺點是，定義軌跡相似度難度大，容易忽略軌跡中細節的部分。另一類是基于模型的方法,Wei J等人[5]擴展和并行化回歸模型對大量軌跡進行聚類。Gaffney S J等人[6]采用曲線混合模型對經緯度空間的冬季溫帶氣旋進行概率聚類。這種方法模型適應性不強，軌跡數據不同需要的聚類模型不同。

基于矢量場軌跡聚類(VFC)方法，可以有效地解決上述定義軌跡相似度難度大，容易忽略軌跡中細節部分和算法適應性不強等問題。VFC算法利用軌跡的幾何結構來自動編碼軌跡特征，從而度量軌跡相似度，很好地保留軌跡原有特征。Ferreira N等人[7]通過VFC算法，研究臺風運動與GPS行人追蹤等。Brillinger D R等人[8]利用VFC算法研究動物的運動規律。Camargo S J[9]利用VFC算法研究臺風的活動規律。文獻[7～9]存在聚類類別不能自適應，沒有考慮采集軌跡過程中的量測噪聲，算法魯棒性差等問題。

針對上述VFC算法中聚類類別數不能自適應的問題，本文提出了層次聚類的方法。將矢量場作為聚類依據，通過設置閾值使算法自動對軌跡進行分類。針對算法魯棒性差，易受噪聲干擾的問題，提出加權擬合矢量場的方法。給噪聲數據分配較小的權重，減小噪聲數據對矢量場擬合的影響。通過實驗對基于加權矢量場的軌跡層次聚類(WVFHC)進行驗證，效果較好。

1 基于加權矢量場的軌跡層次聚類算法

1.1 數據預處理

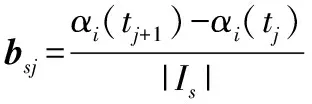
點bsj(x,y)為軌跡Ti上一坐標點，點Q11(x11,y11),Q12(x12,y12),Q21(x21,y21),Q22(x22,y22)為bsj(x，y)周圍最近的4個坐標點如圖1(a)。定義dx=x-[x],dy=y-[y]，則點Q11(x11,y11)，Q12(x12,y12)，Q21(x21,y21)，Q22(x22,y22)可以通過bsj(x,y)表示

Q11(x11,y11)=bsj(x,y)·dx·(1-dy)

(1)

Q21(x21,y21)=bsj(x,y)·dx·dy

(2)

Q22(x22,y22)=bsj(x,y)·(1-dx)·dy

(3)

Q12(x12,y12)=bsj(x,y)·(1-dx)·(1-dy)

(4)

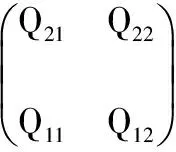
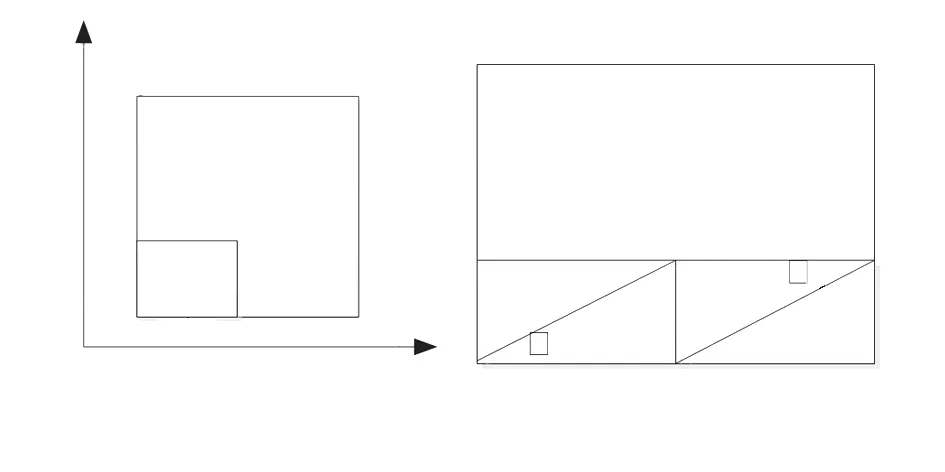
圖1 雙線性插值和拉普拉斯貝特拉米算子

1.2 軌跡數據矢量場擬合

假設對于一組軌跡數據α={T1,T2,…,Tn}存在一組平滑的矢量場Xj來解釋這組軌跡中的移動規律,即需要找到矢量場Xj與類別集合Φ∶α→{1,2,…,k}來解釋該組軌跡的移動規律。

如圖1(b)所示采用拉普拉斯貝特拉米算子L作為平滑矩陣對矢量場進行平滑

(5)

則該組軌跡的移動規律可以表示為

(6)

式中L為拉普拉斯余切矩陣；Xj為擬合之后的矢量場。

用矩陣的形式表示并進行最小二乘擬合，定義能量函數E，則式(6)可化簡為求E=‖LX‖2+‖CX-b‖2的最小值,其中，C為網格數據，b為原始軌跡數據。

1.3 軌跡數據加權矢量場擬合

在軌跡數據采集過程中設備誤差可能會生成存在噪聲的軌跡數據，若直接運算，可能對聚類結果產生影響,進行加權擬合，會降低噪聲對聚類結果的影響。加權矢量場擬合的核心部分為權值的確定，權值通過調諧常數cH與局部估計噪聲偏差σ共同確定[10，11]。其中

σ=1.482 6 med|ri-medri|

(7)

式中 ri為第i個數據點的殘差。

(8)

式中cH為調諧常數，取固定值1.345;wH,i為權重矩陣。

通過迭代更新權值矩陣wH,i，定義停止準則F(l)來停止迭代過程

(9)

式中l為當前迭代過程。當第l次迭代過程與第l-1次迭代過程的差值小于0.001時，迭代收斂，即

|F(l)-F(l-1)|<0.001，l=1,2,…

(10)

對能量函數E中的擬合部分進行加權,即

E=‖LX‖2+‖W(CX-b)‖2

(11)

X=(LTL+CTWTWC)CTWTWb

(12)

式中W為權重矩陣。

1.4 矢量場層次聚類

VFC算法聚類類別數需提前設定，適應性較差。使用層次聚類，通過設置閾值動態地決定聚類類別數，提高算法的適應性。

WVFHC算法步驟如下：

1)輸入：軌跡數據α={T1,T2,…,Tn},th;

2)初始化：根據1.1節將軌跡數據映射到網格Ci上，i=1;

3)根據式(12)由Ci得到Xi;

4)i=i+1;

5)若i

6)采用層次聚類方法，根據聚類閾值th對V聚類得到M類，Φj={Φj,j=1,2,3,…,M}(M不固定)，且{Xi,i∈Φj};

7)分別輸出聚類后的矢量場Yj。

2 實驗結果與分析

2.1 實驗設計與評價指標

用文獻[7]中的颶風數據以及人造數據作為實驗數據。用颶風數據進行了VFC算法，k-means[12～14]算法，k-medoids[15]算法以及VFHC算法實驗。用人造數據進行了VFHC算法與WVFHC算法實驗。

采用4種性能評價指標[16]：RS(R-Squares)[17，18],CH指數(Calinski-Harabaszindex)[19],DB指數(Davies-Bouldinindex)[20]與修正的HubertГ統計(ModifiedHubertΓstatistic)[21]。QCH，QRS，QГ值越高聚類結果越準確,QDB值越小聚類結果越準確。

2.2 實驗結果與分析

2.2.1 真實數據集

利用文獻[7]中的颶風數據作為真實數據集，包含1 415條軌跡。

設置不同的閾值，得到不同的聚類類別數，結果如表1所示,NC為聚類類別數。圖2(a)～(d)為評價指標折線圖，可以看出:在閾值為“1.5”時，QDB發生異常變化，其他指標沒有出現異常，所以閾值為“2.5”，“2”與“1.8”時，聚類效果較好，對應的類別數分別為“4”，“5”與“6”。

圖2(e)～(h)為4種算法評價指標直方圖，可以看出:在聚類類別數為“4”，“5”，“6”時。VFHC算法的聚類效果更好。因為在聚類類別數較小時，k-means算法,k-medoids算法與VFC算法固定了聚類類別數，使每一類中的軌跡數據方差變大，所以聚類效果較差。VFHC算法通過閾值獲取聚類類別，每一類中的軌跡數據相似度更高，所以聚類效果更好。圖4為VFHC算法在閾值為2.5時各類別的矢量場圖。

圖2 實驗結果

圖3 實驗數據

圖4 閾值為2.5時各類的矢量場圖

閾值評價指標QCHQDBQRSQГ2．5(NC=4)7．64×1050．00280．0888851．97782(NC=5)9．54×1050．00170．010971．90081．8(NC=6)1．18×1060．03180．16595．81991．5(NC=7)1．35×106183．50470．21123．18881．3(NC=9)1．57×106108．77830．2102183．1176

2.2.2 人造數據集

從颶風數據中隨機選取142條軌跡，加入噪聲得到人造數據集。原始軌跡數據與噪聲軌跡數據如圖3(b)，圖3(c)所示。將人造數據替換原來的軌跡數據作為人造數據集。采用加權擬合與不加權擬合得到矢量場，進行層次聚類。

圖2(i)～(l)為評價指標直方圖，可以看出，WVFHC算法的聚類效果好。因為加入噪聲后，VFHC算法將異常數據作為正常數據進行矢量場擬合，影響聚類結果。而WVFHC算法通過給異常數據分配較小的權重，降低異常數據的影響，所以聚類效果較好。

3 結 論

本文提出WVFHC方法，對真實軌跡數據與人造軌跡數據進行聚類。VFHC方法能夠解決VFC算法聚類類別數不能自適應的問題。通過與k-means算法，k-medoids算法，VFC算法的實驗對比得出，在聚類類別較小時效果較好，但在聚類類別較大時效果較差。通過WVFHC方法對人造軌跡數據進行聚類，能夠降低噪聲的干擾，增強算法的魯棒性。通過與VFHC算法的對比得出，WVFHC算法效果更好。在今后的研究中，研究重點為改進WVFHC算法，增強算法的適應性。

[1] Grundy E,Jones M W,Laramee R S,et al.Visualisation of sensor data from animal movement[J].Computer Graphics Forum,2009,28(3):815-822.

[2] Camargo S J,Robertson A W,Gaffney S J,et al.Cluster analysis of typhoon tracks[J].Journal of Climate,2007,20(14):3654-3676.

[3] Lee J G,Han J,Whang K Y.Trajectory clustering:A partition-and-group framework[C]∥Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data,ACM,2007:593-604.

[4] Gudmundsson J,Laube P,Wolle T.Computational movement analysis[M].Berlin Heidelberg：Springer,2012:423-438.

[5] Wei J,Wang C,Yu H,et al.A sketch-based interface for classi-fying and visualizing vector fields[C]∥2010 IEEE Pacific Visua-lization (PacificVis)Symposium,IEEE,2010:129-136.

[6] Gaffney S,Smyth P.Trajectory clustering with mixtures of regression models[C]∥Proceedings of the Fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,ACM,1999:63-72.

[7] Ferreira N,Klosowski J T,Scheidegger C E,et al.Vector fieldk-means:Clustering trajectories by fitting multiple vector field-s[C]∥Computer Graphics Forum,2013:201-210.

[8] Brillinger D R,Preisler H K,Ager A A,et al.An exploratory data analysis(EDA)of the paths of moving animals[J].Journal of Statistical Planning and Inference,2004,122(1):43-63.

[9] Camargo S J,Robertson A W,Gaffney S J,et al.Cluster analysis of typhoon tracks—Part II:Large-scale circulation and ENSO[J].Journal of Climate,2007,20(14):3654-3676.

[10] Meer P,Mintz D,Rosenfeld A,et al.Robust regression methods for computer vision:A review[J].International Journal of Computer Vision,1991,6(1):59-70.

[11] 嚴筱永,錢煥延,施衛娟,等.一種利用統計中值的加權定位算法[J].傳感器與微系統,2011,30(8):120-123.

[12] MacQueen J B.On the asymptotic behavior ofk-means[R].Los Angeles:Western Management Science Inst,Univ of California at Los Angeles,1965.

[13] 王聯國,韓曉慧,宋 磊.基于改進混合蛙跳-K均值聚類算法的無功電壓控制分區[J].傳感器與微系統,2013,32(6):18-21.

[14] 張乙竹,周禮爭,唐 瑞,等.基于k-means聚類點密度的WSNs加權質心定位算法[J].傳感器與微系統,2015,34(7):125-127.

[15] Kaufman L,Rousseeuw P.Clustering by means of medoids[M].Amsterdam:North-Holland Publisher,1987.

[16] Liu Y,Li Z,Xiong H,et al.Understanding of internal clustering validation measures[C]∥2010 IEEE 10th International Confe-rence on Data Mining(ICDM),IEEE,2010:911-916.

[17] Sharma S.Applied multivariate techniques[M].New York:John Wiley & Sons Inc,1995.

[18] Halkidi M,Batistakis Y,Vazirgiannis M.On clustering validation techniques[J].Journal of Intelligent Information Systems,2001,17(2):107-145.

[19] Caliński T,Harabasz J.A dendrite method for cluster analy-sis[J].Communications in Statistics-theory and Methods,1974,3(1):1-27.

[20] Davies D L,Bouldin D W.A cluster separation measure[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1979(2):224-227.

[21] Hubert L,Arabie P.Comparing partitions[J].Journal of classification,1985,2(1):193-218.

王 蒙(1985-)，博士，講師，主要從事計算機視覺、圖像處理、機器學習，以及語音識別方向研究工作,E—amil:vicong@live.com。

Trajectory hierarchical clustering based on weighted vector field*

CHEN Lin, WANG Meng

(School of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China)

It is hard to define similarity of trajectories and trends to ignore details of trajectories using a traditional trajectory clustering method.Vector field based clustering methods keep the inherent features of movements and measures similarities of trajectories with the geometric structure information derived from it.Weighted fitting scheme is introduced to weaken the effects of noises and increase the robustness of clustering.A hierarchical approach is employed to automatically determine the number of class solving the problem that traditional methods cannot be self-adaptive to clustering,thus improving the effectiveness of our method.Experiments of traditional vector field clustering,k-means clustering andk-mediods clustering as well as the proposed method are conducted on the Atlanta Hurricane dataset,and the result shows the effectiveness of the hierarchical clustering algorithm based on weighted vector field.

trajectory; vector field clustering; weighted fitting; hierarchical clustering

2016—06—08

國家自然科學基金地區基金資助項目(61563025)；云南省教育廳科學研究基金資助項目(2015Z047)

10.13873/J.1000—9787(2017)06—0010—04

TP 311

A

1000—9787(2017)06—0010—04

陳 琳(1992-)，男，碩士研究生，主要研究方向為計算機視覺、模式識別。